Уклон 1 2: 2. Уклоны и конусность – 2.1.2.Построение уклона и конусности

2.1.2.Построение уклона и конусности

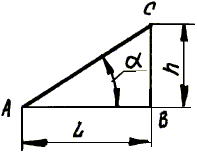
Уклон – это величина, которая характеризует наклон одной линии по отношению к другой. Уклон i прямой АС относительно прямой АВ (рис. 37) определяется как отношение разности высот двух точек А и С к горизонтальному расстоянию между ними:

Уклон может быть выражен простой дробью, десятичной или в процентах.

Рис. 37. Уклон прямой

Рис. 38. Построение прямой с уклоном 1:5

Задача. Через точку А провести прямую АС с уклоном 1:5 к горизонтальной прямой (рис. 38). Из точки А проводят горизонтальный луч и откладывают на нем пять произвольных равных отрезков. На перпендикуляре, восстановленном из конечной точки В, откладывают одну такую часть. Уклон гипотенузы АС треугольника АСВ будет равен 1:5.

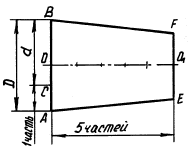
Конусность К определяется как отношение разности диаметров D и d двух поперечных сечений конуса к расстоянию между ними (рис. 39).

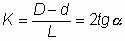
Рис. 39. Конусность

Рис. 40. Построение конусности 1:5

Конусность, как и уклон, выражается простой дробью, десятичной или в процентах. На рис. 40 показано построение конусности 1:5. ВС=FЕ.

2.1.3. Лекальные кривые. Построение эллипса и эвольвенты

Очертания многих элементов деталей в машиностроении, в строительных конструкциях и различных инженерных сооружениях имеют кривые линии. Кривые, графическое построение которых производят циркулем, называются циркульными кривыми (окружности, коробовые кривые, завитки). Кривые, графическое построение которых выполняется с помощью лекал, называются лекальными кривыми (эллипс, парабола, гипербола и т.д.).

Эллипсом называется геометрическое место точек М плоскости, сумма расстояний которых от двух данных точек F₁ и F₂ есть величина постоянная и равна отрезку АВ (рис. 41,а).

Точки F₁ и F₂ называются фокусами эллипса; отрезок АВ — большой осью; отрезок СD, перпендикулярный к АВ – малой осью; точка О – центром эллипса. Каждой точке эллипса соответствуют две точки, расположенные симметрично относительно большой и малой осей, и одна точка, расположенная симметрично относительно центра эллипса О. На рис. 42,б, а точки, симметричные М, обозначены М₁, М₂ и М₃.

Рис. 41. Эллипс

Прямая, проходящая через центр эллипса, называется его диаметром. Большая и малая оси называются главными диаметрами эллипса. Два диаметра эллипса называются сопряженными, если каждый из них делит пополам хорды, параллельные другому диаметру.

Рассмотрим один из способов построения эллипса по большой АВ и малой СD осям (рис. 41, а, б):

1). Из центра О проводим вспомогательные окружности диаметрами соответственно равным величине большой оси эллипса АВ и малой СD.

2). Для построения любой точки J эллипса (рис. 42,а) из центра О проводим любую секущую прямую и отмечаем точки i и i₁ пересечения ее со вспомогательными окружностями.

3). Из точки i на большой окружности проводим прямую, перпендикулярную большой оси АВ, через точку i₁ – прямую, перпендикулярную малой оси СD. Точка J пересечения этих прямых является искомой точкой эллипса. Помня о свойстве симметрии эллипса, определяем J₁, J₂ и J₃.

В практической работе (рис.42,б) секущие прямые проводят через точки деления большой окружности на 12 и более равных частей.

 

Рис. 42. Построение эллипса по большой АВ и малой СD осям.

Эвольвента— плоская кривая, образуемая траекторией любой точки прямой линии, перекатываемой по окружности без скольжения.

Рассмотрим способ построения эвольвенты окружности (рис.43):

1). Из конечной точки вертикального диаметра А(самая нижняя точка окружности) проводят касательную, на которой откладывают длину окружности (πD). Этот отрезок и окружность делят на одинаковое количество частей (например, 12).

2). В точках 1, 2, 3…11на окружности проводят касательные к ней, на которых соответственно откладывают отрезкиА1₁

, А2₁, А3₁…А11₁.

3). Полученные точки 1’…12’будут принадлежать очерку эвольвенты окружности. Соединяют эти точки при помощи гладкой лекальной кривой.

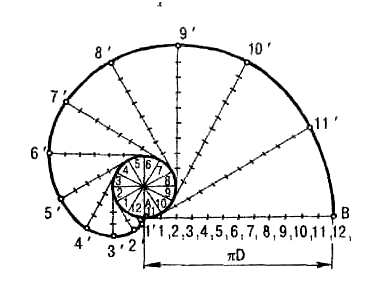
Рис.43. Эвольвента окружности.

2.1.2. Построение уклона и конусности

Уклон – это величина, которая характеризует наклон одной линии по отношению к другой. Уклон i прямой АС относительно прямой АВ (рис. 37) определяется как отношение разности высот двух точек А и С к горизонтальному расстоянию между ними:

Уклон может быть выражен простой дробью, десятичной или в процентах.

Рис. 37. Уклон прямой

Рис. 38. Построение прямой с уклоном 1:5

Задача. Через точку А провести прямую АС с уклоном 1:5 к горизонтальной прямой (рис. 38). Из точки А проводят горизонтальный луч и откладывают на нем пять произвольных равных отрезков. На перпендикуляре, восстановленном из конечной точки В, откладывают одну такую часть. Уклон гипотенузы АС треугольника АСВ будет равен 1:5.

Конусность К определяется как отношение разности диаметров D и d двух поперечных сечений конуса к расстоянию между ними (рис. 39).

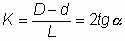
Рис. 39. Конусность

Рис. 40. Построение конусности 1:5

Конусность, как и уклон, выражается простой дробью, десятичной или в процентах. На рис. 40 показано построение конусности 1:5. ВС=FЕ.

2.1.3. Лекальные кривые. Построение эллипса и эвольвенты

Очертания многих элементов деталей в машиностроении, в строительных конструкциях и различных инженерных сооружениях имеют кривые линии. Кривые, графическое построение которых производят циркулем, называются циркульными кривыми (окружности, коробовые кривые, завитки). Кривые, графическое построение которых выполняется с помощью лекал, называются лекальными кривыми (эллипс, парабола, гипербола и т.д.).

Эллипсом называется геометрическое место точек М плоскости, сумма расстояний которых от двух данных точек F₁ и F₂ есть величина постоянная и равна отрезку АВ (рис. 41,а).

Точки F₁ и F

2 называются фокусами эллипса; отрезок АВ — большой осью; отрезок СD, перпендикулярный к АВ – малой осью; точка О – центром эллипса. Каждой точке эллипса соответствуют две точки, расположенные симметрично относительно большой и малой осей, и одна точка, расположенная симметрично относительно центра эллипса О. На рис. 42,б, а точки, симметричные М, обозначены М₁, М₂ и М₃.

Рис. 41. Эллипс

Прямая, проходящая через центр эллипса, называется его диаметром. Большая и малая оси называются главными диаметрами эллипса. Два диаметра эллипса называются сопряженными, если каждый из них делит пополам хорды, параллельные другому диаметру.

Рассмотрим один из способов построения эллипса по большой АВ и малой СD осям (рис. 41, а, б):

1). Из центра О проводим вспомогательные окружности диаметрами соответственно равным величине большой оси эллипса АВ и малой СD.

2). Для построения любой точки J эллипса (рис. 42,а) из центра О проводим любую секущую прямую и отмечаем точки i и i₁ пересечения ее со вспомогательными окружностями.

3). Из точки i на большой окружности проводим прямую, перпендикулярную большой оси АВ, через точку i₁ – прямую, перпендикулярную малой оси СD. Точка J пересечения этих прямых является искомой точкой эллипса. Помня о свойстве симметрии эллипса, определяем J₁, J₂ и J₃.

В практической работе (рис.42,б) секущие прямые проводят через точки деления большой окружности на 12 и более равных частей.

 

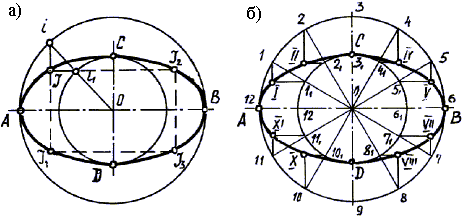
Рис. 42. Построение эллипса по большой АВ и малой СD осям.

Эвольвента — плоская кривая, образуемая траекторией любой точки прямой линии, перекатываемой по окружности без скольжения.

Рассмотрим способ построения эвольвенты окружности (рис.43):

1). Из конечной точки вертикального диаметра А (самая нижняя точка окружности) проводят касательную, на которой откладывают длину окружности (πD). Этот отрезок и окружность делят на одинаковое количество частей (например, 12).

2). В точках 1, 2, 3…11 на окружности проводят касательные к ней, на которых соответственно откладывают отрезки А1₁, А2₁, А3₁…А11₁.

3). Полученные точки

1’…12’ будут принадлежать очерку эвольвенты окружности. Соединяют эти точки при помощи гладкой лекальной кривой.

Рис.43. Эвольвента окружности.

5.3 уклон, конусность, сопряжения

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ»

Утверждено на заседании кафедры начертательной геометрии и черчения

21 июня 2011г.

ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ –

УКЛОНЫ, КОНУСНОСТЬ, СОПРЯЖЕНИЯ

Методические указания для всех специальностей

Квалификация выпуска «Бакалавр»

Ростов-на-Дону

2011

2

Геометрические построения – уклоны, конусность, сопряжения:

Методические указания для всех специальностей. — Ростов н/Д: Рост. гос.

строит. ун-т, 2011. – 8с.

Содержат геометрические построения, необходимые для выполнения задания по инженерной графике.

Составитель: ассист. А.В. Федорова

Редактор Н.Е. Гладких Темплан 2011 г., поз. 137.

____________________________________________________________________

Подписано в печать 6.07.11. Формат 60х84/16.

Бумага писчая. Ризограф. Уч.-изд.л. 0,3. Тираж 20 экз. Заказ 341.

____________________________________________________________________

Редакционно – издательский центр Ростовского государственного строительного университета.

344022, Ростов – на – Дону, ул. Социалистическая, 162

Ростовский государственный строительный университет, 2011

3

ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ – УКЛОНЫ, КОНУСНОСТЬ,

СОПРЯЖЕНИЯ

При изготовлении профилей прокатной стали, боковые полки выполняют так, что плоскости, ограничивающие их, не параллельны, а расположены под некоторым углом между собой.

В технике часто применяются конические детали. При вычерчивании чертежей многих деталей приходится выполнять ряд геометрических построений, и в этой связи рассмотрим следующие понятия: уклоны, конусность, сопряжения.

УКЛОНЫ

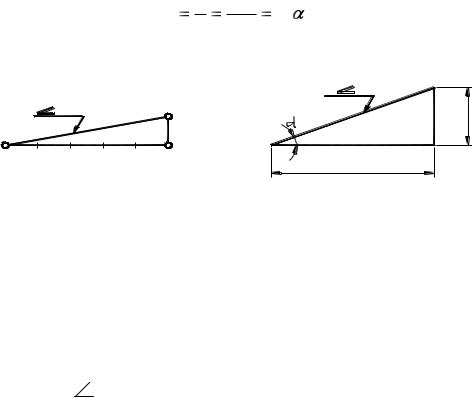
Уклон – наклон одной прямой линии к другой (рис.1).

Уклон i прямой АС определяется из прямоугольного треугольника АВС как отношение противолежащего катета ВС к прилежащему катету АС (рис.2):

	i	h	BC	tg .
		l	AC
				i	В
1:5	В				h
А	1 С			А	С
5 4 3 2
				l
Рис.1				Рис.2

Уклон может быть выражен в процентах (например, уклон в 10%

внутренних граней полок швеллера по ГОСТ 8240-89, рис. 3), отношением двух чисел (например, уклоны 1:20 и 1:4 граней рельса по ГОСТ 8168-75*) или в промилях (например, уклон 5‰ арматуры).

Знак уклона “ “, вершина которого должна быть направлена в сторону уклона, наносят перед размерным числом, располагаемым непосредственно у изображения поверхности уклона, или на полке линии – выноски, как показано на рисунках.

4

Построение уклонов

1. Провести прямую с уклоном i = 1:6 относительно прямой АЕ через точку А, лежащую на прямой АЕ (рис.3).

1

1:6 В

А 1 2 3 4 5 6 С Е

Отложим на прямой АЕ от точки А шесть произвольно выбранных единиц. Через полученную точку В восстановим перпендикуляр к АЕ длиной в одну единицу.

Рис.3

Гипотенуза АС построенного прямоугольного треугольника АВС

является искомой прямой с уклоном 1:6.

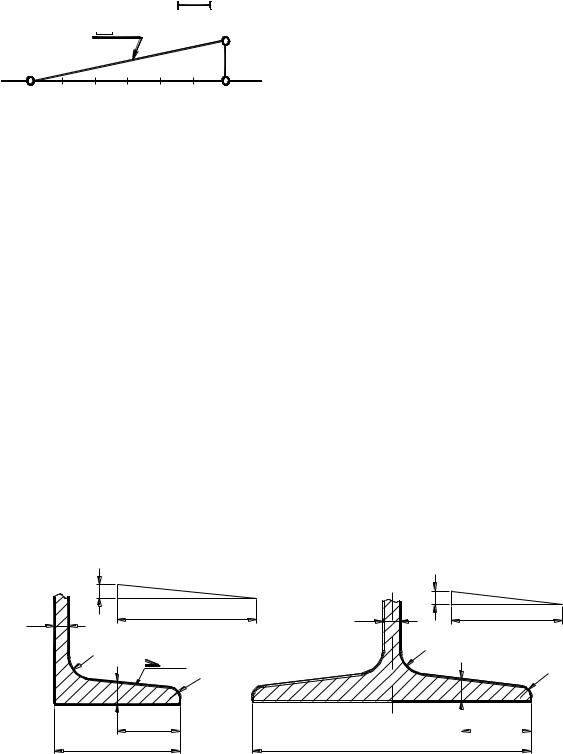
Построение полок швеллера и двутавра

На рис. 4 и 5 показано построение уклона внутренней грани верхней полки швеллера и двутавра. Построен вспомогательный треугольник ВСD с

катетами 10 и 100мм для швеллера и 12 и 100мм для двутавра.

На горизонтальном отрезке «b» отложим отрезок, равный (b-d)/2 – для швеллера и (b-d)/4 – для двутавра. Из полученной точки проведем перпендикуляр длиной t. Отложенные размеры определили положение точки К,

через которую проходит прямая с уклоном 10% для швеллера и 12% — для двутавра. Через точку К провести прямую, параллельную гипотенузе построенного треугольника.

	10
d			100
	R		1:10
			r
		t	(b-d)/2
		b
			Рис.4

	12
d		100
	R
		r

t		(b-d)/4

b

Рис.5

5

КОНУСНОСТЬ

Конусностью называется отношение диаметра окружности основания D

прямого конуса к его высоте h (рис.6).

КDh .

Для усеченного кругового конуса – отношение разности диаметров двух нормальных сечений конуса к расстоянию между ними (рис.7), т.е.

К	D		d	2tg .
		l

K

2

Конусность, как и уклон, может быть выражена отношением целых чисел или в процентах. Перед размерным числом, характеризующим конусность,

наносят знак “ ”, острый угол которого должен быть направлен в сторону вершины конуса.

При одном и том же угле конусность в два раза больше уклона, так как уклон образующей конуса равен отношению радиуса его основания к высоте, а

конусность – отношению диаметра к высоте.

Таким образом, построение конусности i : n относительно данной оси сводится к построению уклонов i : 2n с каждой стороны оси.

6

СОПРЯЖЕНИЯ

Сопряжением называется плавный переход по кривой от одной линии,

прямой или кривой, к другой.

Построение сопряжений основано на свойствах прямых, касательных к окружностям, или на свойствах касающихся между собой окружностей.

Построение касательной к окружности

O

При построении прямой, касательной к

Аокружности в заданной точке С, проводят прямую перпендикулярно к радиусу ОС. При

нахождении центра окружности, касающейся заданной прямой в точке С, проводят через эту точку перпендикуляр к прямой и откладывают на нем величину радиуса заданной окружности (рис.8).

Рис.8

Построение внешней касательной к двум окружностям

Из центра О1 проводят вспомогательную окружность радиусом R3 = R1-R2

и находят точку К. Построение точки К аналогично построению точки С. Точку О1 соединяют с точкой К прямой и проводят параллельную ей прямую из точки О2 до пересечения с окружностью. Точки сопряжения С1 и С2 лежат на пересечении прямых О1К и ранее проведенной линии из центра О2 с

окружностями радиусов R1 и R2 (рис. 9).

С2 В

R2

O2

7

Сопряжение двух дуг окружностей

При внешнем касании двух окружностей расстояние между центрами О1

и О2 равно сумме радиусов R1 и R2. Точка касания С лежит на прямой,

соединяющей центры окружностей (рис.10).

При внутреннем касании окружностей О1О2 = R1 — R2. Точка касания С лежит на продолжении прямой О1О2 (рис.11).

2

R

O1 СO2

С

R1+R2

Рис.10 Рис.11

Сопряжение двух дуг окружностей дугой заданного радиуса

Из центров О1 и О2 описываются дуги вспомогательной окружности радиусом R3 = R + R1 и R4 = R + R2 (при внешнем сопряжении, рис.12)

или R3 = R — R1 и R4 = R — R2 (при внутреннем сопряжении, рис.13). Точка О является центром искомой дуги окружности радиуса R.

Точки сопряжения С1 и С2 будут находиться на линии центров О1О и О2О

(рис.12) или на продолжении линии центров (рис.13).

При нахождении радиуса внешне–внутреннего сопряжения вспомогательные дуги проводятся радиусами R3 = R — R1 из центра О1 и

R4 = R + R2 из центра О2 (рис.14).

Сопряжение окружности с прямой по дуге радиуса R

Из центра О1 проводится дуга радиусом R2 = R1 + R и прямая,

параллельная заданной, на расстоянии R. Пересечение вспомогательной дуги окружности и прямой определит искомый центр О. Точка сопряжения дуг С1

лежит на линии центров О1О, а прямой и дуги сопряжения С – на перпендикуляре, проведенном к заданной прямой из центра О (рис.15).

уклон 1:2 — это… Что такое уклон 1:2?

Уклон — Уклон: Уклон  показатель крутизны склона (а также ската кровли и т. п. в строительстве) Уклон  подземная наклонная горная выработка Уклон реки  отношение падения реки на каком либо участке к длине этого участка Уклон в… …   Википедия

уклон — наклон, склон; отход, курс, настроенность, уклонение, ход, отклонение, линия, установка, крутосклон, характер, откос, направление, косогор, покатость, ориентация, направленность, крен, скос, скат, течение, гласис, устремленность, загиб, выработка …   Словарь синонимов

УКЛОН — в геодезии, показатель крутизны склона; отношение превышения местности к горизонтальному протяжению, на котором оно наблюдается (напр., уклон, равный 0,015, соответствует подъему 15 м на 1000 м расстояния) …   Большой Энциклопедический словарь

уклон — 1. Уклон боковых стенок на поверхности модели, стержневого ящика, стержня или формы (или их частей), который облегчает извлечение деталей из полости формы. 2. Изменение в поперечном сечении, которое встречается при прокатке или холодном… …   Справочник технического переводчика

УКЛОН — УКЛОН, а, муж. 1. То же, что наклон (во 2 знач.). У. столба. Поезд идёт под у. Катиться под у. (также перен.: то же, что катиться по наклонной плоскости). 2. Отклонение от какого н. направления. У. в сторону. 3. перен. Направленность к чему н., к …   Толковый словарь Ожегова

УКЛОН — отношение разности высот двух точек к расстоянию между ними; в жел. дор. практике часть жел. дор. пути, проложенная с наклоном к горизонту …   Технический железнодорожный словарь

УКЛОН — наклонная горная выработка, проходимая с поверхности земли или из подземных выработок. Геологический словарь: в 2 х томах. М.: Недра. Под редакцией К. Н. Паффенгольца и др.. 1978 …   Геологическая энциклопедия

уклон — Угол, образуемый направлением склона с горизонтальной плоскостью в данной точке. Syn.: крутизна склона; угол наклона; крутизна ската …   Словарь по географии

УКЛОН — управление по контролю за легальным оборотом наркотиков Источник: http://www.gzt.ru/topnews/accidents/ generaljskie gallyutsinogeny /131599.html …   Словарь сокращений и аббревиатур

уклон — 2.6. уклон: Измеренный в процентах угол наклона опорной поверхности, образованный поднятой или опущенной одной стороной поверхности и горизонтальной плоскостью таким образом, что линия пересечения опорной поверхности и горизонтальной плоскости… …   Словарь-справочник терминов нормативно-технической документации

уклон —   , а, м. Осуд.   Отклонение, отход от основной линии партии.   == Внутрипартийный уклон. Осуд.   ◘ Мы видим, как победоносно прошла борьба партии со всеми внутрипартийными уклонами (Киров). БАС, т. 16, 459.   == Мелко буржуазный уклон. Осуд. БАС …   Толковый словарь языка Совдепии