Общий случай расчета балки на шарнирных опорах при действии нескольких сосредоточенных нагрузок
Рассмотрим следующий пример: имеется балка перекрытия на двух шарнирных опорах с расчетной длиной l = 230.5 см. На балку опираются 4 лаги, первая на расстоянии l1 = 18 см от шарнирной опоры, расстояние между 1 и 2, между 2 и 3 и между 3 и 4 лагами l2 = l3 = l4 = 60 см, расстояние от 4 лаги до второй шарнирной опоры l5 = 32.5 см.
Как видим, сосредоточенные нагрузки к балке приложены несимметрично, да и значения сосредоточенных нагрузок вряд ли могут быть равными. Как минимум потому, что на лаги передается нагрузка от перекрытия, а значит нагрузка на первую лагу будет меньше, чем на все остальные даже при равномерно распределенной нагрузке на напольное покрытие. А во-вторых, равномерно распределенная нагрузка на напольное покрытие принимается исключительно в целях упрощения расчета, в действительности возле стен обычно стоит всякая разная мебель и потому нагрузка на крайние лаги как правило больше, чем на лаги, расположенные ближе к середине пролета.
Итак у нас есть два варианта проведения расчетов: упрощенный и полный. Сначала рассмотрим
Упрощенный вариант первого этапа расчета балки
Если мы для дальнейшего упрощения расчетов примем значения сосредоточенных нагрузок от лаг равными между собой Q1 = Q2 = Q3 = Q4 = Q = 200 кг, а приложение этих нагрузок будем рассматривать как симметричное, т.е. l1 = l5 = l2/2, то сможем относительно легко перевести эти сосредоточенные нагрузки в эквивалентную равномерно распределенную.
qэкв = γmQ/l = 1·4Q/l = 4·200/230.5 = 3.47 кг/см (305.1.4)
где m — количество сосредоточенных нагрузок, γ = 1 — коэффициент перехода от сосредоточенных нагрузок к эквивалентной равномерно распределенной.
Таким образом максимальный момент составит
M = qэквl2/8 = 3.47·230.52/8 = 23050 кгс·см
и теперь подобрать необходимое сечение будь то деревянной, металлической или железобетонной балки — не проблема (варианты подбора необходимого сечения рассматриваются в соответствующих статьях). Да и определить значения поперечных сил на опорах не сложно. А после того, как будет подобрано необходимое сечение и станут известны его параметры, можно будет проверить допустимость максимального прогиба для такой балки по формуле
Вот в сущности и весь упрощенный расчет, в результате которого мы получили несколько завышенные значения момента. Насколько завышенные, нам поможет узнать
Полный вариант первого этапа расчета балки
1. Определение опорных реакций
Так как первая лага опирается максимально близко к первой шарнирной опоре рассматриваемой балки, то сосредоточенная нагрузка от этой лаги скорее всего будет меньше, чем от остальных лаг. Предположим, что от остальных лаг сосредоточенная нагрузка как и прежде составляет Q2 = Q3 = Q4 = 200 кг, а от первой лаги
Q1 = Q2(l1 + l
Тогда опорные реакции составят
А = (Q1(l — l1) + Q2(l — l1 — l2) + Q3(l4 + l5) + Q4l5)/l = (160(230.5 — 18) + 200((230.5 — 18 — 60) + (60 + 32.5) + 32.5)/230.5 = 388.286 кг
В = (Q1 l1 + Q2( l1 + l2) + Q3(l — l4 — l5) + Q4(l — l5)/l = (160·18 + 200((18 + 60) + (230.5 — 60 — 32.5) + (230.5 — 32.5))/230.5 = 371.713 кг
388.286 + 371.71 = 759.999 ≈ 760 кг = 160 + 3·200
Это значит, что одно из условий равновесия системы выполняется, так как опорные реакции направлены в сторону, противоположную нагрузкам, а значит и сумма всех сил, действующих относительно оси у, будет = 0. Кроме того опорные реакции соответствуют значениям поперечных сил, действующих на опорах балки.
Теперь мы можем продолжать расчет, но сразу отметим, что разница опорных реакций для нашего случая загружения балки не так уж и велика, около
100%(388.286 — 371.713)/371.713 = 4.4%
2. Определение максимального изгибающего момента
Для того, чтобы определить максимальный изгибающий момент при несимметричной нагрузке, мы сначала должны построить эпюру моментов. Впрочем, схема загружения нашей балки не такая уж и сложная и очевидно, что максимальный момент будет в сечении под второй или третьей лагой, поэтому ограничимся тем, что определим значения моментов в сечениях под 2 и 3 сосредоточенной нагрузкой.
М2 = А(l1 + l2) — Q1l2 = 388.286(18 + 60) — 160·60 = 20686.308 кгс·см
М3 = А(l1 + l2 + l3) — Q1(l2 + l3) — Q2l3= 388.286(18 + 60 + 60) — 160(60 + 60) — 200·60 = 22383.468 кгс·см
100%(23050 — 22383.468)/22383.468 = 3%
что можно рассматривать, как дополнительный запас прочности. С учетом того, что при расчетах частно принимаются коэффициенты надежности по нагрузке от 1.1 до 1.4, дополнительный коэффициент 1.03 на мой взгляд не кардинально влияет на расчеты. К тому же доступные сечения деревянного бруса и металлопроката, точнее разница размеров поперечных сечений, иногда требуют принять больший запас по прочности или пересматривать расчетную схему.
Тем не менее продолжим расчет. Для определения максимального прогиба нам сначала нужно определить значение угла поворота поперечного сечения хотя бы на одной из опор, например, на опоре А.
3. Определение угла поворота на опоре А и максимального прогиба поперечного сечения
Так как нагрузки, приложенные к балке, несимметричны и не равны, то максимальный прогиб будет не посредине пролета балки, а в точке, где угол поворота поперечного сечения = 0, где-то между 2 и 3 лагами (на расстоянии х от первой опоры и судя по всему достаточно близко к середине пролета балки). На основании этого мы можем составить следующее уравнение:
θ(х) = — θA + Ax2/2EI — Q1(x — l1)2/2EI — Q2(x — l
В этом уравнении 2 неизвестных: угол поворота на опоре А и собственно расстояние х. Для того, чтобы определить угол поворота на опоре А, необходимо решить дополнительное уравнение, исходя из условия, что прогиб на опорах А и В равен нулю.
fВ = — θAl + Al3/6EI — Q1(l — l1)3/6EI — Q2(l — l1 — l2)3/6EI — Q3(l4 + l5)3/6EI — Q4l53/6EI = 0
После определения этих неизвестных мы, наконец можем определить максимальный прогиб по формуле
f(x) = — θAx + Ax3/6EI — Q1(х — l1)3/6EI — Q2(x — l1 — l2)3/6EI
Лично у меня нет большого желания решать все эти уравнения, тем более, что итоговые результаты будут отличаться от полученных при упрощенном расчете на несколько процентов. А есть ли у вас необходимость в столь точном расчете — решать вам.
Задачи на динамические нагрузки | ПроСопромат.ру
На двутавровой балке установлен электродвигатель весом G=5кН, при работе которого из-за дисбаланса вращающихся частей возникает вертикальная центробежная сила 
Определить наибольшие нормальные напряжения и прогиб.

Решение:
Балка находится под действием двух нагрузок: под действием статической нагрузки – веса двигателя G и под действием динамической (вибрационной) нагрузки F. Поэтому все параметры складываются из статической и динамической составляющих:

Статические составляющие от силы G найдем как обычно при статическом расчете:

Наибольшее статическое напряжение в среднем сечении балки будет:

Для определения статического прогиба среднего сечения выберем вспомогательное состояние и построим эпюру 

Прогиб от статической нагрузки G будет:

Динамические значения параметров от действия вибрационной нагрузки определяются с помощью динамического коэффициента следующим образом:

В формулу динамического коэффициента вибрационной нагрузки входит величина ω – круговая частота собственных (свободных) колебаний, определяемая по формуле:

где: g=9,81м/сек2 –ускорение свободного падения,
Δст – перемещение точки расположения колеблющейся массы (в данном случае двигателя) от собственного веса.

Тогда значение динамического коэффициента вибрационной нагрузки будет:

Здесь круговая частота действия самой вибрационной нагрузки

Далее находим  , для чего к балке прикладывается наибольшая величина вибрационной нагрузки статическим образом:
, для чего к балке прикладывается наибольшая величина вибрационной нагрузки статическим образом:

Прогиб середины пролета в балке на двух опорах можно вычислить и по известной формуле:

Тогда динамические значения искомых параметров будут:

 представляет собой амплитуду колебаний массы (двигателя), то есть наибольшее отклонение от положения статического равновесия. Поэтому наибольшее значение прогиба складывается из статического смещения
представляет собой амплитуду колебаний массы (двигателя), то есть наибольшее отклонение от положения статического равновесия. Поэтому наибольшее значение прогиба складывается из статического смещения  и амплитуды колебаний
и амплитуды колебаний 

Наибольшее нормальное напряжение

Приведение сосредоточенной нагрузки к эквивалентной равномерно распределенной
1 вариант
Расстояние между сосредоточенными нагрузками одинаковое, при этом расстояние от начала пролета до первой сосредоточенной нагрузки равно расстоянию между сосредоточенными нагрузками. В этом случае сосредоточенные нагрузки также попадают на начало и на конец пролета, но при этом вызывают только увеличение опорной реакции, на значение изгибающих моментов и на прогиб крайние сосредоточенные нагрузки никак не влияют, а потому при расчетах несущей способности конструкции не учитываются. Рассмотрим это на примере балок перекрытия опирающихся на перемычку. Кирпичная кладка, которая может быть между перемычкой и балками перекрытия, и создавать при этом равномерно распределенную нагрузку, для простоты восприятия не показана.
Рисунок 1. Приведение сосредоточенных нагрузок к эквивалентной равномерно распределенной нагрузке.
Как видно из рисунка 1, определяющим является изгибающий момент, который используется при расчетах конструкций на прочность. Таким образом, чтобы равномерно распределенная нагрузка создавала такой же изгибающий момент, как и сосредоточенная нагрузка, ее нужно умножить на соответствующий коэффициент перехода (коэффициент эквивалентности). А определяется этот коэффициент из условий равенства моментов. Думаю, рисунок 1 это очень хорошо иллюстрирует. А еще, анализируя полученные зависимости, можно вывести общую формулу для определения коэффициента перехода. Так, если количество приложенных сосредоточенных нагрузок является нечетным, т.е. одна из сосредоточенных нагрузок обязательно попадает на середину пролета, то для определения коэффициента эквивалентности можно использовать формулу:
γ = n/(n — 1) (305.1.1)
где n — количество пролетов между сосредоточенными нагрузками.
При этом эквивалентная равномерно распределенная нагрузка будет равна:
qэкв = γ(n-1)Q/l (305.1.2)
где (n-1) — количество сосредоточенных нагрузок.
Впрочем, иногда удобнее производить расчеты, исходя из количества сосредоточенных нагрузок. Если это количество выразить переменной m, то тогда
γ = (m +1)/m (305.1.3)
где m — количество сосредоточенных нагрузок.
При этом эквивалентная равномерно распределенная нагрузка будет равна:
qэкв = γmQ/l (305.1.4)
Когда количество сосредоточенных нагрузок является четным, т.е. ни одна из сосредоточенных нагрузок не попадает на середину пролета, то значение коэффициента можно принимать, как для следующего нечетного значения количества сосредоточенных нагрузок. В целом при соблюдении указанных условий загружения можно принимать следующие коэффициенты перехода:
γ = 2 — если на рассматриваемую конструкцию, например, балку попадает только одна сосредоточенная нагрузка посредине перемычки.
γ = 1.33 — для балки, на которую действуют 2 или 3 сосредоточенные нагрузки;
γ = 1.2 — для балки, на которую действуют 4 или 5 сосредоточенных нагрузок;
γ = 1.142 — для балки, на которую действуют 6 или 7 сосредоточенных нагрузок;
γ = 1.11 — для балки, на которую действуют 8 или 9 сосредоточенных нагрузок.
2 вариант
Расстояние между сосредоточенными нагрузками одинаковое, при этом расстояние от начала пролета до первой сосредоточенной нагрузки равно половине расстояния между сосредоточенными нагрузками. В этом случае сосредоточенные нагрузки не попадают на начало и на конец пролета.
Рисунок 2. Значения коэффициентов перехода при 2 варианте приложения сосредоточенных нагрузок.
Как видно из рисунка 2, при таком варианте загружения значение коэффициента перехода будет значительно меньше. Так, например, при четном количестве сосредоточенных нагрузок, коэффициент перехода вообще можно принимать равным единице. При нечетном количестве сосредоточенных нагрузок для определения коэффициента эквивалентности можно использовать формулу:
γ = (m +7)/(m +6) (305.2.1)
где m — количество сосредоточенных нагрузок.
При этом эквивалентная равномерно распределенная нагрузка все также будет равна:
qэкв = γmQ/l (305.1.4)
В целом при соблюдении указанных условий загружения можно принимать следующие коэффициенты перехода:
γ = 2 — если на рассматриваемую конструкцию, например, балку попадает только одна сосредоточенная нагрузка посредине перемычки, а попадают ли балки перекрытия на начало или конец пролета или расположены сколь угодно далеко от начала и конца пролета, в данном случае значения не имеет. А значение это имеет при определении сосредоточенной нагрузки.
γ = 1 — если на рассматриваемую конструкцию, действует четное количество нагрузок.
γ = 1.11 — для балки, на которую действуют 3 сосредоточенные нагрузки;
γ = 1.091 — для балки, на которую действуют 5 сосредоточенных нагрузок;
γ = 1.076 — для балки, на которую действуют 7 сосредоточенных нагрузок;
γ = 1.067 — для балки, на которую действуют 9 сосредоточенных нагрузок.
Не смотря на некоторую заковыристость определения, коэффициенты эквивалентности очень просты и удобны. Так как при расчетах очень часто известна распределенная нагрузка, действующая на квадратный или погонный метр, то чтобы не переводить распределенную нагрузку сначала в сосредоточенную, а потом снова в эквивалентную распределенную, достаточно просто умножить значение распределенной нагрузки на соответствующий коэффициент. Например, на перекрытие будет действовать нормативная распределенная нагрузка 400 кг/м2, при этом собственный вес перекрытия составит еще 300 кг/м2. Тогда при длине балок перекрытия 6 м на перемычку могла бы действовать равномерно распределенная нагрузка q = 6(400 + 300)/2 = 2100 кг/м. А дальше, если будет только одна балка перекрытия посредине пролета, то γ = 2, а
qэкв = γq = 2q (305.2.2)
И все.
Если ни одно из двух вышеприведенных условий не соблюдается, то использовать коэффициенты перехода в чистом виде нельзя, нужно добавить еще пару дополнительных коэффициентов, учитывающих расстояние до балок, не попадающих на начало и конец пролета перемычки, а также возможную несимметричность приложения сосредоточенных нагрузок. Вывести такие коэффициенты в принципе можно, однако в любом случае они будут понижающими во всех случаях, если рассматривать 1 вариант загружения и в 50% случаев, если рассматривать 2 вариант загружения, т.е. значения таких коэффициентов будут < 1. А потому для упрощения расчетов, а заодно и для большего запаса по прочности рассчитываемой конструкции вполне хватит коэффициентов, приведенных при первых двух вариантах загружения.
Определение прогиба деревянной балки согласно СП 64.13330.2011
Конечно же, будь моя воля, я бы, перед тем как приводить формулу для определения прогиба изгибаемых элементов с учетом действия поперечных сил, сначала привел бы упрощенную формулу определения прогиба с соответствующим пояснением, что ей можно пользоваться для приблизительного определения прогиба при соотношениях высоты балки к длине h/l < 20.
Тем не менее, к разработке и составлению указанного Свода Правил я никакого отношения не имею, да и вообще до такого уровня просто еще не дорос. А потому считаю, что требования СП следует безусловно выполнять, а как именно это сделать, мы сейчас и узнаем.
Формула для определения прогиба с учетом действия поперечных сил, приведенная в СП, имеет следующий вид:
f = fo[l + c(h/l)2]/k (544.1)
где f0 — значение прогиба, определяемое без учета действия касательных напряжений, т.е. по упрощенной формуле. Формулы для определения прогиба статически определимых балок можно посмотреть здесь. Впрочем для определения прогиба некоторых видов статически неопределимых балок формулы также имеются.
с — коэффициент, учитывающий влияние поперечных сил на прогиб (о том, как определить этот коэффициент, мы поговорим чуть позже).
k — коэффициент, учитывающий возможное изменение высоты сечения по длине балки. При постоянной высоте k = 1.
При этом h — высота поперечного сечения балки, l — длина пролета балки.
Что лично мне не нравится в формуле (544.1)? Только одна маленькая деталь — наличие в квадратных скобках абсолютной величины — длины балки l.
На мой взгляд это делает данную формулу совершенно бессмысленной, так как определяя прогиб f0, измеряемый хоть в метрах хоть в сантиметрах, и умножая его на длину, измеряемую в тех же метрах или сантиметрах, мы получим какую-то абстрактную величину, измеряемую то ли в м2 то ли в см2. Между тем прогиб всегда имеет линейную размерность, т.е. измеряется или в метрах или в сантиметрах.
Полагаю, что это просто опечатка и вместо длины l в формуле должна стоять единица — 1 (действительно 1 и l очень легко спутать). Кроме того, из общих положений теории сопротивления материалов следует, что в общем случае при учете влияния поперечных сил формула для определения прогиба (например, при действии сосредоточенной нагрузки на конце консольной балки) имеет следующий вид:
— fl = Ql3(1 + λ)/3EI (536.13)
где
λ = k(1 + μ)h2/2l2 (536.12)
И тогда коэффициент с это:
с = k(1 + μ)/2 (544.2)
Мне кажется, что это является еще одним подтверждением того, что формула, приведенная в СП, как впрочем и в старом СНиПе, неправильная. А правильный вариант этой формулы должен иметь следующий вид:
f = fo[1 + c(h/l)2]/k (544.1.2)
Тем не менее, как я уже говорил, я не являюсь ни составителем, ни разработчиком указанных нормативных документов, а потому мое мнение — это всего лишь мнение некоего частного лица, учитывать которое не обязательно.
Если у вас получается определить прогиб деревянной балки по приведенной в Своде Правил формуле, то — вперед! Не обращайте на мои сомнения внимания. Ну а для сомневающихся я бы все-таки предложил формулу (544.1.2). Осталось только выяснить, чему же равен коэффициент с.
Древесина не является изотропным материалом. Например значение модуля упругости древесины вдоль и поперек волокон отличается на порядок, чуть ли не на два, и потому для определения значения коэффициента с конечно же следует пользоваться не общими положениями теории сопротивления материалов, а рекомендациями СП.
Так значение коэффициента с следует определять по таблице Е.3 обязательного приложения Е:
Таблица Е.3. Значения коэффициентов k и с для определения прогибов балок с учетом переменности сечений и деформаций сдвига
Тут может возникнуть дополнительный вопрос: а как определить значение коэффициента β, который присутствует чуть ли не во всех формулах данной таблицы?
СП на этот вопрос прямого ответа не дает, однако по контексту таблицы можно догадаться, что
β = h0/h (544.3)
где h — максимальная высота балки (как правило посредине пролета), h0 — высота балки в начале и(или) конце пролета.
Соответственно βh = h0. Так же из приведенной таблицы становится понятным и то, почему при постоянной по всей длине балки высоте сечения, т.е. при β = 1, коэффициент, учитывающий возможное изменение высоты сечения балки, также равен единице — k = 1.
Конечно же в представленной таблице Е.3 представлены далеко не все возможные случаи загружения балок. Как поступать в случаях, когда на балку действуют другие нагрузки, например несимметичные распределенные или сосредоточенные, в СП опять же не объясняется.
Я считаю, что в таких случаях действующие нагрузки следует привести к эквивалентным симметричным равномерно распределенным или сосредоточенным, но это опять же лишь мое личное мнение.
В целом прогиб, определяемый расчетом, должен быть не больше допустимого:
f ≤ fд (544.4)
Значение допустимого прогиба определяется по таблице 19:
Таблица 19
Вот собственно и все, что мне хотелось сказать по поводу определения прогиба согласно требований СП 64.13330.2011 «Деревянные конструкции» (Актуализированная редакция СНиП II-25-80). Конкретные примеры определения прогиба деревянных балок приводятся отдельно.
Консольная балка под действием сосредоточенной нагрузки

Цель: Расчет на изгиб в силовой плоскости под сосредоточенной силой, без учета деформаций поперечного сдвига. Проверяются значения максимальных поперечного перемещения, угла поворота и изгибающего момента.
Файл с исходными данными: 4_1.spr
Формулировка задачи: Консольная балка нагружается на свободном конце сосредоточенной силой Р. Определить максимальные значения поперечного перемещения w, угла поворота θ и изгибающего момента М.
Ссылки: Писаренко Г.С., Яковлев А.П., Матвеев В.В., Справочник по сопротивлению материалов. — Киев: Наук. думка, 1988, стр. 263.
Исходные данные:
| E = 2.0·1011 Па | — модуль упругости, |
| ν = 0.3 | — коэффициент Пуассона, |
| L = 3 м | — длина балки; |
| I = 2.44·10-6 м4 | — момент инерции поперечного сечения; |
| Р = 5 кН | — значение сосредоточенной силы. |
Конечноэлементная модель: Расчетная схема – система общего вида, 10 стержневых элементов типа 5, 11 узлов.
Результаты решения в SCAD:

Эпюра изгибающего момента М (кН·м)
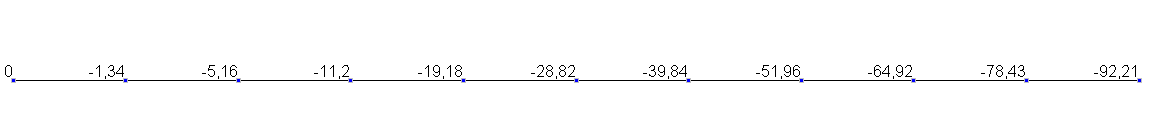
Значения поперечных перемещений w(мм)

Значения углов поворота θ (рад)
Сравнение решений:
Параметр | Теория | SCAD | Отклонения, % |
|---|---|---|---|
Поперечное перемещение w, мм | -92.21 | -92.21 | 0.00 |
Угол поворота θ, рад | 0.04611 | 0.04611 | 0.00 |
Изгибающий момент М, кН·м | -15.0 | -15.0 | 0.00 |
Замечания: При аналитическом решении максимальные значения поперечного перемещения w, угла поворота θ и изгибающего момента М определяются по следующим формулам:
\[ w=-\frac{P\cdot L^{3}}{3\cdot E\cdot I}; \quad \theta =\frac{P\cdot L^{2}}{2\cdot E\cdot I}; \quad M=-P\cdot L. \]
