Длина знак: Длина волны — Википедия – Единицы измерения расстояния — Википедия

Длина волны — Википедия

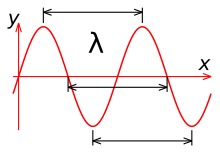График волны функции (например, физической величины) y, распространяющейся вдоль оси Оx, построенный в фиксированный момент времени (t = const). Длина волны λ может быть измерена как расстояние между парой соседних максимумов y (x) либо минимумов, либо как удвоенное расстояние между соседними точками, в которых y = 0

Длина́ волны́ — расстояние между двумя ближайшими друг к другу точками в пространстве, в которых колебания происходят в одинаковой фазе^[1][2].

Длина́ волны́ (в линии передачи) — расстояние в линии передачи, на котором фаза электромагнитной волны вдоль направления распространения меняется на 2π^[3].

Длину волны можно также определить:

• как расстояние, измеренное в направлении распространения волны, между двумя точками в пространстве, в которых фаза колебательного процесса отличается на 2π{\displaystyle 2\pi };
• как путь, который проходит фронт волны за интервал времени, равный периоду колебательного процесса;
• как пространственный период волнового процесса.

Представим себе волны, возникающие в воде от равномерно колеблющегося поплавка, и мысленно остановим время. Тогда длина волны — это расстояние между двумя соседними гребнями волны, измеренное в радиальном направлении. Длина волны — одна из основных характеристик волны наряду с частотой, амплитудой, начальной фазой, направлением распространения и поляризацией. Для обозначения длины волны принято использовать греческую букву λ{\displaystyle \lambda }, размерность длины волны — метр.

Как правило, длина волны используется применительно к гармоническому или квазигармоническому (например, затухающему или узкополосному модулированному) волновому процессу в однородной, квазиоднородной или локально однородной среде. Однако формально длину волны можно определить по аналогии и для волнового процесса с негармонической, но периодической пространственно-временной зависимостью, содержащей в спектре набор гармоник. Тогда длина волны будет совпадать с длиной волны основной (наиболее низкочастотной, фундаментальной) гармоники спектра.

Длина волны — пространственный период волнового процесса[править | править код]

Волна — колебательный процесс, развивающийся (распространяющийся) в пространстве и во времени, в связи с этим изменяющаяся в волновом процессе физическая величина является функцией пространственных координат и времени (то есть особого вида пространственно-временной функцией). Волновой процесс в частности может быть периодическим (например, гармоническим). По аналогии с «временны́м» периодом T{\displaystyle T} [с] (интервалом времени, за который периодический колебательный процесс повторяется) длину волны λ{\displaystyle \lambda } [м] можно рассматривать как

пространственный период волнового процесса. Следует заметить, что «временно́й» круговой частоте ω=2πf=2π/T{\displaystyle \omega =2\pi f=2\pi /T} [радиан/с], показывающей, на сколько радиан изменится фаза колебания за 1 с, соответствует «пространственная круговая частота» k=2π/λ{\displaystyle k=2\pi /\lambda } [радиан/м], называемая волновым числом и показывающая, на сколько радиан отличаются фазы колебательного процесса в двух точках в пространстве, расположенных вдоль направления распространения волны на расстоянии 1 м друг от друга. При этом очевидно, что фазы колебательного процесса в двух таких точках, расположенных друг от друга на расстоянии в λ{\displaystyle \lambda }, отличаются ровно на 2π{\displaystyle 2\pi }.

Получить соотношение, связывающее длину волны с фазовой скоростью v{\displaystyle v} и частотой f{\displaystyle f} можно из определения. Длина волны соответствует пространственному периоду волны, то есть расстоянию, которое точка с постоянной фазой «проходит» за интервал времени, равный периоду T{\displaystyle T} колебаний, поэтому

λ=vT=vf=2πvω.{\displaystyle \lambda =vT={\frac {v}{f}}={\frac {2\pi v}{\omega }}.}

Для электромагнитных волн в вакууме скорость v{\displaystyle v} в этой формуле равна скорости света (299 792 458 м/с), и длина волны λ=299792458 m/sf{\displaystyle \lambda ={\frac {299\,792\,458~{\text{m/s}}}{f}}}. Если значение f{\displaystyle f} подставить в герцах, то λ{\displaystyle \lambda } будет выражена в метрах.

Радиоволны делят на диапазоны по значениям длин волн, например, 10…100 м — декаметровые (короткие) волны, 1…10 м — метровые, 0.1…1,0 м — дециметровые и т. п. Механизмы и условия распространения радиоволн, степень проявления эффекта дифракции, отражающие свойства объектов, предельная дальность радиосвязи и радиолокации сильно зависят от длины волны. Как правило, габаритные размеры антенн сравнимы либо (справедливо всегда для антенн направленного действия) превышают рабочую длину волны радиоэлектронного средства.

В оптически более плотной среде (слой выделен тёмным цветом) длина электромагнитной волны сокращается. Синяя линия — распределение мгновенного (t = const) значения напряжённости поля волны вдоль направления распространения. Изменение амплитуды напряжённости поля, обусловленное отражением от границ раздела и интерференцией падающей и отражённых волн, на рисунке условно не показано.

Длина электромагнитной волны в среде короче, чем в вакууме:

λ=cnν,{\displaystyle \lambda ={\frac {c}{n\nu }},}

где n=εμ>1{\displaystyle n={\sqrt {\varepsilon \mu }}>1} — показатель преломления среды;

ε{\displaystyle \varepsilon } — относительная диэлектрическая проницаемость среды;

μ{\displaystyle \mu } — относительная магнитная проницаемость среды.

Величины n{\displaystyle n}, μ{\displaystyle \mu } и ε{\displaystyle \varepsilon } могут существенно зависеть от частоты ν{\displaystyle \nu } (явление дисперсии). Поскольку для большинства сред в радиочастотном диапазоне μ≈1{\displaystyle \mu \approx 1} (для диэлектриков μ=1{\displaystyle \mu =1}, для ферромагнетиков с ростом частоты μ→1{\displaystyle \mu \rightarrow 1}), то в инженерной практике используют величину 1/ε<1{\displaystyle 1/{\sqrt {\varepsilon }}<1}, которую называют

коэффициентом укорочения. Она равна отношению длины волны в среде к длине волны в вакууме. Например, для полиэтилена (используется в радиочастотном диапазоне как изоляционный материал с малыми потерями) ε{\displaystyle \varepsilon } = 2,56, и коэффициент укорочения 1/ε{\displaystyle 1/{\sqrt {\varepsilon }}} = 1/1,6 = 0,625.

Напротив, длина электромагнитной волны (поперечномагнитной, поперечноэлектрической) в волноводах может быть не только больше, чем в среде с тем же значением ε{\displaystyle \varepsilon }, но и больше, чем вакууме, поскольку фазовая скорость электромагнитной волны в волноводе превышает скорость электромагнитной волны в среде с тем же ε{\displaystyle \varepsilon }.

Волнам де Бройля также соответствует определённая длина волны. Частице с энергией E{\displaystyle E} и импульсом p{\displaystyle p}, соответствуют:

• частота: ν=Eh,{\displaystyle \nu ={\frac {E}{h}},}
• длина волны: λ=hp,{\displaystyle \lambda ={\frac {h}{p}},}

где h{\displaystyle h} — постоянная Планка.

Видеоурок: длина волны

Приближённо, с погрешностью около 0,07 % рассчитать длину радиоволны в свободном пространстве можно так: 300 делим на частоту в мегагерцах, получаем длину волны в метрах. Другой способ — запомнить какую-нибудь удобную пару f{\displaystyle f} ↔ λ{\displaystyle \lambda }, например, частоте 100 МГц соответствует длина волны 3 м; тогда оценив, во сколько раз требуемая частота выше или ниже 100 МГц, можно определить длину волны. Например, 1 МГц ниже 100 МГц в 100 раз, значит 1 МГц ↔ 3 м × 100 = 300 м

Примеры характерных частот и длин волн: частоте 50 Гц (частота тока в электросети) соответствует длина радиоволны 6000 км; частоте 100 МГц (радиовещательный FM-диапазон) — 3 м; 900 (1800) МГц (мобильные телефоны) — 33,3 (16,7) см; 2,4 ГГц (Wi-Fi) — 12,5 см; 10 ГГц (бортовые радиолокационные станции системы управления вооружением современных самолётов-истребителей) — 3 см. Видимый свет представляет собой электромагнитное излучение c длинами волн от 380 до 780 нм

[4].

1. ↑ Колебания и волны // Физика : Учебник для 11 класса общеобразовательных учреждений / Г. Я. Мякишев, Б. Б. Буховцев. — 12-е изд. — М. : Просвещение, 2004. — С. 121. — 336 с. — 50 000 экз. — ISBN 5-09-013165-1.
2. ↑ Определение не вполне корректно, поскольку (1) в одинаковой фазе колебания происходят и на фронте волны, и расстояние между точками на фронте может быть произвольным, в том числе и нулевым; (2) чтобы расстояние между двумя точками равнялось длине волны, колебание должно происходить не в одинаковой фазе, а со сдвигом фаз в 2π{\displaystyle 2\pi }, и расположены точки должны быть вдоль линии распространения
3. ↑ ГОСТ 18238-72. Линии передачи сверхвысоких частот. Термины и определения.
4. ↑ ГОСТ 7601-78. Физическая оптика. Термины, буквенные обозначения и определения основных величин Архивная копия от 23 марта 2013 на Wayback Machine

Единицы измерения расстояния — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 16 апреля 2017; проверки требуют 12 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 16 апреля 2017; проверки требуют 12 правок.

Единицы измерения расстояния[править | править код]

Метрическая система[править | править код]

Единицей измерения расстояния и одной из основных единиц в Международной системе единиц (СИ) является метр. Метр также является единицей измерения расстояния и относится к числу основных единиц в метрических системах МКС, МКСА, МКСК, МКСГ, МСК, МКСЛ, МСС, МКГСС и МТС^[1].

В системе СГС единицей измерения расстояния служит сантиметр.

На практике применяются также кратные и дольные единицы метра, образуемые с помощью стандартных приставок СИ:

Кратные				Дольные
величина	название	обозначение		величина	название	обозначение
101 м	декаметр	дам	dam	10−1 м	дециметр	дм	dm
102 м	гектометр	гм	hm	10−2 м	сантиметр	см	cm
103 м	километр	км	km	10−3 м	миллиметр	мм	mm
106 м	мегаметр	Мм	Mm	10−6 м	микрометр	мкм	µm
109 м	гигаметр	Гм	Gm	10−9 м	нанометр	нм	nm
1012 м	тераметр	Тм	Tm	10−12 м	пикометр	пм	pm
1015 м	петаметр	Пм	Pm	10−15 м	фемтометр	фм	fm
1018 м	эксаметр	Эм	Em	10−18 м	аттометр	ам	am
1021 м	зеттаметр	Зм	Zm	10−21 м	зептометр	зм	zm
1024 м	иоттаметр	Им	Ym	10−24 м	иоктометр	им	ym
применять не рекомендуется      не применяются или редко применяются на практике

Британская/американская система[править | править код]

• Лига (лье) = 4,828032 км
• Миля = 1,609344 км
• Фурлонг = 201,16 м
• Чейн = 20,1168 м
• Род = 5,0292 м
• Ярд = 91,44 см
• Инспекционный фут = 1,000002 фута = 30,48006096 см
• Фут = 30,48 см
• Линк = 20,1168 см
• Хэнд = 10,16 см
• Дюйм = 2,54 см
• Линия большая = 0,254 см
• Линия малая = 0,2116 см
• Мил = 0,0254 мм

Старорусская система[править | править код]

• 1 пядь = 17,78 см
• 2 пяди = 1 стопа (35,56 см)
• 3 пяди = 1 локоть (53,34 см)
• 4 пяди = 1 аршин (71,12 см)
• 5 пядей = 1 шаг (88,9 см)
• 6 пядей = 1 мера или полсаженя (106,68 см)
• 7 пядей = 1 лоб (124,46см) (7 пядей во лбу)
• 8 пядей = 1 столбец (142,24 см)
• 9 пядей = 1 посох (160,02 см)
• 10 пядей = 1 витой посох (177,8 см)
• 12 пядей = 1 сажень (213,36 см) (катет)
• 16 пядей = 1 круг (284,48 см)
• 17 пядей = 1 косая сажень (302,26 см) (гипотенуза)
• ¹/₂ пяди = 1 пясть (8,89 см)
• ¹/₄ пяди = 1 вершок (4,445 см)
• ¹/₁₆ пяди = 1 нокоть (1,11125 см)
• ¹/₂₅₆ пяди (¹/₁₆ ноктя) = 1 линия (0,069453 см)
• ¹/₄₀₉₆ пяди (¹/₁₆ линии) = 1 волос (0,00434 см)
• ¹/₆₅₅₃₆ пяди (¹/₁₆ волоса) = 1 волосок (0,00027 см)
• 1 верста = 6000 пядей (1066,8 метров)
• 1 столбовая верста = 1517,41632 метра
• 1 мерная верста = 1000 саженей (2133,6 метра)
• 1 миля = 7 вёрст (7,4676 км)
• Великая сажень ≈ 244,0 см
• Городовая сажень ≈ 284,8 см
• Греческая сажень ≈ 230,4 см позже приравняли аттический стадий = 6 английских футов 1 дюйм = 185,42 см
• Казённая (мерная, трёхаршинная) сажень. В XVI веке сажень была приравнена к 3 аршинам и стала называться казённой, или трёхаршинной (213,36 см)
• Кладочная сажень ≈ 159,7 см
• Косая сажень — расстояние от пальцев ноги до конца пальцев руки, вытянутой над головой по диагонали ≈ 248 см
• Малая сажень — расстояние от поднятой на уровень плеча руки до пола ≈ 142,4 см
• Маховая сажень — расстояние между вытянутыми пальцами раскинутых (размахнутых) рук. В таких маховых саженях, которые легко отсчитывать, выражена, например, высота колокольни Ивана Великого в Кремле. Эта наиболее древняя мера, начиная с XVI века, перешла в разряд неофициальных, бытовых. = 2,5 аршина = 152—177,8 см
• Морская сажень = 6 английским футам = 182,88 см
• Народная сажень ≈ 176,0 см
• Простая сажень ≈ 150,8 см
• Сажень без чети — наибольшее расстояние между подошвой левой ноги и концом большого пальца поднятой вверх правой руки ≈ 197,2 см
• Трубная сажень — мерили только длину труб на соляных промыслах ≈ 187 см
• Царская сажень ≈ 197,4 см
• Церковная сажень ≈ 186,4 см
• Четырёхаршинная сажень = 4 аршина = 284,48 см

Японская система[править | править код]

• Мо = 0,003030303 см
• Рин = 0,03030303 см
• Бу = 0,3030303 см
• Сун = 3,030303 см
• Сяку = 30,30303 см
• Кэн = 181,8182 см
• Хиро = 181,8182 см
• Дзё = 303,0303 см
• Тё = 10909,09 см
• Ри = 392727.3 см

Древнегреческая система[править | править код]

• Палайста = 7 см
• Плетр = 31 м
• Миля = 1,388 км
• Стадий = 185,136 м
• Плетр = 30,856 м
• Амма = 18,514 м
• Акена (декапод) = 3,086 м
• Оргия (гексапод) = 1,851 м
• Бема (шаг) = 77,14 см
• Пехис (локоть) греческий = 61,712 см
• Пехис (локоть) короткий = 46,284 см
• Пус (фут) = 30,856 см
• Спитам = 23,142 см
• Дихас = 15,428 см
• Палестра (ладонь) = 7,714 см
• Кондиль = 3,857 см
• Дактиль (палец) = 1,928 см
• Стадий олимпийский = 192,27 м
• Стадий аттический = 184,98 м
• Стадий птолемеевский = 185 м

Типографическая система[править | править код]

• твип = 1/20 пункта
• пункт = 0,352777… мм (пункт Adobe) или 0,3759 мм (пункт Дидо) или 0,3515 мм (пункт Хоукса) или 0,375 мм (метрический пункт) или 0,3473 мм (пункт Фурнье)
• цицеро = 12 пунктам (= 4,2333… мм в системе Adobe)
• нонпарель = 5,708 пунктов

Флотская система[править | править код]

Единицы, применяемые в астрономии[править | править код]

Единицы, набранные малым шрифтом, практически не используются или устарели.

Единицы, применяемые в физике[править | править код]

Единицы, применяемые в технике[править | править код]

• юнит = 44,45 мм = 1,75 дюйма;

1. ↑ Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М.: Издательство стандартов, 1990. — С. 77—82. — 240 с. — ISBN 5-7050-0118-5.
2. ↑ Согласно новому определению астрономической единицы, принятому МАС в сентябре 2012 г.
3. ↑ WolframAlpha (неопр.). Архивировано 10 апреля 2013 года.
4. ↑ В скобках указано стандартное отклонение. Таким образом, значение планковской длины можно представить в следующих формах: ℓP{\displaystyle \ell _{P}} ≈ 1,616199(97) · 10⁻³⁵ м =
   = (1,616199 ± 0,000097) · 10⁻³⁵ м =
   = [1,616102 ÷ 1,616296] · 10⁻³⁵ м
5. ↑ NIST, «Planck length» (англ.), NIST’s published CODATA constants
6. ↑ Fundamental Physical Constants — Complete Listing

Длина строки — Википедия

Материал из Википедии — свободной энциклопедии

Примеры различной длины строк. Строка слева (уже) читается быстрее, строка справа (шире) читается медленнее

Длина строки в типографике — ширина блока набранного текста, обычно измеряемая в единицах длины, таких как дюймы или пункты, или в знаках на строку^[en]. Блок текста или абзац имеет максимальную длину строки, вписывающуюся в определённое оформление. Если строки слишком коротки, текст становится слишком разобщённым; если строки слишком длинные, происходит потеря ритма при поиске читателем начала каждой новой строки.

Длина строки определяется типографическими параметрами на основе формальной сетки и макета с несколькими целями: баланс и функциональность для набора и читаемость с учётом эстетических качеств типографики. Типографы подбирают длину строки для удобства чтения или удачного вхождения в набор. Текст может быть выключен по левому краю с рваным правым краем, по правому краю с рваным левым краем или выключен по формату, где все строки будут равной длины. В наборе с рваным правым краем длины строк различаются, чтобы создать рваный правый край строк разной длины. Для выключки по формату и с рваным краем типографы могут настраивать длину строки, чтобы избежать нежелательных дефисов, «коридоров» пробельных символов и оторванных слов или символов на конце строк.

Традиционные исследования длины строки, ограничивавшиеся печатным текстом, сообщали о разных результатах, но обычно для печатного текста принята длина строки от 45 до 75 знаков на строку^[en] (англ. characters per line, cpl), хотя идеальным вариантом является 66 cpl, включая символы и пробелы^[1]. В книжном наборе длина строки обычно равна 30 размерам набора, но считается допустимым набор в пределах 20—40 раз (то есть, 30 × 10-пунктный набор = 300-пунктная строка)^[1]. Ранние исследования считали длину строки в 59—97 мм (около 57 cpl) оптимальной для 10-пунктного набора^[2]. Для печатных работ с несколькими колонками часто лучше 40—50 cpl^[1]. Для текста на английском языке с выключкой по формату минимальное число знаков на строку — 40, длина строки менее 38—40 символов часто приводит к появлению пробелов (или «коридоров») или слишком большого числа переносов слов в блоке текста^[1]. Длинные строки (85—90 cpl) могут быть допустимы для несвязанного текста, например, в библиографиях или сносках, но для непрерывного текста строки в более чем 80 символов могут быть слишком длинными. Короткий текст, например, рваные маргиналии, может быть и длиной в 12—15 знаков на строку^[1]. Исследования показали, что более краткие строки часто предпочитаются длинным, вероятно, потому что участникам более привычен такой формат^[3].

Чтение с экрана создаёт дополнительные проблемы, делая использование традиционных исследований длины текста для электронных форматов проблематичным^[4]. В отличие от печатного текста, дизайн для цифровых носителей должен учитывать такие факторы, как блики, мерцание и прокрутка или перелистывание^[5].

Исследования читаемости цифрового текста показали, что, как и для печатного текста, длина строки может влиять на скорость чтения. Если строки слишком длинные, читателям трудно вернуться к началу следующей строки (саккада), в то время как если они слишком короткие, им требуется больше прокрутки или листания^[6]. Исследователи полагают, что длинные строки лучше подходят для быстрого сканирования, а короткие строки — для точности чтения^[3]. Более длинные строки, в таком случае, лучше подходят для случаев, когда информация будет быстро считываться читателями, а краткие — когда информация предназначена для более тщательного чтения^[3]. Одно из предложений для наилучшего компромисса между скоростью чтения и пониманием — использовать около 55 знаков на строку^[6] В то же время были и исследования, указывавшие, что цифровой текст длиной в 100 знаков может читаться быстрее, чем строки в 25 знаков, сохраняя тот же уровень понимания текста^[4].

Субъективные факторы также играют роль в выборе длины строки для цифрового текста. Одно исследование показало, что число знаков на строку имело незначительное влияние на читаемость, включая факторы скорости и понимания текста, однако при запросе о своих предпочтениях 60 % участников исследования отдали предпочтение самым коротким (35 cpl) или самым длинным (95 cpl) строкам, использованным в исследовании. В то же время 100 % участников выбрали один из этих вариантов как наименее предпочитаемый^[7].

Вторая страница образца шрифта Spartan от American Type Founders^[en] (1953). Измерения алфавита в нижнем регистре для каждого кегля на этой странице показаны в левой колонке

Существует несколько методов расчёта длины строки, соответствующих нужному среднему числу знаков на строку, которое она должна содержать с учётом вышеупомянутых факторов. Большинство методов, если не все из них, используют длину алфавита в нижнем регистре (англ. lowercase alphabet, LCA) в качестве основы для своих расчётов^[8]. Иногда алфавит в нижнем регистре (измерение набора символов гегемонного латинского алфавита от a до z в типографских пунктах) включался в буклеты с образцами шрифтов. Если данные отсутствуют, первым шагом для измерения длины строки во всех этих методах является измерение LCA кеглем шрифта, который будет использоваться в наборе.

1. ↑ ^{1 2 3 4 5} Bringhurst, R. (1992). Horizontal Motion. The Elements of Typographic Style, pp 25-36. Point Roberts, WA: Hartley & Marks.
2. ↑ Tinker, M. A., & Paterson, D. G. (1929). Studies of typographical factors influencing speed of reading. III. Length of line. Journal of Applied Psychology, 13(3), 205—219.
3. ↑ ^{1 2 3} Ling, J., & Van Schaik, P. (2006). The influence of font type and line length on visual search and information retrieval in web pages. International Journal of Human-Computer Studies, 64(5), 395—404.
4. ↑ ^{1 2} Dyson, M. C., & Kipping, G. J. (1998). The Effects of Line Length and Method of Movement on Patterns of Reading from Screen. Visible Language, 32(2), 150—181.
5. ↑ Nanavati, A. A., & Bias, R. G. (2005). Optimal line length in reading — a literature review. Visible Language, 29(2), 121—145.
6. ↑ ^{1 2} Dyson, M. C., & Haselgrove, M. (2001). The influence of reading speed and line length on the effectiveness of reading from screen. International Journal of Human-Computer Studies, 54(4), 585—612.
7. ↑ Shaikh, A. Dawn. The Effects of Line Length on Reading Online News (неопр.) // Usability News. — 2005. — July (т. 7, № 2). Архивировано 19 июня 2015 года.
8. ↑ Robert., Bringhurst. The elements of typographic style (неопр.). — 4th ed. (version 4.0). — Seattle, WA: Hartley & Marks, 2012. — ISBN 9780881792119.

Фут — Википедия

Материал из Википедии — свободной энциклопедии

Длины футов по странам, табл. 1848 г.

Фут (русское обозначение: фут; международное: ft, а также ‘ — штрих; от англ. foot — ступня) — единица измерения длины в английской системе мер. Точное линейное значение различается в разных странах.

В 1958 году на конференции англоговорящих стран страны-участницы унифицировали свои единицы длины и массы. Полученный «международный» фут стал равняться в точности 0,3048 м^[1]. Он чаще всего и подразумевается под «футом» в настоящее время.

Фут является внесистемной единицей и не входит в Международную систему единиц (СИ). В то же время в Российской Федерации фут допускается к применению без ограничения срока наравне с единицами СИ с областью применения «авиационная навигация»^[2].

Фут	Оригинальное наименование	Длина в метрах	Связь с другими единицами
Международный (Великобритания, США)	international foot	0,3048	12 международных дюймов (inches)
Ахенский	Fuß	0,2807
Алстский	Aalsterse voet	0,277
Амстердамский	voet	0,283133	11 дюймов (duimen)
Аргентинский	pie	0,2889
Аугсбургский	Fuß	0,29617
Ашафенбургский	Fuß	0,2905
Баварский	Fuß	0,291859
Баденский	Fuß	0,308
Баденский, метрический	Fuß	0,3
Бельгийский	pied, voet	0,2869
Берлинский	Fuß	0,3097254
Блоисский	Blooise voet	0,301
Богемский	Fuß, stopa	0,296
Болонский	piede	0,380098
Бразильский	pé	0,33
Братиславский		0,316
Бременский	Fuß	0,28935
Британский	foot	0,304799472	12 дюймов (inches)
Брюггский	voet	0,27428
Брюссельский	pied	0,27575
Варшавский или старопольский	stopa staropolska, stopa warszawska	0,2978
Веймарский	Fuß	0,28198
Венгерский	láb	0,316081
Венгерский, королевский	királyi láb	0,3126
Венецианский	piede	0,347735
Венский, австрийский или дунайский	Fuß	0,316081
Веронский	piede	0,342195
Вёрнский	Veurnse voet	0,2728
Вроцлавский	stopa wrocławska	0,288
Вюртембергский	Fuß	0,28649
Гамбургский	Fuß	0,286
Ганноверский	Fuß	0,2921
Гессенский	Fuß	0,25
Греческий-ионический (450 до н. э.)	πούς (род. п. ποδός)	0,308
Дорийский (1200 до.р.х)		0,32686
Дармштадтский	Fuß	0,28814
Датский	Fod	0,3138	12 дюймов (tommer)
Дрезденский	Fuß	0,2831066
Каролингский		0,333
Ипрский	pied	0,2729
Испанский (до 1752)	pie de Ribera, pie de Rey	0,287342	12 дюймов (pulgadas)
Испанский (1752—1765)	pie de Burgos, pie Castellano	0,278635	12 дюймов (pulgadas)
Испанский (после 1765)	pie de Rey	0,32483	12 дюймов (pulgadas)
Итальянский	piede	0,28
Капский	Kaapse voet	0,314858	12 дюймов (duimen)
Квебекский	pied québécois	0,3248406
Кёльнский	Fuß	0,2752112
Киренейский (ионический)		0,3087
Китайский	尺 (chǐ)	0,3181 или 0,358
Китайский, метрический	尺 (chǐ)	0,333333
Краковский	stopa krakowska	0,298
Кортрейкский	Kortrijkse voet	0,2976
Лёвенский	Leuvense voet	0,2855
Лейпцигский	Fuß	0,3826555
Литовский	pėda	0,325
Львовский	Fuß, Stopa galicyjska, stopa lwowska	0,2977
Льежский	pied	0,2918
Майнингский	Fuß	0,30395
Мехеленский	Mechelse voet	0,278
Моравский	stopa	0,2959648
Неапольский	piede	0,264
Нивельский	pied	0,277
Норвежский	fot	0,31375
Нюрнбергский	Fuß	0,30375
Ольденбургский	Fuß	0,29641
Польский	stopa	0,288
Португальский	Fuß	0,3285
Пражский	stopa	0,296416
Прусский	Fuß	0,313853
Пфальцский	Fuß	0,333333
Рейнский	Rheinfuss	0,31387
Римский (новое время)	piede	0,297896
Римский (древний)	pes monetalis (род. п. pedis)	0,2962; 0,296352 или 0,2957
Римский (древний), натуральный	pes naturalis	0,25
Римский (древний), друзский	pes drusianus	0,3327
Роттердамский	voet	0,296
Русский	фут	0,3048	1/7 сажени, 12 дюймов
Саксонский	Fuß	0,28319
силезский	Fuß	0,291002
Схоувский	Schouwse voet	0,311
США, геодезический	survey foot	0,3048006096	12 дюймов (inches)
Техасский	pie	0,2822	1/3 вары (vara)
Тирольский	Fuß	0,3141109
Турнский	pied	0,29777
Финский (равен шведскому)	jalka	0,297
Франкфуртский	Fuß	0,28461
Французский, Парижский	pied	0,3001	12 дюймов (pouces)
Французский, королевский	pied du roi	0,324839385	12 дюймов (pouces)
Хертогенбосский	(‘s Hertogen)bossche voet	0,287
Хильдбургхаузенский	Fuß	0,30385
Шведский	fot	0,296904
Швейцарский	Fuß	0,3
Эноский	pied	0,2934
Японский	尺 (shaku)	0,30303	10 сунов (寸)

Геометрический фут введён в Англии в XVI веке как ширина шестидесяти четырёх ячменных зёрен.

До введения метрической системы фут определялся в Европе чаще как 12 дюймов/пальцев (реже 10 или 16).
Длина ступни как единица измерения использовалась в большинстве древних культур. Первые стандарты таких мер известны в Шумере, где определение дано по ступне статуи правителя Гудеа Лагашского в XXII веке до н. э. Некоторые метрологи считают, что этот фут был заимствован из египетской системы мер и адаптирован греками как поэс (греч. ποῦς, примерно 296—330 мм)^[3], который впоследствии был стандартизован под властью римлян как пес (лат. pes) — 296 мм^[4].

В соответствии с Постановлением Правительства РФ от 31 октября 2009 г. N 879 русским обозначением единицы измерения «фут» является «фут», то есть в данном случае обозначение единицы совпадает с её наименованием^[2]. В то же время на практике часто используется международное обозначение: такой же штрих, как в обозначении угловых минут (‘), ставящийся без пробела за числовым значением, например: 3’ (3 фута).

Метр — Википедия

Метр (русское обозначение: м; международное: m; от др.-греч. μέτρον «мера, измеритель») — единица измерения длины в Международной системе единиц (СИ), одна из семи основных единиц СИ. Также является единицей длины и относится к числу основных единиц в системах МКС, МКСА, МКСК, МКСГ, МСК, МКСЛ, МСС, МКГСС и МТС. Кроме того, во всех упомянутых системах метр — единица коэффициента трения качения, длины волны излучения, длины свободного пробега, оптической длины пути, фокусного расстояния, комптоновской длины волны, длины волны де Бройля и других физических величин, имеющих размерность длины^[1].

Согласно действующему определению, метр есть длина пути, проходимого светом в вакууме за интервал времени 1/299 792 458 секунды^[2][3].

Современное определение метра в терминах времени и скорости света было принято XVII Генеральной конференцией по мерам и весам (ГКМВ) в 1983 году^[2][3].

Метр — длина пути, проходимого светом в вакууме за интервал времени 1/299 792 458 секунды.

Из этого определения следует, что в СИ скорость света в вакууме принята равной в точности 299 792 458 м/с. Таким образом, определение метра, как и два столетия назад, вновь привязано к секунде, но на этот раз с помощью универсальной мировой константы.

Изменения определений основных единиц СИ 2018—2019 годов не затронуло метр с содержательной точки зрения, однако из стилистических соображений было принято формально новое определение, полностью эквивалентное предыдущему^[4]:

Метр, обозначение м, является единицей длины в СИ; его величина устанавливается фиксацией численного значения скорости света в вакууме c{\displaystyle c} равным в точности 299 792 458, когда она выражена единицей СИ м·с⁻¹, где секунда определена через частоту перехода в цезии ΔνCs{\displaystyle \Delta \nu _{\text{Cs}}}.

В соответствии с полным официальным описанием СИ, содержащемся в действующей редакции Брошюры СИ (фр. Brochure SI, англ. The SI Brochure), опубликованной Международным бюро мер и весов (МБМВ), десятичные кратные и дольные единицы метра образуются с помощью стандартных приставок СИ^[5]. «Положение о единицах величин, допускаемых к применению в Российской Федерации», принятое Правительством Российской Федерации, предусматривает использование в РФ тех же приставок^[6].

Кратные				Дольные
величина	название	обозначение		величина	название	обозначение
101 м	декаметр	дам	dam	10−1 м	дециметр	дм	dm
102 м	гектометр	гм	hm	10−2 м	сантиметр	см	cm
103 м	километр	км	km	10−3 м	миллиметр	мм	mm
106 м	мегаметр	Мм	Mm	10−6 м	микрометр	мкм	µm
109 м	гигаметр	Гм	Gm	10−9 м	нанометр	нм	nm
1012 м	тераметр	Тм	Tm	10−12 м	пикометр	пм	pm
1015 м	петаметр	Пм	Pm	10−15 м	фемтометр	фм	fm
1018 м	эксаметр	Эм	Em	10−18 м	аттометр	ам	am
1021 м	зеттаметр	Зм	Zm	10−21 м	зептометр	зм	zm
1024 м	иоттаметр	Им	Ym	10−24 м	иоктометр	им	ym
применять не рекомендуется      не применяются или редко применяются на практике

Соотношение с другими единицами длины[править | править код]

Метрическая единица, выраженная через единицу, не входящую в СИ					Единица, не входящая в СИ, выраженная через метрическую единицу
1 метр	≈	39,37	дюйма		1 дюйм	≡	0,0254	метра
1 сантиметр	≈	0,3937	дюйма		1 дюйм	≡	2,54	сантиметра
1 миллиметр	≈	0,03937	дюйма		1 дюйм	≡	25,4	миллиметра
1 метр	≡	1⋅1010	ангстрем		1 ангстрем	≡	1⋅10−10	метра
1 нанометр	≡	10	ангстрем		1 ангстрем	≡	100	пикометров

Один из публичных эталонов метра, установленных на улицах Парижа в 1795—1796 гг.

В Европе со времён распада империи Карла Великого не существовало общих стандартных мер длины: они могли быть стандартизированы в пределах одной юрисдикции (которая зачастую имела размеры одного торгового городка), но единых мер не было, и каждый регион мог иметь свои собственные. Причиной этого служило в какой-то мере то, что меры длины использовались в налогообложении (налог, например, мог измеряться в определённой длине полотна), а поскольку каждый местный правитель вводил свои налоги, то для соответствующей местности законами устанавливались свои единицы измерений^[8].

С развитием науки в XVII веке стали раздаваться призывы к введению «универсальной меры» (universal measure, как назвал её английский философ и лингвист Джон Уилкинс в своём эссе 1668 года^[9]) или «католического метра» (metro cattolico) итальянского учёного и изобретателя Тито Ливио Бураттини из его работы Misura Universale 1675 года^{[Комм. 1][10]}), меры, которая бы основывалась на каком-либо естественном явлении, а не на постановлении властьдержащей персоны, и которая была бы десятичной, что заменило бы множество разнообразных систем счисления, например, распространённую двенадцатеричную, одновременно существовавших в то время.

Метр — длина маятника[править | править код]

Идея Уилкинса заключалась в том, чтобы выбрать для единицы длины длину маятника с полупериодом колебаний равным 1 с. Подобные маятники были незадолго до этого продемонстрированы Христианом Гюйгенсом, и их длина была весьма близка к длине современного метра (так же, как к единицам длины, использовавшимся в те времена, например, ярду). Однако, вскоре было обнаружено, что длина, измеренная таким способом, различается в зависимости от места измерений. Французский астроном Жан Рише во время экспедиции в Южную Америку (1671—1673) обнаружил увеличение периода колебаний секундного маятника по сравнению с тем, который наблюдался в Париже. Выверенный в Париже маятник в процессе наблюдений им был сокращён на 1,25 французской линии (~ 2,81 мм), дабы избежать отставания во времени на 2 минуты в день. Это было первое прямое доказательство уменьшения силы тяжести по мере приближения к экватору, и это дало разницу в 0,3 % длины между Кайенной (во французской Гвиане) и Парижем^[11].

Вплоть до французской революции 1789 года в вопросе установления «универсальной меры» не было никакого прогресса. Франция была озабочена вопросом распространения единиц измерений длины, необходимость реформы в этой области поддерживали самые различные политические силы. Талейран возродил идею о секундном маятнике и предложил её Учредительному собранию в 1790 году, с тем уточнением, что эталон длины будет измерен на широте 45° N (примерно между Бордо и Греноблем). Таким образом, метр получал следующее определение: метр — это длина маятника с полупериодом колебаний на широте 45°, равным 1 с (в единицах СИ эта длина равна g/π² · (1 с)² ≈ 0,994 м).

Первоначально за основу было принято это определение (8 мая 1790, Французское Национальное собрание). Но несмотря на поддержку собрания, а также поддержку Великобритании и новообразованных Соединённых Штатов, предложение Талейрана так и не было осуществлено^{[12][Комм. 2]}.

Метр — часть Парижского меридиана[править | править код]

Крепость Монжуик — южный конец дуги меридиана

Вопрос реформы единиц измерения был отдан на рассмотрение Французской академии наук, которая создала специальную комиссию, возглавляемую инженером и математиком Жаном-Шарлем де Борда. Борда был ярым приверженцем перехода на десятичную систему исчисления: он усовершенствовал лимб повторительного теодолита, который позволял намного улучшить точность измерения углов на местности, и настаивал, чтобы инструмент калибровался в градах (¹⁄₁₀₀ четверти круга), а не в градусах, чтобы град делился на 100 минут, а минута — на 100 секунд^[13]. Для Борда метод секундного маятника был неудовлетворительным решением, поскольку он основывался на существовавшей в то время секунде — недесятичной единице, которая не подходила для предлагавшейся к внедрению системы десятичного времени — системе, когда в одних сутках 10 часов, в часе 100 минут, а в минуте 100 секунд.

Вместо метода секундного маятника комиссия — среди членов которой были Жозеф Луи Лагранж, Пьер-Симон Лаплас, Гаспар Монж и Кондорсе — решила, что новая единица измерения должна быть равна одной десятимиллионной расстояния от Северного полюса до экватора (четверть земной окружности), измеренного вдоль меридиана, проходящего через Париж^[12]. Помимо той выгоды, что это решение давало лёгкий доступ для французских геодезистов, существовало такое важное достоинство, что часть расстояния от Дюнкерка до Барселоны (около 1000 км, то есть одна десятая от общего расстояния) могла быть проложена от начальных и конечных точек, расположенных на уровне моря, а как раз эта часть находилась в середине четверти окружности, где влияние формы Земли, которая не является правильным шаром, а сплюснута, было бы наибольшим^[12].

30 марта 1791 предложение определить метр через длину меридиана было принято следующим: одна сорокамиллионная часть Парижского меридиана (то есть одна десятимиллионная часть расстояния от северного полюса до экватора по поверхности земного эллипсоида на долготе Парижа). Интересно, что в современных единицах это 11,00000000005{\displaystyle {\frac {1}{1{,}000\,000\,000\,05}}} метра. Идея привязать единицу измерения длины к меридиану Земли была не нова: аналогичным образом ранее были определены морская миля и лье.

Вновь определённая единица получила наименование «метр подлинный и окончательный» (фр. metre vrai et définitif)^[1].

7 апреля 1795 Национальный Конвент принял закон о введении метрической системы во Франции и поручил комиссарам, в число которых входили Ш. О. Кулон, Ж. Л. Лагранж, П.-С. Лаплас и другие учёные, выполнить работы по экспериментальному определению единиц длины и массы. В 1792—1797 годах по решению революционного Конвента французские учёные Деламбр (1749—1822) и Мешен (1744—1804) за 6 лет измерили дугу парижского меридиана длиной в 9°40′ от Дюнкерка до Барселоны, проложив цепь из 115 треугольников через всю Францию и часть Испании. Впоследствии, однако, выяснилось, что из-за неправильного учёта полюсного сжатия Земли эталон оказался короче на 0,2 мм; таким образом, длина меридиана лишь приблизительно равна 40 000 км.

Первый прототип эталона метра был изготовлен из латуни в 1795 году.

Следует отметить, что единица массы (килограмм, определение которого было основано на массе 1 дм³ воды), тоже была привязана к определению метра.

В 1799 году был изготовлен из платины эталон метра, длина которого соответствовала одной сорокамиллионной части Парижского меридиана^[14].

Во время правления Наполеона метрическая система распространилась по многим странам Европы. Выгода от её применения была столь очевидна, что и после отстранения Наполеона от власти принятие метрических единиц продолжалось^[15]:

• 1816 — Бельгия и Голландия;
• 1832 — Португалия;
• 1849 — Испания и Греция;
• 1870 — Германия;
• 1873 — Австрия;
• 1875 — Швейцария.

К концу XIX века из крупных стран только в Великобритании (и её колониях), США, России, Китае и Османской империи остались традиционные меры длины.

На метре как единице длины и килограмме как единице массы была основана метрическая система, которая была введена «Метрической конвенцией», принятой на Международной дипломатической конференции 17 государств (Россия, Франция, Великобритания, США, Германия, Италия и др.) 20 мая 1875 года^[16].

В 1889 году был изготовлен более точный международный эталон метра. Этот эталон изготовлен из сплава 90 % платины и 10 % иридия^[17] и имеет поперечное сечение в виде буквы «X». Его копии были переданы на хранение в страны, в которых метр был признан в качестве стандартной единицы длины.

Дальнейшее развитие[править | править код]

В 1960 было решено отказаться от использования изготовленного людьми предмета в качестве эталона метра, и с этого времени по 1983 год метр определялся как число 1 650 763,73, умноженное на длину волны оранжевой линии (6 056 Å) спектра, излучаемого изотопом криптона ⁸⁶Kr в вакууме. После принятия нового определения платино-иридиевый прототип метра продолжают хранить в Международном бюро мер и весов в тех условиях, что были определены в 1889 году. Однако теперь его статус стал иным: длина прототипа перестала считаться в точности равной 1 м и её фактическое значение должно определяться экспериментально. По своему первоначальному назначению прототип больше не используется.

К середине 1970-х годов был достигнут значительный прогресс в определении скорости света. Достаточно сказать, что если в 1926 году погрешность наиболее точных на то время измерений, выполненных А. Майкельсоном, составляла 4000 м/с^[18], то в 1972 году сообщалось о снижении погрешности вплоть до 1,1 м/с^[19]. После многократной проверки полученного результата в различных лабораториях XV Генеральная конференция по мерам и весам в 1975 году рекомендовала использовать в качестве значения скорости света в вакууме величину, равную 299 792 458 м/с с относительной погрешностью 4·10⁻⁹, что соответствует абсолютной погрешности 1,2 м/с^[20]. Впоследствии в 1983 году именно это значение XVII Генеральная конференция по мерам и весам положила в основу нового определения метра^[2].

Определения метра с 1795 года^[21]

Основа	Дата	Абсолютная погрешность	Относительная погрешность
1⁄10 000 000 часть четверти Парижского меридиана, определённая по результатам измерений, проведённых Деламбром и Мешеном	1795	0,5—0,1 мм	10−4
Первый эталон Metre des Archives из платины	1799	0,05—0,01 мм	10−5
Платино-иридиевый профиль при температуре таяния льда (1-я ГКМВ)	1889	0,2—0,1 мкм	10−7
Платино-иридиевый профиль при температуре таяния льда и атмосферном давлении, поддерживаемый двумя роликами (VII ГКМВ)	1927	неизв.	неизв.
1 650 763,73 длины волны оранжевой линии (6056 Å) спектра, излучаемого изотопом криптона 86Kr в вакууме (XI ГКМВ)	1960	4 нм	4·10−9[2]
Длина пути, проходимого светом в вакууме за (1/299 792 458) секунды (XVII ГКМВ)	1983	0,1 нм	10−10

Погонный метр — единица измерения количества длинномерных объектов (так называемых погонажных изделий, материалов и т. п.), соответствующая куску или участку длиной 1 метр. Погонный метр ничем не отличается от обычного метра, это единица, которой измеряют длину материала независимо от ширины. Погонным метром могут, например, измерять кабельные каналы, доски, листы металла, трубы, плинтусы, оконные уплотнители, ткани. Хотя для тканей правильнее было бы измерять их площадь, но если ширина ткани подразумевается известной и постоянной — используется понятие «погонный метр» (как правило, ширина ткани составляет 1,4 м, и, таким образом, погонный метр ткани является куском 1,0×1,4 м). Говоря строго, в быту чаще используется понятие именно погонного метра, информация о ширине или высоте предметов подразумевается известной или не важной. Наименование погонного метра выделяется в специальной литературе либо для создания различной экспрессивной окраски речи.

Метрологическая литература не рекомендует использовать термин «погонный метр». Общее правило заключается в том, что в случае необходимости поясняющие слова должны входить в наименование физической величины, а не в наименование единицы измерения. Поэтому, например, следует писать «погонная длина равна 10 м», а не «длина равна 10 пог. м»^[22].

Комментарии

1. ↑ metro cattolico (lit. «catholic [в значении „универсальная“] мера»), заимствовано из греческого μέτρον καθολικόν (métron katholikón)
2. ↑ Идея секундного маятника для назначения стандартной длины тем не менее окончательно не умерла, и такой стандарт был использован для определения длины ярда в Великобритании в период 1843—1878 годов.

Источники

1. ↑ ^{1 2} Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М.: Издательство стандартов, 1990. — С. 77—82. — 240 с. — ISBN 5-7050-0118-5.
2. ↑ ^{1 2 3 4} Определение метра (англ.) Резолюция 1 XVII Генеральной конференции по мерам и весам (1983)
3. ↑ ^{1 2} Положение о единицах величин, допускаемых к применению в Российской Федерации. Основные единицы Международной системы единиц (СИ) (неопр.) (недоступная ссылка). Федеральный информационный фонд по обеспечению единства измерений. Росстандарт. Дата обращения 28 февраля 2018. Архивировано 18 сентября 2017 года.
4. ↑ SI base units (неопр.) (недоступная ссылка). BIPM. Дата обращения 22 июня 2019. Архивировано 23 декабря 2018 года.
5. ↑ SI brochure Официальное описание СИ на сайте Международного бюро мер и весов
6. ↑ Положение о единицах величин, допускаемых к применению в Российской Федерации. Десятичные множители, приставки и обозначения приставок… (неопр.) (недоступная ссылка). Федеральный информационный фонд по обеспечению единства измерений. Росстандарт. Дата обращения 28 февраля 2018. Архивировано 18 сентября 2017 года.
7. ↑ Окунь Л. Б. Слабое взаимодействие // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1994. — Т. 4: Пойнтинга — Робертсона — Стримеры. — С. 552—556. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
8. ↑ Nelson, Robert A. (1981), «Foundations of the international system of units (SI)», Phys. Teacher: 596–613, <http://plato.if.usp.br/1-2009/fmt0159n/PDFFiles/ThePhysTeacher_FoundationsOfTheSI.pdf>  Архивная копия от 6 июля 2011 на Wayback Machine.
9. ↑ Wilkins, John (1668), An Essay Towards a Real Character, And a Philosophical Language, London: Gillibrand, <http://www.metricationmatters.com/docs/WilkinsTranslationLong.pdf> .
10. ↑ Misura Universale, 1675 .
11. ↑ Poynting, John Henry & Thompson, Joseph John (1907), A Textbook of Physics: Properties of Matter (4th ed.), London: Charles Griffin, с. 20, <https://books.google.com/books?id=TL4KAAAAIAAJ&pg=PA20> .
12. ↑ ^{1 2 3} Grand dictionnaire universel du XIXe siècle, Paris: Pierre Larousse, 1866—1877, p. 163—164.
13. ↑ Jean Charles de Borda, MacTutor, <http://www-history.mcs.st-andrews.ac.uk/Biographies/Borda.html>. Проверено 13 августа 2010. .
14. ↑ Brief history of the SI (англ.). International Bureau of Weights and Measures. Дата обращения 12 июля 2010. Архивировано 21 августа 2011 года.
15. ↑ Гевара И., Карлес П. Измерение мира. Календари, меры длины и математика.. — М.: Де Агостини, 2014. — С. 125—126. — 160 с. — (Мир математики: в 45 томах, том 38). — ISBN 978-5-9774-0733-5.
16. ↑ Метрическая система мер (неопр.) (недоступная ссылка). История измерений. Дата обращения 12 июля 2010. Архивировано 27 октября 2011 года.
17. ↑ ПЛАТИНА — статья из энциклопедии «Кругосвет»
18. ↑ Ландсберг Г. С. Оптика. — М.: Физматлит, 2003. — С. 387. — ISBN 5-9221-0314-8.
19. ↑ Evenson K. M., Wells J. S., Petersen F. R., Danielson B. L., Day G. W. Speed of Light from Direct Frequency and Wavelength Measurements of the Methane-Stabilized Laser (англ.) // Phys. Rev. Lett.. — 1972. — Vol. 29, no. 19. — P. 1346—1349. — DOI:10.1103/PhysRevLett.29.1346.
20. ↑ Рекомендованное значение скорости света (англ.) Резолюция 2 XV Генеральной конференции по мерам и весам (1975)
21. ↑ Encydopaedia of scientific units, weights, and measures: their SI equivalences and origins. — Springer, 2004. — P. 5. — ISBN 1-85233-682-X.
22. ↑ Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М.: Издательство стандартов, 1990. — С. 78. — 240 с. — ISBN 5-7050-0118-5.

• Cardarelli, Francois (2003). Encydopaedia of scientific units, weights, and measures: their SI equivalences and origins, Springer-Verlag London Limited, ISBN 1-85233-682-X, page 5, table 2.1, data from Giacomo, P., Du platine a la lumiere, Bull. Bur. Nat. Metrologie, 102 (1995) 5-14.
• Humerfelt, Sigurd. (26 October 2010).
• Layer, H.P. (2008). Length—Evolution from Measurement Standard to a Fundamental Constant. Gaithersburg, MD: National Institute of Standards and Technology. Retrieved 18 August 2008.
• Mohr, P., Taylor, B.N., and David B. Newell, D. (13 November 2012). CODATA Recommended Values of the Fundamental Physical Constants: 2010. Gaithersburg, MD: National Institute of Standards and Technology.
• National Institute of Standards and Technology. (December 2003). The NIST Reference on Constants, Units, and Uncertainty: International System of Units (SI) (web site):
• National Institute of Standards and Technology. (27 June 2011). NIST-F1 Cesium Fountain Atomic Clock. Author.
• National Physical Laboratory. (25 March 2010). Iodine-Stabilised Lasers. Author.
• Naughtin, Pat. (2008). Spelling metre or meter. Author.
• Taylor, B.N. and Thompson, A. (Eds.). (2008a). The International System of Units (SI). United States version of the English text of the eighth edition (2006) of the International Bureau of Weights and Measures publication Le Système International d’ Unités (SI) (Special Publication 330). Gaithersburg, MD: National Institute of Standards and Technology. Retrieved 18 August 2008.
• Taylor, B.N. and Thompson, A. (2008b). Guide for the Use of the International System of Units (Special Publication 811). Gaithersburg, MD: National Institute of Standards and Technology. Retrieved 23 August 2008.
• Tibo Qorl. (2005) The History of the Meter (Translated by Sibille Rouzaud). Retrieved 18 August 2008.
• Zagar, B.G. (1999). Laser interferometer displacement sensors in J.G. Webster (ed.). The Measurement, Instrumentation, and Sensors Handbook. CRC Press. isbn=0-8493-8347-1.
• Белобров В.А. (2019). История метра (короткая версия), История метра (полная версия)

длина знака — это… Что такое длина знака?

Длина дуги — Дифференциальная геометрия кривых раздел дифференциальной геометрии, который занимается исследованием гладких пространственных и плоских кривых в евклидовом пространстве аналитическими методами. Содержание 1 Способы задания кривой 1.1 Плоские… …   Википедия

Длина дуги кривой — Дифференциальная геометрия кривых раздел дифференциальной геометрии, который занимается исследованием гладких пространственных и плоских кривых в евклидовом пространстве аналитическими методами. Содержание 1 Способы задания кривой 1.1 Плоские… …   Википедия

Дебаевская длина — (дебаевский радиус) расстояние, на которое распространяется действие электрического поля отдельного заряда в нейтральной среде, состоящей из положительно и отрицательно заряженных частиц (плазма, электролиты). Вне сферы радиуса дебаевской длины… …   Википедия

Герой Монгольской Народной Республики — Герой Монгольской Народной Республики …   Википедия

Знак «Командир подводной лодки» — учреждён приказом НК ВМФ СССР № 170 от 12 июня 1942 г.Знак представляет изображение подводной лодки типа «Щ», в центре которой помещена красная звезда с золотым серпом и молотом посредине. Длина знака 70 мм, наибольшая высота 17 мм.… …   Википедия

Знак «Командир подводной лодки» — В этой статье не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. Вы можете …   Википедия

Знак «Командир подводной лодки» — Знак «Командир подводной лодки» учреждён приказом НК ВМФ СССР № 170 от 12 июня 1942 г. Знак представляет изображение подводной лодки типа «Щ», в центре которой помещена красная звезда с золотым серпом и молотом посредине. Длина знака 70 мм,… …   Википедия

ГКИНП 02-121-79: Руководство по дешифрированию аэроснимков при топографической съемке и обновлении планов масштабов 1:2000 и 1:5000 — Терминология ГКИНП 02 121 79: Руководство по дешифрированию аэроснимков при топографической съемке и обновлении планов масштабов 1:2000 и 1:5000: 7.8.43. «Кусты» свай в воде остатки свайных мостов, некоторых плотин и других сооружений на реках с… …   Словарь-справочник терминов нормативно-технической документации

определение — 2.7 определение: Процесс выполнения серии операций, регламентированных в документе на метод испытаний, в результате выполнения которых получают единичное значение. Источник …   Словарь-справочник терминов нормативно-технической документации

ГОСТ Р ИСО/МЭК 2382-23-2004: Информационная технология. Словарь. Часть 23. Обработка текста — Терминология ГОСТ Р ИСО/МЭК 2382 23 2004: Информационная технология. Словарь. Часть 23. Обработка текста оригинал документа: 23.06.22 автоматическая нумерация параграфов [automatic paragraph numbering]: Возможность текстового процессора… …   Словарь-справочник терминов нормативно-технической документации

Знак ранения — (Знак числа ранений)[1]  отличительный наградной знак (нагрудный знак и не только) военнослужащих ВС России (Русской Армии и Флота, Вооружённых Сил СССР (ВС СССР)), получивших ранения на фронтах Великой войны, Великой Отечественной войны и… …   Википедия

Список физических величин — Википедия

Производные величины	Символ	Описание	Единица СИ	Примечания
Площадь	S	Размер пространства ограниченного замкнутой линией и опирающейся на эту линию поверхностью	м2
Объём	V	Размер пространства заключённого в трёхмерном объекте	м3	экстенсивная величина
Скорость	v	Изменение положения тела в единицу времени	м/с	вектор
Ускорение	a	Изменение скорости в единицу времени	м/с²	вектор
Импульс	p	Количество движения тела	кг·м/с	экстенсивная, сохраняющаяся величина
Сила	F	Мера взаимодействия материи	кг·м/с2 (ньютон, Н)	вектор
Механическая работа	A	Скалярное произведение силы и перемещения.	кг·м2/с2 (джоуль, Дж)	скаляр
Энергия	E	Способность тела или системы совершать работу.	кг·м2/с2 (джоуль, Дж)	экстенсивная, сохраняющаяся величина, скаляр
Мощность	P	Быстрота совершения работы.	кг·м2/с3 (ватт, Вт)
Давление	p	Сила, действующая на единицу площади поверхности перпендикулярно этой поверхности	кг/(м·с2) (паскаль, Па)	интенсивная величина
Плотность	ρ	Масса на единицу объёма.	кг/м3	интенсивная величина
Поверхностная плотность	ρA	Масса на единицу площади.	кг/м2
Линейная плотность	ρl	Масса на единицу длины.	кг/м
Количество теплоты	Q	Энергия, передаваемая от одного тела к другому немеханическим путём	кг·м2/с2 (джоуль, Дж)	скаляр
Электрический заряд	q	Способность тел быть источником электромагнитного поля и принимать участие в электромагнитном взаимодействии	А·с (кулон, Кл)	экстенсивная, сохраняющаяся величина
Напряжение	U	Изменение потенциальной энергии, приходящееся на единицу заряда.	м2·кг/(с3·А) (вольт, В)	скаляр
Электрическое сопротивление	R	Сопротивление объекта прохождению электрического тока	м2·кг/(с3·А2) (ом, Ом)	скаляр
Магнитный поток	Φ	Величина, учитывающая интенсивность магнитного поля и занимаемую им область.	кг·м2/(с2·А) (вебер, Вб)
Частота	ν	Число повторений события за единицу времени.	с−1 (герц, Гц)
Угол	α	Величина изменения направления.	радиан (рад)
Угловая скорость	ω	Скорость изменения угла.	с−1 (радиан в секунду)
Угловое ускорение	ε	Изменение угловой скорости в единицу времени	с−2 (радиан на секунду в квадрате)
Момент инерции	I	Мера инертности объекта при вращении.	кг·м2	тензорная величина
Момент импульса	L	Мера вращения объекта.	кг·м2/c	сохраняющаяся величина
Момент силы	M	Произведение силы на длину перпендикуляра, опущенного из точки на линию действия силы.	кг·м2/с2	вектор
Телесный угол	Ω	Часть пространства, которая является объединением всех лучей, выходящих из данной точки и пересекающих некоторую поверхность	стерадиан (ср)