Высота треугольника — Википедия
Материал из Википедии — свободной энциклопедии
Высота в треугольниках различного типа
Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону (точнее, на прямую, содержащую противоположную сторону). В зависимости от типа треугольника высота может содержаться внутри треугольника (для остроугольного треугольника), совпадать с его стороной (являться катетом прямоугольного треугольника) или проходить вне треугольника у тупоугольного треугольника.
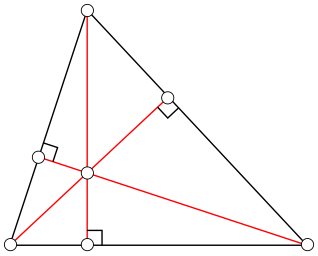Высоты треугольника- Все три высоты треугольника пересекаются в одной точке, называемой ортоцентром. Это утверждение легко доказать, используя векторное тождество, справедливое для любых точек A, B, C, E{\displaystyle A,\ B,\ C,\ E}, не обязательно даже лежащих в одной плоскости:
- EA→⋅BC→+EB→⋅CA→+EC→⋅AB→=0{\displaystyle {\overrightarrow {EA}}\cdot {\overrightarrow {BC}}+{\overrightarrow {EB}}\cdot {\overrightarrow {CA}}+{\overrightarrow {EC}}\cdot {\overrightarrow {AB}}=0}
(Для доказательства тождества следует воспользоваться формулами
- AB→=EB→−EA→,BC→=EC→−EB→,CA→=EA→−EC→{\displaystyle {\overrightarrow {AB}}={\overrightarrow {EB}}-{\overrightarrow {EA}},\,{\overrightarrow {BC}}={\overrightarrow {EC}}-{\overrightarrow {EB}},\,{\overrightarrow {CA}}={\overrightarrow {EA}}-{\overrightarrow {EC}}}
В качестве точки E следует взять пересечение двух высот треугольника.)
- Ортоцентр изогонально сопряжен центру описанной окружности.
- Ортоцентр лежит на одной прямой с центроидом, центром
- Ортоцентр остроугольного треугольника является центром окружности, вписанной в его ортотреугольник.
- Центр описанной около треугольника окружности служит ортоцентром треугольника с вершинами в серединах сторон данного треугольника. Последний треугольник называют дополнительным треугольником по отношению к первому треугольнику.
- Последнее свойство можно сформулировать так: Центр описанной около треугольника окружности служит ортоцентром дополнительного треугольника.
- Точки, симметричные ортоцентру треугольника относительно его сторон, лежат на описанной окружности.
- Точки, симметричные ортоцентру треугольника относительно середин сторон, также лежат на описанной окружности и совпадают с точками, диаметрально противоположными соответствующим вершинам.
- Если О — центр описанной окружности ΔABC, то OH→=OA→+OB→+OC→{\displaystyle {\overrightarrow {OH}}={\overrightarrow {OA}}+{\overrightarrow {OB}}+{\overrightarrow {OC}}} ,
- |OH|=9R2−(a2+b2+c2){\displaystyle |OH|={\sqrt {9R^{2}-(a^{2}+b^{2}+c^{2})}}} , где R{\displaystyle R} — радиус описанной окружности; a,b,c{\displaystyle a,b,c} — длины сторон треугольника.
- Расстояние от вершины треугольника до ортоцентра вдвое больше, чем расстояние от центра описанной окружности до противоположной стороны.
- Любой отрезок, проведенный из ортоцентра до пересечения с описанной окружностью всегда делится окружностью Эйлера пополам. Ортоцентр есть центр гомотетии этих двух окружностей.
- Теорема Гамильтона. Три отрезка прямых, соединяющих ортоцентр с вершинами остроугольного треугольника, разбивают его на три треугольника, имеющих ту же самую окружность Эйлера (окружность девяти точек), что и исходный остроугольный треугольник.
- Следствия теоремы Гамильтона:
- Три отрезка прямых, соединяющих ортоцентр с вершинами остроугольного треугольника, разбивают его на три треугольника Гамильтона, имеющих равные радиусы описанных окружностей.
- Радиусы описанных окружностей трёх треугольников Гамильтона равны радиусу окружности, описанной около исходного остроугольного треугольника.
- В остроугольном треугольнике ортоцентр лежит внутри треугольника; в тупоугольном — вне треугольника; в прямоугольном — в вершине прямого угла.
Свойства высот равнобедренного треугольника[править | править код]
- Если в треугольнике две высоты равны, то треугольник — равнобедренный (теорема Штейнера — Лемуса), и третья высота одновременно является медианой и биссектрисой того угла, из которого она выходит.
- Верно и обратное: в равнобедренном треугольнике две высоты равны, а третья высота одновременно является медианой и биссектрисой.
- У равностороннего треугольника все три высоты равны.
Свойства оснований высот треугольника[править | править код]
- Основания высот образуют так называемый ортотреугольник, обладающий собственными свойствами.
- Описанная около ортотреугольника окружность — окружность Эйлера. На этой окружности также лежат три середины сторон треугольника и три середины трёх отрезков, соединяющих ортоцентр с вершинами треугольника.
- Другая формулировка последнего свойства:
- Теорема Эйлера для окружности девяти точек. Основания трёх высот произвольного треугольника, середины трёх его сторон (основания его внутренних медиан) и середины трёх отрезков, соединяющих его вершины с ортоцентром, все лежат на одной окружности (на окружности девяти точек).
- Теорема. В любом треугольнике отрезок, соединяющий основания двух высот треугольника, отсекает треугольник подобный данному.
- Теорема. В треугольнике отрезок, соединяющий основания двух высот треугольника, лежащие на двух сторонах, антипараллелен третьей стороне, с которой он не имеет общих точек. Через два его конца, а также через две вершины третьей упомянутой стороны всегда можно провести окружность.
Свойства минимальной из высот треугольника[править | править код]
Минимальная из высот треугольника обладает многими экстремальными свойствами. Например:
- Минимальная ортогональная проекция треугольника на прямые, лежащие в плоскости треугольника, имеет длину, равную наименьшей из его высот.
- Минимальный прямолинейный разрез в плоскости, через который можно протащить несгибаемую треугольную пластину, должен иметь длину, равную наименьшей из высот этой пластины.
- При непрерывном движении двух точек по периметру треугольника друг навстречу другу, максимальное расстояние между ними за время движения от первой встречи до второй, не может быть меньше длины наименьшей из высот треугольника.
- Минимальная высота в треугольнике всегда проходит внутри этого треугольника.
- ha=bsinγ=csinβ,{\displaystyle h_{a}=b\sin \gamma =c\sin \beta ,}
- ha=2Sa,{\displaystyle h_{a}={\frac {2S}{a}},} где S{\displaystyle S} — площадь треугольника, a{\displaystyle a} — длина стороны треугольника, на которую опущена высота.
- ha2=12(b2+c2−12(a2+(b2−c2)2a2)){\displaystyle h_{a}^{2}={\frac {1}{2}}(b^{2}+c^{2}-{\frac {1}{2}}(a^{2}+{\frac {(b^{2}-c^{2})^{2}}{a^{2}}}))}
- ha=bc2R,{\displaystyle h_{a}={\frac {bc}{2R}},} где bc{\displaystyle bc} — произведение боковых сторон, R−{\displaystyle R-} радиус описанной окружности
- ha:hb:hc=1a:1b:1c=bc:ac:ab{\displaystyle h_{a}:h_{b}:h_{c}={\frac {1}{a}}:{\frac {1}{b}}:{\frac {1}{c}}=bc:ac:ab}
- 1ha+1hb+1hc=1r{\displaystyle {\frac {1}{h_{a}}}+{\frac {1}{h_{b}}}+{\frac {1}{h_{c}}}={\frac {1}{r}}}, где r{\displaystyle r} — радиус вписанной окружности.
- S=1(1ha+1hb+1hc)⋅(1ha+1hb−1hc)⋅(1ha+1hc−1hb)⋅(1hb+1hc−1ha){\displaystyle S={\frac {1}{\sqrt {({\frac {1}{h_{a}}}+{\frac {1}{h_{b}}}+{\frac {1}{h_{c}}}){\cdot }({\frac {1}{h_{a}}}+{\frac {1}{h_{b}}}-{\frac {1}{h_{c}}}){\cdot }({\frac {1}{h_{a}}}+{\frac {1}{h_{c}}}-{\frac {1}{h_{b}}}){\cdot }({\frac {1}{h_{b}}}+{\frac {1}{h_{c}}}-{\frac {1}{h_{a}}})}}}}, где S{\displaystyle S} — площадь треугольника.
- a=2ha⋅(1ha+1hb+1hc)⋅(1ha+1hb−1hc)⋅(1ha+1hc−1hb)⋅(1hb+1hc−1ha){\displaystyle a={\frac {2}{h_{a}{\cdot }{\sqrt {({\frac {1}{h_{a}}}+{\frac {1}{h_{b}}}+{\frac {1}{h_{c}}}){\cdot }({\frac {1}{h_{a}}}+{\frac {1}{h_{b}}}-{\frac {1}{h_{c}}}){\cdot }({\frac {1}{h_{a}}}+{\frac {1}{h_{c}}}-{\frac {1}{h_{b}}}){\cdot }({\frac {1}{h_{b}}}+{\frac {1}{h_{c}}}-{\frac {1}{h_{a}}})}}}}}, a{\displaystyle a} — сторона треугольника к которой опускается высота ha{\displaystyle h_{a}}.
- Высота равнобедренного треугольника, опущенная на основание:
- hc=124a2−c2,{\displaystyle h_{c}={\frac {1}{2}}{\sqrt {4a^{2}-c^{2}}},}
- где c{\displaystyle c} — основание, a{\displaystyle a} — боковая сторона.
- h=32a{\displaystyle h={\frac {\sqrt {3}}{2}}a} — высота в равностороннем треугольнике со стороной a{\displaystyle a}.
Теорема о высоте прямоугольного треугольника[править | править код]
Если высота в прямоугольном треугольнике ABC{\displaystyle ABC} длиной h{\displaystyle h}, проведённая из вершины прямого угла, делит гипотенузу длиной c{\displaystyle c} на отрезки m{\displaystyle m} и n{\displaystyle n}, соответствующие катетам b{\displaystyle b} и a{\displaystyle a}, то верны следующие равенства:
- h3=mn{\displaystyle h^{2}=mn}
- a2=cn{\displaystyle a^{2}=cn}; b2=cm{\displaystyle b^{2}=cm}
- ch=ab{\displaystyle ch=ab}
См. с. 51, ф. (1.11-4)[2]. Теорема о проекциях: c=acosβ+bcosα; a=bcosγ+ccosβ; b=ccosα+acosγ{\displaystyle c=a\cos \beta +b\cos \alpha ;\ a=b\cos \gamma +c\cos \beta ;\ b=c\cos \alpha +a\cos \gamma }. Из теоремы о проекциях следует то, что высота, опущенная, например, из вершины C{\displaystyle C}, делит противоположную ей сторону c{\displaystyle c} на две части acosβ{\displaystyle a\cos \beta } и bcosα{\displaystyle b\cos \alpha }, считая от вершины A{\displaystyle A} к B{\displaystyle B}.
Высота похожа на кота,
Который, выгнув спину,
И под прямым углом
Соединит вершину
И сторону хвостом.[3]
Теорема[4]. Пусть ABCD{\displaystyle ABCD} – вписанный четырёхугольник, A1{\displaystyle A_{1}} – основание перпендикуляра (высоты), опущенного из вершины A{\displaystyle A} на диагональ BD{\displaystyle BD}; аналогично определяются точки B1,C1,D1{\displaystyle B_{1},C_{1},D_{1}}. Тогда точки A1,B1,C1,D1{\displaystyle A_{1},B_{1},C_{1},D_{1}} лежат на одной окружности.
- ↑ Зетель С.И. Новая геометрия треугольника. Пособие для учителей. 2-е издание.. — М.: Учпедгиз, 1962. — С. 137-138, п. 126, теорема, следствия.
- ↑ Корн Г.А., Корн Т.М. Справочник по математике для научных работников и инженеров. — М.: «Наука», 1974. — 832 с.
- ↑ Сафронова Вера Николаевна,. Урок геометрии в 7-м классе по теме: «Медиана, биссектриса, высота» (рус.). Открытый урок. Издательский дом «Первое сентября». Дата обращения 19 июля 2017.
- ↑ Вокруг задачи Архимеда. Упр. 7, рис. 11, следствие, c. 5.
Высота (геометрия) — это… Что такое Высота (геометрия)?
Высота в элементарной геометрии — отрезок перпендикуляра, опущенного из вершины геометрической фигуры (например, треугольника, пирамиды, конуса) на её основание или на продолжение основания. Под высотой также подразумевается длина этого отрезка.
Высота трапеции, призмы, цилиндра, шарового слоя, усеченных параллельно основанию — расстояние между верхним и нижним основаниями.
Высота треугольника
Высота треугольника — отрезок, опущенный из вершины треугольника перпендикулярно противоположной стороне.
Все высоты треугольника пересекаются в одной точке, называемой ортоцентром этого треугольника. — Эту теорему легко доказать, используя векторное тождество, справедливое для любых точек A, B, C, E, не обязательно даже лежащих в одной плоскости:
(Для доказательства следует взять в качестве точки E пересечение двух высот треугольника.)
Площадь треугольника равна половине произведения высоты треугольника на соответствующее основание. Кроме формулы, удобной для расчёта площади, из этого также следует, что длины высот треугольника обратно пропорциональны длинам соответствующих сторон.
Минимальная из высот треугольника обладает многими экстремальными свойствами. Например:
1. Минимальная ортогональная проекция треугольника на прямую, лежащую в плоскости треугольника, имеет длину, равную наименьшей из его высот.
2. Минимальный прямолинейный разрез в плоскости, через который можно протащить несгибаемую треугольную пластину, должен иметь длину, равную наименьшей из высот этой пластины.
3. При непрерывном движении двух точек по периметру треугольника друг навстречу другу, если они встречаются хотя бы дважды, тогда максимальное расстояние между точками во время их движения не может быть меньше длины наименьшей из высот треугольника.
Высота — Математическая энциклопедия
В элементарной геометрии — отрезок перпендикуляра, опущенного из вершины гео-метрич. фигуры (напр., треугольника, пирамиды, конуса) на ее основание или на продолжение основания, а также длина этого отрезка. В. трапеции, призмы, цилиндра, шарового слоя, усеченных параллельно основанию пирамиды и конуса,- расстояние между верхним и нижним основаниями. На рис. изображены В. (ft) треугольников, трапеции и усеченного конуса. БСЭ-3.
Источник: Математическая энциклопедия на Gufo.me
Значения в других словарях
- высота — -ы, мн. высоты, ж. 1. Протяженность по вертикали снизу вверх; вышина. Высота здания двадцать метров. Высота мачты. □ Река, разрезающая прибой, образует здесь несколько длинных, очень крутых валов. — Сами же валы достигают высоты нескольких метров. Малый академический словарь
- высота — Высота, высоты, высоты, высот, высоте, высотам, высоту, высоты, высотой, высотою, высотами, высоте, высотах Грамматический словарь Зализняка
- ВЫСОТА — ВЫСОТА — в геометрии — отрезок перпендикуляра, опущенного из вершины геометрической фигуры (напр., треугольника, пирамиды, конуса) на ее основание (или продолжение основания) — а также длина этого отрезка. Большой энциклопедический словарь
- высота — сущ., ж., употр. часто (нет) чего? высоты, чему? высоте, (вижу) что? высоту, чем? высотой, о чём? о высоте; мн. что? высоты, (нет) чего? высот, чему? высотам, (вижу) что? высоты, чем? высотами, о чём? о высотах… Толковый словарь Дмитриева
- Высота — (евр. бамот, ед.ч. бама). I. Языч. капище хананеев (Чис 33:52) или моавитян (Чис 21:28; 22:41; Иер 48:35). Израильтянам было приказано истреблять… Библейская энциклопедия Брокгауза
- высота — ВЫСОТА -ы; мн. высоты; ж. 1. Величина, протяжённость чего-л. от нижней точки до верхней, снизу вверх. В. дома, дерева, горы. В. волны. Плотина высотой в сто пятьдесят метров. Измерить, определить высоту чего-л. 2. Расстояние от какой-л. Толковый словарь Кузнецова
- высота — ВЫСОТ’А, высоты, мн. высоты, высот, ·жен. 1. только ед. Протяжение снизу вверх, вышина. Высота дома. Башня большой высоты. | (мн. только спец. научн.). Расстояние от земной поверхности, измеряемое по вертикальной линии снизу вверх. Толковый словарь Ушакова
- высота — Выс/от/а́. Морфемно-орфографический словарь
- высота — ВЫСОТА — высота барьера. Вертикальный размер барьера, который различен для мужчин, женщин, юношей и девушек, а также на различных дистанциях барьерного бега. — квалификационная высота. Словарь спортивных терминов
- высота — Быть, оказаться на высоте чего или на высоте положения — удовлетворять самым строгим требованиям чего-н. ► Артисты были на высоте положения. Фразеологический словарь Волковой
- высота — орф. высота, -ы, мн. -оты, -от Орфографический словарь Лопатина
- Высота — I Высота́ небесного светила, угол между направлением на светило и плоскостью истинного горизонта; см. Небесные координаты. II Высота́ в геометрии, отрезок перпендикуляра, опущенного из вершины геометрической фигуры (например, треугольника, пирамиды… Большая советская энциклопедия
- высота — ВОЗВЫШЕННОСТЬ — НИЗМЕННОСТЬ Холмистая возвышенность — болотистая низменность. ○ Обширная Западно-Сибирская низменность имеет слабый наклон к северу … . Возвышенности имеют разную форму и располагаются изолированно, группами или образуют гряды. Словарь антонимов русского языка
- высота — сущ., кол-во синонимов… Словарь синонимов русского языка
- высота — ВЫСОТА, высотина и пр. см. высокий. Также см. высокий Толковый словарь Даля
- высота — • абсолютная ~ • безмерная ~ • беспредельная ~ • большая ~ • головокружительная ~ • значительная ~ • максимальная ~ • небывалая ~ • невиданная ~ • необыкновенная ~ • огромная ~ • рекордная ~ • страшная ~ Словарь русской идиоматики
- высота — см.: вес; Лучше нет красоты… Толковый словарь русского арго
- ВЫСОТА — • ВЫСОТА, в астрономии — угловое расстояние от небесного тела до горизонта наблюдателя. Измеряется в градусах от 0 (на линии горизонта) до 90 (в зените) по БОЛЬШОМУ КРУГУ, проходящему через данное тело и зенит. Научно-технический словарь
- высота — • Бездонная (Бальмонт). • Безмерная (Муйжель). • Бесстрастная (Голен.-Кутузов). • Гордая (Бальмонт). • Лазурная (Городецкий, Круглов). • Надзвездная (Льдов). • Недоступная (Бальмонт). • Недосягаемая (Гиппиус). • Непобедимая (Белый). • Неприступная (Брюсов). • Немая (Ратгауз). • Холодная (Бальмонт). Словарь литературных эпитетов
- высота — ВЫСОТА, ы, мн. оты, от, отам, ж. 1. Величина, протяжённость чего-н. от нижней точки до верхней. В. кирпичной кладки. В. прибоя. В. циклона. 2. Пространство, расстояние от земли вверх. Смотреть в высоту. Самолёт набирает высоту. Лететь на большой высоте. Толковый словарь Ожегова
- высота — Высь, вышина, подъем, уровень, градус Вода поднялась выше ординара ср. !! степень, гора см. >> достоинство, степень см. также -> быть на высоте своего положения Словарь синонимов Абрамова
ВЫСОТА — это… Что такое ВЫСОТА?
ВЫСОТА — ВЫСОТА, высоты, мн. высоты, высот, жен. 1. только ед. Протяжение снизу вверх, вышина. Высота дома. Башня большой высоты. || (мн. только спец. научн.). Расстояние от земной поверхности, измеряемое по вертикальной линии снизу вверх. Аэроплан летал… … Толковый словарь Ушакова
высота — ВЫСОТА1, ы, мн высоты, м То же, что возвышенность. Охотничью избушку решили ставить на высоте прямо над обрывом. ВЫСОТА2, ы, мн оты, от, отам, ж, чего. Перен. О высоком уровне развития, совершенствования чего л.; Син.: вершина. Высоты мастерства … Толковый словарь русских существительных
высота — Высь, вышина, подъем, уровень, градус. Вода поднялась выше ординара.. Ср. . См. достоинство, степень быть на высоте своего положения… .. Словарь русских синонимов и сходных по смыслу выражений. под. ред. Н. Абрамова, М.: Русские словари, 1999.… … Словарь синонимов
ВЫСОТА — • ВЫСОТА, в астрономии угловое расстояние от небесного тела до горизонта наблюдателя. Измеряется в градусах от 0 (на линии горизонта) до 90 (в зените) по БОЛЬШОМУ КРУГУ, проходящему через данное тело и зенит. Если объект расположен ниже горизонта … Научно-технический энциклопедический словарь
высота — ы; мн. высоты; ж. 1. Величина, протяжённость чего л. от нижней точки до верхней, снизу вверх. В. дома, дерева, горы. В. волны. Плотина высотой в сто пятьдесят метров. Измерить, определить высоту чего л. 2. Расстояние от какой л. поверхности до… … Энциклопедический словарь
Высота 88,5 — Жанр агитпропфильм Режиссёр Юрий Тарич Автор сценария Ю. Берман Б. Верховский В главных ролях … Википедия
Высота 88 — Высота 88,5 (фильм, 1932) Высота 88,5 Жанр агитпропфильм Режиссёр Юрий Тарич Автор сценария Ю.Берман, Б.Верховский В главных ролях Иван Клюквин … Википедия
высота — сущ., ж., употр. часто Морфология: (нет) чего? высоты, чему? высоте, (вижу) что? высоту, чем? высотой, о чём? о высоте; мн. что? высоты, (нет) чего? высот, чему? высотам, (вижу) что? высоты, чем? высотами, о чём? о высотах 1. Высотой какого либо… … Толковый словарь Дмитриева
ВЫСОТА — в геометрии отрезок перпендикуляра, опущенного из вершины геометрической фигуры (напр., треугольника, пирамиды, конуса) на ее основание (или продолжение основания), а также длина этого отрезка. Высота призмы, цилиндра, шарового слоя, а также… … Большой Энциклопедический словарь
ВЫСОТА — ВЫСОТА, высотина и пр. см. высокий. Толковый словарь Даля. В.И. Даль. 1863 1866 … Толковый словарь Даля
ВЫСОТА (в геометрии) — это… Что такое ВЫСОТА (в геометрии)?
- ВЫСОТА (в геометрии)
- ВЫСОТА (в геометрии)
ВЫСОТА́, в геометрии — отрезок перпендикуляра, опущенного из вершины геометрической фигуры (напр., треугольника, пирамиды, конуса) на ее основание (или продолжение основания), а также длина этого отрезка. Высота призмы, цилиндра, шарового слоя, а также усеченных параллельно основанию пирамиды и конуса — расстояние между верхними и нижними основаниями.
Энциклопедический словарь. 2009.
- ВЫСОТА (в астрономии)
- ВЫСОЦКИЙ Михаил Иосифович
Смотреть что такое «ВЫСОТА (в геометрии)» в других словарях:
ВЫСОТА — в геометрии отрезок перпендикуляра, опущенного из вершины геометрической фигуры (напр., треугольника, пирамиды, конуса) на ее основание (или продолжение основания), а также длина этого отрезка. Высота призмы, цилиндра, шарового слоя, а также… … Большой Энциклопедический словарь
Высота (геометрич.) — Высота в геометрии, отрезок перпендикуляра, опущенного из вершины геометрической фигуры (например, треугольника, пирамиды, конуса) на её основание или продолжение основания, а также длина этого отрезка. В. призмы, цилиндра, шарового слоя,… … Большая советская энциклопедия
Высота — I Высота небесного светила, угол между направлением на светило и плоскостью истинного горизонта; см. Небесные координаты. II Высота в геометрии, отрезок перпендикуляра, опущенного из вершины геометрической фигуры (например,… … Большая советская энциклопедия
ВЫСОТА — 1) ВЫСОТА в астрономии см. Небесные координаты. 2) ВЫСОТА в геометрии отрезок перпендикуляра, опущенного из вершины геом. фигуры (напр., треугольника, трапеции, пирамиды, конуса) на её основание (или продолжение основания), а также длина этого… … Большой энциклопедический политехнический словарь
Высота (значения) — Высота размер или расстояние в вертикальном направлении. Другие значения: В астрономии: Высота светила угол между плоскостью математического горизонта и направлением на светило. В военном деле: Высота возвышенность рельефа. В… … Википедия
ВЫСОТА — (1) в геометрии а) плоской фигуры наибольший из перпендикуляров, опущенных из точек контура фигуры на её основание или его продолжение; б) пространственной фигуры наибольший из перпендикуляров, опущенных из граничных точек этой фигуры на… … Большая политехническая энциклопедия
высота — 3.4 высота (height): Размер самой короткой кромки карты. Источник: ГОСТ Р ИСО/МЭК 15457 1 2006: Карты идентификационные. Карты тонкие гибкие. Часть 1. Физические характеристики … Словарь-справочник терминов нормативно-технической документации
высота здания — 3.1 высота здания : Высота здания определяется высотой расположения верхнего этажа, не считая верхнего технического этажа, а высота расположения этажа определяется разностью отметок поверхности проезда для пожарных машин и нижней границы… … Словарь-справочник терминов нормативно-технической документации
Высота (геометрия) — У этого термина существуют и другие значения, см. Высота (значения). Высота в элементарной геометрии отрезок перпендикуляра, опущенного из вершины геометрической фигуры (например, треугольника, пирамиды, конуса) на её основание или на… … Википедия
ВЫСОТА — в диофантовой геометрии некоторая численная функция на множестве решений диофантова уравнения. В простейшем случае целочисленного решения диофантова уравнения высота есть функция решения, равная В таком виде она встречается уже в методе спуска… … Математическая энциклопедия
Высота (геометрия) | Наука | Fandom
Высота в элементарной геометрии — отрезок перпендикуляра, опущенного из вершины геометрической фигуры (например, треугольника, пирамиды, конуса) на её основание или на продолжение основания. Под высотой также подразумевается длина этого отрезка.
Высота трапеции, призмы, цилиндра, шарового слоя, усеченных параллельно основанию — расстояние между верхним и нижним основаниями.
Высота треугольника Править
Высота треугольника — отрезок, опущенный из вершины треугольника перпендикулярно противоположной стороне.
Все высоты треугольника пересекаются в одной точке, называемой ортоцентром этого треугольника. — Эту теорему легко доказать, используя векторное тождество, справедливое для любых точек A, B, C, E, не обязательно даже лежащих в одной плоскости:
- $ \overrightarrow{EA}\cdot\overrightarrow{BC} + \overrightarrow{EB}\cdot\overrightarrow{CA} + \overrightarrow{EC}\cdot\overrightarrow{AB} = 0 $
(Для доказательства следует взять в качестве точки E пересечение двух высот треугольника.)
Площадь треугольника равна половине произведения высоты треугольника на соответствующее основание. Кроме формулы, удобной для расчёта площади, из этого также следует, что длины высот треугольника обратно пропорциональны длинам соответствующих сторон.
Минимальная из высот треугольника обладает многими экстремальными свойствами. Например:
1. Минимальная ортогональная проекция треугольника на прямую, лежащую в плоскости треугольника, имеет длину, равную наименьшей из его высот.
2. Минимальный прямолинейный разрез в плоскости, через который можно протащить несгибаемую треугольную пластину, должен иметь длину, равную наименьшей из высот этой пластины.
3. При непрерывном движении двух точек по периметру треугольника друг навстречу другу, если они встречаются хотя бы дважды, тогда максимальное расстояние между точками во время их движения не может быть меньше длины наименьшей из высот треугольника.
Что такое высота?
В общем смысле высота – это расстояние от нижней до верхней точки, измеряемое по вертикальной линии снизу вверх. Однако данный термин имеет и другие значения. В этой статье расскажем о том, что такое высота в различных сферах науки и жизни.
Высота в повседневной жизни
В повседневной жизни мы привыкли использовать слово высота в значении, как мы уже упоминали, расстояния от нижней до верхней точки какой-либо поверхности или плоскости. Расстояние это, надо сказать, может быть не только физическим. Так, например, высота стены – это вполне ощутимая величина, а вот фраза «добиться высот в своем деле» имеет несколько иную природу, хотя, говоря эту фразу, мы все же имеем в виду расстояние, которое прошел человек на пути от новичка к профессионалу, хоть это расстояние и нельзя пощупать и измерить. В данном случае высота имеет значение высокого уровня развития.
Также высотой могут называть возвышенной место.
Высота в математике
Термин «высота» мы зачастую слышим в геометрии, высота фигуры – одна из самых важных ее параметров. Высота фигуры – это перпендикуляр, опущенный из вершины фигуры к ее основанию.
Высота геометрической фигуры зачастую используется в формулах для вычисления ее площади. Так, например, чтобы найти площадь треугольника, необходимо умножить высоту на основание и поделить полученное произведение пополам.
О том, как определить высоту треугольника, читайте в статье Как найти высоту треугольника.
Высота в физике
В физике высота – это одно из базовых свойств звука. Высота звука определяется частотой его воздействия на барабанную перепонку – чем больше частота колебаний, тем выше звук.
Интересно, что количественная оценка высоты звука базируется на статистической обработке огромного числа данных о субъективном восприятии звучания.
Высота в географии
В географии различают понятия абсолютной и относительной высоты.
Абсолютная высота (альтитуда) — это расстояние от конкретной точки земной поверхности до среднего уровня поверхности океана. Абсолютная высота – третья координата точки на земной поверхности, дополняющая широту и долготу и дающая максимально полное представление о расположении объекта. Если абсолютная высота лежит выше среднего уровня океана, она считается положительной, в противном случае высота называется отрицательной.
Относительная высота отсчитывается от условного уровня, который в конкретном случае требуется принять за нулевой.
Для определения высот объектов в географии используется прибор, который называется нивелир, а сама процедура измерения — нивелированием.
Высота полета
Высота полета – это расстояние от определенного уровня отсчета до воздушного судна, измеряемое по вертикали. Высота полета бывает относительной, истинной и абсолютной.
Относительная высота полета отсчитывается от уровня аэродрома, наивысшей точки рельефа или любой другой точки, выбранной за точку отсчета из неких соображений. Истинная высота определяется от точки, расположенной непосредственно под корпусом воздушного судна. Абсолютная высота измеряется от уровня океана.