Как начертить уклоны и конусность
Во многих деталях машин используются уклоны и конусность. Уклоны встречаются в профилях прокатной стали, в крановых рельсах, в косых шайбах и т. д. Конусности встречаются в центрах бабок токарных и других станков, на концах валов и ряда других деталей.
Уклон характеризует отклонение прямой линии от горизонтального или вертикального направлений. Для того чтобы построить уклон 1:1, на сторонах прямого угла откладывают произвольные, но равные величины (рис. 1). Очевидно, что уклон 1:1 соответствует углу в 45 градусов. Чтобы построить линию с уклоном 1:2, по горизонтали откладывают две единицы, для уклона 1:3 — три единицы и т. д. Как видно из чертежа, уклон есть отношение катета противолежащего к катету прилежащему, т. е. он выражается тангенсом угла а. Величину уклона на чертеже в соответствии с ГОСТ 2.307—68 указывают с помощью линии-выноски, на полке которой наносят знак уклона и его величину. Расположение знака уклона должно соответствовать определяемой линии: одна из прямых знака должна быть горизонтальна, другая — наклонена примерно под углом 30° в ту же сторону, как и сама линия уклона.
На рисунке в качестве примера построен профиль несимметричного двутавра, правая полка которого имеет уклон 1:16. Для ее построения находят точку А с помощью заданных размеров 26 и 10. В стороне строят линию с уклоном 1:16, для чего по вертикали откладывают, например, 5 мм, а по горизонтали 80 мм; проводят гипотенузу, направление которой определяет искомый уклон. С помощью рейсшины и угольника через точку А проводят линию уклона, параллельную гипотенузе.
Конусностью называют отношение диаметра основания конуса к его высоте. В этом случае конусность К=d/l. Для усеченного конуса
n
n
TBegin—>TEnd—>
n
n
Рис. 1. Построение уклонов
n
n
Перед размерным числом, характеризующим конусность, наносят условный знак в виде равнобедренного треугольника, вершину которого направляют в сторону вершины самого конуса. Знак конусности располагают параллельно оси конуса над осью или на полке линии-выноски, заканчивающейся стрелкой, как в случае надписи уклона. Конусность выбирают в соответствии с ГОСТ 8593—57 .
n
n
n
n
Рис. 2. Пример построения уклонов
n
n
TBegin—>TEnd—>
n
n
Рис. 3. Построение конусности
n
Нормальные конусности и углы
Источник: ГОСТ 8593-81
Конусность К есть отношение разности диаметров двух поперечных сечений конуса к расстоянию между ними.
Уклон «i» есть отношение разности размеров двух поперечных сечений к расстоянию между ними.
Таблица 1. Углы конусности
|
Конусность К |
Угол конуса 2а |
Угол уклона а |
Исходное значение (К или 2а) |
|
1:200 |
0°7’11» |
0°8’36» |
1:200 |
|
1:100 |
0°34’23» |
0°17’11» |
1:100 |
|
1:50 |
1°8’46» |
0°34’23» |
1:50 |
|
|
1°54’35» |
0°57’17» |
1:30 |
|
1:20 |
2°51’51» |
1°25’56» |
1:20 |
|
1:15 |
3°49’6″ |
1°54’33» |
1:15 |
|
1:12 |
4°46’19» |
2°23’9″ |
1:12 |
|
1:10 |
5°43’29» |
2°51’45» |
1:10 |
|
1:8 |
7°9’10» |
3°34’35» |
1:8 |
|
1:7 |
8°10’16» |
4°5’8″ |
1:7 |
|
1:5 |
11°25’16» |
5°42’38» |
1:5 |
|
1:3 |
18°55’29» |
9°27’44» |
1:3 |
|
1:1,866 |
|
15° |
30° |
|
1:1,207 |
45° |
22°30′ |
45° |
|
1:0,866 |
60° |
30° |
|
|
1:0,652 |
75° |
37°30′ |
75° |
|
1:0,500 |
90° |
45° |
90° |
|
1:0,289 |
120° |
60° |
120° |
К оглавлению
Конусность — Википедия
Материал из Википедии — свободной энциклопедии
а — полный конус.б — усеченный конус.
В качестве примера приведено условное обозначение конусности по ГОСТ 2.307-68.
Конусность (C) — отношение диаметра окружности (D) основания конуса к его высоте (H) для полных конусов или отношение разности диаметров двух торцевых поперечных сечений конуса (D и d) к расстоянию между ними (L) для усеченных конусов. Конусность, как правило, выражается в отношении двух чисел например конусность 1:10 означает что высота полного конуса в 10 раз больше диаметра основания.
C=DH=D−dL{\displaystyle C={\frac {D}{H}}={\frac {D-d}{L}}}Также конусность может задаваться углом вершины конуса (α). Половина угла вершины конуса называется уклоном конуса (α/2).
C=2tg(α/2){\displaystyle C=2tg(\alpha /2)}В некоторых странах (в основном это страны с распространенной имперской системой длины) конусность задают в виде диаметра основания конуса единичной высоты. Например 0,6 дюйма на фут или 0,05 дюйма на дюйм, что соответствует конусности 1:20.
Конусность может задаваться в процентах и промилле.
ГОСТ Р 53440-2009 (ГОСТ 8593-81 утратил силу на территории РФ с 01.01.2012) предусматривает следующие конусности:
1:500, 1:200, 1:100, 1:50, 1:30, 1:20, 1:15, 1:12, 1:10, 1:8, 1:7, 1:6, 1:5, 1:4, 1:3, 30°, 45°, 60°, 75°, 90°, 120°
| Конусность | Угловая конусность | Уклон конуса |
|---|---|---|
| 1:200 | 0° 17’ 12” | 0° 8’ 36” |
| 1:100 | 0° 34’ 23” | 0° 17’ 11” |
| 1:50 | 1° 8’ 45” | 0° 34’ 23” |
| 1:30 | 1° 54’ 35” | 0° 57’ 17” |
| 1:20 | 2° 51’ 51” | 1° 25’ 56” |
| 1:15 | 3° 49’ 6” | 1° 54’ 33” |
| 1:12 | 4° 46’ 19” | 2° 23’ 9” |
| 1:10 | 5° 43’ 29” | 2° 51’ 45” |
| 1:8 | 7° 9’ 10” | 3° 34’ 35” |
| 1:7 | 8° 10’ 16” | 4° 5’ 8” |
| 1:5 | 11° 25’ 16” | 5° 42’ 38” |
| 1:4 | 14° 15’ 0” | 7° 7’ 30” |
| 1:3 | 18° 55’ 29” | 9° 27’ 44” |
| 1:1,866 | 30° | 15° |
| 1:1,207 | 45° | 22° 30’ |
| 1:0,866 | 60° | 30° |
| 1:0,652 | 75° | 37° 30’ |
| 1:0,500 | 90° | 45° |
| 1:0,289 | 120° | 60° |
Конусность 1 4 означает что
1) Одной единице, а другого четырём единицам;
2) Двум единицам, а другого восьми единицам;
3) Одной единице, а другого пяти единицам.
Какие проставляются размеры при выполнении чертежа в масштабе, отличном от 1:1?
1) Увеличение в два раза;
2) Уменьшение в четыре раза;
3) Независимо от масштаба изображения ставятся действительные размеры изделия;
Конусность 1:4 означает, что?
1) Диаметр основания составляет 1 часть, а высота 4 части;
2) Диаметр основания составляет 1 часть, а высота 5 частей;
3) Диаметр составляет третью часть от высоты конуса.
На каком чертеже (см. Рис. СЗ-5) рационально нанесены величины радиусов, диаметров, толщины деталей и размеры, определяющие расположение отверстий?
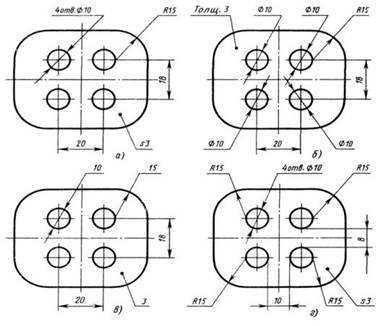
1) На третьем чертеже
2) На четвёртом чертеже
3) На первом чертеже
Точка может быть однозначно определена в пространстве, если она спроецирована?
1) На три плоскости проекций;
2) На одну плоскость проекций;
Формат А4 располагают :
2) Только вертикально
3) По горизонтали
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Для студента самое главное не сдать экзамен, а вовремя вспомнить про него. 9755 — 
| 7376 — 
или читать все.
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Иногда, в задачах по начертательной геометрии или работах по инженерной графике, или при выполнении других чертежей, требуется построить уклон и конус. В этой статье Вы узнаете о том, что такое уклон и конусность, как их построить, как правильно обозначить на чертеже.
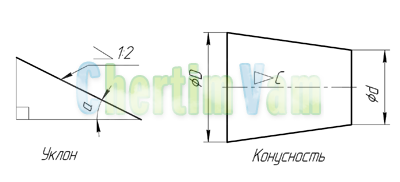
Что такое уклон? Как определить уклон? Как построить уклон? Обозначение уклона на чертежах по ГОСТ.
Уклон. Уклон это отклонение прямой линии от вертикального или горизонтального положения.
Определение уклона. Уклон определяется как отношение противолежащего катета угла прямоугольного треугольника к прилежащему катету, то есть он выражается тангенсом угла а. Уклон можно посчитать по формуле i=AC/AB=tga.
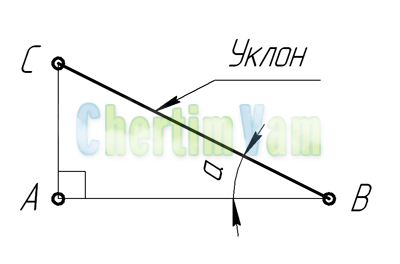
Построение уклона. На примере (рисунок ) наглядно продемонстрировано построение уклона. Для построения уклона 1:1, например, нужно на сторонах прямого угла отложить произвольные, но равные отрезки. Такой уклон, будет соответствовать углу в 45 градусов. Для того чтобы построить уклон 1:2, нужно по горизонтали отложить отрезок равный по значению двум отрезкам отложенным по вертикали. Как видно из чертежа, уклон есть отношение катета противолежащего к катету прилежащему, т. е. он выражается тангенсом угла а.
Обозначение уклона на чертежах. Обозначение уклонов на чертеже выполняется в соответствии с ГОСТ 2.307—68. На чертеже указывают величину уклона с помощью линии-выноски. На полке линии-выноски наносят знак и величину уклона. Знак уклона должен соответствовать уклону определяемой линии, то есть одна из прямых знака уклона должна быть горизонтальна, а другая должна быть наклонена в ту же сторону, что и определяемая линия уклона. Угол уклона линии знака примерно 30°.
Что такое конусность? Формула для расчёта конусности. Обозначение конусности на чертежах.
Конусность. Конусностью называется отношение диаметра основания конуса к высоте. Конусность рассчитывается по формуле К=D/h, где D – диаметр основания конуса, h – высота. Если конус усеченный, то конусность рассчитывается как отношение разности диаметров усеченного конуса к его высоте. В случае усечённого конуса, формула конусности будет иметь вид: К = (D-d)/h.
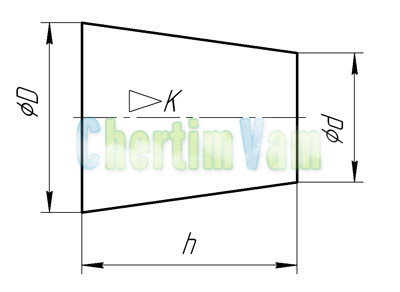
Обозначение конусности на чертежах. Форму и величину конуса определяют нанесением трех из перечисленных размеров: 1) диаметр большого основания D; 2) диаметр малого основания d; 3) диаметр в заданном поперечном сечении Ds , имеющем заданное осевое положение Ls; 4) длина конуса L; 5) угол конуса а; 6) конусность с . Также на чертеже допускается указывать и дополнительные размеры, как справочные.
Размеры стандартизованных конусов не нужно указывать на чертеже. Достаточно на чертеже привести условное обозначение конусности по соответствующему стандарту.
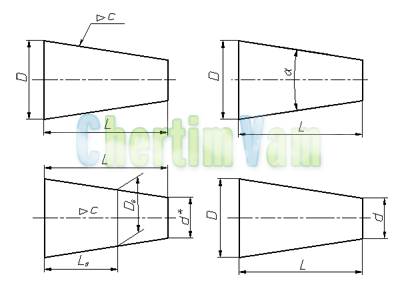
Конусность, как и уклон, может быть указана в градусах, дробью (простой, в виде отношения двух чисел или десятичной), в процентах.
Например, конусность 1:5 может быть также обозначена как отношение 1:5, 11°25’16», десятичной дробью 0,2 и в процентах 20.
Для конусов, которые применяются в машиностроении, OCT/BKC 7652 устанавливает ряд нормальных конусностей. Нормальные конусности — 1:3; 1:5; 1:8; 1:10; 1:15; 1:20; 1:30; 1:50; 1:100; 1:200. Также в могут быть использованы — 30, 45, 60, 75, 90 и 120°.
На изображениях конических элементов деталей размеры могут быть проставлены различно: диаметры большего и меньшего оснований усеченного конуса и его длина; угол наклона образующей (или угол конуса) или величина конусности и диаметр основания, длина и т.п.
Конусность
Отношение разности диаметров двух поперечных сечений конуса (D-d.) к расстоянию между ними (l) (рис. 6.39, а) называется конусностью (К): К = (D – d)/l.
Рис. 6.39. Построение конусности и нанесение се величины
Например, конический элемент детали с диаметром большего основания 25 мм, диаметром меньшего основания 15 мм, длиной 50 мм будет иметь конусность К = (D – d)/l = (25 – 15)/50 = 1/5 = 1:5.
При проектировании новых изделий применяются величины конусности, установленные ГОСТ 8593–81: 1:3; 1:5; 1:7; 1:8; 1:10; 1:12; 1:15; 1:20; 1:30. Стандартизированы также величины конусности, которые имеют элементы деталей с часто встречающимися углами между образующими конуса: углу 30° соответствует конусность 1:1,866; 45° – 1:1,207; 60° – 1:0,866; 75° – 1:0,652; углу 90° – 1:0,5. В чертежах металлорежущих инструментов часто конусность определяется надписью, указывающей номер конуса Морзе. В этих случаях размеры конических элементов устанавливают по ГОСТ 10079–71 и др.
На чертежах конусность наносят согласно правилам ГОСТ 2.307–2011. Перед размерным числом, определяющим величину конусности, наносят условный знак в виде равнобедренного треугольника, острие которого направлено в сторону вершины конуса.
Знак и цифры, указывающие величину конусности, располагают на чертежах параллельно геометрической оси конического элемента.
Они могут быть проставлены над осью (рис. 6.39, 6) или на полке (рис. 6.39, в). В последнем случае полка соединяется с образующей конуса с помощью линии выноски, заканчивающейся стрелкой.
Уклон
Плоские поверхности деталей, расположенные наклонно, обозначают на чертеже величиной уклона. Как подсчитать эту величину, покажем на примере. Клин, изображенный на рис. 6.40, я, имеет наклонную поверхность, уклон которой нужно определить. Из размера наибольшей высоты клина вычтем размер наименьшей высоты: 50 – 40 = 10 мм. Разность между этими величинами можно рассматривать как размер катета прямоугольного треугольника, образовавшегося после проведения на чертеже горизонтальной линии (рис. 6.40, б). Величиной уклона будет отношение размера меньшего катета к размеру горизонтальной линии. В данном случае нужно разделить 10 на 100. Величина уклона клина будет 1:10.
Рис. 6.40. Определение величины уклона
На чертеже уклоны указывают знаком и отношением двух чисел, например 1:50; 3:5.
Если требуется изобразить на чертеже поверхность определенного уклона, например 3:20, вычерчивают прямоугольный треугольник, у которого один из катетов составляет три единицы длины, а второй – 20 таких же единиц (рис. 6.41).
Рис. 6.41. Построение уклонов и нанесение их величин
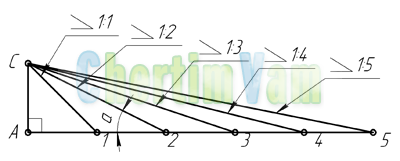
При вычерчивании деталей или при их разметке для построения линии по заданному уклону приходится проводить вспомогательные линии. Например, чтобы провести линию, уклон которой 1:4, через концевую точку вертикальной линии (рис. 6.42), отрезок прямой линии длиной 10 мм следует принять за единицу длины и отложить на продолжении горизонтальной линии четыре такие единицы (т.е. 40 мм). Затем через крайнее деление и верхнюю точку отрезка провести прямую линию.
Рис. 6.42. Построение линии по заданному уклону
Вершина знака уклона должна быть направлена в сторону наклона поверхности детали. Знак и размерное число располагают параллельно направлению, по отношению к которому задан уклон.
Обозначение уклона и конусности
Уклоны
Уклон, величина, характеризующая наклон одной прямой линии к другой. Выражают дробью или в %.
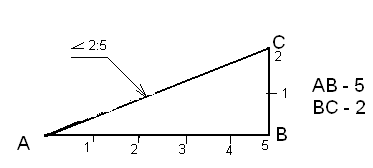
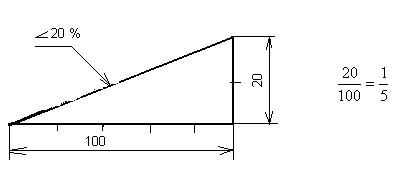
| — угол направлен в сторону уклона |
Рисунок 6.1
6.2 Конусность
Конусность ( С ) – это
отношение диаметра основания конуса к
его высоте. Для усеченного конуса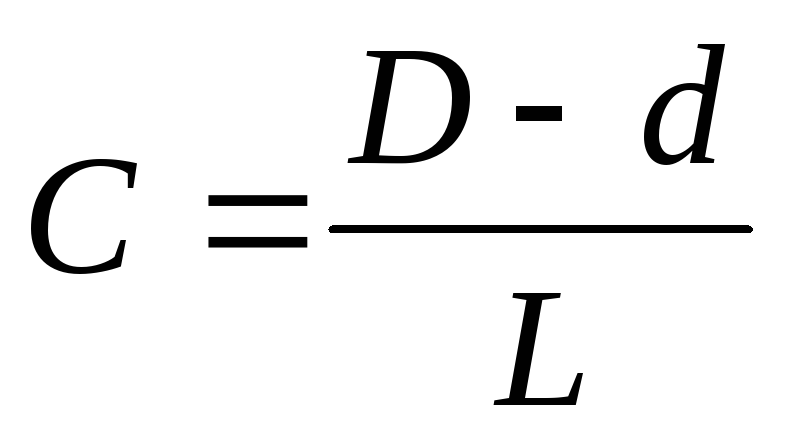 
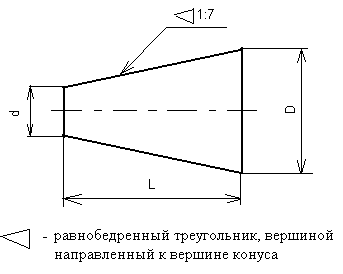
Рисунок 6.2
Вопросы для самоконтроля.
Что такое уклон?
Что такое конусность?
Сопряжение линий и лекальные кривые
Сопряжения применяются во многих деталях машин для плавного перехода линий.
Для построения сопряжений необходимо уметь строить касательную в данной точке окружности (рисунок 7.1 а) проводить из внешней точки прямую, касательную к окружности (рисунок 7.1 б). Помнить, что центры окружностей, соприкасающихся внешним образом, находятся на расстоянии суммы их радиусов (рисунок 7.1 в), а внутренним – на расстоянии их радиусов (рисунок 7.1 г), причем точка касания (сопряжения) всегда лежит на прямой, проходящей через их центры.
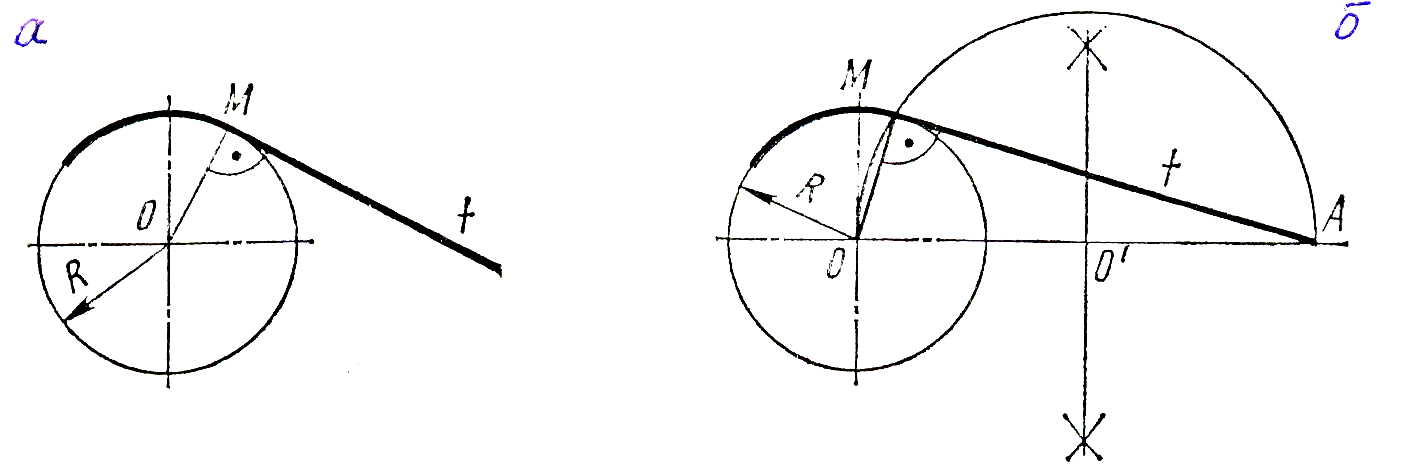
Рисунок 7.1
в г
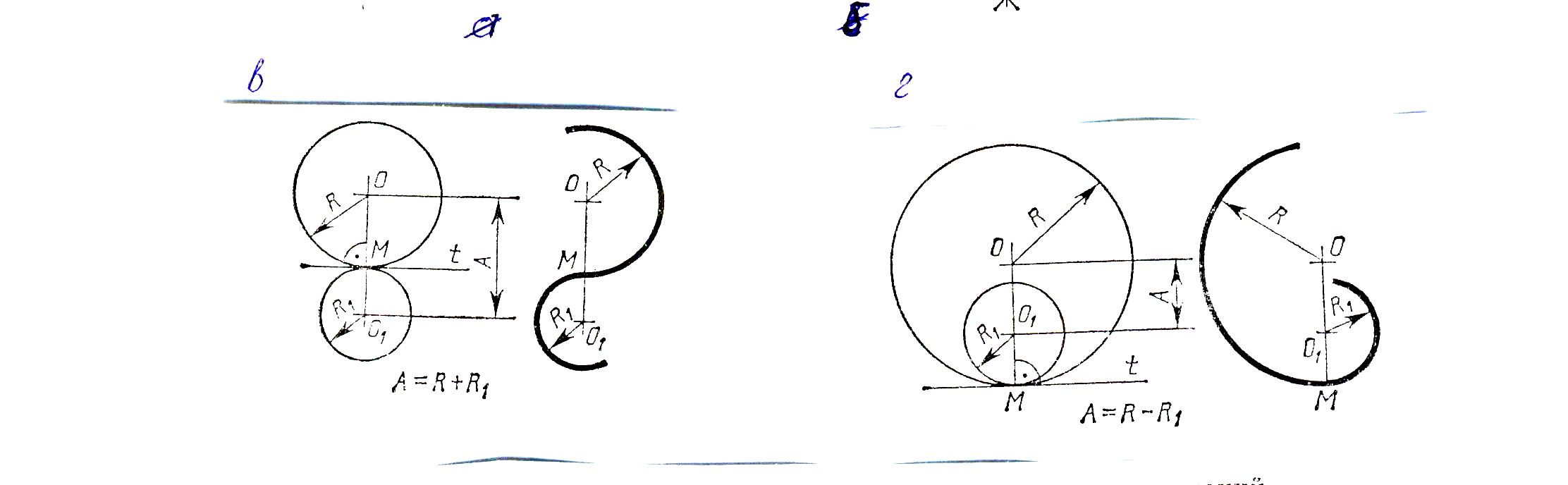
Рисунок 7.1
Изложенное позволяет легко уяснить последовательность решений задач на сопряжения, приведенных ни рисунке 7.2. ∂, е, ж, и, к.
∂ е ж
и к
Рисунок 7.2
Лекальные кривые обводят при помощи лекал. Наиболее часто применяют в технике следующее:
7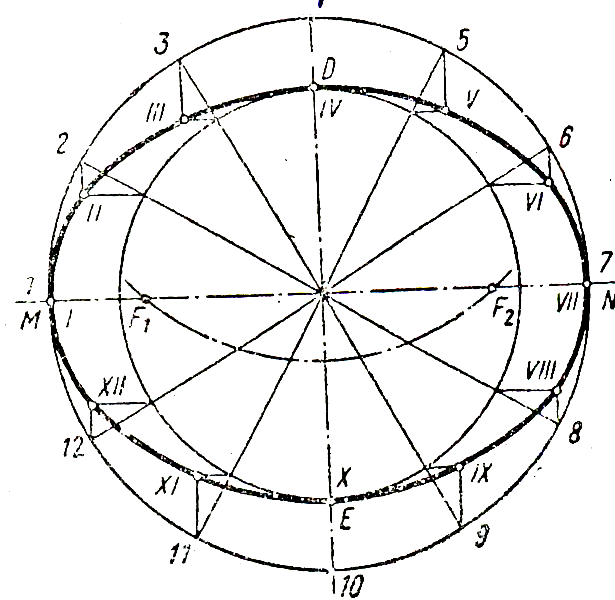
.1 Эллипс. Эллипсом
называется замкнутая кривая, для которой
сумма расстояний от любой точки до двух
точек – фокусов эллипса – есть величина
постоянная. Для построения эллипса
проводят две концентрические окружности,
диаметры которых равны осям эллипса
(рисунок 7.3). Эти окружности делят на
несколько равных частей (12-16). Через
точки деления на большей окружности
проводят вертикальные линии, через
соответствующие точки деления на малой
окружности – горизонтальные линии.
Пересечение этих линий даст точки
эллипса I, II, III
Рисунок 7.3
7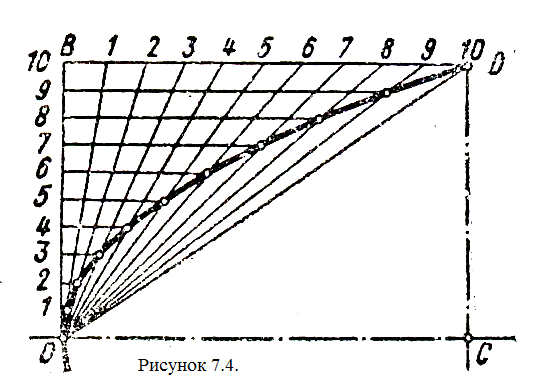
.2Парабола. Параболой
называется кривая, каждая точка которой
расположена на одинаковом расстоянии
от заданной прямой, носящей название
директрисы, и точки, называемой фокусом
параболы.
Даны вершина параболы О, одна из точек параболы D и направление оси ОС (рисунок 7.4). На отрезках ОС и СD строят прямоугольник, стороны этого прямоугольника ОВ и ВD делят на произвольное одинаковое число равных частей и нумеруют точки деления согласно рис. Вершину О соединяют с точками деления стороны ВD, а из точек деления отрезка ОВ проводят прямые, параллельные оси. Пересечение прямых, проходящих через точки с одинаковыми номерами, определяет ряд точек параболы (другие способы построения параболы см. в рекомендуемой литературе).
7.3 Циклоида. Траектория точки А, принадлежащей окружности, перекатываемой без скольжения по прямой, называется циклоидой (рисунок 7.5). Для ее построения от исходного положения точки А на направляющей прямой отк5ладывают отрезок АА1, равный длине данной окружности – 2πR. Окружность и отрезок АА1 делят на одинаковое число равных частей.
Восставляя перпендикуляры из точек деления прямой АА1 до пересечения с прямой, проходящей через центр данной окружности параллельно АА1, намечают ряд последовательных положений центра перекатываемой окружности О1, О2, О3,…, О8. Описывая из этих центров окружности радиуса R, отмечают точки пересечения с ними прямых, проходящих параллельно АА1 через точки деления окружности 1, 2, 3, 4 и т.д.
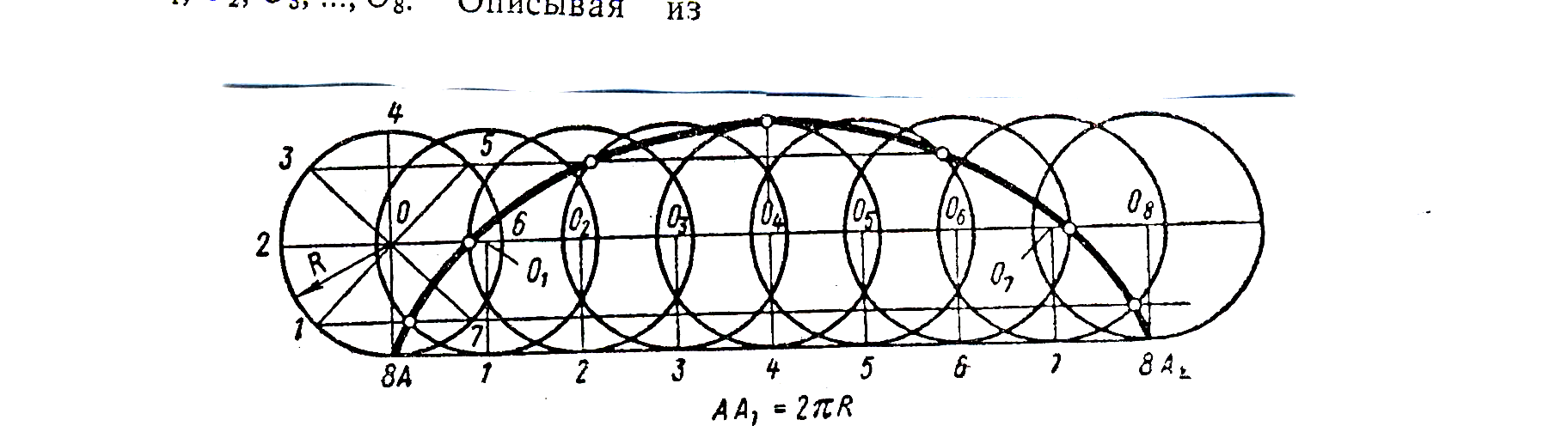
Рисунок 7.5
В пересечении горизонтальной прямой, проходящей через точку 1, с окружностью, описанной из центра О1, находится одна из точек циклоиды; в пересечении прямой, проходящей через точку 2, с окружностью, проведенной из центра О2, находится другая точка циклоиды и т.д. Соединяя полученные точки плавной кривой, получаем циклоиду.
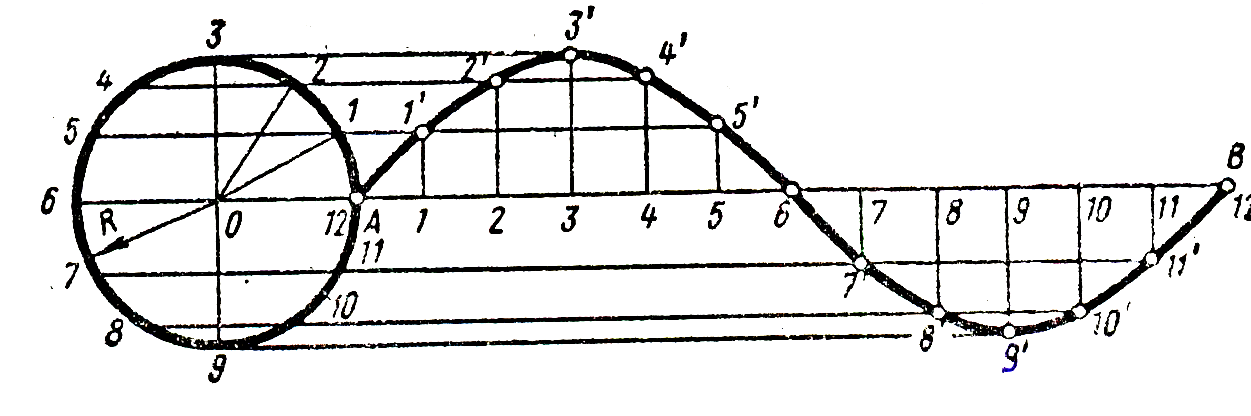
Синусоида. Для построения синусоиды делят окружность заданного радиуса на равные части (6, 8, 12, и т.д.) и на продолжении осевой линии от условного начала – точки А – проводят отрезок прямой АВ, равный 2πR. Затем прямую делят на такое же число равных частей, как и окружность (6, 8, 12 и т. Д.). Из точек окружности 1,2, 3, …, 12 проводят прямые линии параллельно выбранной прямой до пересечения с соответствующими перпендикулярами, восстановленными или опущенными из точек деления прямой.Полученные точки пересечения (1/, 2/ , 3/, …, 12/) и будут точками синусоиды с периодом колебания, равным 2πR.
π
Рисунок 7.6
7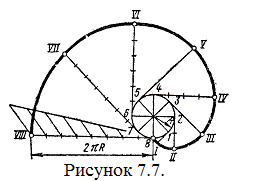
.5
Эвольвента (развертка
круга). Эвольвентой называется траектория,
описываемая каждой точкой прямой линии,
перекатываемой по окружности без
скольжения.
В машиностроении по эвольвенте очерчивают профиль головок зубьев зубчатых колес.
Для
построения эвольвенты окружность
предварительно делят на произвольное
число n равных частей; в точках деления
проводят касательные к окружности,
направленные в одну сторону. На
касательной, проведенной через последнюю
точку деления, откладывают отрезок,
равный длине окружности 2πR,
и делят его на то же число n равных частей.
Откладывая на первой касательной одно
деление, равное 
,
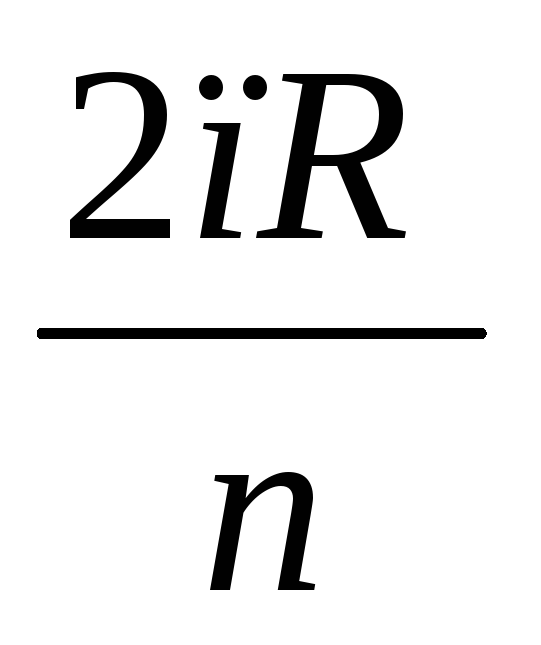на второй – два, на третьей – три и т.д.,
получают ряд точек I, II, III,IV
и т.д., которые соединяют по лекалу
Вопросы для самоконтроля.
На каких двух положениях геометрии основано построение сопряжений?
Перечислите элементы сопряжений.
Как построить эллипс?
Пандусы для маломобильных групп населения наклонные -Полезная информация
Уклон пандуса — одна из важнейших его характеристик — если наклонные поверхности пандуса выполнены с уклоном, превышающим нормы — его использование небезопасно как для инвалидов, так и для родителей с детскими колясками. Величина допустимого уклона пандуса регламентируется СП 59.13330.2012 «Доступность зданий и сооружений для маломобильных групп населения» — актуализированная версия СНиП 35-01-2001, документ введен в действие 01.01.2013.
Нормативный угол наклона пандуса для колясок должен быть не более 1:20 (5% или 2,86 градусов) и длина одного марша пандуса не более 8 м. В ряде случаев допускается увеличение максимального уклона пандуса:
- до 1:12 (8% или 4,76 градуса) — для временных сооружений и объектов инфраструктуры, при условии, что перепад высот между горизонтальными площадками менее 0,5 м и длина одного марша пандуса не более 6,0 м;
- до 1:10 (10% или 5,71 градуса) — при перепаде высот полов менее 0,2 м.
Как рассчитать угол наклона пандуса?
Вычисляется уклон пандуса с помощью формулы: наклон пандуса = H / L, где: H — перепад высот, который необходимо оборудовать пандусом, а L — длина горизонтальной проекции наклонного участка пандуса (нажмите для увеличения).
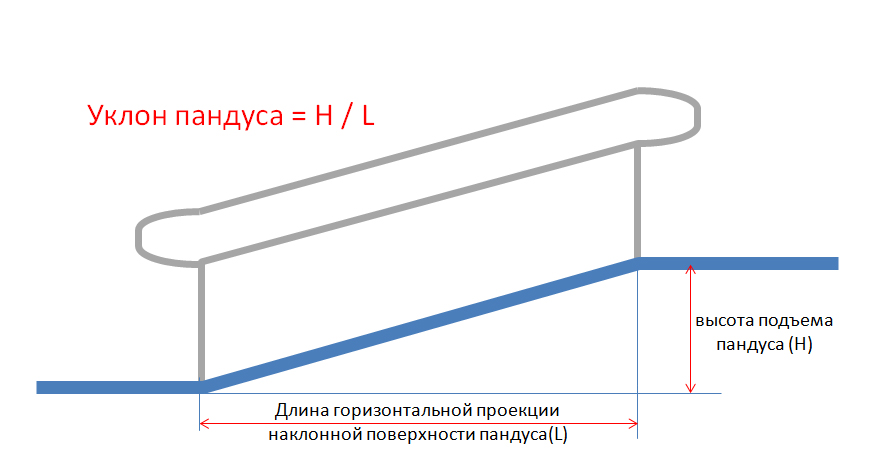
Например, нам необходимо рассчитать пандус для входа в здание, высота крыльца составляет 0,4 м. В данном случае необходимо использовать соотношение 1:12, составляя простую пропорцию получаем L=12*0.4 м = 4,8 м. Вычисляем длину наклонной поверхности пандуса = корень квадратный из (4,82+ 0,42) = 4,8 м Пандус может быть устроен без горизонтальных площадок, так как длина его наклонных поверхностей менее 6 м.
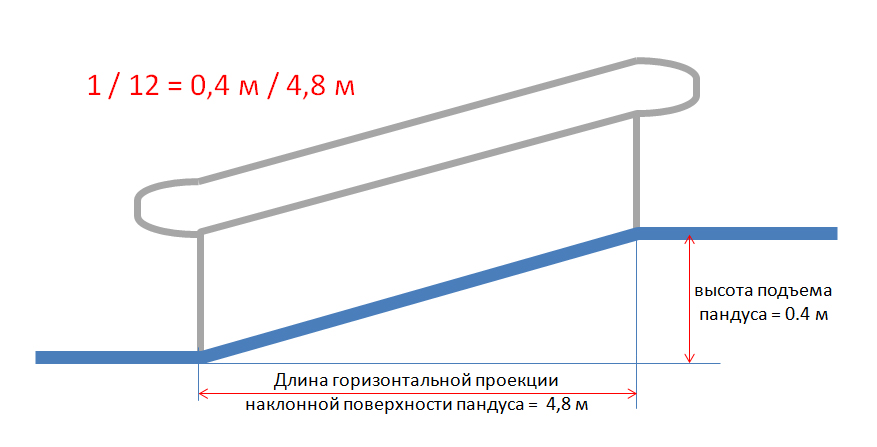
Если говорить о единицах измерения, то наклон пандуса может быть выражен в градусах, процентах и в виде отношения высоты к длине:
| Норматив | Соотношение | Значение в % | Значение в градусах |
|---|---|---|---|
| стандартный по СП 59.13330.2012 | 1:20 | 5% | 2,86 градуса |
| для временных сооружений | 1:12 | 8% | 4,76 градуса |
| при перепаде высот до 0,2 м | 1:10 | 10% | 5,71 градуса |
Уклон пандуса по СНиП 35-01-2001 и СП 59.13330.2012
В обозначенных выше документах есть разночтения по стандартной величине уклона пандусов, так в СНиП 35-01-2001 допустимый уклон пандуса составляет 1:12 (или 8%), в то время как по СП 59.13330.2012 — он равен 1:20 (или 5%).
Учитывая, что СНиП 35-01-2001 является национальным стандартом, утвержденным Распоряжением Правительства РФ от 21 июня 2010 г. № 1047-р, а также, если заказчиком не выдвигается требование спроектировать пандус по СП 59.13330.2012, предлагаем своим клиентам проектирование и изготовление пандусов по нормативам, обозначенным в СНиП 35-01-2001, т.е.:
- допустимый уклон пандуса — 1:12 (или 8%, или 4,76 градуса).
| Пандус для маломобильных групп |
Уклоны. Практика — на уровне глаз — ЖЖ
Часть первая — теоретическая, в которой разбираем, что такое уклонЧасть вторая — техническая, про моделирование уклонов в 3D программах (ArchiCAD и SketchUp)
Часть третья — практическая, примеры из жизни
Время от времени приходится иметь дело с уклонами вообще, и пандусов в частности. «Один к шести», «один к двенадцати», десять процентов, восемь процентов и т.п. Что это? Теоретически это мы разобрали ранее, но хотелось бы знать, как это выглядит в натуре, чтобы понимать как будет «работать» то, что начертишь. В чём разница для «пользователя»? О чём говорят цифры: полого это или круто, удобно или неудобно, и насколько одно отличается от другого?
Пандусы
В СНиПе 31-06-2009 «Общественные здания и сооружения» (п. 5.6) по поводу уклонов пандусов говорится:
Уклон пандусов на путях передвижения людей не должен превышать:
внутри здания, сооружения — 1:6; снаружи — 1:8; на путях передвижения инвалидов на креслах-колясках, в том числе в стационарах лечебных учреждений — от 1:10 до 1:12.
На фото ниже представлены пандусы внутри здания с указанными уклонами — 1:6 и 1:12. Сразу видно, что 1/6 круче, чем 1/12. Заметно круче.
Посмотрели, теперь опишем физические ощущения от ходьбы по данным пандусам, и начнём с малого уклона.
1/12
Он же 8% (i=0,08), он же 4,8°. Это максимально допустимый уклон пандуса для инвалидов, согласно
СНиП 35-01-2001 «Доступность зданий и сооружений для маломобильных групп населения», раздел «Лестницы и пандусы»
п.3.29 Максимальная высота одного подъема (марша) пандуса не должна превышать 0,8 м при уклоне не более 8 %.
Стоит отметить, что там же, в разделе «Участки и территории» указана меньшая цифра:
3.3 Продольный уклон пути движения, по которому возможен проезд инвалидов на креслах-колясках, как правило, не должен превышать 5 %
То есть уклон вне зданий должен быть более пологим. Почему так? Условиями из пункта 3.29 вводятся ограничения в виде перепада высот (0,8 метра) и максимального уклона (8%). При данных условиях максимальная длинна горизонтальной проекции пандуса составит 9,6 метра. В п.3.3 таких ограничений нет, а значит длина может быть любой. Важно, что на удобство перемещения по наклонной плоскости влияет не только величина уклона, но и длинна наклонной поверхности. Поэтому, чем больше длина пандуса, тем меньше должен быть уклон. Даже крутой уклон, преодолеваемый за один шаг, может восприниматься легче, чем более пологий, но продолжительный. Дальнейшие примеры наглядно продемонстрируют, что такое 8% без ограничения длины. Мало не покажется.
Подъём
Переход от ровной поверхности к наклонной почти не заметен, но примерно на шестом шаге инерция горизонтального движения заканчивается, и начинает ощущаться лёгкий подъём.
Спуск
С первого шага отчётливо ощущается изменение характера поверхности (наклон плоскости). При каждом шаге чувствуется небольшой провал.
По ощущениям идти по нему не сложно, но шаг уже явно не такой как по ровной поверхности. Уже вполне отчётливо чувствуется уклон. Если он чувствуется для обычного пешехода, то думаю, что для человека на инвалидной коляске он ощутим очень даже. Подтверждением этого могут быть слова автора книги «Доступная среда глазами инвалида» Елены Геннадьевны Леонтьевой eleont:
Уклон поверхности до 5%, на мой взгляд, можно называть не пандусом, а просто изменением рельефа, выравниванием поверхности, пологим съездом, так как при таком уклоне инвалиду на коляске не требуется посторонняя помощь.
Уклон более 5% вызывает определенные трудности для инвалида на коляске, поэтому необходима установка поручней с двух сторон или помощь сопровождающего.
Архитекторы и проектировщики, имейте это в виду. Если есть возможность заложить в проект более пологий пандус – делайте обязательно. 1/16 (6%) – хорошо, 1/18 – замечательно, 1/20 (5%) – просто великолепно! Прислушайтесь к мнению людей в инвалидной коляске, и не дай нам Бог оказаться на их месте.
Интересно, что при уклоне 1/12 (8%) перепад высоты на один шаг (60 см) составляет 5 см. В нормах тоже фигурируют 5 см.[Нажмите, чтобы прочитать]
СНиП 31-06-2009 «Общественные здания и сооружения», п.5.9. В полу на путях движения не допускаются перепады высотой менее трех ступеней (при высоте ступеней не менее 0,12 м) и пороги выше 0,05 м.
или
СНиП 2.07.01-89* «Градостроительство. Планировка и застройка городских и сельских поселений», п.6.24. В селитебных районах, в местах размещения домов для престарелых и инвалидов, учреждений здравоохранения и других учреждений массового посещения населением следует предусматривать пешеходные пути с возможностью проезда механических инвалидных колясок. При этом высота вертикальных препятствий (бортовые камни, поребрики) на пути следования не должна превышать 5 см; не допускаются крутые (более 100‰) короткие рампы, а также продольные уклоны тротуаров и пешеходных дорог более 50‰. На путях с уклонами 30 — 60‰ необходимо не реже чем через 100 м устраивать горизонтальные участки длиной не менее 5 м.
По моим наблюдениям перепады высотой до 4 см при движении практически не замечаются. А вот 5 см это та крайняя высота, которая уже слабо, но ощущается как препятствие. Его еще явно не переступаешь, но уже нога движется иначе. Колено приподнимается чуть выше, чем при ходьбе по ровной поверхности, и стопа как бы переносится над препятствием.
Почему это так, в какой-то мере можно объяснить тем, что «центр тяжести тела во время Х. совершает движения во всех трёх плоскостях. По вертикали амплитуда его перемещений достигает 4—5 см»— М.: Советская энциклопедия 1969—1978
В связи с этим любопытным представляется, что СНиП 35-01-2001 «Доступность зданий и сооружений для маломобильных групп населения» требует в местах пересечения тротуаров с проезжей частью высоту не более 4 см.
3.4 Высота бортового камня в местах пересечения тротуаров с проезжей частью, а также перепад высот бордюров, бортовых камней вдоль эксплуатируемых газонов и озелененных площадок, примыкающих к путям пешеходного движения, не должны превышать 0,04 м.
Скорее всего, что в данном случае такая цифра вытекает из возможности колеса коляски преодолевать такие перепады высот, а не из-за особенностей ходьбы пешеходов. Хотя Елена Геннадьевна, в своей книге, даёт такой комментарий по этому поводу:
В России почему-то считается, что все инвалиды без исключения могут без проблем преодолеть перепад в 4 см. На самом деле это не так. В международной практике максимально допустимая высота перепада уровней составляет не более 1,3–1,5 см.
Леонтьева Е.Г. Доступная среда глазами инвалида: научно-популярное издание. – Екатеринбург: «БАСКО», 2001. – с.37.
Тем не менее такая норма на руку и пешеходам, так как обеспечивает для них постоянство ритма ходьбы, а значит и её удобство и комфорт.
1/6
Он же 17% (i=0,17), он же 9,5°. Это предельный, максимально допустимый, уклон пандуса для передвижения людей внутри здания, согласно
СНиП 31-06-2009 «Общественные здания и сооружения» п.5.6, который уже воспринимается «горкой». Круче делать нельзя.
Подъём
С первого шага ритм и характер ходьбы меняется — скорее поднимаешься, чем идёшь вперёд. Скорость заметно падает. Шаг короче обычного, тело наклоняется вперёд, чувствуются усилия толчковой ноги. Для придания телу дополнительной динамики в работу включаются руки. Идти по нему не легко, есть ощущение, что по лестнице перемещаться легче. Может быть просто это связано с непривычностью движений, а не с количеством прилагаемых усилий.
Спуск
Чувствуется «тянущая» вперёд сила, для противодействия которой корпус тела отклоняется назад. При каждом шаге но́ги пружинят, и прилагаются усилия для гашения силы ускорения. Иначе шаг легко может перейти в бег.
Дороги
Выше был показан уклон 8% (1/12). Но это было внутри здания, а теперь рассмотрим его снаружи.
Подходящие параметры есть у дороги и тротуаров по пр.Ватутина (от ул.Костюкова до ул.5 Августа), где на перекрёстке пр.Ватутина-ул.Костюкова, в направлении центра города, установлен знак 1.13 «Крутой спуск» с указаным уклоном 9%.
Думаю, что те, кто тут проходил или проезжал уклон этот маленьким не назовут
Как известно, знак указывает лишь угол между началом и концом участка дороги, а в этом промежутке, в каждый отдельный момент, угол может быть разным. Что и показали натурные замеры. Уклон 9% соответствует лишь участку дороги от перекрёстка пр.Ватутина-ул.5 Августа до пешеходного моста. Дальше, до пересечения с ул.Костюкова, уклон равен 8%.
Длина участка с уклоном 8-9% около 250 метров. Не всякий велосипедист осиливает такой подъём, многие идут пешком.
8% Спуск и подъём
Спуск не вызывает особых трудностей, а ощущения при ходьбе были описаны выше. Длительный же подъём, при таком уклоне, даётся не легко. Во время подъёма чувствуется как переставляются ноги, примерно так же, как по лестнице. Обращаешь на это внимание. Мышцы спины начинают выделять тепло. К концу подъёма наблюдается учащённое сердцебиение, увеличивается глубина дыхания и ощущается напряжение мышц ног, в особенности икр.
Если продолжить идти по пр.Ватутина в сторону центра, то на пути встретятся участки с уклонами 5, 7 и 4%
7%
Близко по ощущениям к 8%, но немного легче. Ещё нет глубокого дыхания, учащённого сердцебиения и взмокшей спины. Лёгкий вариант 8%.
5%
Спуск лёгкий, но перемещение уже не совсем «свободное», как при ходьбе по ровной поверхности.
При подъёме чувствуется слабое, еле заметное, приложение усилий, преодоление. Дыхание держится в «нормальном» режиме.
Выводы
Уклон поверхности до 4% включительно не имеет каких-либо существенных различий с ходьбой по горизонтальной поверхности. 5% представляется граничным значением, при котором уже начинают появляться лёгкие изменения в характере ходьбы. Ещё двигаешься без затруднений, но уже различается наклон поверхности. Уклоны больше 5% меняют режим ходьбы, и чем больше уклон, тем изменения заметнее. От величины уклона поверхности зависит расстояние, которое можно пройти без утомления. Чем больше уклон, тем меньше расстояние. Например, при уклоне 2% пройти 1-2 километра не составит труда, а если уклон 8%, то можно запыхаться уже на 150 метрах (при подъёме).
Для объяснения этого можно вспомнить то, что удалось найти по механике ходьбы. Для демонстрации движения человека по наклонной плоскости, я использовал картинку из статьи Адама Саммерса (Adam Summers) «The Biomechanist Went Over the Mountain», размещённой на сайте Natural History Magazine. Повторю её тут.
Данные и картинка © Natural History Magazine
На ней показана последовательность движений человека при ходьбе по ровной поверхности (1), с уклоном 5°(~8%) (2) и уклоном 15°(~26%) (3). Белыми точками обозначено положение общего центра масс (ОЦМ) тела человека, который при ходьбе действует как груз на конце перевёрнутого маятника. Амплитуда перемещений ОЦМ по вертикали составляет 4-5 см, при этом бо́льшая часть энергии (около 65%), затраченной на изменение высоты ОЦМ, сохраняется. Ходьба по плоскости с небольшим уклоном увеличивает затраты энергии на работу маятника, и амплитуду перемещений ОЦМ (2). Часть энергии расходуется на тепло, выделяемое мышцами, а часть всё ещё остаётся для последующих шагов. Но когда уклон становится больше (3), то уже вся энергия тратится на один шаг (так же, как и при восхождении по лестнице).
Отсюда можно вывести ориентировочную классификацию уклонов для пешеходной ходьбы на большие расстояния:
• идеальный 0-2%
• нормальный 2-4%
• допустимый 5-6%
• предельный 7-8%
всё что сверх 8% можно считать затруднительным с различной степенью тяжести.
Таким образом, судя по мои субъективные впечатлениям, увеличение затрат энергии на работу маятника начинается с уклона 5%.
Разница между уклонами в 2% ощущается и различается кинестетически (т.е. суставами и мускулами в движении).
При больших отрезках одного уклона изменения даже в 1% могут быть визуально заметны.
[Инструмент]
Инструмент
Для измерения уклонов использовал самостоятельно изготовленный прибор простой конструкции. Деревянная рейка длиной 1,10 метра (уж какая была), к которой прикреплён плотный картон (3 мм). На нём лист со шкалой и стрелка с грузиком. Можно в качестве стрелки использовать грузик подвешеный на нитке, но в таком случае придётся дольше ждать прекращеня колебаний.
шкала уклономера в процентах pdf, svg
Есть и второй, более современный и компактный, вариант — с помощью приложения Smart Protractor.
У него в настройках можно выставить показ измерений в радианах, градусах или процентах.
Неплохое приложение, но при измерении малых уклонов, из-за небольшой длины смартфона, точность может быть ±1%, а это многовато. В общем, использовать можно, но для качественного измерения нужно вначале точно откалибровать, а потом желательно сделать несколько замеров и сравнить их с показаниями механического уклономера. Это для понимания условий точного измерения (как держать смартфон, на что ставить, и т.п.)
На этом трилогия «Уклоны» завершена
до этого были:
Часть первая — теоретическая, в которой разбираем, что такое уклон
Часть вторая — техническая, про моделирование уклонов в 3D программах (ArchiCAD и SketchUp)
Напоследок скажу, что всё что описано выше не более чем личные впечатления. Мне это нужно, чтобы в процессе проектирования не только опираться на цифры из нормативных документов, но и иметь кинестетическое представление о них. Также буду признателен, если поделитесь своими впечатлениями, наблюдениями или дополнениями.
© Gre-kow, 2015. gre-kow.livejournal.com
При копировании активная ссылка http://gre-kow.livejournal.com/26916.html обязательна