Угол в 90 градусов: Прямой угол — Википедия – Как сделать прямой угол между стенами

Содержание

Прямоугольный треугольник — Википедия

Прямоугольный треугольник

Прямоуго́льный треуго́льник — это треугольник, в котором один угол прямой (то есть 90 градусов).

Соотношения между сторонами и углами прямоугольного треугольника лежат в основе тригонометрии.

Сторона, противоположная прямому углу, называется гипотенузой (сторона c на рисунке выше).
Стороны, прилегающие к прямому углу, называются катетами. Сторона a может быть идентифицирована как прилежащая к углу В и противолежащая углу A, а сторона b — как прилежащая к углу A и противолежащая углу В.

Если длины всех трёх сторон прямоугольного треугольника являются натуральными числами, то треугольник называется пифагоровым треугольником, а длины его сторон образуют так называемую пифагорову тройку.

Признаки равенства прямоугольных треугольников[править | править код]

По двум катетам: если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны.
Этот признак немедленно следует из первого признака равенства треугольников, так как у двух треугольников будут равны по два катета и прямой угол.

По катету и прилежащему острому углу: если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны
Этот признак немедленно следует из второго признака равенства треугольников, так как у двух треугольников будут равен один катет, прилежащий к нему угол и прямой угол.

По гипотенузе и острому углу: если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
Этот признак следует из второго признака равенства треугольников, так как вторые острые углы будут равны по теореме о сумме углов треугольника и у треугольников будут равны гипотенузы и два прилежащих к ней угла.

По гипотенузе и катету: если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.

Этот признак докажем так. Наложим два треугольника друг на друга так, чтобы получить равнобедренный треугольник, то есть совместим их равными катетами так, чтобы углы, лежащие при этих катетах, лежали в разных плоскостях. Так как гипотенузы равны, получившийся треугольник — равнобедренный, тогда углы при основании равны. Тогда два прямоугольных треугольника будут равны по гипотенузе и острому углу.

По катету и противолежащему острому углу: если катет и противолежащий острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.

Этот признак доказывается так: если один из острых углов первого треугольника равен острому углу второго треугольника, то второй острый угол будет известен по теореме о сумме углов треугольника. Так как второй острый угол прилегает к катету, то далее равенство треугольников будет доказываться по предыдущей теореме.

Далее предполагаем, что a{\displaystyle a} и b{\displaystyle b} длины катетов, а c{\displaystyle c} длина гипотенузы

Площадь прямоугольного треугольника равна половине произведения двух его катетов. То есть,
S=12ab.{\displaystyle S={\tfrac {1}{2}}ab.}

Для медиан ma{\displaystyle m_{a}}, mb{\displaystyle m_{b}} и mc{\displaystyle m_{c}} выполняется следующее соотношение:

ma2+mb2=5mc2=54c2.{\displaystyle m_{a}^{2}+m_{b}^{2}=5m_{c}^{2}={\frac {5}{4}}c^{2}.}
- В частности, медиана, падающая на гипотенузу, равна половине гипотенузы.

Высота[править | править код]

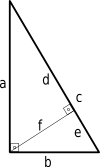$m_{a}^{2}+m_{b}^{2}=5m_{c}^{2}={\frac {5}{4}}c^{2}.$ Высота прямоугольного треугольника.

Если высота проведена к гипотенузе, то треугольник делится на два меньших треугольника, подобных исходному и подобных друг другу. Из этого следует, что в обозначениях, показанных на диаграмме:^[1]

f2=de,{\displaystyle \displaystyle f^{2}=de,} (иногда это называют теоремой высоты прямоугольного треугольника)

b2=ce,{\displaystyle \displaystyle b^{2}=ce,}

a2=cd{\displaystyle \displaystyle a^{2}=cd}

В прямоугольном треугольнике высота, опущенная из вершины прямого угла на гипотенузу, делит гипотенузу в таком отношении, в каком находятся квадраты прилежащих катетов, то есть

d:e=a2:b2,{\displaystyle \displaystyle d:e=a^{2}:b^{2},}

Кроме того высота, опущенная на гипотенузу, связана с катетами прямоугольного треугольника соотношением:^[2]^[3]

1a2+1b2=1f2.{\displaystyle {\frac {1}{a^{2}}}+{\frac {1}{b^{2}}}={\frac {1}{f^{2}}}.}

f=abc.{\displaystyle f={\frac {ab}{c}}.}

Также если прямоугольный треугольник является равнобедренным, то высота, опущенная на гипотенузу будет равна:

f=rδS =r(1+2){\displaystyle f=r\delta _{S}\ =r(1+{\sqrt {2}})}, где r{\displaystyle r} — это радиус вписанной окружности, а δS{\displaystyle \delta _{S}} — серебряное сечение.

Характеристики[править | править код]

Треугольник ABC со сторонами a, b, c (где c — самая длинная сторона), с описанной окружностью радиуса R является прямоугольным треугольником тогда и только тогда, когда верно любое из следующих соотношений:^[4]

Тригонометрические соотношения[править | править код]

Тригонометрические функции для острых углов можно определить как отношения сторон прямоугольного треугольника. Для любого данного угла можно построить прямоугольный треугольник, содержащий такой угол, и со сторонами: противолежащим катетом, прилежащим катетом и гипотенузой, связанными с этим углом определёнными выше соотношениями. Эти отношения сторон не зависят от конкретного выбранного прямоугольного треугольника, а зависят только от заданного угла, так как все треугольники, построенные таким образом, являются подобными. Если для заданного угла α, противолежащий катет, прилежащий катет и гипотенузу обозначить a, b и c соответственно, то тригонометрические функции имеют вид:

sin⁡α=ac,cos⁡α=bc,tg⁡α=ab,ctg⁡α=ba,sec⁡α=cb,csc⁡α=ca.{\displaystyle \sin \alpha ={\frac {a}{c}},\,\cos \alpha ={\frac {b}{c}},\,\operatorname {tg} \alpha ={\frac {a}{b}},\,\operatorname {ctg} \alpha ={\frac {b}{a}},\sec \alpha ={\frac {c}{b}},\,\,\csc \alpha ={\frac {c}{a}}.}

И таким образом:

Катет, противолежащий углу, равен произведению гипотенузы на синус этого угла

a=c⋅sin⁡α,b=c⋅sin⁡β.{\displaystyle a=c\cdot \sin \alpha ,\,b=c\cdot \sin \beta .}

Катет, прилежащий углу, равен произведению гипотенузы на косинус этого угла

a=c⋅cos⁡β,b=c⋅cos⁡α.{\displaystyle a=c\cdot \cos \beta ,\,b=c\cdot \cos \alpha .}

Катет, противолежащий углу, равен произведению второго катета на тангенс угла

a=b⋅tg⁡α,b=a⋅tg⁡β.{\displaystyle a=b\cdot \operatorname {tg} \alpha ,\,b=a\cdot \operatorname {tg} \beta .}

Катет, прилежащий углу, равен произведению второго катета на котангенс угла

a=b⋅ctg⁡β,b=a⋅ctg⁡α.{\displaystyle a=b\cdot \operatorname {ctg} \beta ,\,b=a\cdot \operatorname {ctg} \alpha .}

Гипотенуза равна отношению катета к синусу противолежащего угла, и/или частному отношению катета и косинуса прилежащего угла (угла между ними)

c=asin⁡α=bsin⁡β=acos⁡β=bcos⁡α.{\displaystyle c={\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }}={\frac {a}{\cos \beta }}={\frac {b}{\cos \alpha }}.}

Специальные прямоугольные треугольники[править | править код]

Значения тригонометрических функций можно точно оценить для определённых углов, используя прямоугольные треугольники с особыми значениями углов. К таким треугольникам относятся треугольник 30-60-90, который можно использовать для оценки тригонометрических функций для любых значений, кратных π/6, и треугольник 45-45-90 (равнобедренный прямоугольный), который можно использовать для оценки тригонометрических функций для значений, кратных π/4. В частности,

Катет, лежащий против острого угла в 30° (и соответственно, прилежащий к углу в 60°), равен половине гипотенузы.

Теорема Фалеса[править | править код]

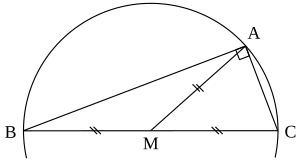$c={\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }}={\frac {a}{\cos \beta }}={\frac {b}{\cos \alpha }}.$

Медиана прямого угла треугольника

Теорема Фалеса утверждает, что если какая-нибудь точка A лежит на окружности диаметра BC (за исключением самих точек B и C), то △ABC представляет собой прямоугольный треугольник с прямым углом A. Обратное утверждение таково: если прямоугольный треугольник вписан в окружность, то гипотенуза будет её диаметром. Следствием является то, что длина гипотенузы равна удвоенному расстоянию от вершины прямого угла до середины гипотенузы. Верно также, что центр окружности, описывающей прямоугольный треугольник, является серединой гипотенузы, а её радиус равен половине длины гипотенузы.

Другие свойства[править | править код]

Радиус вписанной окружности в прямоугольный треугольник с катетами a и b и гипотенузой c равен:

r=a+b−c2=aba+b+c.{\displaystyle r={\frac {a+b-c}{2}}={\frac {ab}{a+b+c}}.}

Если отрезки длиной p и q, исходящие из вершины C, делят гипотенузу на три равных отрезка длины c/3, то:^[5]^{:pp. 216-217}

p2+q2=5(c3)2.{\displaystyle p^{2}+q^{2}=5\left({\frac {c}{3}}\right)^{2}.}

Прямоугольный треугольник является единственным треугольником с двумя, а не тремя, отличными друг от друга вписанными квадратами.^[6]

Пусть h и s (h>s) сторонами двух квадратов, вписанных в прямоугольный треугольник с гипотенузой c. Тогда:

1c2+1h3=1s2.{\displaystyle {\frac {1}{c^{2}}}+{\frac {1}{h^{2}}}={\frac {1}{s^{2}}}.}

Периметр прямоугольного треугольника равен сумме двух радиусов вписанной и четырех описанных окружностей:

P=2r+4R{\displaystyle P=2r+4R}

Если заданы S и r, то стороны треугольника находятся по формулам:

a=12(r+Sr−r2−6S+S2r2){\displaystyle a={\frac {1}{2}}\left(r+{\frac {S}{r}}-{\sqrt {r^{2}-6S+{\frac {S^{2}}{r^{2}}}}}\right)}

b=12(r+Sr+r2−6S+S2r2){\displaystyle b={\frac {1}{2}}\left(r+{\frac {S}{r}}+{\sqrt {r^{2}-6S+{\frac {S^{2}}{r^{2}}}}}\right)}

c=Sr−r{\displaystyle c={\frac {S}{r}}-r}

Во всех прямоугольных треугольниках медиана, опущенная на гипотенузу, равна половине гипотенузы.

↑ Wentworth p. 156
↑ Voles, Roger, «Integer solutions of a−2+b−2=d−2{\displaystyle a^{-2}+b^{-2}=d^{-2}},» Mathematical Gazette 83, July 1999, 269—271.
↑ Richinick, Jennifer, «The upside-down Pythagorean Theorem, » Mathematical Gazette 92, July 2008, 313—317.
↑ Andreescu, Titu and Andrica, Dorian, «Complex Numbers from A to…Z», Birkhäuser, 2006, pp. 109—110.
↑ Posamentier, Alfred S., and Salkind, Charles T. Challenging Problems in Geometry, Dover, 1996.
↑ Bailey, Herbert, and DeTemple, Duane, «Squares inscribed in angles and triangles», Mathematics Magazine 71(4), 1998, 278—284.

Дополнительные углы — Википедия

Материал из Википедии — свободной энциклопедии

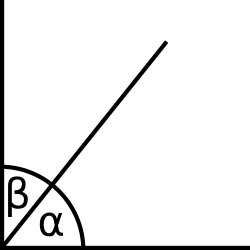Пара дополнительных углов, дополняющих друг друга до 90 градусов

Дополни́тельные углы́ — это пара углов, которые дополняют друг друга до 90 градусов.

Если два дополнительных угла являются соседними (то есть имеют общую вершину и разделяются только одной стороной), их не общие стороны образуют прямой угол.

В евклидовой геометрии два острых угла прямоугольного треугольника являются дополнительными, потому что сумма внутренних углов треугольника составляет 180 градусов, а прямой угол равен 90 градусам.

Синус одного из углов равен косинусу его дополнительного угла. Если углы A и B являются дополнительными, то верны равенства: sin2⁡A+sin2⁡B=1{\displaystyle \sin ^{2}A+\sin ^{2}B=1} и cos2⁡A+cos2⁡B=1.{\displaystyle \cos ^{2}A+\cos ^{2}B=1.}

Тангенс одного из углов равен котангенсу его дополнительного угла. Тангенсы дополнительных углов взаимно обратны.

Секанс одного из углов равен косекансу его дополнительного угла.

Префикс «ко-» в названиях некоторых тригонометрических функций происходит лат. complementum — дополнение.

Как сделать угол в ванной 90 градусов > %

Зачем и когда необходим прямой угол в ванной комнате?

Ванная комната предполагает установку ванны. Только в этом случае важно соблюдение прямого угла, где она будет примыкать. Это необходимо для предотвращения затекания воды. При незначительных отклонениях от 90 градусов, этот дефект исправим и не создает большой проблемы. Просто для заделки увеличенного промежутка потребуется больше силикона.

Установка ванны в угол 90 градусов

Как выход, в подобных ситуациях практикуется устройство штробы в стене, на уровне бортика ванны . Прямой угол в этом случае возникает уже внутри стены (штробы).

Построение прямого угла в любом помещении начинается на этапе возведения стен. Если в этот момент была допущена большая ошибка, то исправить ее штукатуркой уже нельзя. Потому, как толщина слоя в конце стены может достигать 10-15 см.

Как сделать прямой угол и возможно ли такое на этапе выравнивающей штукатурки?

Если отклонения от 90 градусов между стенами небольшое, то выполнение этого условия с помощью выравнивающей штукатурки вполне оправдано. Толщину выравнивающего слоя можно распределить между двумя стенками или взять одну стенку за базовую, выставить там маяки по минимуму. Обычно это длинная стенка. Тогда выравнивающий слой, создающий прямой угол, будет на второй , короткой стене. Это даст возможность избежать больших слоев.

Можно сделать сперва штукатурку на базовой стене, а потом заняться построением 90 градусов с помощью маяков на второй плоскости. А можно сразу заняться построением прямого угла с помощью маяков на обеих плоскостях . Как это получилось в нашем случае.

Между двумя отметками будущей штукатурки (саморезами в пластмассовых дюбелях 1 и 2 на фотографии) , с помощью клина, установить промежуточную, для уголка.
Первый этап по созданию прямого угла
С помощью уголка обозначить прямой угол. Проверить визуально насколько построение его возможно в конкретном случае на практике. Забить два дюбеля на второй стене (1 и 2 на фотографии).
Второй этап. Проверка угольником
С помощью клина или лески установить третий дюбель, который будет служить отметкой для штукатурного маяка в конце стены. Проверить последнюю отметку по отвесу – не упирается ли будущий маяк в стену.
Третий этап создания угла в 90 градусов
Еще раз все проверить на возможность уменьшения штукатурного слоя.

Соблюдение этого правила необходимо для всех углов в сан блоке или нет?

Это условие необходимо для угла, в котором предстоит установка ванны. Если ванна занимает все пространство между стенками – прямыми должны быть оба угла. В случае, если происходит неполное заполнение пространства между двумя стенками – достаточно 90 градусов в одном угле.

Но необходимо учитывать, что ванна может иметь отклонения от 90 градусов. Особенно чугунное литье. И тогда все танцы с бубном вокруг угла становятся напрасными. Проблема переходит на следующий этап – заделку стыка между ванной и стеной.

как узнать длинную сторону в треугольнике с углом 90 градусов? — itthink.ru

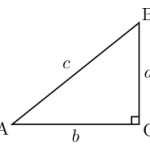
Прямоугольный треугольник — это треугольник, в котором один угол прямой (то есть составляет 90 градусов).
Соотношения между сторонами и углами прямоугольного треугольника лежат в основе тригонометрии.

Сторона, противоположная прямому углу, называется гипотенузой (сторона c на рисунке выше).
Стороны, прилегающие к прямому углу, называются катетами. Сторона a может быть идентифицирована как прилежащая к углу В и противолежащая углу A, а сторона b — как прилежащая к углу A и противолежащая углу В.

Если длины всех трёх сторон прямоугольного треугольника являются целыми числами, то треугольник называется пифагоровым треугольником, а длины его сторон образуют так называемую пифагорову тройку.

Признаки равенства прямоугольных треугольников
По двум катетам
Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны.
По катету и острому углу
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны.
По гипотенузе и острому углу
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
По гипотенузе и катету
Если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.

Далее предполагаем, что a и b длины катетов, а c длина гипотенузы (Теорема Пифагора)

c^2=a^2+b^2 (Квадрат стороны с равен сумме квадрата сторон a и b)

Площадь прямоугольного треугольника равна половине произведения двух его катетов. То есть,

S=\tfrac{1}{2}ab.

Для медиан m_a, m_b и m_c выполняется следующее соотношение:

m_a^2 + m_b^2 = 5m_c^2 = \frac{5}{4}c^2.

В частности, медиана, падающая на гипотенузу, равна половине гипотенузы.