Расчет лобовой балки в сборной лестнице по металлическим косоурам
Балку, на которую опирается лестничная площадка и косоуры называют лобовой. В этой статье мы рассмотрим особенности расчета такой балки.
Итак, у нас имеется кирпичная лестничная клетка. В уровне каждой площадки стены опираются металлические балки из швеллеров, а к этим балкам привариваются наклонные металлические косоуры. На балки опираются монолитные железобетонные лестничные площадки, на косоуры опираются сборные железобетонные ступени.
Рассчитаем лобовую балку, на которую опираются косоуры на отметке +3,000.
Собираем нагрузку на балку
Рассмотрим схему нагрузок на лобовую балку.
Во-первых, на нее приходится равномерно распределенная нагрузка от веса половины лестничной площадки, от временной нагрузки на этой площадке и нагрузка от собственного веса швеллера.
Во-вторых, на балку действует четыре сосредоточенные нагрузки от косоуров.
Определим нагрузку от собственного веса половины площадки (вторая половина приходится на другую балку). Ширина площадки 1350 мм, толщина 150 мм, объемный вес бетона 2,5 т/м³:
0,5∙1,35∙0,15∙2,5= 0,25 т/м – нормативная нагрузка;
1,1∙0,25 = 0,28 т/м – расчетная нагрузка.
Определим нагрузку от собственного веса швеллера, принимая его для начала №16 (вес 1 погонного метра швеллера равен 14,2 кг):
0,014 т/м – нормативная нагрузка;
1,05∙0,014 = 0,015 т/м – расчетная нагрузка.
Суммарная постоянная равномерно распределенная нагрузка на балку равна:
0,25 + 0,014 = 0,26 т/м – нормативная постоянная нагрузка;
0,28 + 0,015 = 0,3 т/м – расчетная постоянная нагрузка.
Определим временную равномерно распределенную нагрузку на балку. Площадь сбора нагрузки у нас с половины площадки, величина временной нагрузки 300 кг/м². В итоге:
0,5∙1,35∙0,3 = 0,2 т/м – нормативная временная нагрузка;
0,2∙1,2 = 0,24 т/м – расчетная временная нагрузка.
Полная равномерно распределенная нагрузка на балку равна:
qн = 0,26 + 0,2 = 0,46 т/м – нормативная полная нагрузка;
qр = 0,3 + 0,24 = 0,54 т/м – расчетная полная нагрузка.
Определим сосредоточенную нагрузку на балку от каждого косоура. Для этого нам нужно выяснить, какие нагрузки приходятся на косоур:
1) собственный вес половины косоура. Допустим, у нас косоур из швеллера №16, длина косоура 3,7 м, тогда вес половины косоура будет равен:
0,5∙0,0142∙3,7 = 0,026 т – нормативная нагрузка;
0,026∙1,05 = 0,028 т – расчетная нагрузка.
2) Вес ступеней. Так как каждая ступень опирается на два косоура, то нам нужно брать половину от веса каждой ступени. Косоур у нас опирается на две балки – вверху и внизу, т.е. на нашу балку приходится нагрузка с половины косоура, т.е. и от половины ступеней. Всего на косоур опирается 12 ступеней, и мы возьмем вес половины, т.е. 6 ступеней (5 основных массой 111 кг и 1 доборная массой 87 кг). Таким образом, сосредоточенная нагрузка на площадку от ступеней равна:
0,5∙(5∙0,111 + 1∙0,087) = 0,321 т – нормативная нагрузка;
1,1∙0,321 = 0,353 т – расчетная нагрузка.
3) Временная нагрузка от веса людей (300 кг/м²). Площадь сбора этой нагрузки определяется по тому же принципу, как и сбор нагрузок от собственного веса ступеней: берется половина площади шести ступеней. Нам известно, что площадь одной ступени равна 1,05х0,3 = 0,32 м², тогда временная сосредоточенная нагрузка от косоура равна:
0,5∙0,32∙6∙0,3 = 0,29 т – нормативная;
0,29∙1,2 = 0,35 т – расчетная.
Полная сосредоточенная нагрузка на лобовую балку от одного косоура равна:
Рн = 0,026 + 0,321 + 0,29 = 0,64 т – нормативная;
Рр = 0,028 + 0,353 + 0,35 = 0,73 т – расчетная.
Определим расчетный пролет балки.
Пролет балки в свету между стенами равен 2,2 м. Глубина опирания балки на стену равна 0,25 м с каждой стороны. Чтобы получить размер расчетного пролета, нужно к пролету в свету добавить по 1/3 глубины опирания балки с каждой стороны:
L₀ = 2.2 + 2∙0,25/3 = 2,4 м.
Вычислим максимальный нормативный изгибающий момент, действующий на балку
Расчетная схема балки показана на рисунке ниже. На балке выделено 6 точек, которые разбивают ее на 5 участков.
Для начала заменим распределенную нагрузку на каждом участке на сосредоточенную воспользовавшись формулой: N = qн∙L . Результаты сведем в таблицу.
В итоге, у нас получится следующая расчетная схема:
R1 и R6 – опорные реакции балки.
Найдем сумму моментов относительно точки 1, умножая каждую из сил на расстояние до опоры:
Зная, что момент на шарнирной опоре равен нулю, составим уравнение и найдем реакцию R6:
ΣМ1 = -4.397 + 2,4R6 = 0, отсюда R6 = 4.397/2,4 = 1,832 т.
Так как расчетная схема симметрична, сумма моментов относительно точки 6 и реакция R1 будут равны:
ΣМ6 = -4.397 + 2,4R1 = 0, отсюда R1 = 4.397/2,4 = 1,832 т.
Выполним проверку, зная, что сумма всех вертикальных сил должна быть равна нулю:
Проверка выполняется, реакции R6 и R1 определены верно.
Определим моменты в точках 1-6, зная, что на шарнирных опорах момент равен нулю, а в пролете момент равен сумме сил, расположенных по одну сторону от точки, каждая из которых умножена на расстояние от точки приложения силы до точки, в которой определяется момент.
М1 = 0.
М2 = 0,15∙R1+ 0,075∙N1-2 = 0,15∙1,832 + 0,075∙(-0,07) = 0,27 т∙м.
М3 = 1,1∙R1+ 1,025∙N1-2 + 0,95∙Р2 + 0,475∙ N2-3 = 1,1∙1,832 + 1,025∙(-0,07) + 0,95∙(-0,64) + 0,475∙(-0,44) = 1,13 т∙м.
М4 = 1,3∙R1+ 1,225∙N1-2 + 1,15∙Р2 + 0,675∙ N2-3 + 0,2∙Р3 + 0,1∙ N3-4 = 1,3∙1,832 + 1,225∙(-0,07) + 1,15∙(-0,64) + 0,675∙(-0,44) + 0,2∙(-0,64) + 0,1∙(-0,09) = 1,13 т∙м.
М5 = 2,25∙R1+ 2,175∙N1-2 + 2,1∙Р2 + 1,625∙ N2-3 + 1,15∙Р3 + 1,05∙ N3-4 + 0,95∙Р4 + 0,475∙ N4-5 = 2,25∙1,832 + 2,175∙(-0,07) + 2,1∙(-0,64) + 1,625∙(-0,44) + 1,15∙(-0,64) + 1,05∙(-0,09) + 0,95∙(-0,64) + 0,475∙(-0,44) = 0,27 т∙м.
М6 = 0.
Определим момент М0 в точке 0 в середине пролета. Для этого распределенную нагрузку на участке 3-0 заменим сосредоточенной по формуле N = qн∙L = 0,57∙0,1 = 0,06 т.
М0 = 1,2∙R1+ 1,125∙N1-2 + 1,05∙Р2 + 0,575∙ N2-3 + 0,1∙Р3 + 0,05∙ N3-4 = 1,2∙1,832 + 1,125∙(-0,07) + 1,05∙(-0,64) + 0,575∙(-0,44) + 0,1∙(-0,64) + 0,05∙(-0,09) = 1,13 т∙м.
Построим эпюру нормативных моментов согласно найденным значениям.
Вычислим максимальный расчетный изгибающий момент, действующий на балку
Расчетный изгибающий момент вычисляется аналогично нормативному, только в ходе расчета вместо нормативных значений нагрузок подставляются расчетные.
В итоге расчета у нас получатся следующие значения расчетных моментов:
М1 = 0;
М2 = 0,31 т∙м;
М3 = 1, 3 т∙м;
М4 = 1,3 т∙м;
М5 = 0,31 т∙м;
М6 = 0;
М0 = 1,3 т∙м.
Эпюра расчетных моментов будет следующая:
Определим сечение лобовой балки
По имеющимся данным мы можем подобрать сечение швеллера (см. книгу Я.М. Лихтарников «Расчет стальных конструкций» стр. 60-61 или книгу Васильев А.А. «Металлические конструкции» §24).
Максимальные моменты в сечении балки:
расчетный момент Мр = 1,3 т∙м = 1300 кг∙м;
нормативный момент Мн = 1,13 т∙м = 1130 кг∙м.
Найдем требуемый момент сопротивления для балки:
Wтр = Мр/1,12R = 1300/(1,12∙21) = 55,3 см3. Из сортамента выбираем швеллер №14 (Wх = 70,2 см³; Iх = 491 см4).
Теперь проверим балку на прогиб:
5∙Мн∙L₀/(48EI) = 5∙1130∙240/(48∙21000∙491) = 0,0027 = 1/365 < 1/250 – условие выполняется (здесь 1/250 – максимально допустимый прогиб для балки).
class=»eliadunit»>
Добавить комментарий
Типовые эпюры. Однопролетная шарнирно-опертая балка
Мы уже рассматривали типовые эпюры для консольной балки с статье Типовые эпюры. Консольная балка. Теперь рассмотрим типовые эпюры для однопролетной, шарнирно-опретой балки.
Также как и в прошлой статье рассматривать будем только эпюры Q (поперечная сила), M (изгибающий момент).
Типовые эпюры однопролетной шарнирно-опертой балки
В однопролетной балке оба конца имеют шарнирное закрепление.
Сосредоточенная нагрузка приложена в пролете балки
2-е сосредоточенные нагрузки приложены в пролете балки на равном удалении от опор
Равномерно-распределенная нагрузка по всей длине балки
Равномерно-распределенная нагрузка на участке балки, начинающаяся у одного узла и прерывающаяся в пролете
Равномерно-распределенная нагрузка на участке балки, расположена по центру балки
Переменная нагрузка по всей длине балки
Переменная нагрузка на участке балки, начинающаяся у одного узла и прерывающаяся в пролете
Переменная нагрузка, имеющая максимальную нагрузку в центре балки
Крутящий момент, приложенный в опорном узле балки
Крутящий момент, приложенный в пролете балки
Распределенные нагрузки.
Теоретическая механика
Распределенные нагрузки
Как мы уже знаем, любая сила характеризуется тремя свойствами: модулем (скалярной размерностью), вектором (направлением в пространстве) и точкой приложения. Для того, чтобы иметь полное представление о характере и последствиях воздействия любой силы на тело или элемент конструкции, необходимо знать — какова величина этой силы, куда она направлена и к какой точке приложена.
В действительности сила не может быть приложена к точке, поскольку точка — безразмерная, бесконечно малая единица пространства, поэтому фактически силы воздействуют на очень малую площадку, размерами которой пренебрегают. Такие силы (приложенные к ничтожно малой площадке тела) называют сосредоточенными.
В реальности часто встречаются силы, приложенные не к точке, а к объему или поверхности тела, например сила тяжести, давления ветра, воды и т. п., т. е. нагрузку воспринимает не бесконечно малая площадка, а значительная площадь или объем тела. Такие силы называют распределенными.
Примером распределенной силы (обычно употребляют выражение «распределенная нагрузка») может послужить выпавший на крышу дома снег. Сила тяжести снежного покрова давит на всю поверхность крыши, нагружая одинаково (или неодинаково) каждую единицу ее площади, а не какую-либо точку.
Плоская система распределенных сил характеризуется ее интенсивностью, обычно обозначаемой латинской буквой q.
Интенсивность — это сила, приходящаяся на единицу длины (или площади) нагруженного участка.
Интенсивность в системе единиц СИ выражается в ньютонах на метр (Н/м) или, соответственно, в ньютонах на квадратный метр (для нагрузки, действующей на площадь).
Интенсивность воздействия силы на площадь характеризует такие физические понятия, как давление и напряжение. В плоской системе рассматривается интенсивность действия силы на единицу длины.
Распределенная нагрузка, имеющая постоянную интенсивность по всей длине участка называется равномерно распределенной (см. рисунок 1).
При решении задач статики распределенную нагрузку заменяют ее равнодействующей. Модуль равнодействующей равномерно распределенной нагрузки равен Q = ql (см. рисунок).
Равнодействующая равномерно распределенной нагрузки Q прикладывается в середине отрезка АВ.
Распределенная нагрузка, имеющая переменную интенсивность, называется неравномерно распределенной (рис. 2).
Примером такой нагрузки может служить меняющееся по высоте давление воды на плотину или снег, лежащий на крыше неровным слоем.
Определение точки С приложения равнодействующей неравномерно распределенной нагрузки производится путем геометрических расчетов и построений. Равнодействующая сила Q при таких нагрузках равна площади фигуры, охватываемой эпюрой нагрузки, а точка С приложения равнодействующей расположена в центре тяжести этой фигуры.
Нагрузки, распределенные по поверхности (по площади), характеризуются давлением, т. е. силой, приходящейся на единицу площади. В системе единиц СИ давление измеряется в Паскалях (Па) или ньютонах на квадратный метр (Н/м2).
***
Пример решения задачи с распределенной нагрузкой
Задача: Балка находится в равновесии под действием сосредоточенной силы F = 100 Н и равномерно распределенной нагрузки q = 60 Н/м (см. схему 3).
Необходимо определить реакцию RВ опоры В.
Решение.
Поскольку по условию задачи необходимо определить реакцию опоры В, составим уравнение моментов сил относительно опоры А, учитывая, что равномерно распределенную нагрузку можно заменить сосредоточенной силой:
Q = ql, где l = (10 — 5) метров — часть балки, к которой приложена распределенная нагрузка.
Точка приложения сосредоточенной силы Q расположена в середине той части балки, к которой приложена распределенная нагрузка; плечо этой силы относительно опоры А будет равно: h = (10 — 5)/2 = 2,5 м.
Cоставляем уравнение моментов сил относительно опоры А из условия, что балка находится в состоянии равновесия (уравнение равновесия).
Учитываем знаки:
- сила RВ создает относительно точки А положительный момент, плечо которого равно 10м;
- сила F создает относительно точки А отрицательный момент, плечо которого равно 5 м;
- распределенная нагрузка q создает (посредством силы Q и плеча h) относительно точки А отрицательный момент.
Получаем уравнение равновесия балки, в котором лишь одна неизвестная величина (RВ):
ΣM = 10RВ — qlh — 5F = 10RВ — q(10-5)(10-5)/2 — 5F = 0, откуда находим искомую реакцию опоры RВ:
RВ = {q(10-5)(10-5)/2 + 5F}/10 = 125 Н
Задача решена.
***
Условия равновесия плоской системы сходящихся сил
Распределенная нагрузка — Лекции и примеры решения задач технической механики
Воздействие на детали, конструкции, элементы механизмов может быть задано распределенными нагрузками: в плоской системе задается интенсивность действия по длине конструкции, в пространственной системе – по площади.
Размерность для линейной нагрузки — Н/м, для нагрузки распределенной по площади — Н/м2, для объемной (например при учете собственного веса элементов конструкции) — Н/м3.
Например, на рисунке 1.23, а приведена равномерно распределенная по длине AB нагрузка интенсивностью q, измеряемая в Н/м. Эта нагрузка может быть заменена сосредоточенной силой
Q = q ∙ AB [Н],
приложенной в середине отрезка AB.
На рисунке 1.23, б показана равномерно убывающая (возрастающая) нагрузка, которая может быть заменена равнодействующей силой
Q = qmax∙AB/2,
приложенной в точке C, причем AC = 2/3AB.
В произвольном случае, зная функцию q(x) (рисунок 1.23, в), рассчитываем эквивалентную силу
Эта сила приложена в центре тяжести площади, ограниченной сверху от балки AB линией q(x).
Рисунок 1.23
Примером может служить расчет усилий, разрывающих стенки баллона со сжатым газом. Определим результирующую силу давления в секторе трубы при интенсивности q [Н/м]; R – радиус трубы, 2α – центральный угол, ось Ox – ось симметрии (рисунок 1.24).
Выделим элемент сектора с углом ∆φ и определим силу ∆Q, действующую на плоский элемент дуги:
∆Q = q ∙ ∆l = q ∙ R ∙ ∆φ. (1.14)
Рисунок 1.24
Проекция этой силы на ось Ox будет
∆Qx = q ∙ R ∙ ∆φ∙ cosφ. (1.15)
В силу симметрии элемента трубы (с дугой AB) относительно оси Ox проекция результирующей силы на ось Oy:
Qy = 0, т.е. Q = Qx, (1.16)
где АВ – хорда, стягивающая концы дуги.
Для цилиндрической емкости высотой h и внутренним давлением P на стенки действует нагрузка интенсивностью q = p [Н/м,2]. Если цилиндр рассечен по диаметру (рисунок 1.25), то равнодействующая этих сил равна F = q ∙ d ∙ h (d – внутренний диаметр) или
F = p ∙ 2R ∙ h.
Разрывающие баллон по диаметру усилия:
S1 = S2 = S;
2S = F;
S = p∙h∙R. (1.18)
Рисунок 1.25
Если принять a – толщина стенки, то (пренебрегая усилиями в крышке и дне цилиндра) растягивающее напряжение в стенке равно
>> Уравнения равновесия системы сил
Расчет балки от сосредоточенной нагрузки
Вернуться на страницу «Расчет изгибаемых элементов»
СОСРЕДОТОЧЕННА НАГРУЗКА F
СКАЧАТЬ ФАЙЛ НА GOOGLE.ДИСК
СКАЧАТЬ ФАЙЛ НА ЯНДЕКС.ДИСК
Добавить комментарий Отменить ответ
Ваш e-mail не будет опубликован. Обязательные поля помечены *
Комментарий
Имя *
E-mail *
Сайт
Лимит времени истёк. Пожалуйста, перезагрузите CAPTCHA. × =
Расчет балки. Общие положения — Доктор Лом. Первая помощь при ремонте
1 этап. Определение максимальных напряжений
Внешние силы, действующие на балку, называются нагрузками. Внутренние силы — напряжениями. Тем не менее с точки зрения физики никакой разницы между этими силами нет, поэтому согласно третьему закону Ньютона (сила действия равна силе противодействия и направлена в противоположную сторону) внешние силы можно рассматривать как внутренние и наоборот. На этом основан метод сечений, используемый при расчете балок.
Согласно этому методу, если отсечь часть балки, то для того, чтобы отсеченная часть находилась в состоянии статического равновесия, к полученному сечению балки, как правило поперечному (перпендикулярному нейтральной оси балки), нужно приложить внешние силы. При этом в рассматриваемом сечении будут возникать силы противодействия — напряжения, равные по значению внешним силам и направленные в противоположную сторону.
1.1. Определение видов и количества опор
Опоры у балки могут быть разные: шарнирные и(или) жесткие.
Рисунок 219.2.
Например, у балки, показанной на рисунке 219.2 имеется две вертикальных шарнирных опоры, показанные фиолетовым цветом и одна горизонтальная шарнирная опора, показанная синим цветом.
Как правило опоры обозначаются латинскими литерами А, В, С, D и т.д.
1.2. Определение количества и длины пролетов
Балки могут иметь не только один пролет, но два, три и сколь угодно много. Количество пролетов nп определить не сложно:
nп = nо — 1 (517.1)
где no — количество вертикальных шарнирных опор или жестких заделок.
Балка, показанная на рисунке 219.2, имеет один пролет. Длина пролета l равна расстоянию между вертикальными опорами. Так как действительные опоры балки имеют некоторую ширину, то пролет балки — это расстояние в свету между краями опор. Пролет измеряется в метрах (м).
Если у балки только одна опора — жесткое защемление на конце, то такая балка пролетов не имеет и называется консольной.
1.3. Система координат
При расчете балок используется стандартная система координат с осями х, у и z. Для упрощения расчетов балка рассматривается как стержень, нейтральная ось которого совпадает с осью координат х. При этом начало координат как правило совпадает с началом балки. Соответственно длина балки измеряется по оси х.
Геометрические размеры поперечных сечений балки, т.е. размеры относительно осей y и z, на первом этапе расчетов никакого значения не имеют. Более того именно эти параметры и нужно определить на втором этапе расчета балки на действующие нагрузки.
Таким образом на первом этапе балка рассматривается как некий стержень, размеры сечения которого пренебрежимо малы по сравнению с длиной.
1.4. Определение действующих нагрузок
Все нагрузки, действующие на балку, можно представить в виде:
1.4.1. Сосредоточенных сил
Могут обозначаться как Q, P, N и др. Измеряются в Ньютонах (Н) или килограмм-силах (кгс).
1.4.2. Нагрузок, распределенных по некоторой части длины или по всей длине балки
Как правило такие нагрузки обозначаются литерой q. Измеряются в Н/м или кгс/м.
В свою очередь распределенные нагрузки могут быть равномерно и неравномерно распределенными.
График, показывающий изменение значения распределенной нагрузки по длине балки, называется эпюрой нагрузки. Изменение значения распределенной нагрузки может описываться различными уравнениями. Например, для балки, на которую действует равномерно распределенная нагрузка, эпюра нагрузки имеет вид прямоугольника, а уравнение, описывающее изменение значений нагрузки, имеет следующий вид:
q = const (517.2)
Если одна или несколько нагрузок направлены не перпендикулярно оси х, а под некоторым углом а, то для дальнейших расчетов такие нагрузки разбиваются на вертикальную и горизонтальную составляющие.
Вертикальные составляющие используются для расчета балки на поперечный изгиб. Горизонтальные составляющие используются для определения горизонтальных опорных реакций, а также при необходимости для расчетов на устойчивость сжатого стержня.
Определить значение вертикальных и горизонтальных составляющих нагрузки можно по следующим формулам:
Qв = Qsina (517.3)
Qг = Qcosa (517.4)
где а — угол между осью х и вектором приложения нагрузки. Для распределенных нагрузок используется тот же принцип определения вертикальной и горизонтальной составляющих.
1.4.3. Моментов
Внешний момент, действующий в любой точке по оси х, рассматривается как пара сил, равных по значению и направленных в противоположные стороны. Таким образом значение внешнего момента не зависит от расстояния до какой либо точки по оси х, а только от расстояния между векторами двух противоположно направленных сил.
Примечание: иногда при расчете балок бывает известен угол поворота или перемещение поперечного сечения. По большому счету ни угол поворота, ни перемещение не являются нагрузками, а есть результат воздействия нагрузок. Поэтому в таких случаях перемещения или углы поворота поперечных сечений заменяются силами или моментами, которые вызывают эквивалентное рассматриваемому перемещение или угол поворота.
1.5. Степень статической неопределимости
Все балки с количеством пролетов более одного, являются статически неопределимыми. Но даже и однопролетные балки могут быть статически неопределимыми. Степень статической неопределимости s для балок с шарнирными опорами определяется следующим образом:
sш = nп — 1 (517.5)
Например, для балки, показанной на рисунке 219.2, степень статической неопределимости равна sш = 1 — 1 = 0. Это означает, что такая балка является статически определимой и для ее расчета на первом этапе достаточно трех уравнений статического равновесия системы.
Каждая жесткая заделка добавляет одну степень статической неопределимости. При наличии жестких заделок статическая определимость s определяется следующим образом:
sж = nп + nж — 1 (517.6)
где nж — количество жестких заделок.
Рисунок 145.3.1
Например, для балки, показанной на рисунке 145.3.1, степень статической неопределимости составит sж = 1 + 2 — 1 = 2. Это означает, что для расчета балки на первом этапе потребуется составить два дополнительных уравнения.
1.6. Замена опор опорными реакциями
На этом этапе расчета опоры, имеющиеся у балки, заменяются реактивными силами, получившими название «опорные реакции». Эти опорные реакции также являются внешними силами для балки. Главное отличие опорных реакций от нагрузок в том, что изначально опорные реакции в отличие от нагрузок не известны и их нужно вычислить.
1.7. Статическое равновесие системы
Таким образом, после замены опор на реактивные силы, балка рассматривается как некий стержень, на который действуют внешние силы — нагрузки и опорные реакции. А так как стержень остается в состоянии статического равновесия, то сумма нагрузок равна сумме опорных реакций.
Из этого следуют первые два уравнения статического равновесия системы:
∑Fу = 0 (249.5.1) — для внешних сил, действующих параллельно оси у.
∑Fх = 0 (249.5.2) — для внешних сил, действующих параллельно оси х.
В данном случае F — это общее обозначение для внешних сил: и нагрузок и опорных реакций.
Третье уравнение статического равновесия применимо только для статически определимых балок с шарнирными опорами. Смысл его сводится к тому, что шарнирные опоры не препятствуют повороту стержня на опоре, а значит момент на такой опоре будет равен нулю, если балка бесконсольная. Если на консоль действует нагрузка, то момент на опоре определяется, как для обычной консольной балки.
Для бесконсольной балки третье уравнение статического равновесия будет иметь вид:
∑МА = ΣМВ = 0 (517.7).
Примечание: В данном случае моменты — это произведение рассматриваемых сил на плечо действия.
Если нагрузка распределена по длине балки, то сначала определяется суммарная нагрузка (площадь грузовой эпюры), при этом плечо действия равно расстоянию от центра тяжести эпюры нагрузки. Другими словами, сначала распределенная нагрузка приводится к сосредоточенной силе и эта условно сосредоточенная сила действует в центре тяжести эпюры нагрузки.
1.8. Определение опорных реакций
Используя уравнения статического равновесия системы, можно сразу определить опорные реакции для статически определимой балки. Сначала с помощью уравнения (517.7) определяется одна вертикальная опорная реакция, а потом с помощью уравнения (249.5.1) — вторая вертикальная опорная реакция. При наличии горизонтальных составляющих нагрузки при помощи уравнения (249.5.2) определяется горизонтальная опорная реакция.
При расчете статически неопределимых балок сначала определяются значения опорных реакций на промежуточных шарнирных опорах, если используется метод нулевых перемещений на опорах (метод сил) или моменты на промежуточных шарнирных или крайних жестких опорах, если используется метод определения углов поворота на опорах (уравнения трех моментов).
При использовании уравнений трех моментов значение реакции на крайней опоре А определяется, исходя из условия:
А = (МВ + Мн)/l (517.8)
где МВ — значение момента на опоре В, определенное с помощью уравнений трех моментов. Мн — значение момента на опоре В от действующей нагрузки. Для остальных опор уравнения составляются по такому же принципу и только для крайней опоры используется одно из уравнений статического равновесия.
1.9. Построение эпюр
После того, как определены значения опорных реакций, можно переходить непосредственно к определению напряжений в поперечных сечениях балки. Для этого строятся эпюры поперечных и продольных сил, эпюра моментов, углов поворота поперечных сечений и эпюра перемещений (прогибов).
Физический смысл эпюр в том, что они показывают изменение указанных параметров в поперечных сечениях по длине балки. Таким образом эпюры являются графиками, описывающими решение соответствующих уравнений. Примеры эпюр поперечных сил и изгибающих моментов при действии различных видов нагрузки для статически определимых балок можно посмотреть здесь, а для некоторых видов статически неопределимых балок — тут.
Затем по эпюре моментов определяется самое нагруженное поперечное сечение балки, в этой точке на эпюре моментов максимальное значение, отрицательное или положительное, в данном случае не имеет значения. Затем для этого сечения определяются значения поперечных и нормальных сил по соответствующим эпюрам.
2 этап. Подбор сечения
Так как разные материалы имеют разные значения расчетных сопротивлений, то соответственно и требуемые параметры сечения для балок из различных материалов будут разными.
2.1. Определение материала балки и расчетного сопротивления материала
После того, как выбран материал для балки, определяются расчетные сопротивления материала изгибу Rи, сжатию Rc, растяжению Rр и т.п. по действующим нормативным документам или по данным производителя, если балка будет из стали.
Для балок из разнородных материалов сначала определяются параметры приведенного сечения. Суть приведенного сечения состоит в том, что рассматривается некое условное сечение материала обладающего равным сопротивлением, при этом ширина сечения для материала, обладающего большим расчетным сопротивлением увеличивается во столько раз, во сколько расчетное сопротивление одного материала больше расчетного сопротивления другого материала. Поэтому такое сечение и называется приведенным. Другими словами, если бы балка изготавливалась из одного материала, то именно так и должно было бы выглядеть поперечное сечение.
Для железобетонных балок, являющихся также балками из разнородных материалов, как правило в процессе расчета требуется дополнительно определить сечение арматуры. Возможные варианты расчета железобетонных балок рассмотрены отдельно.
2.2. Определение требуемого момента сопротивления
Требуемый момент сопротивления определяется, исходя из следующего условия:
Wтр ≥ М/Rиγs (149.4.8)
где М — максимальное значение изгибающего момента, определенного по эпюре моментов, построенной относительно оси х. γs — коэффициент условий работы.
Момент сопротивления измеряется в см3.
2.3. Определение геометрических параметров сечения
2.3 Определение геометрических параметров сечения
Поперечное сечение балки может быть каким угодно: круглым, квадратным, прямоугольным, в виде швеллера, двутавра, круглой или прямоугольной трубы и т.д.
Как известно наиболее оптимальными являются сечения в виде двутавра, швеллера или квадратной трубы, именно такие сечения и принимаются для стальных балок.
Для деревянных балок чаще используются прямоугольные и круглые сечения. И хотя круглое сечение саме неэффективное с точки зрения использования материала, однако бревна — самый дешевый строительный материал, так как требуют минимум предварительной обработки при изготовлении балок. Тем не менее, при достаточно больших пролетах и нагрузках деревянные клеенные балки двутаврового сечения также имеют место.
Для железобетонных балок наиболее характерны прямоугольное и тавровое сечения. Впрочем, как уже говорилось, расчет железобетонных балок отличается от расчета обычных балок.
Для балок прямоугольного сечения требуемая высота сечения определяется по формуле:
(147.4)
Для стальных балок все значительно проще — момент сопротивления принимаемого профиля, определяемой по соответствующему сортаменту, должен быть не меньше требуемого момента сопротивления, определенного по формуле (149.4.8)
2.4. Определение прогиба
Так как для однопролетных балках на шарнирных опорах значение прогиба часто является определяющим, то я рекомендую определять прогиб сразу после определения параметров сечения.
Формулы для определения прогиба и углов поворота сечения на опорах зависят от вида приложенной к балке нагрузки. Значение модуля упругости E для выбранного материала балки определяется по нормативным документам, здесь можно посмотреть примерные значения модулей упругости для некоторых строительных материалов. Значение момента инерции I определяется в зависимости от геометрической формы сечения или по сортаменту для стальных балок из прокатного профиля.
Если прогиб f, определенный по одной из вышеуказанных формул, меньше допустимого нормативными документами, в частности СП 20.13330.2011 «Нагрузки и воздействия», то можно продолжать расчеты. Если прогиб больше допустимого, то сначала следует подобрать сечение, обеспечивающее требования по прогибу. Например для балки, на которую действует равномерно распределенная нагрузка, значение момента инерции можно определить по следующей формуле:
I = 5ql4/(384Ef) (517.9)
2.5. Проверка на прочность опорных участков балки
Любая балка в отличие от показанной на рисунке 219.2 модели имеет опорные участки. На этих опорных участках действуют нормальные напряжения в сечениях, параллельных нейтральной оси балки. В общем случае (если балка прямоугольная и напряжения на опорном участке равномерно изменяются от максимума до нуля) эти напряжения определяются по следующей формуле:
σу = 2Q/(blоп) ≤ Rcγs (517.10)
где Q — значение поперечной силы согласно эпюры «Q», b — ширина балки, lоп — длина опорного участка, 2 — коэффициент учитывающий неравномерность распределения напряжений на опорном участке. Rc — расчетное сопротивление сжатию.
2.5.1. Проверка на прочность в местах действия сосредоточенной нагрузки
Так как на балку может действовать не только распределенная нагрузка, но и одна или несколько сосредоточенных нагрузок, то места действия сосредоточенных нагрузок также следует проверить на прочность.
В данном случае формула для определения нормальных напряжений будет будет почти такой же как (517.10), вот только значение коэффициента, учитывающего неравномерность распределения нагрузки, будет зависеть от того, как именно сосредоточенная нагрузка передается рассчитываемой балке.
Например, если рассчитываемая балка будет находиться посредине помещения и на нее сверху будет опираться второстепенная балка, то значение коэффициента будет равно 1.
2.6. Проверка по касательным напряжениям
В поперечных сечениях, соответствующих опорным точкам балки, а также в сечениях, параллельных нейтральной оси балки, будут действовать касательные напряжения, которые не должны превышать расчетного сопротивления Rs сдвигу или сколу:
т = QySzотс/bIz ≤ Rsγs (270.2)
Подобная проверка особенно важна для стальных тонкостенных балок.
2.7. Определение максимальных напряжений
Если в рассматриваемой точке (точнее на грани параллелепипеда с рассматриваемой точкой на одной из граней) действуют и нормальные и касательные напряжения, то возникает плоское напряженное состояние.
В этом случае необходимо определить максимальное нормальное напряжение, действующее в этой точке, другими словами определить главные площадки напряжений. Для этого используется одна из теорий прочности. Так, согласно третьей теории прочности:
σпр =(σ2 +4т2)0.5 ≤ R (517.11)
Если на 4 из 6 главных площадок напряжений в области рассматриваемой точки действуют нормальные и касательные напряжения (например в местах приложения сосредоточенных нагрузок или на промежуточных опорах многопролетных балок), то значение максимальных нормальных напряжений составит:
σпр = ((σх — σу)2 + 4тху2)0.5 ≤ R (517.12)
Эта формула следует из общих положений теории сопротивления материалов, однако для стальных балок нормативные документы требуют проводить расчет по несколько другой формуле.
Кроме того в некоторых случаях, если отсутствуют опорные связи из плоскости балки (что в малоэтажном строительстве встречается крайне редко) тонкостенные стальные балки открытого профиля, а также деревянные балки любого сечения следует проверить на устойчивость в сжатой зоне сечения, но это уже совсем другая история.
Вот собственно и все, что имеет отношение к расчету балок.
Нормативная нагрузка на вспомогательную балку
qn = a2(pn + gn,н + gn,бн) = 3 (12,55 + 0,628 + 0,114) = 39,88 кН/м.
Расчетная нагрузка
q = a2(pnγfp + gn,нγfg + gn,бнγfg) =
= 3 (12,55 · 1,2 + 0,628 · 1,05 + 0,114 · 1,05) = 47,52 кН/м.
Расчетный изгибающий момент
Mmax = ql2/8 = 47,52 ∙ 62 / 8 = 213,84 кН∙м.
Максимальная поперечная сила у опоры
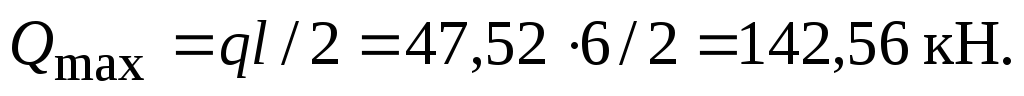
Требуемый момент сопротивления
Wn,min = Mmax/(cxβRyγc) = 21384 / (1,12 · 1 · 24 · 1) = 795,54 см3,
По сортаменту выбираем ближайший номер двутавра, у которого Wx > Wn,min. Принимаем I40, имеющий момент сопротивления Wx = 953 см3; момент инерции сечения Ix = 19062 см4; статический момент полусечения Sx = 545 см3;площадь сечения А = 72,6 см2; ширину пояса bf = 155 мм; толщину пояса tf = 13 мм; толщину стенки tw = 8,3 мм; радиус внутреннего закругления R = 15 мм; линейную плотность (массу 1 м пог.) 57 кг.
Уточнение коэффициента сx, M и Q с учетом собственного веса вспомогательной балки.
Площадь пояса

Площадь стенки
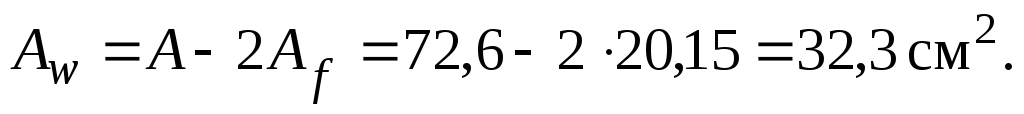
Отношение Af /Aw = 20,15 / 32,3 = 0,62.
По табл. 4.2 определяем коэффициент сx= 1,108.
Равномерно распределенная нагрузка от собственного веса вспомогательной балки
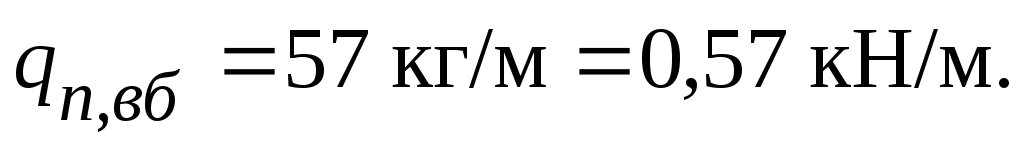
Нормативная нагрузка на вспомогательную балку
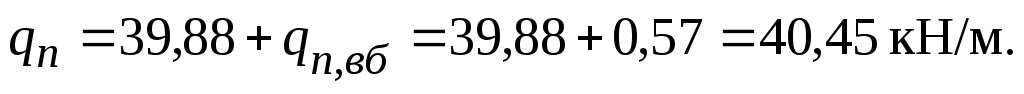
Расчетная нагрузка
q = 47,52 + qn,вбγfg = 47,52 + 0,57 ∙ 1,05 = 48,12 кН/м.
Расчетный изгибающий момент
Mmax = ql2/8 = 48,12 · 62 / 8 = 216,54 кН∙м.
Поперечная сила

Проверка несущей способности балки.Проверка прочности по нормальным напряжениям в середине балки:
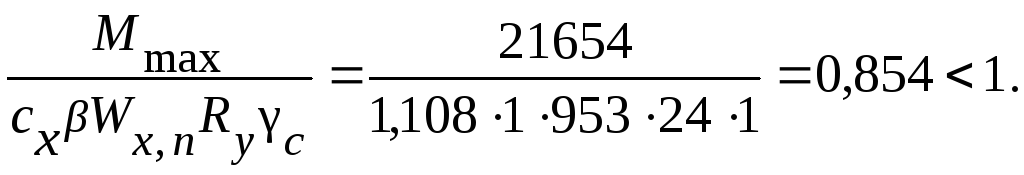
Резерв несущей способности
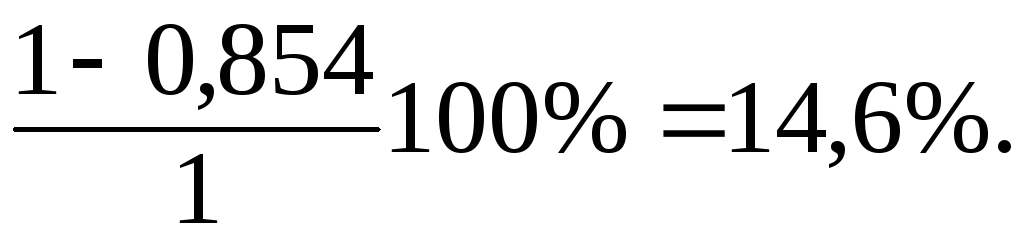
Несмотря на большое недонапряжение сечение принято, так как при изменении сечения в меньшую сторону, принимая ближайший профиль I36 с Wx= 743 см3, перенапряжение составит 9%.
Проверка прочности по касательным напряжениям вблизи опоры:

В местах приложения локальной нагрузки к верхнему поясу (рис. 4.9), а также в опорных сечениях балки, не укрепленных ребрами жесткости, стенку следует дополнительно проверить на местное напряжение σlocпо формуле
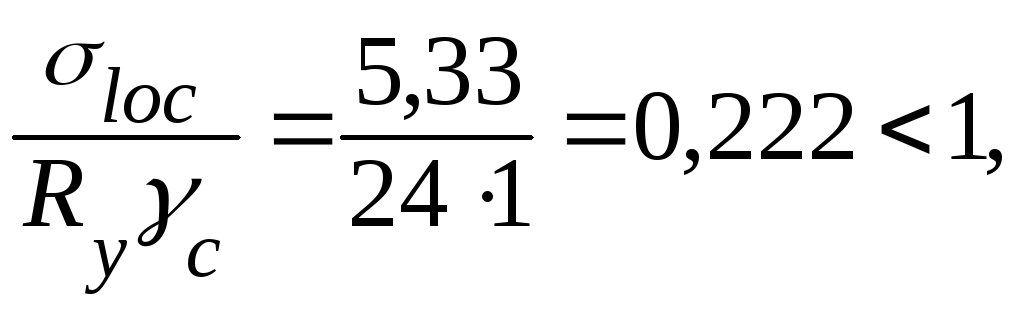
где σloc=F/(lef tw) = 57,04 / (12,9 · 0,83) = 5,33 кН/см2,
здесь F = 2Q = 2 · 28,52 = 57,04 кН – расчетное значение сосредоточенной силы, равное двум реакциям от балок настила;
lef = b + tf′= 7,3 + 2 · 2,8 = 12,9 см –условная длина распределения сосредоточенной нагрузки на стенку вспомогательной балки;
b= 73 мм – ширина пояса балки настила;
t‘f =tf+R= 13 + 15 = 28 мм – расстояние от наружной грани полки до начала внутреннего закругления стенки.
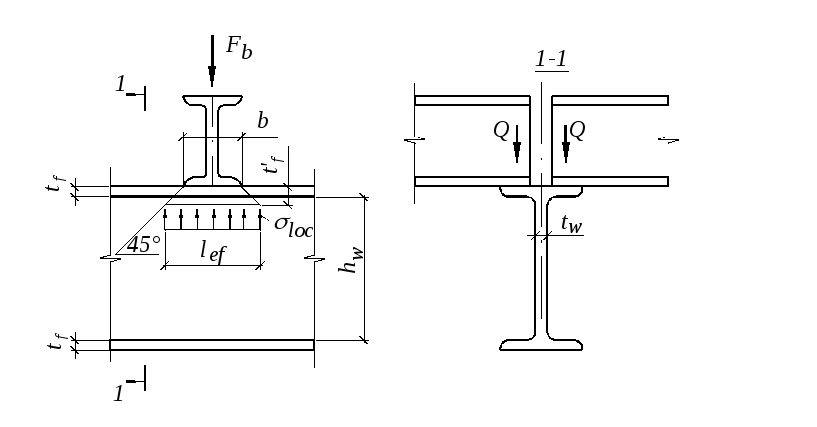
Рис. 4.9.Схема распределения сосредоточенной нагрузки
На стенку прокатной балки
Общую устойчивость вспомогательных балок проверять не надо, поскольку их сжатые пояса надежно закреплены в горизонтальном направлении часто расположенными и приваренными к ним балками настила.
Проверка жесткости.Прогибы, определяемые от нормативных нагрузок, не должны превышать их предельных значений, установленных нормами проектирования. Для однопролетной балки, нагруженной равномерно распределенной нагрузкой, проверка прогиба производится по формуле

где fu=l/250 = 2,4 см при пролетеl = 6 м (см. табл. 4.1).
Принятое сечение удовлетворяет условиям прочности и жесткости.
Определяем вес вспомогательной балки на 1м2 рабочей площадки:

