Расстояние от точки до прямой на плоскости — Википедия
Расстояние от точки до прямой на плоскости — это кратчайшее расстояние от точки до прямой в евклидовой геометрии. Расстояние равно длине отрезка, который соединяет точку с прямой и перпендикулярен прямой. Формула вычисления расстояния может быть получена и выражена несколькими способами.
Знание наименьшего расстояния от точки до прямой может быть полезно во многих случаях, например, для поиска кратчайшего пути для выхода на дорогу, определение разброса графа, и подобное. В регрессии Деминга, процедуре линейного сглаживания, если зависимые и независимые переменные имеют одну и ту же дисперсию, регрессия сводится к ортогональной регрессии, в которой степень приближения измеряется для каждой точки как расстояние от точки до регрессионной прямой.
Прямая задана уравнением[править | править код]
Когда прямая на плоскости задана уравнением ax + by + c = 0, где a, b и c — такие вещественные константы, что a и b не равны нулю одновременно, и расстояние от прямой до точки (
- distance(ax+by+c=0,(x0,y0))=|ax0+by0+c|a2+b2.{\displaystyle \operatorname {distance} (ax+by+c=0,(x_{0},y_{0}))={\frac {|ax_{0}+by_{0}+c|}{\sqrt {a^{2}+b^{2}}}}.}
Точка на прямой, наиболее близкая к (x0,y0), имеет координаты [2]
- x=b(bx0−ay0)−aca2+b2{\displaystyle x={\frac {b(bx_{0}-ay_{0})-ac}{a^{2}+b^{2}}}} и y=a(−bx0+ay0)−bca2+b2.{\displaystyle y={\frac {a(-bx_{0}+ay_{0})-bc}{a^{2}+b^{2}}}.}
Горизонтальные и вертикальные прямые
В общем уравнении прямой ax + by + c = 0 коэффициенты a и b не могут быть одновременно равны нулю пока c ненулевое, а в случае всех нулевых коэффициентов уравнение не задаёт прямую. Если a = 0, а b ≠ 0, прямая горизонтальна и имеет уравнение y = —c/b. Расстояние от (x0, y0) до этой прямой определяется вертикальным отрезком длины |y0 — (-c/b)| = |by0 + c| / |b| (согласно формуле). Аналогичным образом, для вертикальных прямых (b = 0) расстояние между той же точкой и прямой равно |ax0 + c| / |a| и измеряется вдоль горизонтального отрезка.
Нормированное уравнение прямой
Нормированное уравнение прямой — это уравнение вида
- xcosα+ysinα−p=0{\displaystyle x\cos \alpha +y\sin \alpha -p=0}
Нормированное уравнение получается из общего уравнения прямой ax + by + c = 0 делением всех членов на a2+b2{\displaystyle {\sqrt {a^{2}+b^{2}}}}. Тогда расстояние от точки (x0, y0) до прямой равно абсолютному значению отклонения и вычисляется по формуле [3][4]
- |d|=|x0cosα+y0sinα−p|{\displaystyle |d|=|x_{0}\cos \alpha +y_{0}\sin \alpha -p|}
Прямая задана двумя точками[править | править код]
Если прямая проходит через две точки P1=(x1,y1) и P2=(x2,y2), то расстояние от (x0,y0) до прямой равно:
- distance(P1,P2,(x0,y0))=|(y2−y1)x0−(x2−x1)y0+x2y1−y2x1|(y2−y1)2+(x2−x1)2.{\displaystyle \operatorname {distance} (P_{1},P_{2},(x_{0},y_{0}))={\frac {|(y_{2}-y_{1})x_{0}-(x_{2}-x_{1})y_{0}+x_{2}y_{1}-y_{2}x_{1}|}{\sqrt {(y_{2}-y_{1})^{2}+(x_{2}-x_{1})^{2}}}}.}
Знаменатель этого выражения равен расстоянию между точками P1 и P2. Числитель равен удвоенной площади треугольника с вершинами (x0,y0), P1 и P2 (см. Общая формула площади треугольника в декартовых координатах). Выражение эквивалентно h=2Ab{\textstyle h={\frac {2A}{b}}}, что может быть получено преобразованием стандартной формулы площади треугольника: A=12bh{\textstyle A={\frac {1}{2}}bh}, где b — длина стороны, а h — высота на эту сторону из противолежащей вершины.
Алгебраическое доказательство[править | править код]
Это доказательство верно, только когда прямая не является ни вертикальной, ни горизонтальной. То есть мы предполагаем, что ни a, ни b в уравнении не равны нулю.
Прямая с уравнением ax + by + c = 0 имеет наклон —a/b, так что любая прямая, перпендикулярная к заданной, имеет наклон b/a. Пусть (m, n) — точка пересечения прямой ax + by + c = 0 и перпендикулярной прямой, проходящей через точку (x0, y0). Прямая, проходящая через эти две точки, перпендикулярна исходной прямой, так что
- y0−nx0−m=ba.{\displaystyle {\frac {y_{0}-n}{x_{0}-m}}={\frac {b}{a}}.}
Таким образом, a(y0−n)−b(x0−m)=0,{\displaystyle a(y_{0}-n)-b(x_{0}-m)=0,} и после возведения в квадрат получим:
- a2(y0−n)2+b2(x0−m)2=2ab(y0−n)(x0−m).{\displaystyle a^{2}(y_{0}-n)^{2}+b^{2}(x_{0}-m)^{2}=2ab(y_{0}-n)(x_{0}-m).}
Рассмотрим,
- (a(x0−m)+b(y0−n))2=a2(x0−m)2+2ab(y0−n)(x0−m)+b2(y0−n)2=(a2+b2)((x0−m)2+(y0−n)2){\displaystyle (a(x_{0}-m)+b(y_{0}-n))^{2}=a^{2}(x_{0}-m)^{2}+2ab(y_{0}-n)(x_{0}-m)+b^{2}(y_{0}-n)^{2}=(a^{2}+b^{2})((x_{0}-m)^{2}+(y_{0}-n)^{2})}
Здесь использовано возведённое в квадрат выражение. Но
- (a(x0−m)+b(y0−n))2=(ax0+by0−am−bn)2=(ax0+by0+c)2{\displaystyle (a(x_{0}-m)+b(y_{0}-n))^{2}=(ax_{0}+by_{0}-am-bn)^{2}=(ax_{0}+by_{0}+c)^{2}},
так как точка (m, n) расположена на прямой ax + by + c = 0. Таким образом,
- (a2+b2)((x0−m)2+(y0−n)2)=(ax0+by0+c)2{\displaystyle (a^{2}+b^{2})((x_{0}-m)^{2}+(y_{0}-n)^{2})=(ax_{0}+by_{0}+c)^{2}}
Из этого получаем длину отрезка между этими двумя точками:
- d=(x0−m)2+(y0−n)2=|ax0+by0+c|a2+b2.{\displaystyle d={\sqrt {(x_{0}-m)^{2}+(y_{0}-n)^{2}}}={\frac {|ax_{0}+by_{0}+c|}{\sqrt {a^{2}+b^{2}}}}.} [5].
Геометрическое доказательство[править | править код]
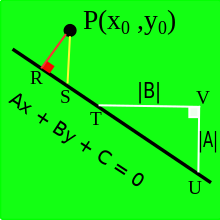
Это доказательство верно, только когда прямая не является ни вертикальной, ни горизонтальной. Баллантин и Джерберт[6] не упомянули это ограничение в своей статье.
Опустим перпендикуляр из точки P с координатами (x0, y0) на прямую с уравнением Ax + By + C = 0. Обозначим основание перпендикуляра буквой R. Проведём вертикальную прямую через P и обозначим пересечение этой вертикальной прямой с исходной прямой буквой S. В произвольной точке T на прямой нарисуем прямоугольный треугольник TVU, катеты которого являются горизонтальными и вертикальными отрезками, а длина горизонтального отрезка равна |B| (см. рисунок). Вертикальный катет треугольника ∆TVU будет иметь длину |A|, поскольку наклон прямой равен —A/B.
Треугольники ∆SRP и ∆UVT подобны, так как они оба прямоугольные и ∠PSR ≅ ∠VUT, поскольку являются соответственными углами двух параллельных прямых PS и UV (вертикальные прямые) и секущей (исходная прямая)[7]. Выпишем отношения сторон этих треугольников:
- |PR¯||PS¯|=|TV¯||TU¯|.{\displaystyle {\frac {|{\overline {PR}}|}{|{\overline {PS}}|}}={\frac {|{\overline {TV}}|}{|{\overline {TU}}|}}.}
Если точка S имеет координаты (x0,m), то |PS| = |y0 — m| и расстояние от P до прямой равно:
- |PR¯|=|y0−m||B|A2+B2.{\displaystyle |{\overline {PR}}|={\frac {|y_{0}-m||B|}{\sqrt {A^{2}+B^{2}}}}.}
Поскольку S находится на прямой, мы можем найти значение m,
- m=−Ax0−CB,{\displaystyle m={\frac {-Ax_{0}-C}{B}},}
и получаем: [6]
- |PR¯|=|Ax0+By0+C|A2+B2.{\displaystyle |{\overline {PR}}|={\frac {|Ax_{0}+By_{0}+C|}{\sqrt {A^{2}+B^{2}}}}.}
Другой вариант этого доказательства — поместить точку V в точку P и вычислить площадь треугольника ∆UVT двумя способами, после чего получим D|TU¯|=|VU¯||VT¯|{\displaystyle D|{\overline {TU}}|=|{\overline {VU}}||{\overline {VT}}|}, где D — высота треугольника ∆UVT на гипотенузу из точки P. Формула расстояния может быть использована, чтобы выразить |TU¯|{\displaystyle |{\overline {TU}}|}, |VU¯|{\displaystyle |{\overline {VU}}|} и |VT¯|{\displaystyle |{\overline {VT}}|}в терминах координат P и коэффициентов уравнения исходной прямой, в результате чего получим требуемую формулу.
Доказательство с помощью проекции вектора[править | править код]
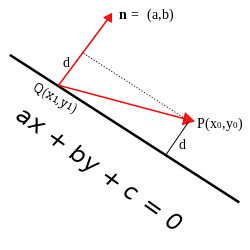
Пусть P — точка с координатами (x0, y0) и пусть исходная прямая имеет уравнение ax + by + c = 0. Пусть Q = (x1, y1) — любая точка на прямой и n — вектор (a, b) с началом в точке Q. Вектор n перпендикулярен прямой, и расстояние d от точки P до прямой равно длине ортогональной проекции QP→{\displaystyle {\overrightarrow {QP}}} на n. Длина этой проекции равна:
- d=|QP→⋅n|‖n‖.{\displaystyle d={\frac {|{\overrightarrow {QP}}\cdot \mathbf {n} |}{\|\mathbf {n} \|}}.}
Теперь
- QP→=(x0−x1,y0−y1),{\displaystyle {\overrightarrow {QP}}=(x_{0}-x_{1},y_{0}-y_{1}),} так что QP→⋅n=a(x0−x1)+b(y0−y1){\displaystyle {\overrightarrow {QP}}\cdot \mathbf {n} =a(x_{0}-x_{1})+b(y_{0}-y_{1})} и ‖n‖=a2+b2.{\displaystyle \|\mathbf {n} \|={\sqrt {a^{2}+b^{2}}}.}
Тогда
- d=|a(x0−x1)+b(y0−y1)|a2+b2.{\displaystyle d={\frac {|a(x_{0}-x_{1})+b(y_{0}-y_{1})|}{\sqrt {a^{2}+b^{2}}}}.}
Поскольку Q лежит на прямой, c=−ax1−by1{\displaystyle c=-ax_{1}-by_{1}}, а тогда [8][9][10]
- d=|ax0+by0+c|a2+b2.{\displaystyle d={\frac {|ax_{0}+by_{0}+c|}{\sqrt {a^{2}+b^{2}}}}.}
Можно получить другие выражения для кратчайшего расстояния от точки до прямой. Эти выводы тоже требуют, чтобы прямая не была вертикальной или горизонтальной.
Пусть точка P задана координатами (x0,y0{\displaystyle x_{0},y_{0}}). Пусть прямая задана уравнением y=mx+k{\displaystyle y=mx+k}. Уравнение прямой, перпендикулярной исходной прямой и проходящей через точку P, задаётся уравнением y=x0−xm+y0{\displaystyle y={\frac {x_{0}-x}{m}}+y_{0}}.
Точка, в которой эти две прямые пересекаются, является ближайшей точкой на исходной прямой для точки P. Тогда:
- mx+k=x0−xm+y0.{\displaystyle mx+k={\frac {x_{0}-x}{m}}+y_{0}.}
Мы можем решить это уравнение по x,
- x=x0+my0−mkm2+1.{\displaystyle x={\frac {x_{0}+my_{0}-mk}{m^{2}+1}}.}
Координату y точки пересечения можно найти, подставив значение x в уравнение исходной прямой,
- y=m(x0+my0−mk)m2+1+k.{\displaystyle y=m{\frac {(x_{0}+my_{0}-mk)}{m^{2}+1}}+k.}
Подставив полученные значения в формулу расстояния d=(X2−X1)2+(Y2−Y1)2{\displaystyle d={\sqrt {(X_{2}-X_{1})^{2}+(Y_{2}-Y_{1})^{2}}}}, получим формулу кратчайшего расстояния от точки до прямой:
- d=(x0+my0−mkm2+1−x0)2+(mx0+my0−mkm2+1+k−y0)2.{\displaystyle d={\sqrt {\left({{\frac {x_{0}+my_{0}-mk}{m^{2}+1}}-x_{0}}\right)^{2}+\left({m{\frac {x_{0}+my_{0}-mk}{m^{2}+1}}+k-y_{0}}\right)^{2}}}.}
Если заметить, что m = —a/b и k = —c/b для уравнения ax + by + c = 0, после небольших выкладок получим стандартное выражение[2].
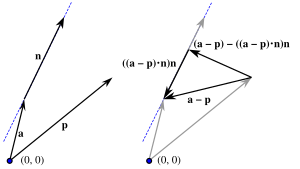Иллюстрация формулировки с помощью векторов.Запишем прямую в векторном виде:
- x=a+tn{\displaystyle \mathbf {x} =\mathbf {a} +t\mathbf {n} },
где x — вектор, задающий координаты любой точки на прямой, n — единичный вектор в направлении прямой, a — вектор, задающий две координаты точки на прямой, а t — скаляр. То есть для получения точки x на прямой начинаем с точки a на прямой и двигаемся на расстояние t вдоль прямой.
Расстояние от произвольной точки p до прямой задаётся формулой
- distance(x=a+tn,p)=‖(a−p)−((a−p)⋅n)n‖.{\displaystyle \operatorname {distance} (\mathbf {x} =\mathbf {a} +t\mathbf {n} ,\mathbf {p} )=\|(\mathbf {a} -\mathbf {p} )-((\mathbf {a} -\mathbf {p} )\cdot \mathbf {n} )\mathbf {n} \|.}
Эта формула геометрически строится следующим образом: a−p{\displaystyle \mathbf {a} -\mathbf {p} } — это вектор из p в точку a на прямой. Тогда (a−p)⋅n{\displaystyle (\mathbf {a} -\mathbf {p} )\cdot \mathbf {n} } — это длина проекции на прямую, а тогда
- ((a−p)⋅n)n{\displaystyle ((\mathbf {a} -\mathbf {p} )\cdot \mathbf {n} )\mathbf {n} }
— это вектор, являющийся проекцией a−p{\displaystyle \mathbf {a} -\mathbf {p} } на прямую. Тогда
- (a−p)−((a−p)⋅n)n{\displaystyle (\mathbf {a} -\mathbf {p} )-((\mathbf {a} -\mathbf {p} )\cdot \mathbf {n} )\mathbf {n} }
является компонентой вектора a−p{\displaystyle \mathbf {a} -\mathbf {p} }, перпендикулярной прямой. Следовательно, расстояние от точки до прямой равно норме этого вектора[11]. Эта формула может быть использована и в более высоких размерностях.
Другая формулировка с помощью векторов[править | править код]
Если векторное пространство ортонормально, а прямая (d ) проходит через точку B и имеет вектор направления[en] u→{\displaystyle {\vec {u}}}, то расстояние от точки A до прямой (d) равно
- d(A,(d))=‖BA→∧u→‖‖u→‖{\displaystyle d(\mathrm {A} ,(d))={\frac {\left\|{\overrightarrow {\mathrm {BA} }}\wedge {\vec {u}}\right\|}{\|{\vec {u}}\|}}},
где BA→∧u→{\displaystyle {\overrightarrow {\mathrm {BA} }}\wedge {\vec {u}}} — векторное произведение векторов BA→{\displaystyle {\overrightarrow {\mathrm {BA} }}} и u→{\displaystyle {\vec {u}}}, а ‖u→‖{\displaystyle \|{\vec {u}}\|} — норма вектора u→{\displaystyle {\vec {u}}}.
- ↑ Larson, Hostetler, 2007, p. 452.
- ↑ 1 2 Larson, Hostetler, 2007, p. 522.
- ↑ Привалов, 1966, с. 67.
- ↑ Делоне, Райков, 1948, с. 195.
- ↑ Laudanski, 2014.
- ↑ 1 2
- ↑ Если два треугольника окажутся по разные стороны от исходной прямой, эти углы будут накрест лежащими, а потому опять равными.
- ↑ Anton, 1994, с. 138-9.
- ↑ Федотов, Карпов, 2005, с. 86.
- ↑ Моденов, 1967, с. 152.
- ↑ Sunday, Dan. Lines and Distance of a Point to a Line (неопр.). // softSurfer. Дата обращения 6 декабря 2013.
- Делоне Б. Н., Райков Д. А. . Аналитическая геометрия. T. 1. — М., Л.: ОГИЗ, 1948. — 456 с.
- Моденов П. С. . Аналитическая геометрия. — М.: Изд-во Моск. ун-та, 1967. — 697 с.
- Привалов И. И. . Аналитическая геометрия. 13-е изд. — М.: Наука, 1966. — 272 с.
- Федотов А. Г., Карпов Б. В. . Аналитическая геометрия. — М.: МГИЭМ, 2005. — 158 с. — ISBN 5-94506-116-6.
- Anton H. . Elementary Linear Algebra. 7th ed. — Somerset: John Wiley & Sons, 1994. — ISBN 0-471-58742-7.
- Ballantine J. P., Jerbert A. R. Distance from a Line or Plane to a Point // American Mathematical Monthly. — 1952. — Vol. 59. — P. 242—243. — DOI:10.2307/2306514.
- Larson R., Hostetler R. . Precalculus: A Concise Course. — Boston: Houghton Mifflin, 2007. — xvii + 526 + 102 p. — ISBN 0-618-62719-7.
- Laudański L. M. . Between Certainty and Uncertainty: Statistics and Probability in Five Units with Notes on Historical Origins and Illustrative Numerical Examples. — Berlin; Heidelberg: Springer Verlag, 2014. — x + 318 p. — (Intelligent Systems Reference Library, vol. 31). — ISBN 978-3-642-25696-7.
|
Как записывается «расстояние между прямыми»? Сойдет ли, например, $% \rho(AB; CD) $% в записи решения как расстояние между AB и CD? student Я думаю, тут нет единого общепринятого стандарта обозначения. Поэтому в описании, если оно требуется, его можно ввести, предварительно сказав, что символом $%\rho$% (или $%d$%) будет обозначаться расстояние между двумя прямыми или фигурами более общего вида. Иногда в таких случаях пишут что-то вроде $%dist$%, но, вообще говоря, всё годится. @falcao, просто мне интересно, как это записать, например, в блоке «Дано» стереометрической задачи на ЕГЭ. Думаю, проверяющие поймут эту запись. .. Олимпиады намного лучше ЕГЭ уже в плане оформления: главное — не записать «Дано», а найти идею решения. Я считаю, что любое обозначение, не являющееся стопроцентно общепринятым и стандартным, нужно пояснять словами. Это как бы «правило хорошего тона». Конечно, при использовании «естественных» обозначений есть надежда, что смысл будет понят и так, но в принципе могут и «придраться». Поэтому я бы «во избежание» всегда придерживался указанного выше принципа. %COMMENT% |
Угловое расстояние — Википедия
Материал из Википедии — свободной энциклопедии
В математике (в частности, в геометрии и тригонометрии) и во всех естественных науках (например, в астрономии и геофизике) угловое расстояние — это мера видимого расстояния между двумя точками или объектами, выраженная в угловых единицах дуги, при условии, что наблюдатель находится в вершине угла концами которого являются две рассматриваемые точки. Угловой диаметр является частным случаем углового размера.
Угловое расстояние является фундаментальной величиной в астрономии, определяющей положение любого объекта на небесной сфере по его небесным координатам: либо в угловых единицах, либо во времени. Азимут, высота, склонение или прямое восхождение объекта на небе, среди прочего, являются небесными координатами. Любое из них — это угловое расстояние до точки или плоскости отсчета: горизонта, небесного экватора, меридиана и т. д.
Термин угловое расстояние технически синонимичен самому углу, но предназначен для обозначения линейного расстояния (часто огромного и неизвестного) между этими объектами (например, звездами, наблюдаемыми с Земли).
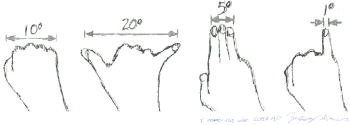
Для визуальных наблюдений без претензий на точность можно вычислить угловое расстояние, конечно, с приближениями порядка степени, и, конечно, очень грубо.
Отдельные вариации — длина руки, толщина пальцев и т. д. — меняют значения в первых приближениях, но не так важны для определения местоположения звезды или планеты, видимой невооруженным глазом или для связи созвездия с соседями.
Поскольку угловое расстояние концептуально совпадает с углом, оно измеряется в тех же единицах, например, градусах или радианах и с использованием таких приборов, как гониометры или оптические приборы, специально предназначенные для поворота в четко определенных направлениях и записи соответствующих углов (такие как телескопы).
Чтобы рассчитать угловое расстояние θ в угловых секундах для двойной звёздные системы, экзопланеты, объекта Солнечной системы и других астрономических объектов, используется размер большой полуоси, выраженной в астрономических единицах (а.е.), деленное на расстояние D, выраженное в парсеках, согласно формуле для малых углов — tan(aD){\displaystyle \tan({\frac {a}{D}})}:
- θ≈aD{\displaystyle \theta \approx {\dfrac {a}{D}}}
Учитывая два угловых положения, каждое из которых определяется прямым восхождением (RA), α∈[0,2π]{\displaystyle \alpha \in [0,2\pi ]} и склонением (dec), δ∈[−π/2,π/2]{\displaystyle \delta \in [-\pi /2,\pi /2]} угловое расстояние между двумя точками можно рассчитать, используя следующую формулу:
- θ=cos−1[sin(δ1)sin(δ2)+cos(δ1)cos(δ2)cos(α1−α2)]{\displaystyle \theta =\cos ^{-1}\left[\sin(\delta _{1})\sin(\delta _{2})+\cos(\delta _{1})\cos(\delta _{2})\cos(\alpha _{1}-\alpha _{2})\right]}
Как обозначается расстояние в физике? Интересные примеры
Тема посвящена тем учащимся, у кого физика только первый год. Здесь мы поговорим не только о том, как обозначается расстояние в физике, но и о других интересных вещах. Пусть этот предмет будет интересным по всем разделам и темам.
Какое же оно – расстояние?
В физике у каждой физической величины имеется свой символ (обозначение или на латинице, или греческой буквой). Все это сделано для того, чтобы было проще и не путаться. Согласитесь, можно замучиться при написании в тетрадь примерно такой фразы: расстояние = скорость х время. А в физике очень и очень много различных формул с множеством параметров. Причем встречаются и квадратные, и кубические величины. Так какой буквой обозначается расстояние в физике? Сразу оговоримся, что встречаются двух видов обозначения, так как расстояние и длина имеют одинаковые величины и одни и те же единицы измерения. Итак, «S» — это то самое обозначение. Встретите такую букву в задачках или формулах из раздела «Механика».
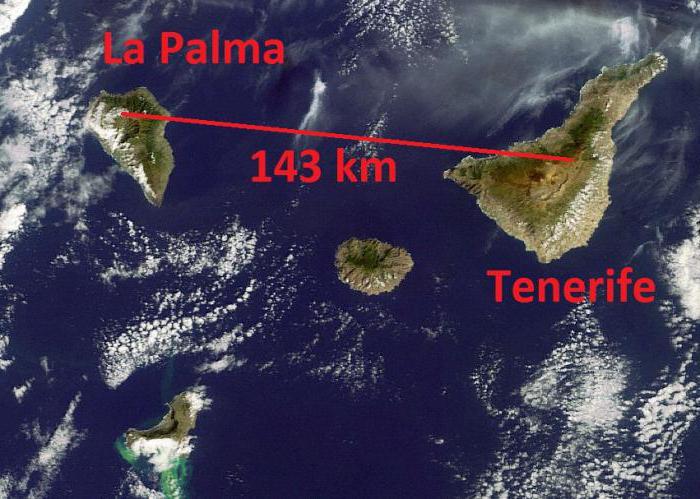
Поверьте, в решении задач нет ничего сложного. Но при условии, что вы знаете математику и успеваете по ней. Вам понадобятся знания по операциям с дробями, умение считать, раскрывать скобки, решать уравнения. Без таких навыков по физике будет очень сложно.
Примеры из жизни
Что же такое расстояние? Как обозначается расстояние в физике, мы уже уяснили. Теперь разберемся с понятием.
Представьте себе, что вы сейчас стоите возле своего дома. Ваша задача – дойти до школы. Дорога все время прямая. Идти от силы около двух минут. От дверей подъезда до школьных дверей 200 метров. Это и есть расстояние. Как будет выглядеть описание вашей прогулки от дома до школы?
S=200 м.
Почему мы не написали «метров», а ограничились только буквой? Потому что такое вот сокращенное буквенное обозначение. Чуть позже познакомимся и с другими параметрами, которые связаны с расстоянием.
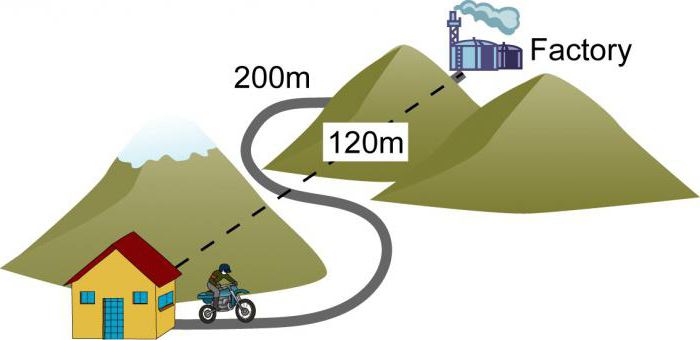
А теперь представьте, что путь от дома до магазина извилистый. Если посмотрите на карту своего района, то увидите, что до магазина от дома расстояние такое же, как до школы. Но почему же путь такой длинный? Потому что дорога не прямая. Приходится переходить у светофора, обходить огромный жилой дом и только уже вы попадаете в магазин. В таком случае фактическое расстояние будет намного больше. В геометрии и физике это обозначает «кривой путь». А прямая линия – это всего лишь чистое расстояние, будто идете сквозь стену большого дома. Можно еще привести пример и с мужчиной, который едет на работу.
С чем связано расстояние?
Понятие «расстояние» не может существовать само по себе, оно должно играть какую-то роль. Например, вы едете на велосипеде в школу, а не идете пешком, потому что опаздываете. Как мы говорили ранее, наш путь до школы прямой. Можно спокойно ехать по тротуару. Естественно, если перемещаться пешком, то получится дольше, чем проделать путь на велосипеде. В чем же здесь дело? Речь, разумеется, идет о скорости, с которой перемещаетесь. Позже мы увидим формулы, которые подскажут, как найти расстояние. Физика – это такая наука, в которой приходится что-то вычислять. Согласитесь, интересно же, с какой скоростью вы едете на велосипеде? Если вы знаете точно расстояние до школы и время перемещения, то найдете и скорость.
Итак, у нас появились еще два параметра:
t – время,
v – скорость.
Все будет намного интереснее, если научитесь работать с формулами и находить неизвестное с помощью дробей. Напомним лишь только правило из математики: все, что находится рядом с неизвестным, идет в знаменатель (то есть вниз дроби). Например, формула расстояния (физика) – это произведение времени и скорости. А в других случаях – дроби. Посмотрите на картинку, в которой изображено, как находить расстояние, скорость и время. Обязательно потренируйтесь и разберитесь, как получаются такие формулы. Все следует только из законов математики, ничего выдуманного в этих формулах нет. Давайте-ка потренируемся (не подглядывайте): какой буквой обозначается расстояние в физике?
В чем измеряются?
Будем надеяться, что вы запомнили обозначение основных величин, их обозначения. Пришла пора изучать единицы измерений. Здесь тоже придется тренировать память, запоминать. Важно знать, не только как обозначается расстояние в физике, но и время, скорость. А ведь это только маленькая тема. Дальше будет сложнее. Давайте приступим:
S – расстояние – метр, километр [м], [км];
v – скорость – метров в секунду, километров в час [м/с], [км/ч] (в случае космических скоростей может применяться километр в секунду;
t – время – секунда, минута, час [с], [мин],[ч].
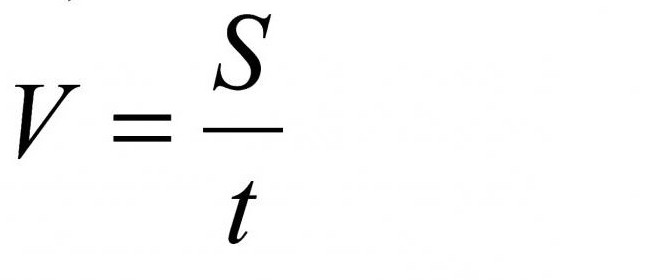
Обратите внимание, как обозначается скорость. Правильно, дробью. А теперь представьте вот что: S/t=м/с или S/t=км/ч. Вот откуда появились дроби. В системе международных единиц СИ эти параметры имеют величины метр, секунда, метр в секунду.
Мы разобрались, как обозначается расстояние в физике, рассмотрели время и скорость, которые неразрывно связаны с ним.
Отрезок — Википедия
Материал из Википедии — свободной энциклопедии
Эта статья — о понятии в геометрии и математическом анализе. О насильно отрезанных от крестьянских наделов землях см. Отрезки (земля).
Отрезок AB (выделен красным)Отре́зком называются два близких понятия: в геометрии и математическом анализе.
Отрезок прямой — часть прямой, ограниченная двумя точками. Точнее: это множество, состоящее из двух различных точек данной прямой (которые называются концами отрезка) и всех точек, лежащих между ними (которые называются его внутренними точками). Отрезок, концами которого являются точки A{\displaystyle \;A} и B{\displaystyle \;B}, обозначается символом AB{\displaystyle AB}. Расстояние между концами отрезка называют его длиной и обозначают AB{\displaystyle AB} или |AB|{\displaystyle |AB|}.
Направленный отрезок[править | править код]
Обычно у отрезка прямой неважно, в каком порядке рассматриваются его концы: то есть отрезки AB{\displaystyle AB} и BA{\displaystyle BA} представляют собой один и тот же отрезок. Если у отрезка определить направление, то есть порядок перечисления его концов, то такой отрезок называется направленным. Например, направленные отрезки AB{\displaystyle AB} и BA{\displaystyle BA} не совпадают. Отдельного обозначения для направленных отрезков нет — то, что у отрезка важно его направление, обычно указывается особо.
Дальнейшее обобщение приводит к понятию вектора — класса всех равных по длине и сонаправленных направленных отрезков.
Отрезок числовой (координатной) прямой (иначе числовой отрезок, сегмент) — множество вещественных чисел {x}{\displaystyle \{x\}}, удовлетворяющих неравенству a≤x≤b{\displaystyle a\leq x\leq b}, где заранее заданные вещественные числа a{\displaystyle a} и b{\displaystyle b} (a<b){\displaystyle (a<b)} называются концами (граничными точками) отрезка. В противоположность им, остальные числа x{\displaystyle x}, удовлетворяющие неравенству a<x<b{\displaystyle a<x<b}, называются внутренними точками отрезка[1].
Отрезок обычно обозначается [a,b]{\displaystyle [a,b]}:
- [a,b]={x∈R∣a≤x≤b}{\displaystyle [a,b]=\{x\in \mathbb {R} \mid a\leq x\leq b\}}.
Любой отрезок, по определению, заведомо включён в множество вещественных чисел. Отрезок является замкнутым промежутком.
Число b−a{\displaystyle b-a} называется длиной числового отрезка [a,b]{\displaystyle [a,b]}.
Стягивающаяся система сегментов[править | править код]
Система сегментов — это бесконечная последовательность элементов множества отрезков на числовой прямой {[a,b]|a,b∈R∧a<b}{\displaystyle \{[a,b]|a,b\in \mathbb {R} \land a<b\}}.
Система сегментов обозначается {[an,bn]}n=1∞{\displaystyle \{[a_{n},b_{n}]\}_{n=1}^{\infty }}. Подразумевается, что каждому натуральному числу n{\displaystyle n} поставлен в соответствие отрезок [an,bn]{\displaystyle [a_{n},b_{n}]}.
Система сегментов {[an,bn]}n=1∞{\displaystyle \{[a_{n},b_{n}]\}_{n=1}^{\infty }} называется стягивающейся, если[2]
- каждый следующий отрезок содержится в предыдущем;
- ∀n∈N:[an+1,bn+1]⊆[an,bn]{\displaystyle \forall n\in \mathbb {N} \colon [a_{n+1},b_{n+1}]\subseteq [a_{n},b_{n}]}
- соответствующая последовательность длин отрезков бесконечно мала.
- limn→∞(bn−an)=0{\displaystyle \lim _{n\to \infty }(b_{n}-a_{n})=0}
У любой стягивающейся системы сегментов существует единственная точка, принадлежащая всем сегментам этой системы.
- ∀{[an,bn]}n=1∞ ∃!c∈R ∀n∈N:c∈[an,bn]{\displaystyle \forall \{[a_{n},b_{n}]\}_{n=1}^{\infty }~\exists !c\in \mathbb {R} ~\forall n\in N\colon c\in [a_{n},b_{n}]}
Этот факт следует из свойств монотонной последовательности.
Промежуток (математика) — Википедия
Промежуток[1], или более точно, промежуток числовой прямой — множество вещественных чисел, обладающее тем свойством, что вместе с любыми двумя числами содержит любое, лежащее между ними[2]. С использованием логических символов, это определение можно записать так:
X⊂R{\displaystyle X\subset \mathbb {R} } — промежуток, если
- ∀x∀y∀z((x∈X)∧(z∈X)∧(x<y<z)⇒y∈X).{\displaystyle \forall x\forall y\forall z{\big (}(x\in X)\wedge (z\in X)\wedge (x<y<z)\Rightarrow y\in X{\big )}.}
В качестве примеров промежутков можно привести следующие множества:
- X1={x∈R:0⩽x⩽1},X2={x∈R:0⩽x<1},X3={x∈R:0<x⩽1},X4={x∈R:0<x<1},X5={x∈R:x>0},X6={x∈R:x<1},X7=R,X8=∅.{\displaystyle {\begin{aligned}X_{1}&=\{x\in \mathbb {R} \colon 0\leqslant x\leqslant 1\},&X_{2}&=\{x\in \mathbb {R} \colon 0\leqslant x<1\},&X_{3}&=\{x\in \mathbb {R} \colon 0<x\leqslant 1\},\\X_{4}&=\{x\in \mathbb {R} \colon 0<x<1\},&X_{5}&=\{x\in \mathbb {R} \colon x>0\},&X_{6}&=\{x\in \mathbb {R} \colon x<1\},\\X_{7}&=\mathbb {R} ,&X_{8}&=\varnothing .\end{aligned}}}
Конечный промежуток состоит из множества чисел, заключенных между двумя числами a{\displaystyle a} и b{\displaystyle b} — концами промежутка, которые сами могут быть включены в его состав, или нет[1].
Если a⩽b,a∈R,b∈R{\displaystyle a\leqslant b,a\in \mathbb {R} ,b\in \mathbb {R} }, то промежуток {x∈R:a⩽x⩽b}{\displaystyle \{x\in \mathbb {R} \colon a\leqslant x\leqslant b\}} называется сегментом[3] или числовым отрезком, и обозначается [a,b]{\displaystyle [a,b]}:
- [a,b] =def {x∈R:a⩽x⩽b}.{\displaystyle [a,b]\ {\stackrel {\text{def}}{=}}\ \{x\in \mathbb {R} \colon a\leqslant x\leqslant b\}.}
В случае a=b{\displaystyle a=b} отрезок состоит из одной точки.
Если a<b,a∈R,b∈R{\displaystyle a<b,a\in \mathbb {R} ,b\in \mathbb {R} }, то промежуток {x∈R:a<x<b}{\displaystyle \{x\in \mathbb {R} \colon a<x<b\}} называется интервалом и обозначается (a,b){\displaystyle (a,b)}:
- (a,b) =def {x∈R:a<x<b}.{\displaystyle (a,b)\ {\stackrel {\text{def}}{=}}\ \{x\in \mathbb {R} \colon a<x<b\}.}
В средней школе для обозначения открытого промежутка вместо (a,b){\displaystyle (a,b)} иногда используют обозначение ]a,b[{\displaystyle ]a,b[}.
Промежутки
- [a,b) =def {x∈R:a⩽x<b},(a,b] =def {x∈R:a<x⩽b}{\displaystyle [a,b)\ {\stackrel {\text{def}}{=}}\ \{x\in \mathbb {R} \colon a\leqslant x<b\},\quad (a,b]\ {\stackrel {\text{def}}{=}}\ \{x\in \mathbb {R} \colon a<x\leqslant b\}}
называются полусегментами (не дополненными до сегмента) или полуинтервалами.
Длиной промежутка во всех случаях называется число b−a{\displaystyle b-a}.
Бесконечные промежутки
- {x∈R:x⩾a},{x∈R:x>a},{x∈R:x⩽b},{x∈R:x<b},R{\displaystyle \{x\in \mathbb {R} \colon x\geqslant a\},\quad \{x\in \mathbb {R} \colon x>a\},\quad \{x\in \mathbb {R} \colon x\leqslant b\},\quad \{x\in \mathbb {R} \colon x<b\},\quad \mathbb {R} }
не ограничены либо сверху, либо снизу каким-либо вещественным числом. В этом случае удобно считать, что у этих промежутков одним из концов, или обоими служат несобственные числа +∞,−∞{\displaystyle +\infty ,-\infty }, полагая, что для любого вещественного числа x∈R{\displaystyle x\in \mathbb {R} } справедливы неравенства x<+∞,x>−∞{\displaystyle x<+\infty ,x>-\infty }. Обозначения и наименования бесконечных промежутков аналогичны таковым для конечных промежутков. Например, выписанные выше бесконечные промежутки обозначаются соответственно
- [a,+∞),(a,+∞),(−∞,b],(−∞,b),(−∞,+∞).{\displaystyle [a,+\infty ),\quad (a,+\infty ),\quad (-\infty ,b],\quad (-\infty ,b),\quad (-\infty ,+\infty ).}
Пустое множество ∅{\displaystyle \varnothing } также является промежутком.
Промежутки расширенной числовой прямой[править | править код]
Множество вещественных чисел R{\displaystyle \mathbb {R} }, дополненное элементами +∞{\displaystyle +\infty } и −∞{\displaystyle -\infty }, называется расширенной числовой прямой и обозначается R¯{\displaystyle {\overline {\mathbb {R} }}}, то есть
- R¯=R∪{+∞}∪{−∞}{\displaystyle {\overline {\mathbb {R} }}=\mathbb {R} \cup \{+\infty \}\cup \{-\infty \}}
При этом для любого вещественного числа x∈R{\displaystyle x\in \mathbb {R} } по определению полагают выполненными неравенства
- −∞<x,x<+∞,−∞<+∞{\displaystyle -\infty <x,\quad x<+\infty ,\quad -\infty <+\infty }
Для расширенной числовой прямой также вводят понятия промежутков — отрезков, интервалов, полуинтервалов[1]. В отличие от соответствующих промежутков числовой прямой они могут содержать элементы ±∞{\displaystyle \pm \infty }. Например, (a,+∞]=(a,+∞)∪{+∞}{\displaystyle (a,+\infty ]=(a,+\infty )\cup {\{+\infty \}}}.
В русском языке слова промежуток и интервал соответствуют одному английскому слову interval. В англоязычной литературе[4] и в переводах иностранных книг, а также в некоторых других книгах на русском языке используется следующая терминология:
- [a,b]={x∈R:a⩽x⩽b}{\displaystyle [a,b]=\{x\in \mathbb {R} \colon a\leqslant x\leqslant b\}} — замкнутый интервал (англ. closed interval),
- (a,b)={x∈R:a<x<b}{\displaystyle (a,b)=\{x\in \mathbb {R} \colon a<x<b\}} — открытый интервал (англ. open interval),
- [a,b)={x∈R:a⩽x<b}{\displaystyle [a,b)=\{x\in \mathbb {R} \colon a\leqslant x<b\}} — полуоткрытый (или полузамкнутый) интервал (англ. half-open interval/half-closed interval),
- (a,b]={x∈R:a<x⩽b}{\displaystyle (a,b]=\{x\in \mathbb {R} \colon a<x\leqslant b\}} — полуоткрытый (или полузамкнутый) интервал (англ. half-open interval/half-closed interval).
То есть, различные типы интервалов.
В более старой русскоязычной литературе[5] вместо «интервал» используется слово промежуток: замкнутый промежуток, открытый промежуток, полуоткрытый (или полузамкнутый) промежуток.
Однако, особенно в учебной литературе, где наибольшее количество теорем для функций на компактных множествах, для замкнутого промежутка предпочтительно иметь отдельное название в одно слово — сегмент[3] (термин «отрезок» имеет скорее геометрический оттенок, как и «промежуток числовой прямой»). В этом случае термин «интервал» закрепляется только за открытым промежутком.
См. также открытые и замкнутые множества.
Теорема о промежуточных значениях[править | править код]
Известная теорема Больцано — Коши о промежуточных значениях непрерывной функции гласит: образ любого промежутка при непрерывном отображении снова есть промежуток. Как следует из обобщения этой теоремы на случай произвольных топологических пространств, эта теорема — следствие того факта, что промежутки — в точности связные подмножества R{\displaystyle \mathbb {R} }. См. ниже связные множества.
Операции с промежутками[править | править код]
На практике промежуток нередко характеризует интервал возможных значений (приближённо) измеренной величины. На множестве таких промежутков можно определить арифметические операции. Тогда результату вычислений над величинами можно сопоставить соответствующие вычисления над их интервалами, задающие в итоге интервал возможных значений для результата.
Мера[править | править код]
Промежутки числовой прямой, прямоугольники на плоскости, прямоугольные параллелепипеды в пространстве и т. п. являются отправной точкой в теории меры, поскольку являются простейшими множествами, меру которых (длину, площадь, объем и т. п.) легко определить.
Связные множества[править | править код]
Обобщением промежутка числовой прямой является понятие связного топологического пространства. На числовой прямой всякое связное множество есть промежуток, и обратно, любой промежуток есть связное множество.
Также промежуток числовой прямой лежит в основе другого, более специального понятия линейной связности. Во множестве вещественных чисел R{\displaystyle \mathbb {R} }, а также в евклидовом пространстве Rn{\displaystyle \mathbb {R} ^{n}} произвольной размерности n{\displaystyle n} понятия связности и линейной связности совпадают.
Выпуклые множества[править | править код]
Другим обобщением понятия промежутка числовой прямой является понятие выпуклого множества.
Промежутки в частично упорядоченных множествах[править | править код]
В самом общем случае понятие промежутка можно ввести на любом множестве, на котором введено отношение порядка <{\displaystyle <}.
- ↑ 1 2 3 Кудрявцев, Л. Д. Курс математического анализа. — 5-е изд. — М.: «Дрофа», 2003. — Т. 1. — С. 64—65. — 704 с. — ISBN 5-7107-4119-1.
- ↑ В ряде источников описывается как интервал; например, см. Интервал // Казахстан. Национальная энциклопедия. — Алматы: Қазақ энциклопедиясы, 2005. — Т. II. — ISBN 9965-9746-3-2.
- ↑ 1 2 В. А. Ильин, В. А. Садовничий, Бл. Х. Сендов. Глава 2. Вещественные числа // Математический анализ / Под ред. А. Н. Тихонова. — 3-е изд., перераб. и доп. — М.: Проспект, 2006. — Т. I. — С. 53. — 672 с. — ISBN 5-482-00445-7.
- ↑ Гелбаум, Б., Олмстед, Дж. Контрпримеры в анализе = Counterexamples in Analysis. — М.: ЛКИ, 2007. — С. 17—18. — 258 с. — ISBN 978-5-382-00046-6.
- ↑ Фихтенгольц, Г. М. Основы математического анализа. — 7-е изд. — М.: «ФИЗМАТЛИТ», 2002. — Т. 1. — С. 35. — 416 с. — ISBN 5-9221-0196-X.
Окружность, круг, сегмент, сектор. Формулы и свойства
Определение. Окружность — это совокупность всех точек на плоскости, которые находятся на одинаковом расстоянии от заданной точки О, которая называется центром окружности.
Определение. Единичная окружность — окружность, радиус которой равна единице.
Определение. Круг — часть плоскости, ограничена окружностью.
Определение. Радиус окружности R — расстояние от центра окружности О до любой точки окружности.
Определение. Диаметр окружности D — отрезок, который соединяет две точки окружности и проходит через ее центр.
Основные свойства окружности
1. Диаметр окружности равен двум радиусам.D = 2r
2. Кратчайшее расстояние от центра окружности к секущей (хорде) всегда меньше радиуса.
3. Через три точки, которые не лежат на одной прямым, можно провести только одну окружность.
4. Среди всех замкнутых кривых с одинаковой длиной, окружность имеет наибольшую площадь.
5. Если две окружности соприкасаются в одной точке, то эта точка лежит на прямой, что проходит через центры этих окружностей.
Формулы длины окружности и площади круга
Формулы длины окружности
1. Формула длины окружности через диаметр:L = πD
2. Формула длины окружности через радиус:L = 2πr
Формулы площади круга
1. Формула площади круга через радиус:S = πr2
2. Формула площади круга через диаметр:S = πD24
Уравнение окружности
1. Уравнение окружности с радиусом r и центром в начале декартовой системы координат:r2 = x2 + y2
2. Уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:r2 = (x — a)2 + (y — b)2
3. Параметрическое уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:| { | x = a + r cos t |
| y = b + r sin t |
Касательная окружности и ее свойства
Определение. Касательная окружности — прямая, которая касается окружности только в одной точке.
Основные свойства касательных к окружности
1. Касательная всегда перпендикулярна к радиусу окружности, проведенного в точке соприкосновения.
2. Кратчайшее расстояние от центра окружности к касательной равна радиусу окружности.
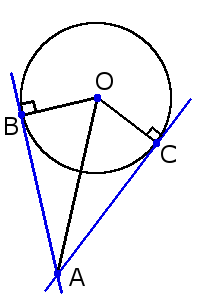3. Если две касательные, с точками соприкосновения B и C, на одной окружности не параллельны, то они пересекаются в точке A, а отрезок между точкой соприкосновения и точкой пересечения одной касательной равен таком же отрезке на другой касательной:AB = AC
Также, если провести прямую через центр окружности О и точку пересечения A этих касательных, то углы образованный между этой прямой и касательными будут равны:∠ОAС = ∠OAB
Секущая окружности и ее свойства
Определение. Секущая окружности — прямая, которая проходит через две точки окружности.
Основные свойства секущих
1. Если с точки вне окружности (Q) выходят две секущие, которые пересекают окружность в двух точках A и B для одной секущей и C и D для другой секущей, то произведения отрезков двух секущих равны между собою:AQ ∙ BQ = CQ ∙ DQ
2. Если из точки Q вне окружности выходит секущая прямая, что пересекает окружность в двух точках A и B, и касательная с точкой соприкосновения C, то произведение отрезков секущей равна квадрату длины отрезка касательной:AQ ∙ BQ = CQ2
Хорда окружности ее длина и свойства
Определение. Хорда окружности — отрезок, который соединяет две точки окружности.
Длина хорды
1. Длина хорды через центральный угол и радиус:AB = 2r sin α2
2. Длина хорды через вписанный угол и радиус:AB = 2r sin α
Основные свойства хорд
1. Две одинаковые хорды стягивают две одинаковые дуги:если хорды AB = CD, то
дуги ◡ AB = ◡ CD
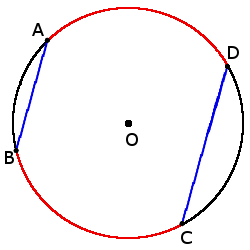2. Если хорды параллельные, то дуги между ними будут одинаковые:если хорды AB ∣∣ CD, то
◡ AD = ◡ BC
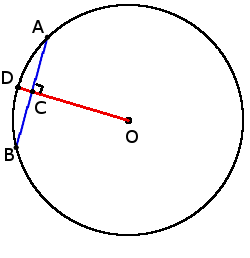3. Если радиус окружности перпендикулярен к хорде, то он разделяет хорду пополам в точке их пересечения:если OD ┴ AB, то
AC = BC
4. Если две хорды AB и CD пересекаются в точке Q, то произведение отрезков, что образовались при пересечении, одной хорды равны произведению отрезков другой хорды:AQ ∙ BQ = DQ ∙ QC
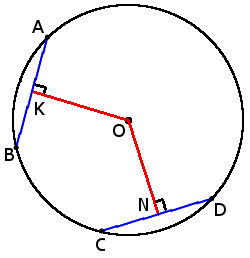5. Хорды с одинаковой длиной находятся на одинаковом расстоянии от центра окружности.если хорды AB = CD, то
ON = OK
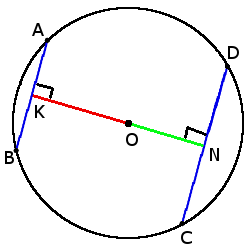6. Чем больше хорда тем ближе она к центру.если CD > AB, то
ON < OK
Центральный угол, вписанный угол и их свойства
Определение. Центральный угол окружности — угол, вершиной которого есть центр окружности.
Определение. Угол вписанный в окружность — угол, вершина которого лежит на окружности, а стороны угла пересекают окружность.
Основные свойства углов
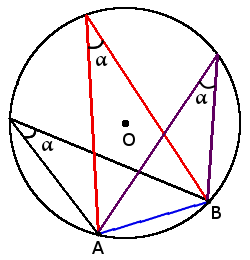1. Все вписанные углы, которые опираются на одну дугу — равны. 
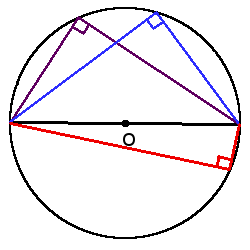2. Вписанний угол, который опирается на диаметр будет прямым (90°). 
3. Вписанный угол равен половине центрального угла, что опирается на ту же дугуβ = α2
4. Если два вписанных угла опираются на одну хорду и находятся по различные стороны от нее, то сумма этих углов равна 180°.α + β = 180°
Определение. Дуга окружности (◡) — часть окружности, которая соединяет две точки на окружности.
Определение. Градусная мера дуги — угол между двумя радиусами, которые ограничивают эту дугу. Градусная мера дуги всегда равна градусной мере центрального угла, который ограничивает эту дугу своими сторонами.
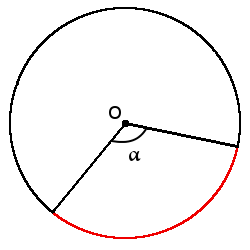Формула длины дуги через центральный угол (в градусах):l = πr180°∙ α
Определение. Полуокружность — дуга в которой концы соединены диаметром окружности.
Определение. Полукруг (◓) — часть круга, которая ограничена полуокружностью и диаметром.
Определение. Сектор (◔) — часть круга, которая ограничена двумя радиусами и дугой между этими радиусами.
Формула. Формула площади сектор через центральный угол (в градусах)S = πr2360°∙ α
Определение. Сегмент — часть круга, которая ограничена дугой и хордой, что соединяет ее концы.
Определение. Концентрические окружности — окружности с различными радиусами, которые имеют общий центр.
Определение. Кольцо — часть плоскости ограниченная двумя концентрическими окружностями.