Расчет балки на изгиб формула – Расчет балки на прогиб ℹ️ построение эпюр, формулы, параметры расчетов, определение максимальной нагрузки и изгиба, примеры решения задач, онлайн-калькулятор

Формулы для расчетов на изгиб

σ — нормальные напряжения,
τ — касательные напряжения,
Q_y – внутренняя поперечная сила,
M_x – внутренний изгибающий момент,
I_x – осевой момент инерции сечения балки,
W_x – осевой момент сопротивления сечения,
[σ], [τ] – соответствующие допустимые напряжения,
E – модуль упругости I рода (модуль Юнга),
y — расстояние от оси x до рассматриваемой точки сечения балки.

Расчет внутренних поперечных сил и изгибающих моментов

Формула кривизны балки в заданном сечении

Расчет нормальных напряжений в произвольной точке сечения балки

Условие прочности по нормальным напряжениям при изгибе (проверочный расчет)

Осевые моменты инерции I и сопротивления W

• прямоугольного сечения
  
  h – высота сечения,
  b – ширина сечения балки.
• круглого сечения балки
  
  D — диаметр сечения

Касательные напряжения в произвольной точке сечения определяются по формуле Журавского:

Здесь:

S_x^* — статический момент относительно оси x отсеченной части сечения

b — ширина сечения на уровне рассматриваемой точки

Условие прочности балки по касательным напряжениям

Дифференциальное уравнение линии изогнутой оси балки

Уравнения метода начальных параметров (МНП)

θ_z, y_z — соответственно угол наклона и прогиб сечения балки на расстоянии z от начала координат,
θ₀, y₀ — соответственно угол наклона и прогиб сечения балки в начале координат,
m, F, q — соответственно все изгибающие моменты, сосредоточенные силы и распределенные нагрузки приложенные к балке,

a, b — расстояние от начала координат до сечений где приложены моменты и силы соответственно,
c — расстояние от начала координат до начала распределенной нагрузки q.

Другие формулы >
Примеры решения задач >
Краткая теория >

Расчет балки на изгиб | Блог Александра Воробьева

Опубликовано 28 Апр 2013
Рубрика: Механика | 88 комментариев

Расчет балки на изгиб «вручную», по-дедовски, позволяет познать один из важнейших, красивейших, четко математически выверенных алгоритмов науки сопротивление материалов. Использование многочисленных программ типа «ввел исходные данные…

…– получи ответ» позволяет современному инженеру сегодня работать гораздо быстрее, чем его предшественникам сто, пятьдесят и даже двадцать лет назад. Однако при таком современном подходе инженер вынужден полностью доверять авторам программы и со временем перестает «ощущать физический смысл» расчетов. Но авторы программы – это люди, а людям свойственно ошибаться. Если бы это было не так, то не было бы многочисленных патчей, релизов, «заплаток» практически к любому программному обеспечению. Поэтому, мне кажется, любой инженер должен уметь иногда «вручную» проверить результаты расчетов.

Справка (шпаргалка, памятка) для расчётов балок на изгиб представлена ниже на рисунке.

Давайте на простом житейском примере попробуем ей воспользоваться. Допустим, я решил сделать в квартире турник. Определено место – коридор шириной один метр двадцать сантиметров. На противоположных стенах на необходимой высоте напротив друг друга надежно закрепляю кронштейны, к которым будет крепиться балка-перекладина – пруток из стали Ст3 с наружным диаметром тридцать два миллиметра. Выдержит  ли эта балка мой вес плюс дополнительные динамические нагрузки, которые возникнут при выполнении упражнений?

Чертим схему для расчета балки на изгиб. Очевидно, что наиболее опасной будет схема приложения внешней нагрузки, когда я начну подтягиваться, зацепившись одной рукой за середину перекладины.

Исходные данные:

F1 = 900 н – сила, действующая на балку (мой вес) без учета динамики

b1 = 0 м

b2 = 0,6 м

b3 = 1,2 м

d = 32 мм – наружный диаметр прутка, из которого сделана балка

E = 206000 н/мм^2 — модуль упругости материала балки стали Ст3

[σи] = 250 н/мм^2 — допустимые напряжения изгиба (предел текучести) для материала балки   стали Ст3

Граничные условия:

Мx (0) = 0 н*м – момент в точке z = 0 м (первая опора)

Мx (1,2) = 0 н*м– момент в точке z = 1,2 м (вторая опора)

V (0) = 0 мм – прогиб в точке z = 0 м (первая опора)

V (1,2) = 0 мм – прогиб в точке z = 1,2 м (вторая опора)

Расчет:

1. Для начала вычислим момент инерции Ix и момент сопротивления Wx сечения балки. Они нам пригодятся в дальнейших расчетах. Для кругового сечения (каковым является сечение прутка):

Ix = (π*d^4)/64 = (3.14*(32/10)^4)/64 = 5,147 см^4

Wx = (π*d^3)/32 = ((3.14*(32/10)^3)/32) = 3,217 см^3

2. Составляем уравнения равновесия для вычисления реакций опор R1 и R2:

Qy = -R1+F1-R2 = 0

Мx (0) = F1*(0-b2) -R2*(0-b3) = 0

Из второго уравнения: R2 = F1*b2/b3 = 900*0.6/1.2 = 450 н

Из первого уравнения: R1 = F1-R2 = 900-450 = 450 н

3. Найдем угол поворота балки в первой опоре при z = 0 из уравнения прогиба для второго участка:

V (1.2) = V (0)+U (0)*1.2+(-R1*((1.2-b1)^3)/6+F1*((1.2-b2)^3)/6)/

/(E*Ix) = 0

U (0) = (R1*((1.2-b1)^3)/6 -F1*((1.2-b2)^3)/6)/(E*Ix)/1,2 =

= (450*((1.2-0)^3)/6 -900*((1.2-0.6)^3)/6)/

/(206000*5,147/100)/1,2  = 0,00764 рад = 0,44˚

4. Составляем уравнения для построения эпюр для первого участка (0<z<b2):

Поперечная сила: Qy (z) = -R1

Изгибающий момент: Мx (z) = -R1*(z-b1)

Угол поворота: Ux (z) = U (0)+(-R1*((z-b1)^2)/2)/(E*Ix)

Прогиб: Vy (z) = V (0)+U (0)*z+(-R1*((z-b1)^3)/6)/(E*Ix)

z = 0 м:

Qy (0) = -R1 = -450 н

Мx (0) = 0

Ux (0) = U (0) = 0,00764 рад

Vy (0) = V (0) = 0 мм

z = 0,6 м:

Qy (0,6) = -R1 = -450 н

Мx (0,6) = -R1*(0,6-b1) = -450*(0,6-0) = -270 н*м

Ux (0,6) = U (0)+(-R1*((0,6-b1)^2)/2)/(E*Ix) =

= 0,00764+(-450*((0,6-0)^2)/2)/(206000*5,147/100) = 0 рад

Vy (0,6) = V (0)+U (0)*0,6+(-R1*((0,6-b1)^3)/6)/(E*Ix) =

= 0+0,00764*0,6+(-450*((0,6-0)^3)/6)/ (206000*5,147/100) = 0,003 м

Балка прогнется по центру на 3 мм под тяжестью моего тела. Думаю, это приемлемый прогиб.

5. Пишем уравнения эпюр для второго участка (b2<z<b3):

Поперечная сила: Qy (z) = -R1+F1

Изгибающий момент: Мx (z) = -R1*(z-b1)+F1*(z-b2)

Угол поворота: Ux (z) = U (0)+(-R1*((z-b1)^2)/2+F1*((z-b2)^2)/2)/(E*Ix)

Прогиб: Vy (z) = V (0)+U (0)*z+(-R1*((z-b1)^3)/6+F1*((z-b2)^3)/6)/(E*Ix)

z = 1,2 м:

Qy (1,2) = -R1+F1 = -450+900 = 450 н

Мx (1,2) = 0 н*м

Ux (1,2) = U (0)+(-R1*((1,2-b1)^2)/2+F1*((1,2-b2)^2)/2)/(E*Ix) =

= 0,00764+(-450*((1,2-0)^2)/2+900*((1,2-0,6)^2)/2)/

/(206000*5,147/100) = -0.00764 рад

Vy (1,2) = V (1,2) = 0 м

6. Строим эпюры, используя данные полученные выше.

7. Рассчитываем напряжения изгиба в наиболее нагруженном сечении – посередине балки и сравниваем с допустимыми напряжениями:

σи = Mx max/Wx = (270*1000)/(3,217*1000) = 84 н/мм^2

σи = 84 н/мм^2 < [σи] = 250 н/мм^2

По прочности на изгиб расчет показал трехкратный запас прочности – турник можно смело делать из имеющегося прутка диаметром тридцать два миллиметра и длиной тысяча двести миллиметров.

Таким образом, вы теперь легко можете произвести расчет балки на изгиб «вручную» и сравнить с результатами, полученными при расчете по любой из многочисленных программ, представленных в Сети.

Прошу УВАЖАЮЩИХ труд автора ПОДПИСАТЬСЯ на анонсы статей.

Другие статьи автора блога

На главную

Статьи с близкой тематикой

Отзывы

Расчет балки на изгиб — favorit-tk

Расчет балки на изгиб
Рассчитывать балку на изгиб можно несколькими вариантами:
1. Расчет максимальной нагрузки, которую она выдержит
2. Подбор сечения этой балки
3. Расчет по максимальным допустимым напряжениям (для проверки)[/i]
Давайте рассмотрим общий принцип подбора сечения балки на двух опорах загруженной равномерно распределенной нагрузкой или сосредоточенной силой.
Для начала, вам необходимо будет найти точку (сечение), в которой будет максимальный момент. Это зависит от опирания балки или же ее заделки. Снизу приведены эпюры изгибающих моментов для схем, которые встречаются чаще всего.
После нахождения изгибающего момента мы должны найти момент сопротивления Wx этого сечения по формуле приведенной в таблице:
Далее, при делении максимального изгибающего момента на момент сопротивления в данном сечении, мы получаем максимальное напряжение в балке и это напряжение мы должны сравнить с напряжением, которое вообще сможет выдержать наша балка из заданного материала.
Для пластичных материалов (сталь, алюминий и т.п.) максимальное напряжение будет равно пределу текучести материала, а для хрупких (чугун) – пределу прочности. Предел текучести и предел прочности мы можем найти по таблицам ниже.
Давайте рассмотрим пару примеров:
1. [i]Вы хотите проверить, выдержит ли вас двутавр №10 (сталь Ст3сп5) длиной 2 метра жестко заделанного в стену, если вы на нем повисните. Ваша масса пусть будет 90 кг.[/i]
Для начала нам необходимо выбрать расчетную схему.
На данной схеме видно, что максимальный момент будет в заделке, а поскольку наш двутавр имеет одинаковое сечение по всей длине, то и максимальное напряжение будет в заделке. Давайте найдем его:
P = m * g = 90 * 10 = 900 Н = 0.9 кН
М = P * l = 0.9 кН * 2 м = 1.8 кН*м
По таблице сортамента двутавров находим момент сопротивления двутавра №10.
Он будет равен 39.7 см3. Переведем в кубические метры и получим 0.0000397 м3.
Далее по формуле находим максимальные напряжения, которые у нас возникают в балке.
б = М / W = 1.8 кН/м / 0.0000397 м3 = 45340 кН/м2 = 45.34 МПа
После того, как мы нашли максимальное напряжение, которое возникает в балке, то мы его может сравнить с максимально допустимым напряжением равным пределу текучести стали Ст3сп5 – 245 МПа.
45.34 МПа
2. [i]Поскольку у нас получился доволи-таки большой запас, то решим вторую задачу, в которой найдем максимально возможную массу, которую выдержит все тот же двутавр №10 длиной 2 метра.[/i]
Если мы хотим найти максимальную массу, то значения предела текучести и напряжения, которое будет возникать в балке, мы должны приравнять (б=245 Мпа = 245 000 кН*м2).
Далее по формуле б = М / W, находим максимальный момент.
М = б * W = 245 000 * 0.0000397 = 9.73 кН * м
Тогда по формуле M = P * L найдем P:
P = 9,73 кН/м / 2м = 4,87 кН = 487 кг
Итак, максимальная масса, которую выдержит двутавр №10 – 487 кг. Число это грубое, поскольку для простоты расчета мы не учитывали различные коэффициенты запаса, поэтому, чтобы подстраховаться, возьмите некий двукратный запас по прочности.

Расчет прогиба балки на двух опорах

Процесс проектирования современных строений и построек регулируется огромным количеством различных строительных норм и правил. В большинстве случаев нормы требуют обеспечения определенных характеристик, например, деформации или прогиба балок плит перекрытия под статической или динамической нагрузкой. Например, СНиП № 2.09.03-85 определяет для опор и эстакад прогиб балки не более чем в 1/150 длины пролета. Для чердачных перекрытий этот показатель составляет уже 1/200, а для межэтажных балок и того меньше – 1/250. Поэтому одним из обязательных этапов проектирования является выполнение расчета балки на прогиб.

Способы выполнить расчет и проверку на прогиб

Причина, по которой СНиПы устанавливают столь драконовские ограничения, проста и очевидна. Чем меньше деформация, тем больше запас прочности и гибкости конструкции. Для прогиба менее 0,5% несущий элемент, балка или плита все еще сохраняет упругие свойства, что гарантирует нормальное перераспределение усилий и сохранение целостности всей конструкции. С увеличением прогиба каркас здания прогибается, сопротивляется, но стоит, с выходом за пределы допустимой величины происходит разрыв связей, и конструкция лавинообразно теряет жесткость и несущую способность.

Просчитать прогиб конструкции можно несколькими способами:

• Воспользоваться программным онлайн-калькулятором, в котором «зашиты» стандартные условия, и не более того;
• Использовать готовые справочные данные для различных типов и видов балок, для различных опор схем нагрузок. Нужно только правильно идентифицировать тип и размер балки и определить искомый прогиб;
• Посчитать допустимый прогиб руками и своей головой, большинство проектировщиков так и делают, в то время как контролирующие архитектурные и строительные инспекции предпочитают второй способ расчета.

Измерив, насколько просела балка потолочного перекрытия, можно с 99% уверенностью определить, находится ли конструкция в аварийном состоянии или нет.

Методика выполнения расчета на прогиб

Прежде чем приступать к расчету, нужно будет вспомнить некоторые зависимости из теории сопротивления материалов и составить расчетную схему. В зависимости от того, насколько правильно выполнена схема и учтены условия нагружения, будет зависеть точность и правильность расчета.

Используем простейшую модель нагруженной балки, изображенной на схеме. Простейшей аналогией балки может быть деревянная линейка, фото.

В нашем случае балка:

1. Имеет прямоугольное сечение S=b*h, длина опирающейся части составляет L;
2. Линейка нагружена силой Q, проходящей через центр тяжести изгибаемой плоскости, в результате чего концы поворачиваются на небольшой угол θ, с прогибом относительно начального горизонтального положения, равным f;
3. Концы балки опираются шарнирно и свободно на неподвижных опорах, соответственно, не возникает горизонтальной составляющей реакции, и концы линейки могут перемещаться в произвольном направлении.

Для определения деформации тела под нагрузкой используют формулу модуля упругости, который определяется по соотношению Е=R/Δ, где Е – справочная величина, R— усилие, Δ— величина деформации тела.

Вычисляем моменты инерции и сил

Для нашего случая зависимость будет выглядеть так: Δ = Q/(S·Е). Для распределенной вдоль балки нагрузки q формула будет выглядеть так: Δ = q·h/(S·Е).

Далее следует наиболее принципиальный момент. Приведенная схема Юнга показывает прогиб балки или деформацию линейки так, если бы ее раздавливали под мощным прессом. В нашем случае балку изгибают, а значит, на концах линейки, относительно центра тяжести, приложены два изгибающих момента с разным знаком. Эпюра нагружения такой балки приведена ниже.

Чтобы преобразовать зависимость Юнга для изгибающего момента, необходимо обе части равенства умножить на плечо L. Получаем Δ*L = Q·L/(b·h·Е).

Если представить, что одна из опор жестко закреплена, а на второй будет приложен эквивалентный уравновешивающий момент сил M_max = q*L*2/8, соответственно, величина деформации балки будет выражаться зависимостью Δх = M·х/((h/3)·b·(h/2)·Е). Величину b·h²/6 называют моментом инерции и обозначают W. В итоге получается Δх = M·х/(W·Е) основополагающая формула расчета балки на изгиб W=M/E через момент инерции и изгибающий момент.

Чтобы точно выполнить расчет прогиба, потребуется знать изгибающий момент и момент инерции. Величину первого можно посчитать, но конкретная формула для расчета балки на прогиб будет зависеть от условий контакта с опорами, на которых находится балка, и способа нагружения, соответственно для распределенной или концентрированной нагрузки. Изгибающий момент от распределенной нагрузки считается по формуле Mmax = q*L²/8. Приведенные формулы справедливы только для распределенной нагрузки. Для случая, когда давление на балку сконцентрировано в определенной точке и зачастую не совпадает с осью симметрии, формулу для расчета прогиба приходится выводить с помощью интегрального исчисления.

Момент инерции можно представить, как эквивалент сопротивления балки изгибающей нагрузке. Величину момента инерции для простой прямоугольной балки можно посчитать по несложной формуле W=b*h³/12, где b и h – размеры сечения балки.

Из формулы видно, что одна и та же линейка или доска прямоугольного сечения может иметь совершенно разный момент инерции и величину прогиба, если положить ее на опоры традиционным способом или поставить на ребро. Недаром практически все элементы стропильной системы крыши изготавливаются не из бруса 100х150, а из доски 50х150.

Реальные сечения строительных конструкций могут иметь самые разные профили, от квадрата, круга до сложных двутавровых или швеллерных форм. При этом определение момента инерции и величины прогиба вручную, «на бумажке», для таких случаев становится нетривиальной задачей для непрофессионального строителя.

Формулы для практического использования

На практике чаще всего стоит обратная задача – определить запас прочности перекрытий или стен для конкретного случая по известной величине прогиба. В строительном деле очень сложно дать оценку запасу прочности иными, неразрушающими методами. Нередко по величине прогиба требуется выполнить расчет, оценить запас прочности здания и общее состояние несущих конструкций. Мало того, по выполненным измерениям определяют, является деформация допустимой, согласно расчету, или здание находится в аварийном состоянии.

Совет! В вопросе расчета предельного состояния балки по величине прогиба неоценимую услугу оказывают требования СНиПа. Устанавливая предел прогиба в относительной величине, например, 1/250, строительные нормы существенно облегчают определение аварийного состояния балки или плиты.

Например, если вы намерены покупать готовое здание, простоявшее достаточно долго на проблемном грунте, нелишним будет проверить состояние перекрытия по имеющемуся прогибу. Зная предельно допустимую норму прогиба и длину балки, можно безо всякого расчета оценить, насколько критическим является состояние строения.

Строительная инспекция при оценке прогиба и оценке несущей способности перекрытия идет более сложным путем:

• Первоначально измеряется геометрия плиты или балки, фиксируется величина прогиба;
• По измеренным параметрам определяется сортамент балки, далее по справочнику выбирается формула момента инерции;
• По прогибу и моменту инерции определяют момент силы, после чего, зная материал, можно выполнить расчет реальных напряжений в металлической, бетонной или деревянной балке.

Вопрос – почему так сложно, если прогиб можно получить, используя для расчета формулу для простой балки на шарнирных опорах f=5/24*R*L²/(E*h) под распределенным усилием. Достаточно знать длину пролета L, высоту профиля, расчетное сопротивление R и модуль упругости Е для конкретного материала перекрытия.

Ответ  прост — необходимо непросто рассчитать, но и сохранить на бумаге ход выполнения проверочного расчета, чтобы сделанные выводы о состоянии перекрытия можно было проверить и перепроверить по всем этапам проверки.

Совет! Используйте в своих расчетах существующие ведомственные сборники различных проектных организаций, в которых в сжатом виде сведены все необходимые формулы для определения и расчета предельного нагруженного состояния.

Заключение

Аналогичным образом поступает большинство разработчиков и проектантов серьезных построек. Программа – это хорошо, она помогает очень быстро выполнить расчет прогиба и основных параметров нагружения перекрытия, но важно также предоставить заказчику документальное подтверждение полученных результатов в виде конкретных последовательных расчетов на бумаге.

Что еще почитать по теме?

Автор статьи:

Сергей Новожилов — эксперт по кровельным материалам с 9-летним опытом практической работы в области инженерных решений в строительстве.

Понравилась статья? Поделись с друзьями в социальных сетях:

Facebook

Twitter

Вконтакте

Одноклассники

Google+

Расчёт балок на прочность при изгибе

Задача 1

В некотором сечении балки прямоугольного сечения 20×30см М=28 кНм, Q=19 кН.

Требуется:

а) определить нормальное и касательное напряжения в заданной точке К, отстоящей от нейтральной оси на расстоянии 11 см,

б) проверить прочность деревянной балки, если [σ]=10 МПа, [τ]=3 МПа.

Решение

а) Для определения σ_(К), τ_(К) и _maxσ,_maxτ потребуется знать величины осевого момента инерции всего сечения I_Н.О., осевого момента сопротивления W_Н.О., статического момента отсечённой части  и статического момента половины сечения S_max:

Тогда:

б) Проверка прочности:

— по условию прочности нормальных напряжений:

— по условию прочности касательных напряжений:

Задача 2

В некотором сечении балки М=10кНм, Q=40кН. Поперечное сечение – треугольное. Найти нормальное и касательное напряжения в точке, отстоящей от нейтральной оси на расстоянии 15 см.

где 

Тогда

где:

Тогда

Задача 3

Подобрать сечение деревянной балки в двух вариантах: круглое и прямоугольное (при

h/b=2), если [σ]=10 МПа, [τ]=3 МПа, и сравнить их по расходу материала.

Задаёмся направлениями опорных реакций А и В и составляем уравнения статики:

(1)          ∑М(В) = F·8 – М – А·6 + (q·6)·3 =0,

откуда 

(2)          ∑

М(А) = F·2 – М + В·6 — (q·6)·3 =0,

откуда 

Iучасток   

∑М(С) = М(z₁) +F·z₁=0,

ММ(z₁) = —F·z₁= — 30 ·z₁ —

– уравнение прямой.

При z₁ = 0:      М = 0,

z₁ = 2:      М =- 60 кНм.

∑у= — F — Q(z₁) = 0,

Q(z₁) = — F = -30 кН – постоянная функция.

II участок     

откуда

— уравнение параболы.

При z₂=0:     М = 0,

z₂=3м:  М = 30 · 3 – 5 · 3² = 90 — 45 = 45кНм,

z₂=6м:  М = 30 · 6 – 5 · 6² = 180 — 180 = 0.

∑у= Q(z₂) — q·z₂ + B= 0,

Q(z₂) = q·z₂ — B= 10·z₂ – 30 – уравнение прямой,

при  z₂ = 0:     Q = -30,

        z₂

= 6м:     Q = 10·6 – 30 = 30.

Определение аналитического максимума изгибающего момента второго участка:

из условиянаходим :

И тогда

Заметим, что скачок в эп.М расположен там, где приложен сосредоточенный момент М = 60кНм и равен этому моменту, а скачок в эп.Q – под сосредоточенной силой А = 60 кН.

Подбор сечения балок производится из условия прочности по нормальным напряжениям, куда следует подставлять наибольший по абсолютной величине изгибающий момент из эпюры М.

В данном случае максимальный момент по модулю М = 60кНм

откуда: :

а) сечение круглой формы d=?

б) сечение прямоугольной формы при h/b = 2:

тогда

Размеры сечения, определенные из условия прочности по нормальным напряжениям, должны удовлетворять также условию прочности по касательным напряжениям:

Для простых форм сечений известны компактные выражения наибольшего касательного напряжения:

— для круглого сечения 

— для прямоугольного сечения 

Воспользуемся этими формулами. Тогда

— для балки круглого сечения при :

— для балки прямоугольного сечения

Чтобы выяснить, какое сечение требует меньшего расхода материала, достаточно сравнить величины площадей поперечных сечений:

А_{прямоугольного} = 865,3см² < А_{круглого} = 1218,6см², следовательно, балка прямоугольного сечения в этом смысле выгоднее, чем круглого.

 

Задача 4

Подобрать двутавровое сечение стальной балки, если [σ]=160МПа, [τ]=80МПа. 

Задаёмся направлениями опорных реакций А и В и составляем два уравнения статики для их определения:

(1)              ∑М(А) = – М₁– F  ·2 — (q·8)·4 + М₂ + В·6 =0,

откуда 

(2)      ∑М(В) = – М₁– А · 6 + F · 4 + (q·8)·2 + М₂ =0,

откуда 

Проверка:

∑у = А – F – q · 8 + В = 104 – 80 – 20 · 8 +136 = 240 – 240 ≡ 0.

∑М(С) = М(z₁) — М₁=0,

М(z₁) = М₁= 40 кНм – постоянная функция.   

∑у= — Q(z₁) = 0,

Q(z₁) = 0.

II участок 

— парабола.

Приz₂=0:       М = 40 кНм,

z₂=1м:    М = 40 + 104 – 10=134кНм,

z₂=2м:    М = 40+ 104 · 2 – 10 · 2² = 208 кНм.

∑у=А — q·z₂ — Q(z₂) = 0,

Q(z₂) =А— q·z₂ = 104 –  20·z₂  – уравнение прямой,

при  z₂ = 0:       Q = 104кН,

        z₂ = 6м:    Q = 104 – 40 = 64кН.

III участок

— парабола.

Приz₃=0:       М = 24+40=-16 кНм,

z₃=2м:    М = 24 + 136·2 — 10 (2+2)² = 24 + 272 – 160 = 136кНм,

z₃=4м:    М = 24 + 136·4 – 10 (2+4)² = 24 + 544 – 360 = 208 кНм.

∑у=В — q(2+z₃ ) + Q(z₃) = 0,

Q(z₃) =- В + q(2+z₃ ) = -136 + 20 (2+z₃ )   – уравнение прямой,

при  z₃ = 0:        Q = -136 + 40 = — 94кН,

        z₃ = 4м:     Q = — 136 + 20 (2+4) = — 136 + 120 = — 16кН.

IV участок

— парабола.

z₄=0:       М = 0кНм,

z₄=1м:    М = – 10кНм,

z₄=2м:    М = — 40кНм.

∑у=- q·z₄ + Q(z₄) = 0,

Q(z₄) =q·z₄ = 20·z₄  – уравнение прямой.

Приz₄ = 0:       Q = 0,

        z₄ = 2м:     Q = 40кН.

Проверяем скачки в эпюрах:

а) В эпюре М скачок на правой опоре величиной 24кНм (от 16 до 40) равен сосредоточенному моменту М₂=24, приложенному в этом месте.

б) В эпюре Q три скачка:

первый из них на левой опоре соответствует сосредоточенной реакции А=104кН,

второй – под силой F=80кН и равен ей (64+16=80кН),

третий – на правой опоре и соответствует правой опорной реакции 136кН (94+40=136 кН)

Наконец, проектируем двутавровое сечение.

Подбор его размеров производится из условия прочности по нормальным напряжениям :

 

В сортаменте двутавровых профилей профиля с точно таким моментом сопротивления W_х нет. Есть № 40^а с W_х=1190 см³ и № 45^а с W_х=1430 см³

Попробуем  меньший из них. Если принять двутавр № 40^а, у которого W_х=1190 см³ , то наибольшее напряжение в опасном сечении будет:

и перенапряжение составитчто превышает рекомендуемую величину отклонения, равную 5%.

Поэтому приходится принимать ближайший больший размер двутавра, а именно №45^а, у которого W_х=1430 см³. В этом случае балка будет работать с недонапряжением:

что меньше [σ]=160МПа на  

Итак, принимается двутавр №45^а, у которого: W_х=1430 см³, I_х=32240см⁴, I_х: S_х=38,6см, d=11,5мм.

Далее необходима проверка прочности по касательным напряжениям с помощью условия прочности :

 

Это условие прочности выполняется, даже с избыточным запасом.

 

Задача 5

Подобрать сечение балки, рассмотрев шесть вариантов форм и три вида материалов (древесина, чугун, сталь).

Решение 

1.Определение опорных реакций 

∑М(А) = F · 2 + М₁ — М₂— q·6·7 + В · 8 =0,∑М(В) = F · 10 + М₁— М₂ – А · 8 + q·6·1 =0,Проверка:

∑у = – 20 – 40 ·6 +50+210 = — 260 + 260 ≡ 0.

2.Построение эпюр изгибающих моментов и поперечных сил.

I участок

∑М(С) = М(z₁) + F·z₁=0,

М(z₁) = — F·z₁= -20·z₁.

При z₁=0:     М = 0,

        z₁=2м:  М = – 40кНм,

∑у= — F— Q(z₁) = 0,

Q(z₁) = — 20кН.

II участок

        z₂=0:      М = — 20 – 40 = -60 кНм,

z₂=4м:   М = 200 — 20 – 120 = 200 — 140 = 60кНм.

∑у=- F + А — Q(z₂) = 0,

Q =- F + А= -20+50=30кН.

III участок

— парабола.

Приz₃=0:      М = — 20·4= — 80 кНм,

z₃=2м:   М = 210·2 — 20·(2+2)² = 420 – 320 = 100кНм,

z₃=4м:   М = 210·4 – 20 · (2+4)² = 840 – 720 = 120кНм.

∑у= Q(z₃) + В — q·(2+z₃) = 0,

Q(z₃) = — В + q·(2+z₃) = — 210 + 40·(2+z₃) – уравнение прямой.

Приz₃ = 0:       Q = -130кН,

        z₃ = 4м:     Q = 30кН.

Q(z₀) = — 210 + 40·(2+z₀) = 0,

— 210 + 80 + 40·z₀ = 0,

40·z₀ = 130,

z₀ =3,25м,

IV участок

парабола.

Приz₄=0:      М = 0 кНм,

z₄=1м:   М = – 20кНм,

z₄=2м:   М = — 80кНм.

∑у=- q·z₄ + Q(z₄) = 0,

Q(z₄) =q·z₄ = 40·z₄  – уравнение прямой,

        z₄ = 0:        Q = 0,

        z₄ = 2м:     Q = 80кН.

3. Подбор сечений (опасное сечение по σ: |_maxМ|=131,25кНм,

опасное сечение по τ: |_maxQ|=130кН).

Вариант 1. Деревянное прямоугольное ([σ]=15МПа, [τ]=3МПа)

Принимаем: В=0,24м,

                         Н=0,48м.

Проверяем по τ:

Вариант 2. Деревянное круглое

Принимаем d=0,45м,

Проверяем по τ:

Вариант 3. Чугун : ([σ_Р]=30МПа, [σ_с]=120МПа, [τ]=15МПа)

Принимаем b=0,19м, тогда h=0,38м, d=0,076м.

Проверка по τ:

b(у)= b — d= 0,19 — 0,076 = 0,114м

Вариант 4. Сталь, двутавр : ([σ]=160МПа, [τ]=80МПа).

по сортаменту W_х=953см³. Это №40: I_x=19062см⁴, S_х=545см³, d=0,83см.

Проверка по τ:

Вариант 5. Сталь, круглая труба

Принимаем D=0,22м   →  d = 0,6·D =0,132м.

Проверка по τ:

Вариант 6. Сталь, прямоугольная труба  

b₁= b — 2t = b — 2·0,1b = 0,8b,

h₁= h — 2t  = 0,8h,

Принимаем b=0,13м, h=0,26м.

Проверка по τ:

Кстати: какое из сечений стальной балки выгодней по расходу материала?

Двутавр —  А = 72,6см² = 72,6·10^-4 = 0,00726м²,

круглая труба –

прямоугольная труба — 

Самый лёгкий: двутавр → самый выгодный с точки зрения изгиба.

 

Расчет прогиба балки методом начальных параметров

В этой статье будут рассмотрены основные нюансы расчета прогибов, методом начальных параметров, на примере консольной балки, работающей на изгиб. А также рассмотрим пример, где с помощью универсального уравнения, определим прогиб балки и угол поворота.

Теория по методу начальных параметров

Возьмем консольную балку, нагруженную сосредоточенной силой, моментом, а также распределенной нагрузкой. Таким образом, зададимся такой расчетной схемой, где присутствуют все виды нагрузок, тем самым, охватим всю теоретическую часть по максимуму. Обозначим опорные реакции в жесткой заделке, возникающие под действием внешней нагрузки:

Выбор базы и обозначение системы координат

Для балки выберем базу с левой стороны, от которой будем отсчитывать расстояния до приложения сил, моментов, начала и конца распределенной нагрузки. Базу обозначим буквой O и проведем через нее систему координат:

Базу традиционно выбирают с левого краю балки, но можно выбрать ее и справа. Тогда в уравнении будут противоположные знаки, это может пригодиться в некоторых случаях, упростит  немного решение. Понимание, когда принимать базу слева или справа, придет с опытом решения задач на метод начальных параметров.

Универсальное уравнение прогибов для балки

После введения базы, системы координат и обозначении расстояний а, б, в, г записываем универсальную формулу, с помощью которой, будем рассчитывать прогиб балки (вертикальное перемещение сечения K, находящегося на свободном торце балки): Теперь поговорим об этой формуле, проанализируем так сказать:

• E – модуль упругости;
• I – момент инерции;
• V_k – прогиб сечения K;
• V_O – прогиб сечения O;
• θ_O – угол поворота сечения О.

Не буду приводить вывод этой формулы, не хочу отпугивать читателей, продвинутые студенты могут ознакомиться с выводом самостоятельно в учебнике по сопромату. Я только расскажу об основных закономерностях этого уравнения и как записать его для любой балки постоянного сечения.

Итак, изучаем эту формулу с лева направо. В левой части уравнения обознается искомый прогиб, в нашем случае V_k, который дополнительно умножается на жесткость балки — EI:В уравнении всегда учитывается прогиб сечения балки, совпадающего с нашей базой EIV_O:

Также всегда учитывается угол поворота сечения совпадающего с выбранной базой. Причем, произведение EIθ_O всегда умножается на расстояние от базы до сечения, прогиб которого рассчитывается, в нашем примере — это расстояние г.

Следующие компоненты этого уравнения учитывают всю нагрузку находящуюся слева от рассматриваемого сечения. В скобках расстояния от базы до сечения отнимаются расстояния от базы до соответствующей силы или момента, начала или конца распределенной нагрузки.

Скобка, в случае с сосредоточенными силами, возводится в 3 степень и делится на 6. Если сила смотрит вверх, то считаем ее положительной, если вниз, то в уравнении она записывается с минусом:

В случае с моментами, скоба возводится во 2 степень и делится на 2. Знак у момента будет положительный, когда он направлен почасовой стрелке и отрицательным, соответственно, когда против часовой стрелки.

Учет распределенной нагрузки

Теперь поговорим о распределенной нагрузке. Как уже говорилось, в уравнении метода начальных параметров должно учитываться начало и конец распределенной нагрузки, но конец ее совпадает с сечением, прогиб которого мы хотим вычислить, поэтому в уравнение попадает только ее начало.

Причем важно, даже если бы в этом сечении была бы сила или момент, их бы так же не учитывали. Нас интересует все, что находится слева от рассматриваемого сечения.

Для распределенной нагрузки скобочка возводится в 4 степень и делится на 24. Правило знаков такое же, как и для сосредоточенных сил:

Граничные условия

Чтобы решить уравнение нам понадобятся еще кое-какие данные. С первого взгляда в уравнении у нас наблюдается три неизвестных: V_K, VO и θ_O. Но кое-что мы можем почерпнуть из самой схемы. Мы знаем, в жесткой заделке не может быть никаких прогибов, и ни каких поворотов, то есть V_O=0 и θ_O=0, это и есть так называемые начальные параметры или их еще называют граничными условиями. Теперь, если бы у нас была реальная задача, мы бы подставили все численные данные и нашли перемещение сечения K.

Если бы балка была закреплена с помощью шарнирно подвижной и неподвижной опоры, тогда мы бы приняли прогибы в опорах равными нулю, но угол поворота в опорах был бы уже отличен от нуля. Более подробно об этом рассказано в другой моей статье, посвященной методу начальных параметров на примере балки на двух опорах.

Чуть не забыл про еще одну величину, которую часто требуется определять методом начальных параметров.  Как известно, при изгибе, поперечные сечения балок помимо того, что перемещаются вертикально (прогибаются) так еще и поворачиваются на какой-то угол. Углы поворота и прогибы поперечных сечений связаны дифференциальной зависимостью.

Если продифференцировать уравнение, которое мы получили для прогиба поперечного сечения K, то получим уравнение угла поворота этого сечения:

Пример расчета прогиба балки

Для закрепления пройденного материала, предлагаю рассмотреть пример с заданными численными значениями всех параметров балки и нагрузок. Возьмем также консольную балку, которая жестко закреплена с правого торца. Будем считать, что балка изготовлена из стали (модуль упругости E = 2·10⁵ МПа), в сечении у нее двутавр №16 (момент инерции по сортаменту I = 873 см⁴). Рассчитывать будем прогиб свободного торца, находящегося слева.

Подготовительный этап

Проводим подготовительные действия, перед расчетом прогиба: помечаем базу O, с левого торца балки, проводим координатные оси и показываем реакции, возникающие в заделке, под действием заданной нагрузки:

В методе начальных параметров, есть еще одна особенность, которая касается распределенной нагрузки. Если на балку действует распределенная нагрузка, то ее конец, обязательно должен находиться на краю балки (в точке наиболее удаленной от заданной базы). Только в таком случае, рассматриваемый метод будет работать. В нашем примере, нагрузка, как видно, начинается на расстоянии 2 м. от базы и заканчивается на 4 м. В таком случае, нагрузка продлевается до конца балки, а искусственное продление компенсируется дополнительной, противоположно-направленной нагрузкой. Тем самым, в расчете прогибов будет уже учитываться 2 распределенные нагрузки:

Расчет прогиба

Записываем граничные условия для заданной расчетной схемы:

V_A = 0 при x = 6м

θ_A = 0 при x = 6м

Напомню, что нас, в этом примере, интересует прогиб сечения O (V_O). Для его нахождения составим уравнение, для сечения A, в которое будет входить искомая величина:

В полученном уравнении, у нас содержится две неизвестные величины: искомый прогиб V_O и угол поворота этого сечения — θ_O:

Таким образом, чтобы решить поставленную задачу, составим дополнительное уравнение, но только теперь, не прогибов, а углов поворотов, для сечения A:Из второго уравнения, найдем угол поворота:После чего, рассчитываем искомый прогиб:

Таким образом, свободный торец такой балки, прогнется практически на 6 см. Данную задачу, можно решить несколько проще, если ввести базу с правого торца. В таком случае, для решения потребовалось бы лишь одно уравнение, однако, оно было бы немного объемнее, т.к. включало реакции в заделке.

Расчет балок на прогиб. Максимальный прогиб балки: формула

Балка – элемент в инженерии, представляющий собой стержень, который нагружают силы, действующие в направлении, перпендикулярном стержню. Деятельность инженеров зачастую включает в себя необходимость расчета прогиба балки под нагрузкой. Этой действие выполняется для того, чтобы ограничить максимальный прогиб балки.

Типы

На сегодняшний день в строительстве могут использоваться балки, изготовленные из разных материалов. Это может быть металл или дерево. Каждый конкретный случай подразумевает под собой разные балки. При этом расчет балок на прогиб может иметь некоторые отличия, которые возникают по принципу разницы в строении и используемых материалов.

Деревянные балки

Сегодняшнее индивидуальное строительство подразумевает под собой широкое применение балок, изготовленных из дерева. Практически каждое строение содержит в себе деревянные перекрытия. Балки из дерева могут использоваться как несущие элементы, их применяют при изготовлении полов, а также в качестве опор для перекрытий между этажами.

Ни для кого не секрет, что деревянная, так же как и стальная балка, имеет свойство прогибаться под воздействием нагрузочных сил. Стрелка прогиба зависит от того, какой материал используется, геометрических характеристик конструкции, в которой используется балка, и характера нагрузок.

Допустимый прогиб балки формируется из двух факторов:

• Соответствие прогиба и допустимых значений.
• Возможность эксплуатации здания с учетом прогиба.

Проводимые при строительстве расчеты на прочность и жесткость позволяют максимально эффективно оценить то, какие нагрузки сможет выдерживать здание в ходе эксплуатации. Также эти расчеты позволяют узнать, какой именно будет деформация элементов конструкции в каждом конкретном случае. Пожалуй, никто не будет спорить с тем, что подробные и максимально точные расчеты – это часть обязанностей инженеров-строителей, однако с использованием нескольких формул и навыка математических вычислений можно рассчитать все необходимые величины самостоятельно.

Для того чтобы произвести правильный расчет прогиба балки, нужно также брать во внимание тот факт, что в строительстве понятия жесткости и прочности являются неразрывными. Опираясь на данные расчета прочности, можно приступать к дальнейшим расчетам относительно жесткости. Стоит отметить, что расчет прогиба балки – один из незаменимых элементов расчета жесткости.

Обратите ваше внимание на то, что для проведения таких вычислений самостоятельно лучше всего использовать укрупненные расчеты, прибегая при этом к достаточно простым схемам. При этом также рекомендуется делать небольшой запас в большую сторону. Особенно если расчет касается несущих элементов.

Расчет балок на прогиб. Алгоритм работы

На самом деле алгоритм, по которому делается подобный расчет, достаточно прост. В качестве примера рассмотрим несколько упрощенную схему проведения расчета, при этом опустив некоторые специфические термины и формулы. Для того чтобы произвести расчет балок на прогиб, необходимо выполнить ряд действий в определенном порядке. Алгоритм проведения расчетов следующий:

• Составляется расчетная схема.
• Определяются геометрические характеристики балки.
• Вычисляется максимальную нагрузку на данный элемент.
• В случае возникновения необходимости проверяется прочность бруса по изгибающему моменту.
• Производится вычисление максимального прогиба.

Как видите, все действия достаточно просты и вполне выполнимы.

Составление расчетной схемы балки

Для того чтобы составить расчетную схему, не требуется больших знаний. Для этого достаточно знать размер и форму поперечного сечения элемента, пролет между опорами и способ опирания. Пролетом является расстояние между двумя опорами. К примеру, вы используете балки как опорные брусья перекрытия для несущих стен дома, между которыми 4 м, то величина пролета будет равна 4 м.

Вычисляя прогиб деревянной балки, их считают свободно опертыми элементами конструкции. В случае балки перекрытия для расчета принимается схема с нагрузкой, которая распределена равномерно. Обозначается она символом q. Если же нагрузка несет сосредоточенный характер, то берется схема с сосредоточенной нагрузкой, обозначаемой F. Величина этой нагрузки равна весу, который будет оказывать давление на конструкцию.

Момент инерции

Геометрическая характеристика, которая получила название момент инерции, важна при проведении расчетов на прогиб балки. Формула позволяет вычислить эту величину, мы приведем ее немного ниже.

При вычислении момента инерции нужно обращать внимание на то, что размер этой характеристики зависит от того, какова ориентация элемента в пространстве. При этом наблюдается обратно пропорциональная зависимость между моментом инерции и величиной прогиба. Чем меньше значение момента инерции, тем больше будет значение прогиба и наоборот. Эту зависимость достаточно легко отследить на практике. Каждый человек знает, что доска, положенная на ребро, прогибается гораздо меньше, чем аналогичная доска, находящаяся в нормальном положении.

Подсчет момента инерции для балки с прямоугольным сечением производится по формуле:

J=b*h^3/12, где:

b – ширина сечения;

h – высота сечения балки.

Вычисления максимального уровня нагрузки

Определение максимальной нагрузки на элемент конструкции производится с учетом целого ряда факторов и показателей. Обычно при вычислении уровня нагрузки берут во внимание вес 1 погонного метра балки, вес 1 квадратного метра перекрытия, нагрузку на перекрытие временного характера и нагрузку от перегородок на 1 квадратный метр перекрытия. Также учитывается расстояние между балками, измеренное в метрах. Для примера вычисления максимальной нагрузки на деревянную балку примем усредненные значения, согласно которым вес перекрытия составляет 60 кг/м², временная нагрузка на перекрытие равна 250 кг/м², перегородки будут весить 75 кг/м². Вес самой балки очень просто вычислить, зная ее объем и плотность. Предположим, что используется деревянная балка сечением 0,15х0,2 м. В этом случае ее вес будет составлять 18 кг/пог.м. Также для примера примем расстояние между брусьями перекрытия равным 600 мм. В этом случае нужный нам коэффициент составит 0,6.

В результате вычисления максимальной нагрузки получаем следующий результат: q=(60+250+75)*0,6+18=249 кг/м.

Когда значение получено, можно переходить к расчету максимального прогиба.

Вычисление значения максимального прогиба

Когда проводится расчет балки, формула отображает в себе все необходимые элементы. При этом стоит учитывать, что формула, используемая для расчетов, может иметь несколько иной вид, если расчет проводится для разных типов нагрузок, которые будут оказывать влияние на балку.

Сначала приведем вашему вниманию формулу, используемую для расчета максимального прогиба деревянной балки с распределенной нагрузкой.

f=-5*q*l^4/384*E*J.

Обратите внимание, что в данной формуле Е – это постоянная величина, которая получила название модуль упругости материала. Для древесины эта величина равна 100 000 кгс/ м².

Продолжив вычисления с нашими данными, использованными для примера, получим то, что для балки из древесины, сечение которой составляет 0,15х0,2 м, а длина равна 4 м, величина максимального прогиба при воздействии распределенной нагрузки равна 0,83 см.

Обращаем внимание, что когда производится расчет прогиба с учетом схемы с сосредоточенной нагрузкой, формула приобретает следующий вид:

f=-F*l^3/48*E*J, где:

F – сила давления на брус.

Также обращаем внимание на то, что значение модуля упругости, используемое в расчетах, может различаться для разных видов древесины. Влияние оказывают не только порода дерева, но и вид бруса. Поэтому цельная балка из дерева, клееный брус или оцилиндрованное бревно будут иметь разные модули упругости, а значит, и разные значения максимального прогиба.

Вы можете преследовать разные цели, совершая расчет балок на прогиб. Если вы хотите узнать пределы деформации элементов конструкции, то по завершении расчета стрелки прогиба вы можете остановиться. Если же ваша цель – установить уровень соответствия найденных показателей строительным нормам, то их нужно сравнить с данными, которые размещены в специальных документах нормативного характера.

Двутавровая балка

Обратите внимание на то, что балки из двутавра применяются несколько реже в силу их формы. Однако также не стоит забывать, что такой элемент конструкции выдерживает гораздо большие нагрузки, чем уголок или швеллер, альтернативой которых может стать двутавровая балка.

Расчет прогиба двутавровой балки стоит производить в том случае, если вы собираетесь использовать ее в качестве мощного элемента конструкции.

Также обращаем ваше внимание на то, что не для всех типов балок из двутавра можно производить расчет прогиба. В каких же случаях разрешено рассчитать прогиб двутавровой балки? Всего таких случаев 6, которые соответствуют шести типам двутавровых балок. Эти типы следующие:

• Балка однопролетного типа с равномерно распределенной нагрузкой.
• Консоль с жесткой заделкой на одном конце и равномерно распределенной нагрузкой.
• Балка из одного пролета с консолью с одной стороны, к которой прикладывается равномерно распределенная нагрузка.
• Однопролетная балка с шарнирным типом опирания с сосредоточенной силой.
• Однопролетная шарнирно опертая балка с двумя сосредоточенными силами.
• Консоль с жесткой заделкой и сосредоточенной силой.

Металлические балки

Расчет максимального прогиба одинаковый, будь это стальная балка или же элемент из другого материала. Главное — помнить о тех величинах, которые специфические и постоянные, как к примеру модуль упругости материала. При работе с металлическими балками, важно помнить, что они могут быть изготовлены из стали или же из двутавра.

Прогиб металлической балки, изготовленной из стали, вычисляется с учетом, что константа Е в данном случае составляет 2·105Мпа. Все остальные элементы, вроде момента инерции, вычисляются по алгоритмам, описанным выше.

Расчет максимального прогиба для балки с двумя опорами

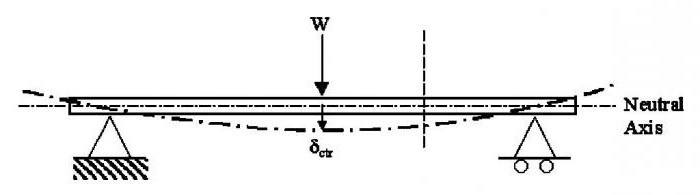
В качестве примера рассмотрим схему, в которой балка находится на двух опорах, а к ней прикладывается сосредоточенная сила в произвольной точке. До момента прикладывания силы балка представляла собой прямую линию, однако под воздействием силы изменила свой вид и вследствие деформации стала кривой.

Предположим, что плоскость ХУ является плоскостью симметрии балки на двух опорах. Все нагрузки действуют на балку в этой плоскости. В этом случае фактом будет то, что кривая, полученная в результате действия силы, также будет находиться в этой плоскости. Данная кривая получила название упругой линии балки или же линии прогибов балки. Алгебраически решить упругую линию балки и рассчитать прогиб балки, формула которого будет постоянной для балок с двумя опорами, можно следующим образом.

Прогиб на расстоянии z от левой опоры балки при 0 ≤ z ≤ a

F(z)=(P*a²*b²)/(6E*J*l)*(2*z/a+z/b-z³/a²*b)

Прогиб балки на двух опорах на расстоянии z от левой опоры при а ≤ z ≤l

f(z)=(-P*a²*b²)/(6E*J*l)*(2*(l-z)/b+(l-z)/a-(l-z)³/a+b²), где Р – прикладываемая сила, Е – модуль упругости материала, J – осевой момент инерции.

В случае балки с двумя опорами момент инерции вычисляется следующим образом:

J=b₁h₁³/12, где b₁ и h₁ – значения ширины и высоты сечения используемой балки соответственно.

Заключение

В заключение можно сделать вывод о том, что самстоятельно вычислить величину максимального прогиба балки разных типов достаточно просто. Как было показано в этой статье, главное — знать некоторые характеристики, которые зависят от материала и его геометрических характеристик, а также провести вычисления по нескольким формулам, в которых каждый параметр имеет свое объяснение и не берется из ниоткуда.