Прямой угол как начертить: Прямой угол. Построение прямого угла. Видеоурок. Математика 2 Класс – Как начертить прямой угол 🚩 построение прямого угла 🚩 Математика

Прямой угол. Построение прямого угла. Видеоурок. Математика 2 Класс

 Посмотрите на картинку. (Рис. 1)

Рис. 1. Иллюстрация к примеру

Из каких знакомых вам геометрических фигур она состоит?

 

Конечно, вы увидели, что картинка состоит из треугольников и прямоугольников. Какое слово спряталось в названии обеих этих фигур? Это слово – угол (рис. 2).

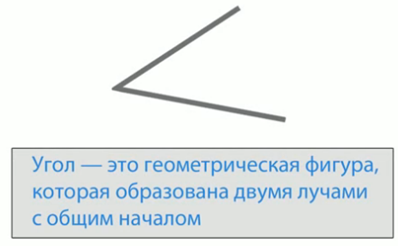
Рис. 2. Определение угла

Сегодня мы будем учиться чертить прямой угол.

В названии этого угла уже есть слово «прямой». Чтобы правильно изобразить прямой угол, нам понадобится угольник. (Рис. 3)

Рис. 3. Угольник

В самом угольнике уже есть прямой угол. (Рис. 4)

Рис. 4. Прямой угол

Он и поможет нам изобразить эту геометрическую фигуру.

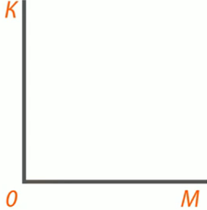
Чтобы правильно изобразить фигуру, мы должны приложить угольник к плоскости (1), обвести его стороны (2), назвать вершину угла (3) и лучи (4).

1.

2.

3.

4.

Давайте определим, есть ли среди имеющихся углов прямые (Рис. 5). В этом нам поможет угольник.

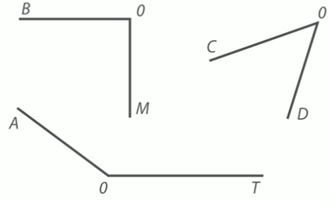
Рис. 5. Иллюстрация к примеру

Найдем прямой угол угольника и приложим его к имеющимся углам (рис. 6).

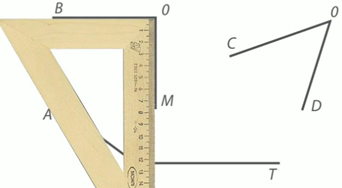
Рис. 6. Иллюстрация к примеру

Мы видим, что прямой угол совпал с углом ВОМ. Это значит, что угол ВОМ прямой. Проделаем эту же операцию еще раз. (Рис. 7)

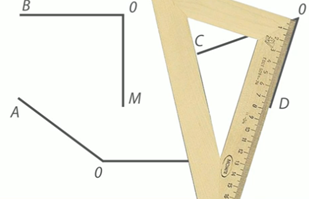
Рис. 7. Иллюстрация к примеру

Мы видим, что прямой угол нашего угольника не совпал с углом СOD. Это значит, что угол COD не прямой. Еще раз приложим прямой угол угольника к углу АОТ. (Рис. 8)

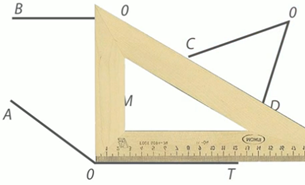
Рис. 8. Иллюстрация к примеру

Мы видим, что угол АОТ гораздо больше, чем прямой угол. Это значит, что угол АОТ не является прямым.

На этом уроке мы учились строить прямой угол с помощью угольника.

Слово «угол» дало название многим вещам, а также геометрическим фигурам: прямоугольник, треугольник, угольнику, с помощью которого можно начертить прямой угол.

Треугольник – это геометрическая фигура, которая состоит из трех сторон и трех углов. Треугольник, у которого есть прямой угол, называется прямоугольным треугольником.

 

Список литературы

1. Александрова Э.И. Математика. 2 класс. – М.: Дрофа, 2004.
2. Башмаков М.И., Нефёдова М.Г. Математика. 2 класс. – М.: Астрель, 2006.
3. Дорофеев Г.В., Миракова Т.И. Математика. 2 класс. – М.: Просвещение, 2012.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Сайт учителя начальных классов Сиразетдиновой Ляйсан Зуфаровны (Источник).
2. Социальная сеть работников образования nsportal.ru (Источник).
3. Социальная сеть работников образования nsportal.ru (Источник).

 

Домашнее задание

1. Выберите из предложенных углов прямые:

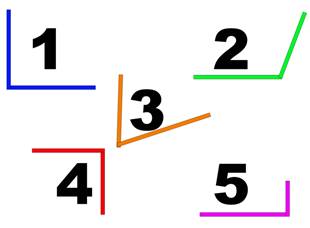
Рис. 9

2. Докажите, что изображенный на рисунке 10 угол – прямой.

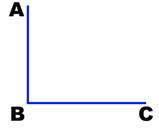
Рис. 10

Как построить прямой угол на местности – линейка без прямых углов

Соблюдайте правило прямого угла

Важную информацию о взаимоотношениях людей дает не только расстояние между ними, но и то, под каким углом они стоят или сидят по отношению друг к другу. Оптимальный вариант – это расположение друг к другу под углом 90 градусов.

Правило прямого угла

Мысленно нарисуйте прямоугольный треугольник и представьте, что вы с собеседником стоите на его катетах лицом в центр треугольника. Это открытая позиция. Вы повернуты друг к другу, но перед вами остается свободное пространство для «маневра». Общаясь и постепенно узнавая друг друга, вы сможете доверительно развернуться уже лицом к лицу.

Этот прием всем мужчинам рекомендую использовать при знакомстве с женщиной! Вы должны подойти к ней не лицом к лицу, а сбоку, чтобы между вами образовался угол в 90 градусов. Затем, в процессе беседы, вы можете постепенно разворачивать корпус, чтобы оказаться лицом к лицу, и при этом уменьшать дистанцию между вами. Но только постепенно! Если вы поторопитесь, женщина воспримет это как наглое домогательство. А если будете терпеливы – у вас появится хороший шанс пригласить ее на свидание!

Объяснить действие правила прямого угла проще всего на конкретном примере.

…

Представьте себе, что вы идете по улице, и вдруг к вам обращается человек с просьбой показать, например, какой-то дом. Вы останавливаетесь, чтобы подсказать правильное направление. Куда будет развернут ваш корпус: по направлению движения или к остановившему вас человеку? Правильно: в ту сторону, куда вы и направлялись!

А теперь другой вариант. Снова вы идете по улице и вас окликают, но это – о боже, какая встреча! – ваш старый приятель. Вы останавливаетесь, чтобы поздороваться, перекинуться парой слов и бежать дальше по своим делам. Теперь в какую сторону будет развернут ваш корпус? Конечно же, к приятелю!

В первом случае вы не разворачиваетесь полностью к человеку, потому что он не знаком вам. Ваше подсознание, основная задача которого – биологическая защита, знает, что положение боком по отношению к другому человеку уменьшает площадь поражения при возможном нападении.

Если же мы доверяем собеседнику и хотим с ним общаться, мы неосознанно поворачиваемся к нему – лицом к лицу. Потому что подсознание уверено: угрозы нападения нет.

Так что, если вы хотите найти общий язык с незнакомым собеседником, используйте правило прямого угла – треугольную диспозицию. И почаще обращайте внимание на то, как расположены ваши тела во время общения. Когда вы начинаете доверять друг другу, вы автоматически поворачиваетесь друг к другу лицом к лицу.

Добавлю еще одну маленькую хитрость. Если вы хотите убедить человека в чем-либо, стойте с левой стороны от него – там, где сердце. Доказано, что левая сторона более восприимчива к информации. Неслучайно цыганки на улице, когда подходят погадать, стараются встать с левой стороны, берут левую руку и тихим голосом нашептывают в левое ухо свои предсказания.

Поступайте так же – и будет вам счастье, к гадалке не ходи!

Следите за сигналами собеседника

Вспомните: иногда, общаясь с человеком, вы чувствуете, что он находится будто не с вами, не здесь. Вроде бы человек внимательно слушает вас, кивает головой, улыбается… Но вы ощущаете, что ваши слова пролетают мимо!

Внимание! Посмотрите на расположение тела вашего собеседника. Вы обязательно увидите, что либо поворот корпуса, либо носок ноги вашего партнера указывают в противоположную от вас сторону. Чаще всего к выходу из помещения, в котором вы общаетесь. Или направлены на другого человека, если вы общаетесь втроем.

Знайте: поворот корпуса и направление носка ноги всегда указывает на настоящее направление мыслей вашего собеседника!

Негативные сигналы

Если, проводя переговоры, вы вдруг заметили, что ваш собеседник откинулся назад, чуть отвернул корпус от вас, закинул ногу на ногу и остался в этом положении, срочно меняйте тактику поведения и общения!

Вы ошибаетесь, если думаете, что он расслабился и внимательно вас слушает. Ничуть! Наоборот, вы ему абсолютно неинтересны! Подобное положение тела является закрытым. Оно означает, что ваш собеседник закрылся от вас, удалился в мир своих мыслей.

Такие негативные сигналы могут означать для вас следующее:

• ваш собеседник услышал от вас нечто такое, что ему не понравилось;

• он понял, что ваша идея не представляет для него интереса;

• он уже принял решение отказать вам, не принимать ваше предложение.

Чтобы вновь заинтересовать вашего собеседника, рекомендую протянуть что-нибудь ему в руки. Таким образом он будет вынужден сменить позу, а вы должны использовать этот момент и сменить тактику ведения переговоров!

На что нужно обратить внимание? Во-первых, чтобы удержать внимание партнера, ваши движения и позы должны быть открытыми. Это значит, что ни в коем случае, никогда и ни при каких обстоятельствах, общаясь с людьми, вы не должны скрещивать руки и ноги. Это признак негативного или оборонительного отношения.

Ваша задача – научиться использовать положительные, открытые жесты для успешного общения с другими людьми. И, соответственно, избавиться от жестов закрытых, несущих отрицательную, негативную окраску. Используя открытые жесты, вы будете чувствовать себя более уютно в обществе людей и будете выглядеть более привлекательными для них.

Поза активного слушателя

Если вы хотите быть убедительными и одновременно внимательными к партнеру, обязательно освойте позу «активного слушателя». С ее помощью вы продемонстрируете свою заинтересованность в собеседнике!

Поставьте ноги прямо, параллельно друг другу. Корпус слегка подайте вперед, не откидывайтесь назад. Представьте, что вы слушаете увлекательную историю. Настолько интересную, что вы боитесь упустить даже слово. Поэтому не только ваше тело наклоняется вперед, но и голова слегка подается вперед и немного наклоняется вбок.

Потренируйтесь сперва на своих знакомых, чтобы ваши движения выглядели естественно. А оттачивать мастерство можно на совещаниях, собраниях и деловых встречах!

Концентрируйтесь на позитиве!

Чтобы все описанные выше приемы действовали наиболее эффективно, они должны выглядеть естественными.

Привязка зданий и сооружений к местности, разметка дома

Для этого ваше тело должно реагировать идеально в соответствии с вашими замыслами.

Как этого добиться? Самое простое – вспомнить такое состояние, когда вы чувствовали себя наиболее комфортно. Например, припомните, когда последний раз вы общались с близкими друзьями. Или сидели у камина на кресле-качалке под клетчатым пледом, с интересной книжкой в руках и мурлыкающей кошкой на коленях.

Заметили? Ваши губы расплываются в улыбке, взгляд смягчается, ладони раскрываются… Уверяю вас: при этом зрачки ваших глаз расширяются, а тело автоматически поворачивается к источнику тепла и уюта, будь то близкий человек или любимая кошка.

Это состояние нужно запомнить! И ощущение комфорта и уюта использовать при общении с незнакомым для вас человеком. Просто мысленно представьте, что этот человек – ваш друг, тот самый источник тепла и уюта. Вы очень рады его видеть! Ничего больше не требуется: ваше тело автоматически настроится на нужный лад.

Воспоминания о приятных переживаниях общения запускают цепную реакцию: от подсознательного смягчения взгляда до поворота тела. И все это происходит само собой!

Более того, когда вы ведете себя так, будто только что встреченный и пока незнакомый вам человек необычайно вам нравится, вы и в самом деле начинаете проникаться к нему искренней симпатией!

Это одно из правил психологии.

Когда мы верим, что нравимся другому человеку и что он нравится нам – наше поведение делает эти предположения реальностью. И то же самое происходит, когда мы верим, что не нравимся окружающим – это становится правдой!

Как говорил Генри Форд: «Верите ли вы, что не можете, или верите, что можете – вы правы в обоих случаях».

Практика третьего шага

Запомните основные правила!

Обязательно зафиксируйте в памяти основные правила третьего шага. Чтобы лучше их запомнить, рекомендую записать правила на бумаге. Записав, вы точно сможете их запомнить! Запомнив, будете использовать в жизни. А используя эти правила, вы измените не только свое поведение, но и поведение своих собеседников и партнеров!

Напомню, правила простые: сохраняйте дистанцию, используйте треугольную диспозицию, стойте с левой стороны от собеседника и используйте при разговоре открытые жесты.

Наблюдайте за людьми

Поставьте себе задачу каждый день хотя бы 15 минут наблюдать за поведением людей при разговоре. Оценивайте расположение их тел по отношению друг к другу во время разговора, делайте выводы, набирайтесь опыта!

Шаг четвертый. Покажите ваши руки!

Разметка фундамента с помощью штанов и паутины — просто о сложном

Чтобы дом стоял прочно на фундаменте, необходимо произвести тщательную разметку котлована и обеспечить восстановление границ периметра по окончании рытья траншей. Особенно это важно при использовании землеройной техники. По линиям разметки будет установлена опалубка, уложена арматура и залит раствор. Исправление ошибок, когда бетон затвердел, сложный и затратный процесс, его лучше избежать. В распоряжении строителя есть геодезические приборы, но можно обойтись простейшими инструментами и традиционными методами построения прямоугольников на земельном участке.

Гладко было на бумаге: делаем чертёж разметки

На первый взгляд, перенести план фундамента с чертежа на участок — задача простая. Вбил первый колышек и отмеряй от него. Как показывает практика, построить идеальный прямоугольник не у всех получается с первого раза, потому что:

• поверхность земли не является ровной;
• на расстояниях более 5 метров отклонения в доли градусов приводят к значительным погрешностям.

Ошибки выявляют контрольным замером сторон и диагоналей, когда выясняется:

• противоположные стороны равны, а диагонали нет — получился параллелограмм;
• диагонали равны, две стороны равны, а две другие нет — это признак равнобокой трапеции.

Вроде бы на глаз всё верно, но ошибки разметки на 10–20 см повлекут дальнейшие искажения, ведь фундамент — основа строения. Пройдут земляные работы, во время которых не исключены незначительные отклонения, особенно при использовании экскаватора и другой тяжёлой техники.

Выручает прямой угол. В параллелограмме и в равнобокой трапеции нет прямых углов. Ни одного. Задача сводится к тому, чтобы линии разметки были перпендикулярны друг другу. Школьный транспортир и треугольник не годятся. Они для чертежей на бумаге. Для топографической разметки потребуются другие инструменты.

Разметку котлована необходимо произвести до начала земляных работ

Способы разметки

Геометрия зародилась в античные времена, как наука построения фигур на плоскости для вычисления площади и объёма. Тогда же разработали основные аксиомы, теоремы и правила. Одна из теорем принадлежит Пифагору. Не одно тысячелетие она служит для построения прямых углов.

Пифагоровы штаны

Пифагор доказал теорему, построив на каждой стороне прямоугольного треугольника квадрат. Фигура получила шуточное название «Пифагоровы штаны».

Квадрат гипотенузы равен сумме квадратов катетов.

Самая известная иллюстрация теоремы — цифровой ряд 3, 4, 5.

Действительно, 3² + 4² = 5². Если взять три отрезки длиной 3, 4, 5 или равно кратные этим значениям, то при соединении таких отрезков получится прямоугольный треугольник. Разумеется, можно подобрать и другие числа, но на практике именно 3, 4, 5 оказались самыми удобными для построений.

Когда концы трёх отрезков совпадут, получится прямоугольный треугольник

Построение легко выполнить с помощью реек, подбирая длину под соотношение 3 : 4 : 5. Например, три рейки: одна 60 см, вторая 80 см, третья 1 метр. Если закрепить их концы, то стороны 60 и 80 см будут катетами, вдоль которых натягивают леску или шнур, обозначая границы траншеи. А гипотенуза в 1 м обеспечит общую прочность инструмента. Для этой же цели можно использовать бечёвку или шнур, длиной более 12 м. На бечёвке вяжут узелки через 3, 4 и 5 м и соединяют начало первого отрезка с концом третьего. В каждый узелок пропускают тонкий штырь. Теперь, если, удерживая за штыри, равномерно натянуть стороны, получим треугольник, подобный тому, который делали и в примере с рейками.

Видео: контроль разметки теоремой Пифагора

Метод паутины

Применение верёвочного треугольника привело к развитию метода паутины. В этом случае вяжут сразу прямоугольник с диагоналями и растягивают его на участке. В идеале длины отрезков бечёвки (шнура, шпагата) должны совпадать с размерами сторон и диагоналей фундамента, что практически редко осуществимо. Лучше взять оптимальное соотношение 6 : 8 : 10 метров для построения прямоугольников 6 х 8 м.

Метод паутины один из самых простых

При использовании «паутины» очень важно правильно выбрать бечёвку. Она должна быть свита из прядей, не изменяющих длину при натяжении. Такими свойствами обладают лён, пенька, джут, копра. Многие синтетические волокна, например, нейлон и капрон вытягиваются наподобие резины. Такой материал не подходит. Для надёжности делают контрольные замеры отрезка, увеличивая натяжение, чтобы убедиться в приемлемости бечёвки для вязки «паутины».

Видео: разметка с помощью двух рулеток

Метод радиусов и засечек

Прямоугольник можно построить засечками, проводя окружности радиусами равными длинам катетов и диагоналей. Вместо циркуля берут строительную 10-метровую рулетку. У неё есть ушко в начале ленты, куда вставляют заострённый штырь. Работать лучше втроём. Один держит рулетку на угловом колышке, второй прочерчивает дуги, третий контролирует натяжение ленты.

Видео: радиусы и засечки

Разметка фундамента своими руками

Знание методов недостаточно для точного нанесения границ фундамента. От первого вбитого колышка должны отойти не просто две перпендикулярные линии. Их направление определяется границами участка с учётом других объектов. Например, СНиП 30–02–97 требует, чтобы крайняя точка возводимого строения была не ближе 3 м к забору. Если крыша будет нависать 1 м над фундаментом, соответственно от фундамента до забора должно быть более 4 м.

В самом начале разметки фундамента важно выставить прямой угол между предполагаемыми стенами. Если этого не сделать сразу, то упущение может привести к плачевным результатам.

Дятька

https://www.forumhouse.ru/articles/house/5698

Для выверки границ котлована необязательно применять геодезические приборы. Можно обойтись простыми самодельными инструментами: размеченной верёвкой, треугольником из реек, нивелиром с уровнем, лазерной указкой, рулеткой.

Фотогалерея: инструменты для разметки фундамента

Стороны 0,6 х 0,8 х 1,0 м обеспечат прямой угол

Уровень с лазерной указкой — нивелир готов к работе

Узелки через 3, 4 и 5 м позволят построить прямоугольный треугольник

Для корректной работы с визиром потребуется вешка — тонкая высокая рейка

Разметку выполняют в следующей последовательности:

1. Сверяясь со СНиП 30–02–97, отмеряют допустимые расстояния от забора, улицы и других строений и определяют границы участка под разметку.
2. Забивают первый колышек. Пользуясь одним из методов, строят прямой угол.
3. От вершины угла отмеряют линии на длину сторон прямоугольника. Вбивают колышки.
4. От каждого колышка чертят прямой угол. На пересечении сторон забивают четвёртый колышек. Вершины прямоугольника построены. Определены внешние границы периметра разметки.
5. Производят контрольный замер противоположных сторон и диагоналей. Если равенство нарушено, проверяют, какой из углов не является прямым. Исправляют ошибку.

На следующем этапе нужно обозначить внутренние и внешние границы траншеи, а при неодходимости — линии, по которым будет возводиться опалубка внутри траншей.

Потребуются тонкие шнуры (шпагат, леска, капроновая нить, стальная проволока) и мерная скамеечка. В обиходе скамеечку также называют доской, рамой, обноской.

Мерная скамеечка или обноска служит для крепления шнуров, отмечающих границы фундамента

Конструкция скамеечки может быть самой разной, чаще всего её выполняют в виде небольших козел. Как сколотить — это на усмотрение домашнего мастера. Главное, чтобы она прочно стояла на своём месте и выдерживала натяжение шнуров.

Последовательность второго этапа:

1. Устанавливают скамеечки на некотором расстоянии за пределами разметки, чтобы они не создавали помехи земляным работам.
2. Вдоль разметки выкладывают шнуры, крепят их на скамеечках и натягивают как струны.
3. Если внутри траншеи будет монтироваться опалубка, то соответственно на скамеечке закрепят дополнительные струны. Внутренними отметят линии опалубки, внешними — границы траншеи.

По внешним шнурам проведут земляные работы, по внутренним возведут опалубку

Когда рытьё траншеи производится вручную, шнуры располагают невысоко над землёй, чтобы они не мешали землекопам и в то же время позволяли контролировать работу. Дополнительно используют отвес, проверяя вертикальность профиля траншеи.

При использовании экскаватора поверх шнуров сыпят контрастный порошок — мел, известь, цемент, золу либо прочерчивают контур краской. Шнуры убирают, а мерные скамеечки метят флажками, чтобы водитель техники случайно не наехал. После того как экскаватор закончит рытьё, шнуры снова натягивают и проверяю корректность выполненных работ.

Видео: разметка своими руками

Арсенал разметчика можно пополнить другими инструментами. В комплекте столярных или токарных наборов найдётся угольник. Закрепить на нём уровень и две лазерные указки — точность будет не хуже, чем у теодолита. В школьных кабинетах математики есть транспортиры и треугольники таких размеров, с которыми можно работать непосредственно на участке для выверки прямых углов. Туристы, особенно те, кто увлекается водными походами, знакомы с азимутальным кругом и пеленгатором. Деревянная крестовина, на концах которой закреплены саморезы в качестве прицелов, станет отличным визиром, если тщательно контролировать уровнем и отвесом её положение в горизонтальной и вертикальной плоскостях.

Вдоль линий разметки натянуты шнуры, закрепленные на мерных скамеечках

Знание основ геометрии и методов нанесения разметки простейшими инструментами позволит без труда подготовить участок перед земляными работами. Однако следует помнить золотое правило — семь раз отмерь, а потом копай. Контрольная проверка сторон, диагоналей и углов — необходимое условие, при котором будет обеспечено точное соответствие границ фундамента с планом строения.

2 класс Урок-путешествие «Прямой угол. Построение прямого угла.»

Открытый урок во 2-ом классе.

Учитель: Жаворонкова Елена Владимировна

Вид урока. Урок изучения и первичного закрепления новых знаний.

Основные цели:

Задачи:

• дать определение угла, как геометрической фигуры;

• дать определение «острый угол», «тупой угол»;

• научить чертить заданный вид угла с помощью линейки и треугольника;

• научить делать модель прямого угла из листа бумаги

• закрепить вычислительные навыки.

• распознать углы в окружающей обстановке;

• развивать логическое и пространственное мышление;

• формирование первичных геометрических навыков, речевой культуры, мыслительных процессов;

• воспитание аккуратности, самостоятельности.

Оборудование: мультимедийный проектор, компьютер, экран, листы бумаги,

карточки Claro, математическая Палитра, листы для индивидуальной работы.

ХОД УРОКА

1. Организационный момент

• Ребята, у нас на уроке присутствуют гости. Поздоровайтесь с ними, пожалуйста!

• Сегодня нам предстоит путешествие. Сейчас вам надо будет узнать название страны, в которую лежит наш путь. (Слайд 1)

• Кто догадался? Правильно: «ГЕОМЕТРИЯ» (Слайд 2)

• Нашим проводником будет житель этой страны Веселый Уголок.

• А вы, ребята, знаете, кто живет в моей стране?( Геометрические фигуры) (Слайд 3) Назовите геометрические фигуры, которые вы видите. На какие группы можно разделить эти геометрические фигуры? Как одним словом назвать геометрические фигуры, у которых есть углы? Правильно, (Слайд 4) «многоугольники». Молодцы!

2. Устный счет

• Ребята, чтобы отправиться в путешествие, надо узнать тему урока. Перед вами лежат карточки для устного счета. Выполните по одному заданию на них, работая в парах, проверьте себя. Занесите результат в таблицу. Поменяйте карточку и повторите упражнение.

• Возьмите каждый в руки карточку для счета. Опишите ее форму. ( 4 стороны, 4 угла, они одинаковые) Форму какой геометрической фигуры она имеет? (прямоугольника)

• Прислушайтесь к слову «ПРЯМОУГОЛЬНИК». Какие слова в нем спрятались? (прямой и угол). Как вы думаете, почему эту фигуру так назвали? (наверно, ее углы называются прямыми)

• Веселый Уголок предлагает вам выполнить следующее задание и проверить себя. (дети устно дают ответы и за правильный ответ получают карточку с буквой)

Блиц-турнир

• Наибольшее четное двузначное число. (98) Л

• Какое число следует за числом 77? (78) О

• Число, состоящее из 5 дес. и 7 ед. (57) У

• Какое число предшествует 50? (49) Й

• Найдите сумму чисел 30 и 5. (35) О

• Целое 38, меньшая часть 7, найдите большую часть. (31)М

• Уменьшаемое 27, вычитаемое 7. Найдите значение разности. (20) Я

• Какое число состоит из 6 десятков и 5 единиц? (65) Г

• Сначала из корзины выложили 12 яблок, а потом ещё 4. Сколько яблок выложили? (16)Р

• Наибольшее однозначное число. (9) П

Дети выстраиваются в ряд по порядку возрастания чисел на карточках с буквами. Читают: «Прямой угол». (Слайд 6) Веселый Уголок говорит: «Правильно, молодцы! Это и есть тема нашего урока-путешествия!»

Физкультминутка:

— Подпрыгните столько раз, сколько букв в слове «прямой».
— Присядьте столько раз, сколько букв в слове «угол».

3. Работа над новой темой

Ребята, представьте себе, что искусные кондитеры страны Геометрии испекли красивый круглый торт. Вам захотелось попробовать его. Каждый отрезал кусок. Если сверху посмотреть на этот кусок, что получится? (Модель угла)

Работа в парах с математической Палитрой:

Возьмите Палитру и представьте эту ситуацию. При помощи двух карандашей покажите свой воображаемый кусок.

— Одинаковые углы у вас получились?

— Веселый Уголок просит напомнить, из чего состоит любой угол? (Это два луча с общим началом в одной точке. Точка, из которой выходят лучи, называется вершиной угла. Лучи – стороны угла.) (Слайд 7):

— Угол – это часть плоскости, ограниченная двумя лучами, выходящими из одной точки. (Слайд 8)

— Чтобы продолжить наше путешествие, выполните задание на вашей Палитре. Результат занесите в таблицу.

Практическая работа (у учеников листы бумаги)

• Ребята, а какой именно угол сегодня нас интересует? (Прямой)

• Сейчас мы с вами изготовим модель прямого угла из бумаги

• Откройте учебники на с.24 и прочитайте, как это сделать

• Кто понял и может объяснить? ( ученик выходит к доске и выполняет работу, объясняя всем)
  – Сложите лист пополам, сложите ещё раз пополам.
  – Модель угла готова.

• Отметим прямой угол особым знаком (Слайд 9)

• Рассмотрите свои модели углов. Сравните с соседом по парте методом наложения. Что наблюдаете?

• Как называется угол, который мы отметили?

• У каждого из вас образовалась модель прямого угла. Приложите ее к углам карточек для устного счета. Что наблюдаете?

Физкультминутка:

Дети выполняют упражнения, имитируя прямой угол.

• Сгибают руки в кистях. В локтях.

• Сгибают ноги в коленях.

• Выполняют наклоны туловища.

Построение прямого угла при помощи чертежного угольника:

• Мы сделали модель прямого угла, а теперь научимся его строить на плоскости. Это удобно делать при помощи чертежного угольника. (Слайд 10) Рассмотрите чертежный угольник у себя на парте, найдите у него прямой угол.

• Положите перед собой лист бумаги. Проведите на нем прямую. Отметьте на ней точку. Приложите к этой точке вершину прямого угла вашего угольника, совместив одну его сторону с прямой, и постройте вторую сторону прямого угла. Покажите вершину вашего прямого угла.

• Чтобы определить, является ли данный угол прямым, нужно наложить угольник на угол так, чтобы у них совпали вершины и одна сторона. Если при этом совпадает и другая сторона, то данный угол – прямой, а если не совпадает, то данный угол не является прямым.

• Сравните модель прямого угла из бумаги , построенный прямой угол на плоскости и прямой угол угольника. Что наблюдаете?

• Посмотрите вокруг и назовите, где в классе есть прямые углы.

Работа на компьютерах в программе ПервоЛого:

• • построение прямой

  • построение точки на этой прямой

  • построение прямоугольника из этой точки на прямой

  • выделение прямого угла

  • построение острого угла

  • построение тупого угла

  • выделение острого и тупого угла

  • сохранение работы на Рабочий стол

4. Закрепление изученного:

Стихотворение (Слайд ):

Взяли чистый мы листок
И сложили уголок.
Угол вот такой у взрослых
Называется ПРЯМЫМ.
Если угол уже — ОСТРЫМ,
Если шире, то — ТУПЫМ.

Веселый Уголок прощается с вами!

Продолжите фразу:

• • Лучи – это стороны угла.

  • Общее начало лучей – вершина угла.

  • Угол, меньше прямого называется острым.

  • А угол, больше прямого называется тупым.

Самостоятельная работа по карточкам.

5. Итог урока. Рефлексия:

— О чем узнали на уроке?

— Чему научились?

— Какие задания были наиболее интересными?

— Кто доволен своей работой на уроке? Возьмите с Палитры зеленую фишку.

— Кто считает, что работал не во всю силу и хотел бы на следующий раз работать лучше – желтую фишку.

— Кто не доволен своей работой – красную фишку.

— Поднимите фишки. (Анализ результата)

— Спасибо за работу!

6. Домашнее задание:

— Придумать и нарисовать дом веселого уголочка из различных геометрических фигур. Обозначить прямые углы.

— в ВП принять участие в опросах:

— Вершина угла — это . . . а) точка, б) отрезок, в) луч

— Стороны угла – это … а) отрезки, б) лучи, в) прямые

— Острый угол … прямого. а) больше, б) меньше

— Тупой угол … прямого. а) меньше, б) больше

— Какого вида получается угол, если сложить лист бумаги пополам два раза? а) тупой,

б) острый, в) прямой

ПНШ 3 класс. Математика. Учебник № 1, с. 121

Как измерить угол

Ответы к с. 121

407. Миша и Маша делали аппликации веера из одинаковых бумажных «лепестков». Слева нарисована аппликация, которую сделал Миша, а справа — которую сделала Маша.

У кого из детей получился веер, который раскрыт на больший угол?
Как это можно узнать? Измерь каждый из углов с помощью угла-«лепестка» и назови результат. В тетради отметь красным цветом угол, состоящий из трёх углов-«лепестков».

Чтобы узнать, чей веер раскрыт на больший угол, необходимо наложить угол-«лепесток» на веер Миши и Маши. В веер Миши входит 4 угла-«лепестка», а веер Маши — 6 таких углов-«лепестков». Значит, веер Маши раскрыт на больший угол.  

408. Начерти прямой угол в своей тетради. Измерь его с помощью угла-«лепестка».

Назови результат своему соседу по парте.

Угол-«лепесток» помещается в прямом угле 6 раз. Прямой угол 90 градусов, следовательно, величина угла-«лепестка» будет: 90 : 6 = 15 градусов. 

Ответы к заданиям. Математика. Учебник. Часть 1. Чекин А.Л. 2013 г.

Математика. 3 класс. Чекин А.Л.

2 / 5 ( 6 голосов )

Окружность. Задачи на построение — урок. Геометрия, 7 класс.

Окружность — геометрическая фигура, состоящая из всех точек плоскости, которые находятся на заданном расстоянии от данной точки.

Эту точку называют центром окружности, а заданное расстояние — радиусом окружности.

 

Радиус — это отрезок, соединяющий центр окружности с любой точкой окружности. Из определения следует, что можно провести бесконечное количество радиусов, и они все имеют одинаковую длину.

 

Отрезок, который соединяет две точки на окружности, называют хордой.

 

Если хорда проходит через центр окружности, то её называют диаметром окружности.

Диаметр — самая длинная хорда.

В окружности также можно провести бесконечное количество диаметров.

 

 

Если соединить две точки окружности не отрезком, а кривой, проходящей по самой окружности, то часть окружности между двумя точками называют дугой.

Если на окружности отметить две точки, то получаются две дуги. Поэтому для названия дуги используют три латинские буквы, которые могут быть как маленькие, так и большие.

 

На рисунке выше можем назвать: дуга \(BDH\), дуга \(ACG\) и другие.

На рисунке ниже нарисованы: дуга \(AxB\) и дуга \(AyB\).

 

Часть плоскости, ограниченная окружностью, называется кругом.

Задачи на построение

 

В задачах, где необходимо выполнить конструкции, используются циркуль и линейка.

Очень важно запомнить, что в этих задачах линейка используется не как инструмент для измерения, а исключительно только для того, чтобы провести прямую, луч или отрезок через две данные точки, то есть, чтобы провести прямую линию. Циркуль используется для построения окружности или дуги окружности.

 

Рассмотрим пять основных построений, в которых используем упомянутые действия — построение прямой линии и окружности:

 

1. на данном луче от его начала отложить отрезок, равный данному.
2. Построение угла, равного данному.
3. Построение биссектрисы угла.

4. Построение перпендикулярных прямых.
5. Построение середины отрезка.

 

1. На данном луче от его начала отложить отрезок, равный данному.
См. видео.

  

 

Ясно, что таким образом мы получили отрезок, равный данному. Соответственно определению окружности, она состоит из точек, расположенных на заданном расстоянии (радиусе) от некоей точки (центра окружности).

Если центром служит начальная точка луча \(C\), радиусом — данный отрезок \(AB\), то точка пересечения окружности и луча \(D\) и есть искомая конечная точка отрезка \(CD\), равного данному отрезку \(AB\).

 

2. Построение угла, равного данному.

См. видео.

  

Докажем, что построенный угол \(ECD\) и есть тот искомый угол, равный данному углу \(AOB\).

Если мы построили окружность с центром \(C\) — начальной точкой луча и таким же радиусом, как у окружности с центром \(O\), то \(CD\) \(=\) \(OB\).

Если далее мы построили окружность с центром \(D\) и радиусом, равным отрезку \(BA\), и получили точку пересечения обеих окружностей \(E\), то \(BA\) \(=\) \(DE\).

Провели луч \(CE\). Очевидно, \(OA\) \(=\) \(CE\).

Значит, треугольники \(AOB\) и \(ECD\) равны по третьему признаку равенства треугольников, у них равны и углы, в том числе угол \(ECD\) равен углу \(AOB\).

 

3. Построение биссектрисы угла.

См. видео.

  

 

Чтобы доказать, что \(OC\) действительно делит угол \(AOB\) пополам, достаточно рассмотреть треугольники \(AOC\) и \(BOC\). 

\(OA = OB\) как радиусы одной окружности, а \(AC = BC\), так как мы при построении выбрали одинаковые радиусы для обеих окружностей.

Сторона \(OC\) — общая.

Эти треугольники равны по третьему признаку.

Следовательно, их соответствующие углы равны.

Значит, \(AOC\) и \(BOC\) — две равные части одного угла, это означает, что луч \(OC\) делит угол пополам.

 

4. Построение перпендикулярных прямых.

См. видео.

  

 

Почему \(DE\) является перпендикулярной к \(BC\)?

\(AB = AC\) — так эти точки были отложены при построении.

\(BD = CD\), так как мы обе окружности построили с одинаковыми радиусами.

Значит, \(DA\) или \(EA\) — медианы, проведённые к основанию равнобедренных треугольников \(BDC\) или \(BEC\).

Медиана в равнобедренном треугольнике является также высотой, то есть перпендикулярна к основанию.

 

5. Построение середины отрезка.

См. видео.

  

 

Эта конструкция такая же, как в случае построения перпендикулярных прямых, и уже доказано, что \(DC\) или \(EC\) делит \(AB\) пополам, то есть \(C\) — серединная точка отрезка \(AB\).