Покрытие множества — Википедия
У этого термина существуют и другие значения, см. Покрытие (значения).Покры́тие в математике — семейство множеств, таких, что их объединение содержит заданное множество.
Обычно покрытия рассматривается в общей топологии, где наибольший интерес представляют открытые покрытия — семейства открытых множеств. В комбинаторной геометрии важную роль играют покрытия выпуклыми множествами[1].
Содержание
- 1 Определения
- 2 Связанные определения
- 3 Свойства
- 4 См. также
- 5 Примечания
Определения
- Пусть дано множество X{\displaystyle X}. Семейство множеств C={Uα}α∈A{\displaystyle C=\{U_{\alpha }\}_{\alpha \in A}} называется покрытием X{\displaystyle X}, если
- X⊂⋃α∈AUα.{\displaystyle X\subset \bigcup \limits _{\alpha \in A}U_{\alpha }.}
- Пусть дано топологическое пространство (X,T){\displaystyle (X,{\mathcal {T}})}, где X{\displaystyle X} — произвольное множество, а T{\displaystyle {\mathcal {T}}} — определённая на X{\displaystyle X} топология. Тогда семейство открытых множеств C={Uα}α∈A⊂T{\displaystyle C=\{U_{\alpha }\}_{\alpha \in A}\subset {\mathcal {T}}} называется
- Y⊂⋃α∈AUα.{\displaystyle Y\subset \bigcup \limits _{\alpha \in A}U_{\alpha }.}
Связанные определения
- Если C{\displaystyle C} — покрытие множества Y{\displaystyle Y}, то любое подмножество D⊂C{\displaystyle D\subset C}, также являющееся покрытием Y{\displaystyle Y}, называется подпокры́тием.
- Если каждый элемент одного покрытия является подмножеством какого-либо элемента второго покрытия, то говорят, что первое покрытие
- ∀β∈B∃α∈A{\displaystyle \forall \beta \in B\;\exists \alpha \in A} такое, что Vβ⊂Uα.{\displaystyle V_{\beta }\subset U_{\alpha }.}
- Покрытие C={Uα}α∈A{\displaystyle C=\{U_{\alpha }\}_{\alpha \in A}} множества Y{\displaystyle Y} называется лока́льно коне́чным, если для каждой точки y∈Y{\displaystyle y\in Y} существует окрестность U∋y{\displaystyle U\ni y}, пересекающаяся лишь с конечным числом элементов C{\displaystyle C}, то есть множество {α∈A∣Uα∩U≠∅}{\displaystyle \{\alpha \in A\mid U_{\alpha }\cap U\not =\varnothing \}} конечно.
- Покрытие C={Uα}α∈A{\displaystyle C=\{U_{\alpha }\}_{\alpha \in A}} множества Y{\displaystyle Y} называется фундамента́льным, если всякое множество, пересечение которого с каждым множеством U∈C{\displaystyle U\in C} открыто в Y{\displaystyle Y}, само открыто.
- Y{\displaystyle Y} называется компактным, если любое его открытое покрытие содержит конечное подпокрытие;
- Y{\displaystyle Y} называется паракомпактным, если в любое его открытое покрытие можно вписать локально конечное открытое покрытие.
Свойства
- Любое подпокрытие вписано в изначальное покрытие. Обратное, вообще говоря, неверно.
См. также
- Карта (математика)
- Нерв покрытия
- Размерность Лебега
Примечания
- ↑ Покрытие множества — статья из Математической энциклопедии. А. В. Архангельский, П. С. Солтан
Покрытие множества — Википедия
У этого термина существуют и другие значения, см. Покрытие.Покры́тие в математике — семейство множеств, таких, что их объединение содержит заданное множество.
Обычно покрытия рассматривается в общей топологии, где наибольший интерес представляют открытые покрытия — семейства открытых множеств. В комбинаторной геометрии важную роль играют покрытия выпуклыми множествами[1].
Содержание
- 1 Определения
- 2 Связанные определения
- 3 Свойства
- 4 См. также
- 5 Примечания
Определения
- Пусть дано множество X{\displaystyle X}. Семейство множеств C={Uα}α∈A{\displaystyle C=\{U_{\alpha }\}_{\alpha \in A}} называется покрытием X{\displaystyle X}, если
- X⊂⋃α∈AUα.{\displaystyle X\subset \bigcup \limits _{\alpha \in A}U_{\alpha }.}
- Пусть дано топологическое пространство (X,T){\displaystyle (X,{\mathcal {T}})}, где X{\displaystyle X} — произвольное множество, а T{\displaystyle {\mathcal {T}}} — определённая на X{\displaystyle X} топология. Тогда семейство открытых множеств C={Uα}α∈A⊂T{\displaystyle C=\{U_{\alpha }\}_{\alpha \in A}\subset {\mathcal {T}}} называется
- Y⊂⋃α∈AUα.{\displaystyle Y\subset \bigcup \limits _{\alpha \in A}U_{\alpha }.}
Связанные определения
- Если C{\displaystyle C} — покрытие множества Y{\displaystyle Y}, то любое подмножество D⊂C{\displaystyle D\subset C}, также являющееся покрытием Y{\displaystyle Y}, называется подпокры́тием.
- Если каждый элемент одного покрытия является подмножеством какого-либо элемента второго покрытия, то говорят, что первое покрытие впи́сано во второе. Более точно, покрытие D={Vβ}β∈B{\displaystyle D=\{V_{\beta }\}_{\beta \in B}} вписано в покрытие C={Uα}α∈A{\displaystyle C=\{U_{\alpha }\}_{\alpha \in A}}, если
- ∀β∈B∃α∈A{\displaystyle \forall \beta \in B\;\exists \alpha \in A} такое, что Vβ⊂Uα.{\displaystyle V_{\beta }\subset U_{\alpha }.}
- Покрытие C={Uα}α∈A{\displaystyle C=\{U_{\alpha }\}_{\alpha \in A}} множества Y{\displaystyle Y} называется лока́льно коне́чным, если для каждой точки y∈Y{\displaystyle y\in Y} существует окрестность U∋y{\displaystyle U\ni y}, пересекающаяся лишь с конечным числом элементов C{\displaystyle C}, то есть множество {α∈A∣Uα∩U≠∅}{\displaystyle \{\alpha \in A\mid U_{\alpha }\cap U\not =\varnothing \}} конечно.
- Покрытие C={Uα}α∈A{\displaystyle C=\{U_{\alpha }\}_{\alpha \in A}} множества Y{\displaystyle Y} называется фундамента́льным, если всякое множество, пересечение которого с каждым множеством U∈C{\displaystyle U\in C} открыто в Y{\displaystyle Y}, само открыто.
- Y{\displaystyle Y} называется компактным, если любое его открытое покрытие содержит конечное подпокрытие;
- Y{\displaystyle Y} называется паракомпактным, если в любое его открытое покрытие можно вписать локально конечное открытое покрытие.
Свойства
- Любое подпокрытие вписано в изначальное покрытие. Обратное, вообще говоря, неверно.
См. также
- Карта (математика)
- Нерв покрытия
- Размерность Лебега
Примечания
- ↑ Покрытие множества — статья из Математической энциклопедии. А. В. Архангельский, П. С. Солтан
Открытое покрытие — это… Что такое Открытое покрытие?
- Открытое покрытие
Покры́тие в математике — это семейство множеств таких, что их объединение содержит заданное множество. Обычно понятие покрытия рассматривается в контексте общей топологии.
Определения
- Пусть дано множество X. Семейство множеств
 называется покрытием X, если
называется покрытием X, если
Связанные определения
- Если C — покрытие множества Y, то любое подмножество
 , также являющееся покрытием Y, называется подпокры́тием.
, также являющееся покрытием Y, называется подпокры́тием. - Если каждый элемент одного покрытия является подмножеством какого либо элемента второго покрытия, то говорят, что первое покрытия впи́сано
 вписано в покрытие
вписано в покрытие  , если
, если
 такое, что
такое, что 
- Покрытие

 существует окрестность
существует окрестность  , пересекающаяся лишь с конечным числом элементов C, то есть множество
, пересекающаяся лишь с конечным числом элементов C, то есть множество  конечно.
конечно. - Y
- Y называется паракомпактным, если в любое его открытое покрытие можно вписать локально конечное открытое покрытие.
Свойства
- Любое подпокрытие вписано в изначальное покрытие. Обратное, вообще говоря, неверно.
См. также
- Пусть дано множество X. Семейство множеств
Wikimedia Foundation. 2010.
- Открытое отображение
- Открытое подмножество
Смотреть что такое «Открытое покрытие» в других словарях:
Покрытие — У этого термина существуют и другие значения, см. Покрытие (значения). Покрытие в математике это семейство множеств, таких, что их объединение содержит заданное множество. Обычно понятие покрытия рассматривается в контексте общей топологии … Википедия
Покрытие (математика) — У этого термина существуют и другие значения, см. Покрытие (значения). Покрытие в математике это семейство множеств, таких, что их объединение содержит заданное множество. Обычно понятие покрытия рассматривается в контексте общей топологии … Википедия
Покрытие (в геометрии) — Покрытие в математике это семейство множеств таких, что их объединение содержит заданное множество. Обычно понятие покрытия рассматривается в контексте общей топологии. Содержание 1 Определения 2 Связанные определения 3 Свойства … Википедия
Открытое отображение — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
ПОКРЫТИЕ — множества X любое семейство подмножеств этого множества, объединение к рого есть X. 1) Под П. топологического пространства, равномерного пространства и вообще какого либо множества, наделенного тем или иным строением, понимают произвольное П.… … Математическая энциклопедия
Локально конечное покрытие — Покрытие в математике это семейство множеств таких, что их объединение содержит заданное множество. Обычно понятие покрытия рассматривается в контексте общей топологии. Содержание 1 Определения 2 Связанные определения 3 Свойства … Википедия
ЛОКАЛЬНО КОНЕЧНОЕ ПОКРЫТИЕ — покрытиетопологич. пространства его подмножествами такое, что у каждой точки есть окрестность, пересекающаяся лишь с конечным числом элементов этого покрытия. Не из всякого открытого покрытия прямой можно выделить Л. к. п.: достаточно рассмотреть … Математическая энциклопедия
ПАРАКОМПАКТНОСТИ КРИТЕРИИ — следующие утверждения, равносильные для произвольного вполне регулярного хаусдорфова пространства X.1) Xпаракомпактно. 2) В каждое открытое покрытие пространства Xможно вписать локально конечное открытое покрытие. 3) В каждое открытое покрытие… … Математическая энциклопедия
ПАРАКОМПАКТНОЕ ПРОСТРАНСТВО — топологическое пространство, в любое открытое покрытие к рого можно вписать локально конечное открытое покрытие. (Семейство g множеств, лежащих в топологич. пространстве X, наз. локально конечным в X, если у каждой точки существует окрестность в… … Математическая энциклопедия
Топология — (от греч. tоpos место и …логия (См. …Логия) часть геометрии, посвященная изучению феномена непрерывности (выражающегося, например, в понятии предела). Разнообразие проявлений непрерывности в математике и широкий спектр различных… … Большая советская энциклопедия
Покрытие множества — Википедия
У этого термина существуют и другие значения, см. Покрытие (значения).Покры́тие в математике — семейство множеств, таких, что их объединение содержит заданное множество.
Обычно покрытия рассматривается в общей топологии, где наибольший интерес представляют открытые покрытия — семейства открытых множеств. В комбинаторной геометрии важную роль играют покрытия выпуклыми множествами[1].
Содержание
- 1 Определения
- 2 Связанные определения
- 3 Свойства
- 4 См. также
- 5 Примечания
Определения
- Пусть дано множество X{\displaystyle X}. Семейство множеств C={Uα}α∈A{\displaystyle C=\{U_{\alpha }\}_{\alpha \in A}} называется покрытием X{\displaystyle X}, если
- X⊂⋃α∈AUα.{\displaystyle X\subset \bigcup \limits _{\alpha \in A}U_{\alpha }.}
- Пусть дано топологическое пространство (X,T){\displaystyle (X,{\mathcal {T}})}, где X{\displaystyle X} — произвольное множество, а T{\displaystyle {\mathcal {T}}} — определённая на X{\displaystyle X} топология. Тогда семейство открытых множеств C={Uα}α∈A⊂T{\displaystyle C=\{U_{\alpha }\}_{\alpha \in A}\subset {\mathcal {T}}} называется открытым покрытием множества Y⊂X{\displaystyle Y
Покрытие множества Википедия
У этого термина существуют и другие значения, см. Покрытие.Покры́тие в математике — семейство множеств, таких, что их объединение содержит заданное множество.
Обычно покрытия рассматривается в общей топологии, где наибольший интерес представляют открытые покрытия — семейства открытых множеств. В комбинаторной геометрии важную роль играют покрытия выпуклыми множествами[1].
Содержание
- 1 Определения
- 2 Связанные определения
- 3 Свойства
- 4 См. также
- 5 Примечания
Определения[ | ]
- Пусть дано множество X{\displaystyle X}. Семейство множеств C={Uα}α∈A{\displaystyle C=\{U_{\alpha }\}_{\alpha \in A}} называется покрытием X{\displaystyle X}, если
- X⊂⋃α∈AUα.{\displaystyle X\subset \bigcup \limits _{\alpha \in A}U_{\alpha }.}
- Пусть дано топологическое пространство (X,T){\displaystyle (X,{\mathcal {T}})}, где X{\displaystyle X} — произвольное множество, а T{\displaystyle {\mathcal {T}}} — определённая на X{\displaystyle X} топология. Тогда семейство открытых множеств C={Uα}α∈A⊂T{\displaystyle C=\{U_{\alpha }\}_{\alpha \in A}\subset {\mathcal {T}}} называется открытым покрытием множества Y⊂X{\displaystyle Y\subset X}, если
Покрытие (математика) — это… Что такое Покрытие (математика)?
Покрытие (значения) — Покрытие: Покрытие (математика) семейство множеств, объединение которых содержит данное множество. Покрытие (конструкция) верхняя конструкция здания Покрытие (материал) поверхностный слой, материал Критерий тестового покрытия метрика в… … Википедия
Покрытие — У этого термина существуют и другие значения, см. Покрытие (значения). Покрытие в математике это семейство множеств, таких, что их объединение содержит заданное множество. Обычно понятие покрытия рассматривается в контексте общей топологии … Википедия
Покрытие (в геометрии) — Покрытие в математике это семейство множеств таких, что их объединение содержит заданное множество. Обычно понятие покрытия рассматривается в контексте общей топологии. Содержание 1 Определения 2 Связанные определения 3 Свойства … Википедия
Локально конечное покрытие — Покрытие в математике это семейство множеств таких, что их объединение содержит заданное множество. Обычно понятие покрытия рассматривается в контексте общей топологии. Содержание 1 Определения 2 Связанные определения 3 Свойства … Википедия
Открытое покрытие — Покрытие в математике это семейство множеств таких, что их объединение содержит заданное множество. Обычно понятие покрытия рассматривается в контексте общей топологии. Содержание 1 Определения 2 Связанные определения 3 Свойства … Википедия
Карта (математика) — Содержание 1 Карта 2 Согласованные карты 3 Покрытие пространства 4 Атлас … Википедия
Область (математика) — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
Схема (математика) — В алгебраической геометрии схема это абстракция, позволяющая связать единым образом коммутативную алгебру и дифференциальную геометрию и переносить идеи из одной области в другую. В первую очередь понятие схемы позволяет перенести… … Википедия
Задача о вершинном покрытии — NP полная задача информатики в области теории графов. Часто используется в теории сложности для доказательства NP полноты более сложных задач. Содержание 1 Определение 2 NP полнота 3 Ссылки … Википедия
Александр II (часть 2, XIII-XIX) — XIII. Дела внутренние (1866—1871). 4 го апреля 1866 года, в четвертом часу дня, Император Александр, после обычной прогулки в Летнем саду, садился в коляску, когда неизвестный человек выстрелил в него из пистолета. В эту минуту, стоявший в… … Большая биографическая энциклопедия
Подпокрытие — это… Что такое Подпокрытие?
Лемма Гейне — Леммой Гейне Бореля [1], а также леммой Бореля Лебега [2] называется следующий факт, играющий фундаментальную роль в анализе: Из всякой бесконечной системы интервалов, покрывающей отрезок числовой прямой, можно выбрать конечную подсистему, также… … Википедия
Лемма Гейне — Бореля — Леммой Гейне Бореля [1], а также леммой Бореля Лебега [2] называется следующий факт, играющий фундаментальную роль в анализе: Из всякой бесконечной системы интервалов, покрывающей отрезок числовой прямой, можно выбрать конечную подсистему, также… … Википедия
Теорема Александера о предбазе — Теорема Александера о предбазе[1] (англ. Alexander Subbase Theorem) теорема общей топологии, устанавливающая критерий компактности топологического пространства. Компактным называется пространство, допускающая выделение из каждого своего… … Википедия
ПОКРЫТИЕ — множества X любое семейство подмножеств этого множества, объединение к рого есть X. 1) Под П. топологического пространства, равномерного пространства и вообще какого либо множества, наделенного тем или иным строением, понимают произвольное П.… … Математическая энциклопедия
Глоссарий общей топологии — Эта страница глоссарий. См. также основную статью: Общая топология В этом глоссарии приведены определения основных терминов, используемых в общей топологии. Курсивом выделены ссылки внутри глос … Википедия
БИКОМПАКТНОЕ ПРОСТРАНСТВО — топологическое пространство, в каждом открытом покрытии к рого содержится конечное подпокрытие того же пространства. Следующие утверждения равносильны: 1) пространство Xбикомпактно; 2) пересечение любой центрированной системы замкнутых в… … Математическая энциклопедия
БОРЕЛЯ — ЛЕБЕГА ТЕОРЕМА — о покрытии: пусть А ограниченнее замкнутое множество в Rn и G его открытое покрытие, т;, е: еистема открытых множеств, объединение к рых включает А; тогда существует конечная подсистема множеств , из G(подпокрытие), также являющаяся покрытием А … Математическая энциклопедия
МЕТРИЧЕСКОЕ ПРОСТРАНСТВО — множество Xвместе с нек рой метрикойr на ном. Теоретико множественный подход к изучению фигур (пространств) основан на исследовании взаимного расположения составляющих их элементарных частей. Одной из фундаментальных характеристик взаимного… … Математическая энциклопедия
Словарь терминов общей топологии — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И К Л М Н О П Р С Т У Ф Х Ц Ч … Википедия
Покрытие — У этого термина существуют и другие значения, см. Покрытие (значения). Покрытие в математике это семейство множеств, таких, что их объединение содержит заданное множество. Обычно понятие покрытия рассматривается в контексте общей топологии … Википедия

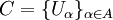 называется покрытием X, если
называется покрытием X, если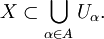
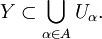
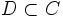 , также являющееся покрытием Y, называется подпокры́тием.
, также являющееся покрытием Y, называется подпокры́тием.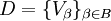 вписано в покрытие
вписано в покрытие 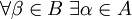 такое, что
такое, что 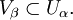
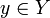 существует окрестность
существует окрестность 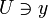 , пересекающаяся лишь с конечным числом элементов C, то есть множество
, пересекающаяся лишь с конечным числом элементов C, то есть множество 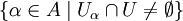 конечно.
конечно.