Как определить высоту недоступного объекта
Григорию Владимировичу понадобилось определить высоту дерева, находящегося на приусадебном участке. Дерево подверглось нападению жука типографа и его нужно срочно спилить. При этом нужно выбрать, в какую сторону оно должно упасть в результате спиливания, чтобы не повредить строения и насаждения на участке. Дерево было очень высокое, и он никак не мог найти возможность измерить его известными ему методами.
Ему на помощь пришла его дочь Ангелина, которая рассказала о том, что в курсе школьной программы они изучали тему «Подобие треугольников» и учитель объяснила всем ребятам, как можно измерить высоту предмета подручными средствами, с использованием знаний по математике и физике. Григорий Владимирович был очень удивлён, когда Ангелина сказала, что для проведения расчётов им понадобятся небольшое зеркало, рулетка и шнур.
Вооружившись всем необходимым, отец и дочь приступили к работе. Они проложили шнур от дерева по поверхности земли. На некотором удалении от дерева, на линии шнура, положили зеркало. После этого Ангелина встала на линии шнура так, чтобы верхушка дерева была ей видна в зеркале. «Папа, здесь «включается» физика: угол падения луча света равен углу отражения луча света.
Наличие двух равных углов в двух прямоугольных треугольниках позволяет говорить нам о подобии этих треугольников», – сказала Ангелина.
Затем Ангелина попросила отца произвести три замера:
-
расстояние от дерева до зеркала
-
расстояние от зеркала до того места, где стоит Ангелина
-
рост самой Ангелины.
Отец произвёл измерения. Расстояние от дерева до зеркала составило 10,3 м, от зеркала до Ангелины – 1,4 м, а рост Ангелины составил 1,65 м.
«А теперь, папа, всё очень просто! – воскликнула Ангелина. – Мне необходимо произвести несложные вычисления, и мы узнаем высоту нашего дерева».
В соответствии с построенным чертежом, Ангелина записала следующее:
AC = 1,4 м
CD = 10,3 м
AB = 1,65 м
KD = 1,65*10,3:1,4 = 12,139… м ≈ 12 м.
Высота треугольника | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU
Высота, проведенная в любом треугольнике, делит его на два прямоугольных треугольника, становясь смежным катетом. Сторона, на которую опущена высота, оказывается также разделенной на две пропорциональных части. Зная все три стороны, можно собрать их по теореме Пифагора, и приравняв высоту в качестве катета в двух вышеуказанных треугольниках, получить ее формулу для любого произвольного треугольника: 
С другой стороны, можно использовать сторону, прилежащую к высоте и угол α, чтобы вычислить высоту треугольника.
Известная его сторона будет гипотенузой в прямоугольном треугольнике, а сама высота – катетом, противолежащим углу α. Два этих измерения связывает синус угла, поэтому высота равна его произведению на сторону a: h=a sinα
Высота в прямоугольном треугольнике, опущенная из прямого угла (остальные две совпадают с катетами), получает особые свойства. Так как все три получившихся прямоугольных треугольника подобны друг другу, их стороны составляют пропорцию, которая раскладывается как квадрат высоты, равный произведению проекцию катетов на гипотенузу, или проще говоря, частей гипотенузы, на которые ее делит высота.
Из этого следует, что высота равна квадратному корню из данного произведения, а это есть не что иное как среднее пропорциональное приведенного выражения.
В равностороннем треугольнике, высота делит угол, из которого она исходит, на два одинаковых угла по 30°. Высота, оказываясь катетом, прилежащим к этому углу, внутри прямоугольного треугольника, подчиняется отношению косинуса угла α, а так как 
, а гипотенуза a, то формула высоты в равностороннем треугольнике будет выглядеть так: 
Как определить высоту объекта вблизи или на расстоянии? Рассказываю про 5 способов!
Как-то в юности я занимался альпинизмом и ориентированием на местности, и не знаю как сейчас, но в то время нужно было обязательно знать раздел «Выживание в экстремальных условиях», чтобы сдать экзамен и получить какой-либо разряд!
Собственно, решил поделиться с Вами и написать вкратце данную статью, полагая, что это будет очень познавательно и интересно! На самом деле способов еще гораздо больше, чем описано здесь, но они практически схожи, и вы в процессе чтения, вникнув в суть — сможете сами моделировать ситуации, и понять, что всё не так уж и сложно.
Ну что же, поехали…
Конечно не часто, но бывают в нашей жизни ситуации и обстоятельства, когда нужно знать высоту или расстояние до какого-либо объекта, например дома, дерева, да или похвастаться перед подругой))). Возможно придется строить траекторию для установки спутниковой тарелки, чтобы сигнал «стрелял» обходя высотки и не мешали кроны деревьев… ))) А мало ли, что еще…
Как ни парадоксально, но не забираясь с рулеткой на объект — расчет сделать не сложно, при том, что каждый метод может дать довольно точный результат. Конечно, с точностью до миллиметров не вычислить искомое значение, но погрешность будет точно уж небольшой.
Высота по отбрасываемой тени
Если погода солнечная и четко прослеживается тень, выбираем на объекте нижнюю контрольную точку от которой берет начало отбрасываемая тень будь-то дома, дерева, столба и пр.
После чего становимся сами или фиксируем в вертикальном положении любой предмет (на фото ниже — это обычный колышек) и аналогично замеряем длину его тени, а потом еще и высоту от точки начала тени до верхушки предмета. Иллюстрация — вычисление высоты
Надеюсь, что у вас нет сомнения, что на иллюстрации или фотографии данные треугольники подобны? Расчет строится на геометрическом свойстве подобных треугольников в которых отношения сторон равны и искомая высота объекта находится так:
для иллюстрации: Высота объекта Х = (x*Y) / y
Авторское фото — вычисление высоты столбадля фото: Высота столба = (Y2*X1) / X2
Угол падения — угол отражения
А если солнца нет и идет дождь, тоже не беда!
Согласно закону преломления из физики, о том что угол падения равен углу отражения — в зеркальном отражении любой лужи вы можете найти верхушку объекта и зная свой рост и расстояния соответственно, — получить искомую высоту (см.рисунок ниже).
Иллюстрация — ОтражениеЗафиксируйте точку О любым предметом, брошенным в лужу. Таким образом вы сможете измерить расстояния ОА, ОА1.
Зная все необходимые величины и основываясь на свойствах подобных треугольников, получите высоту, которая будет равна:
АВ = (А1В1 * ОА) / ОА1
Подручный предмет
Здесь требуется отойти от объекта и с помощью подручного предмета на вытянутой руке (ручки, карандаша, палки) замерить высоту. Конец предмета должен совпасть с верхней точкой объекта, а нижнюю точку требуется зафиксировать большим пальцем руки.
Иллюстрация — замер высотыРазверните предмет горизонтально так, чтобы низ его по-прежнему оставался у основания объекта, а кончик касался земли и указывал на определенную точку. Важно запомнить эту точку или, если есть помощник, попросить встать на эту точку. Как раз эта точка будет являться точкой проекции верхушки на землю и теперь остается только замерить расстояние.
Барометр и немного юмора
Нам понадобится немного знаний физики. Из школьного курса известно, что атмосферное давление зависит от высоты над уровнем моря и измерив давление у основания объекта и на вершине — можно вычислить расстояние подъема.
Средняя величина уменьшения атмосферного давления составляет 1 мм. рт. столба на каждые 12 м. высоты или 133,32 Па (Паскаль), что — то же самое. Поэтому, независимо от того, в каких единицах получено значение давления — вы всегда сможете посчитать высоту.
А если у вас есть секундомер (он есть в каждом телефоне), то сбросьте барометр с высоты, при этом засекая время его падения )))))). Путь, пройденный телом в свободном падении равен:
S = (g*t^2)/2, где:
g — ускорение свободного падения — 9.8 м./с^2;
t — время по секундомеру, с.
Определяем высоту объекта на расстоянии от вас
Для определения высоты нам в любом случае требуется расстояние до объекта, но основание его нам не доступно, — по-этому измерение нельзя произвести непосредственно.
Чтобы вычислить расстояние, нам нужно:
- Остановиться напротив объекта и зафиксировать эту точку (На рисунке точка А).
- Повернуться под прямым углом (на 90 град.) и сделать несколько шагов. Эта точка будет являться точкой О (здесь нужно воткнуть длинный предмет, например палку).
- Пройти то же расстояние, что и от А к О, и в том же направлении. Отметить каким-либо предметом (точка В).
- Повернуться под прямым углом (на 90 град.) и удаляться от объекта (в сторону точки Y) до тех пор, пока установленный ваш предмет в точке О не будет совмещен с объектом.
- Расстояние от вас (Y) до точки В — это и есть расстояние от точки А до объекта (Х).
Теперь, зная расстояние до объекта, переходим к вычислению его высоты.
Иллюстрация — вычисление высоты объектаДля простоты построения опять же подобных треугольников — берется шест с подвижной планкой (две доски сбиваются гвоздем). Устройство фиксируется в точке А, планка настраивается (при помощи врожденного глазомера в каждого из нас) на верхнюю точку объекта (Х1) — как показано на иллюстрации, после чего фиксируется.
Далее, отмечается на земле точка С.
В итоге мы получаем два треугольника СХХ1 и САА1, которые подобны между собой. Зная расстояние ХС, АС и АА1 находим искомую высоту Н объекта!
Высота Н = (АА1 * ХС) / АС.
Как определить высоту точек местности по топографической карте
Определение по топографической карте высот точек над уровнем моря (абсолютных высот) производится с помощью отметок на горизонталях. Если точка расположена на горизонтали, то задача сводится к определению отметки этой горизонтали. Если такой отметки на ней нет, то ее определяют по отметкам ближайших горизонталей или точек, высота которых обозначена на топографической карте.
Если точка находится между горизонталями, то для определения ее отметки надо установить направление ската, определить высоту ближайшей к ней нижней горизонтали. Затем прибавить к ней превышение данной точки. Оно определяется на глаз. Определение превышения одной точки над другой (относительное) определяется также с помощью отметок горизонталей.
Это надо знать при выборе наблюдательных пунктов, скрытых подступов, а также в случаях, когда необходимо установить, как просматривается местность с вероятных наблюдательных пунктов противника. Определение по топографической карте взаимной видимости сводится к тому, чтобы, не будучи на местности, установить, нет ли на направлении наблюдения какой-либо возвышенности или местного предмета, который будет перекрывать вашу линию видимости.
Определение видимости точек по топографической карте может быть выяснено наиболее просто и точно построением треугольника. Для этой цели соединяют на карте точки НП (наблюдательного пункта) и Ц (цели) прямой линией. Отмечают на этой линии точку возможного укрытия цели У. В конкретном примере это может быть высота с горизонталью 180.
Определив, какая из этих трех точек (НП, Ц, У) самая низкая, ставят около нее нуль. У остальных точек подписывают их превышение по отношению к этой нулевой точке. В нашем примере цель является нулевой точкой, укрытие выше ее на 15 метров, а наблюдатель на 25 метров.
Из точек, имеющих превышение над нулевой точкой, восстанавливают перпендикуляры к линии НП — Ц и откладывают на них (в произвольном, но в одинаковом масштабе) значение превышений (15 и 25). Затем прикладывают линейку к полученным точкам на перпендикулярах и проводят прямую линию (луч зрения).
Если эта прямая пройдет выше нулевой точки, то последняя видна не будет. В нашем примере цель не видна. Для того чтобы она была видна наблюдателю, надо подняться примерно на 5—6 метров — пунктирная линия на треугольнике.
Исходя из характеристики леса, допустим 20/0,3х5, известно, что высота деревьев — 20 метров, толщина стволов деревьев — 0,3 метра, а расстояние между ними — 5 метров. Полагая, что ствол каждого дерева имеет форму конуса, основанием которого служит круг диаметром 0,3 м3, а высота равна 20 метров. Этих данных вполне достаточно, чтобы вычислить объем дерева по известной формуле :
А чтобы узнать, сколько кубометров леса растет на одном гектаре, нужно определить общее количество деревьев на этой площади. Для нашего примера деревья отстоят друг от друга на 5 метров. Значит, на расстоянии 100 метров будет расположено 20 деревьев, а на площади 100х100 метров — 400. Объем древесины из такого леса на одном гектаре будет равен 0,47х400 = 188 м3.
Чтобы ответить на этот вопрос, надо знать среднюю скорость течения и поперечную площадь реки. Скорость течения реки указывается на карте, а поперечная площадь отсутствует. Но если воспользоваться шириной реки и ее глубиной и считать поперечную площадь ее — площадью треугольника или, более близкой к действительности, трапеции (нижнее основание ее равно половине ширины реки), то сравнительно просто можно подсчитать и секундный расход воды в реке.
Таковы те простейшие расчеты, которые можно выполнить по топографической карте, не выходя на местность. Но главная задача топографической карты все же сводится к изучению местности, изображенной на ней, и возможности ориентироваться на ней с помощью карты и компаса.
По материалам книги «Карта и компас — мои друзья».
Клименко А.И.
Статьи схожей тематики:
- Гирополукомпас, устройство, начальное ориентирование по ориентиру, магнитному азимуту, дирекционному углу, линии местности, выдерживание маршрута с помощью гирополукомпаса.
- Действия в пути при выдерживании маршрута движения на машинах по карте, восстановление ориентировки при сходе с маршрута движения.
- Особенности ориентирования при движении ночью, выбор ориентиров, изучение маршрута, особенности обеспечения боя при ведении наступления ночью.
- Определение севера и сторон горизонта по тени шеста, по часам и по звездам ночью в Северном и Южном полушариях.
- Ориентирование по карте в движении, склеивание листов и складывание карты, подъем маршрута, выбор ориентиров, определение протяженности маршрута и азимутов.
- Аэрофотосъемка, аэроснимки местности, виды воздушного фотографирования и аэроснимков местности.
1.2. Определение по карте высот и
взаимного превышения точек местности
Высоты точек местности над уровнем моря (абсолютные высоты) определяют по карте с помощью отметок высот горизонталей и принятой на карте высоты сечения рельефа.
Если точка расположена на горизонтали, то ее абсолютная высота равна значению отметки этой горизонтали. Например, на рис. 6 горизонталь с отметкой 200 проходит через сарай. Это значит, что сарай расположен на высоте 200 м над уровнем моря.
В случае, когда горизонталь не имеет подписанной отметки, ее значение определяют по отметкам других горизонталей или высот точек местности. Допустим, требуется определить высоту точки местности, на которой находиться отдельный камень (рис. 6). Условный знак отдельного камня (1,3) расположен на горизонтали без отметки. Штрихи (указатели скатов) на горизонталях показывают, что скат понижается в сторону озера (Глубокое). Слева от горизонтали с отдельным камнем находится утолщенная горизонталь с отметкой 200. Высота сечения равна 10 м. Значит горизонталь проходящая через условный знак отдельного камня, имеет отметку 190, которая является высотой точки.
Если точка находится между горизонталями, то ее абсолютная высота определяется по значению отметки высоты одной из этих горизонталей. Для этого значению отметки высоты горизонтали добавляют или из нее вычитают (в зависимости от положения точки относительно горизонтали) ту часть высоты сечения, на которую точка удалена от горизонтали.
Например, нужно определить высоту развилки полевых дорог (рис. 6, точка В). Точка расположена примерно на 3/4 выше значения заложения от нижней горизонтали, имеющей отметку 220, и на 1/4 ниже – от верхней горизонтали с отметкой 230. Высота сечения рельефа 10 м. Следовательно, поправка к нижней горизонтали (220 м) составит 7,5 м, а к верхней горизонтали (230 м) – 2,5 м. Прибавляя поправку к значению отметки нижней горизонтали или вычитая ее из значения отметки верхней горизонтали, получим высоту точки на развилке дорог: 220 м + 7,5 м = 227,5 около 227 м. или 230 м – 2,5 м = 227,5 около 227 м. |
|
Рис. 6. Определение высоты и взаимного превышения точек по карте |
Взаимное превышение точек местности определяется как разность его абсолютных высот. Например, превышение высоты с отметкой 236,3 (рис. 6) над оз. Глубокое (с отметкой 177,8) составляет:
236,3-177,8=58,5 м
Относительные высоты скатов вершин и глубины лощин удобно определять по числу промежутков между горизонталями на них. Подсчитав число промежутков между горизонталями на скате и умножив его на высоту сечения, получим относительную высоту ската. Например, на юго-западном скате высоты с отметкой 236,3 (рис. 16) имеются три промежутка между основными горизонталями и один между основной и дополнительной горизонталями. Высота сечения 10 м, поэтому относительная высота ската будет 3,5 х 10 м=35 м.
Относительные высоты (глубины) обрывов, оврагов, насыпей, выемок определяются с помощью подписей, стоящих рядом с условными знаками.
Определение по карте направления понижения и крутизны скатов. Направление понижения скатов определяется на карте по указателям скатов на горизонталях, а также путём сравнения отметок высот точек и горизонталей: понижение ската будет всегда в сторону меньшей отметки; цифры отметок горизонталей своими основаниями направлены в сторону понижения ската.
Крутизна ската определяется по значению заложения: чем меньше значение заложения, тем скат круче. На топографических картах масштаба 1:25 000, 1:50 000 и 1:100 000 основная высота сечения рельефа подобрана таким образом, что заложения между основными горизонталями в 1 см соответствует крутизна ската 1,2º (округленно до 1º).
Из этой зависимости между заложением, высотой сечения и крутизной ската можно вывести следующее правило: во сколько раз заложение меньше (больше) 1 см, во столько раз крутизна ската больше (меньше) 1º. Отсюда следует, что заложению в 1 мм соответствует крутизна ската 12º (округленно 10º), заложению в 2 мм – 6º (округлено до 5º), заложению в 5 мм – 2,4º (округлено до 2º) и т.д.
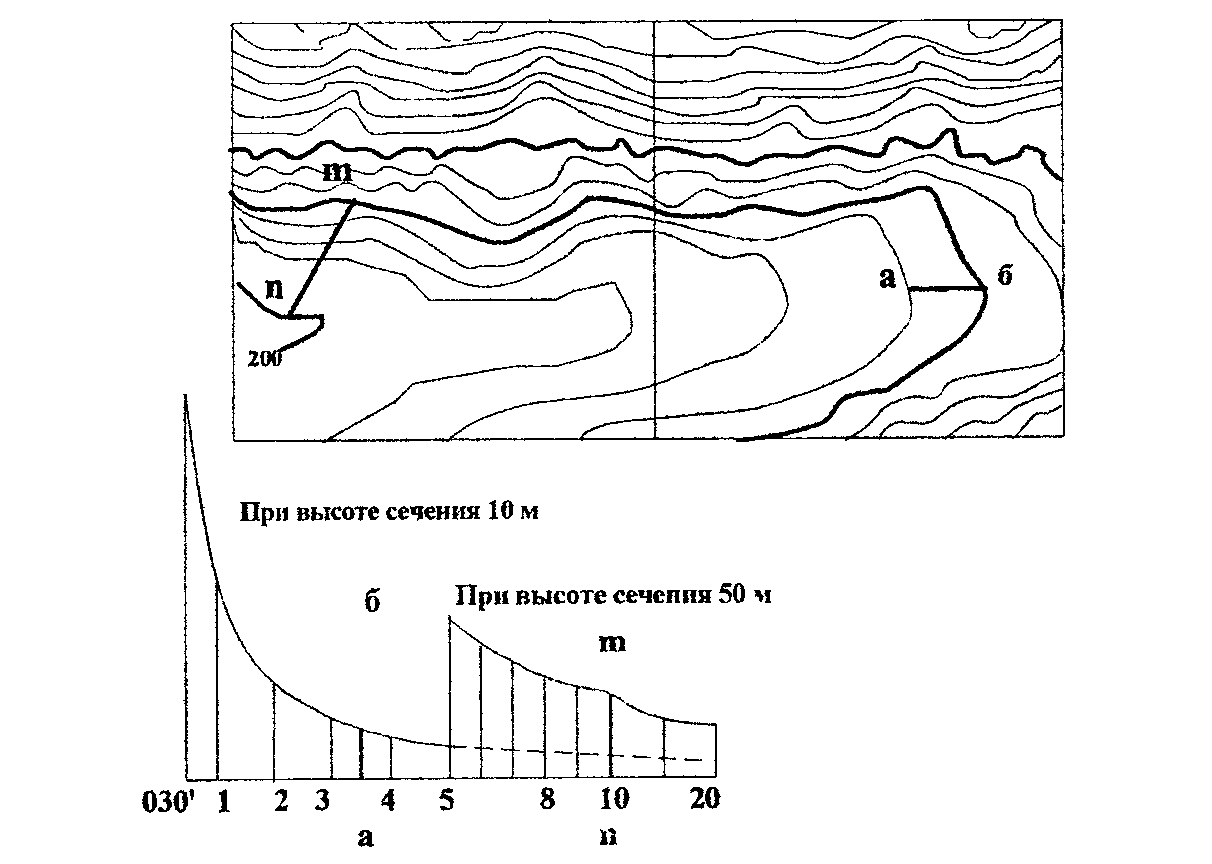
Более точно крутизна ската может быть определена при помощи специального графика, называемого шкалой заложений (рис. 7), которая располагается под южной стороной рамки карты. Вдоль горизонтального основания шкалы подписаны цифры, обозначающие крутизну скатов в градусах. На перпендикулярах к основанию отложены соответствующие им заложения. |
|
Рис. 7. Определение крутизны скатов по шкале заложений |
Шкала заложений дается для двух высот сечений: одна – для заложений между основными горизонталями, другая – для заложений между утолщенными горизонталями.
Для определения крутизны скатов по шкале заложений следует измерить расстояние между двумя смежными сплошными горизонталями в нужном направлении и отложить его на шкале заложений так, как показано на рис. 7. Отсчет внизу на шкале против отложенного отрезка укажет крутизну ската в градусах.
В нашем примере крутизна ската между точками а и б равна 3,5º. На крутых скатах, где горизонтали проходят близко одна от другой, крутизну удобнее определять по утолщенным горизонталям. Для этого измеряют отрезок между соседними утолщенными горизонталями, отложив его на правой части шкалы, как показано на рис. 7, и определяют крутизну ската. В нашем примере крутизна ската между точками n и m равна 10º.
Геодезическая высота — Википедия
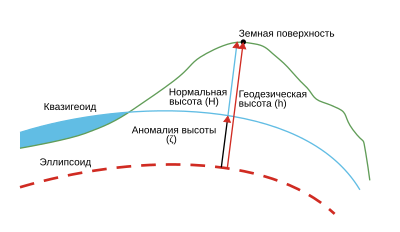Разница между нормальной, геодезической и высотой квазигеоидаГеодези́ческой (эллипсоида́льной) высото́й некоторой точки физической поверхности земли называется отрезок нормали к эллипсоиду от его поверхности до данной точки. Вместе с геодезическими широтой и долготой (B и L соответственно) она определяет положение точки относительно заданного эллипсоида. Физически эллипсоида не существует, следовательно геодезическая высота не может быть непосредственно измерена наземными методами. Определить её возможно с помощью спутниковых измерений, а также посредством обработки рядов триангуляции, астрономо-геодезического нивелирования.
Как видно из определения геодезическая высота зависит от расположения и параметров выбранного эллипсоида, поэтому геодезическую высоту разделяют на две части. Одна из них характеризует физическую поверхность Земли относительно уровенной поверхности (информацию о ней получают в большей степени нивелированием), вторая, более гладкая, характеризует отличие отсчётного эллипсоида от геоида. Первую часть называют гипсометрической, а вторую — гладкой или геоидальной частью. Уровенная поверхность имеет несравненно более плавную форму в сравнении с физической, следовательно геоидальная часть меняется гораздо медленнее гипсометрической.
В зависимости от особенностей выбора гипсометрической части существуют разные системы геодезических высот:
Ортометрическая система высот[править | править код]
Ортометрическая высота точки — это расстояние (H) вдоль отвесной линии от точки до поверхности Геоида. Ортометрическая высота для практических целей является «высотой над уровнем моря».
Ортометрическая система высот как правило привязанна к определенной высоте в одной точке, а не к точному среднему уровню моря в любом месте.
Ортометрические высоты обычно используются для инженерных работ, хотя и динамическая высота может быть использованна для крупномасштабных гидрологических целей.
Альтернативой ортометрической высоте являются динамическая высота и нормальная высота.
Различные страны используют различные исходные точки опорной поверхности. В России исходным считается Кронштадтский футшток и Балтийская система высот. В США текущий датум NAVD88.
Поскольку гравитация не является постоянной на больших площадях, ортометрическая высота также не является постоянной. Так на территории США гравитация на 0,1% сильнее на севере Соединенных Штатов, чем на юге, поэтому ровная поверхность, имеющая ортометрическую высоту в 1000 метров в Монтане, будет иметь высоту в 1001 метр в Техасе.
Нормальная система высот[править | править код]
Нормальные высоты — это высоты от поверхности квазигеоида, один из нескольких типов высоты. Альтернативы: ортометрическая высота и динамические высоты.
Нормальная высота точки вычисляется из геопотенциальных чисел путем деления геопотенциального числа точки, т. е. ее разности геопотенциалов с уровнем моря, на среднюю нормальную гравитацию, вычисленную вдоль отвеса точки. (Точнее, вдоль эллипсоидной нормали, усредняя по диапазону высот от 0-эллипсоид-H*; процедура, таким образом, рекурсивна.
Нормальные высоты, таким образом, зависят от выбранного опорного эллипсоида. Советский Союз и многие другие страны Восточной Европы выбрали высотную систему, основанную на нормальных высотах, определяемых геодезическим точным нивелированием.
Нормальные значения гравитации легко вычислить через плотность земной коры вокруг отвеса.
Нормальные высоты занимают видное место в теории гравитационного поля Земли, разработанной школой М. С. Молоденского.
Эталонная поверхность, с которой измеряются нормальные высоты, называется квазигеоидом, представляющим собой «средний уровень моря», аналогичный геоиду и близкий к нему, но лишенный физической интерпретации эквипотенциальной поверхности.
Динамическая система высот[править | править код]
Динамическая высота — это относительный способ указания высоты точки отличной от исходного футштока (глобальной системы высот), в отличие от ортометрической высоты или нормальной высоты. Т.е динамическая высота является локальной.
Динамическая высота является наиболее подходящей мерой высоты при работе с уровненными поверхностями на большой географической территории и используется Датумом Великих Озер в США и Канаде.
Динамическая высота постоянна, если следовать одному и тому же гравитационному потенциалу, когда они перемещаются с места на место. Из-за изменения силы тяжести поверхности, имеющие постоянную разницу в динамической высоте, могут быть ближе или дальше друг от друга в различных местах. Динамические высоты обычно выбираются так, чтобы они имели сопряжения с геоидом.
Когда оптическое выравнивание выполнено, путь близко соответствует следующему значению динамической высоты по горизонтали, но не ортометрической высоте для вертикальных изменений, измеренных на выравнивающем стержне. Таким образом, небольшие поправки должны быть применены к полевым измерениям, чтобы получить либо динамическую высоту, либо ортометрическую высоту, обычно используемую в технике. Паспорта данных Национальной Геодезической службы США дают как динамические, так и ортометрические значения.
Динамическая высота может быть вычислена с использованием нормальной силы тяжести на 45-градусной широте и геопотенциального числа местоположений.
- Огородова Л. В. Часть 3. Теоретическая геодезия. // «Высшая геодезия». Учебник для вузов. — Москва: Геодезиздат, 2006. — 384 с. — ISBN 5-86066-076-6.
% способов определения высоты предметов
Определение высоты некоторых предметов
Рекомендуем несколько способов, при помощи которых можно определить высоту предметов.
1. По тени. В солнечный день можно определить высоту предмета по его тени, руководствуясь следующим правилом: высота измеряемого предмета во столько раз больше высоты известного вам предмета (палки, удочки), во сколько раз тень от измеряемого предмета больше тени от палки, удоччки.
Если при измерении окажется, что тень от палки или удочки в 2 раза больше длины палки или удочки, то высота измеряемого предмета будет в 2 раза меньше длины его тени, а если тень от палки или удочки будет равна их длине, высота измеряемого предмета также равна высоте своей тени.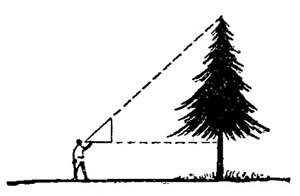
2. При помощи равнобедренного треугольника. Приближаясь к предмету (например, к дереву) или удаляясь от него, установить треугольник у глаза так, чтобы один из его катетов был направлен отвесно, а другой совпал с линией визирования на вершину дерева. Высота дерева будет равняться расстоянию до дерева (в шагах) плюс высота до глаз наблюдателя.
3. По шесту. Взять шест, равный своему росту, и установить его на таком расстоянии от предмета (дерева), чтобы лёжа можно было видеть верхушку дерева на одной прямой с верхней точкой шеста.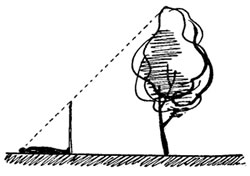
Высота дерева будет равна расстоянию от головы наблюдателя до основания дерева.
4. При помощи высотомера со стрелкой. Изготовив прибор по данному чертежу, можно приступить к определению высоты какого-либо предмета. Находясь на различном расстоянии от предмета, надо следить, чтобы при визировании вершины дерева показания стрелки не выходили за пределы шкалы.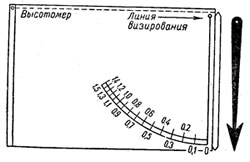
При визировании следует приложить глаз к отверстию сбоку прибора и, наклонив прибор, добиться, чтобы вторая визирная точка (угол на другом конце прибора) совпала с вершиной визируемого предмета. Стрелка укажет число, на которое следует умножить расстояние до предмета, чтобы получить его высоту. К этому прибавляется выста прибора во время визирования.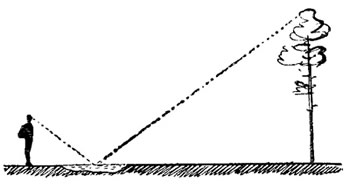
5. При помощи лужи. Если недалеко от дерева находится лужа, надо стать так, чтобы она помещалась между вами и предметом, а затем при помощи горизонтально положенного зеркальца найти в воде отражение вершины деерва. Высота дерева будет во столько раз больше роста человека, во сколько раз расстояние от него до лужи больше, чем расстояние от лужи до наблюдателя.