Найти прямой угол: Как сделать прямой угол между стенами – Прямой угол — Википедия

Прямой угол | Треугольники

Чему равен прямой угол? Как изобразить прямой угол? Как найти  прямые углы на рисунке?

Прямой угол — это угол, градусная мера которого равна 90º.

I. Проще всего изобразить прямой угол по клеточкам.

1) Точку — вершину прямого угла — ставим на пересечении клеточек.

2) Из вершины проводим лучи — стороны угла: один — горизонтально, другой — вертикально.

3) Ставим знак прямого угла — маленький квадрат при вершине: □

∠ABC=90º,

то есть угол ABC — прямой.

 

II. Другой способ построения прямого угла — при помощи транспортира:

1) Отмечаем точку — вершину угла.

2) От вершины проводим луч — сторону угла.

3) Совмещаем вершину угла с отметкой в центре транспортира (у разных моделей положение отметки может быть различным) так, чтобы отметка 0º располагалась на стороне угла.

4) На отметке 90 градусов ставим точку.

5) От вершины через эту точку проводим второй луч — другую сторону угла:

III. Ещё один способ построения прямого угла — с помощью угольника.

1) Отмечаем точку — вершину угла.

1) От вершины угла проводим луч — первую сторону угла.

2) Прикладываем угольник прямым углом к вершине угла так, чтобы одна сторона угольника проходила через первую сторону угла.

3) Вдоль другой стороны угольника проводим другой луч — вторую сторону угла.

Чтобы по рисунку найти прямой угол, также можно использовать угольник.

Если приложить угольник к вершине угла вдоль одной из сторон, то  в остром угле вторую сторону угольник частично закроет (так как градусная мера острого угла меньше 90º), в тупом — вторая сторона окажется за угольником (поскольку тупой угол больше 90º), и только в прямом угле другая сторона угольника пройдёт ровно вдоль второй  стороны:

Треугольник, один из углов которого — прямой, называется прямоугольным.

Угол между пересекающимися прямыми: определение, примеры нахождения

Данный материал посвящен такому понятию, как угол между двумя пересекающимися прямыми. В первом пункте мы поясним, что он из себя представляет, и покажем его на иллюстрациях. Потом разберем, какими способами можно найти синус, косинус этого угла и сам угол (отдельно рассмотрим случаи с плоскостью и трехмерным пространством), приведем нужные формулы и покажем на примерах, как именно они применяются на практике.

Что такое угол между пересекающимися прямыми

Для того чтобы понять, что такое угол, образующийся при пересечении двух прямых, нам потребуется вспомнить само определение угла, перпендикулярности и точки пересечения.

Определение 1

Мы называем две прямые пересекающимися, если у них есть одна общая точка. Эта точка называется точкой пересечения двух прямых.

Каждая прямая разделяется точкой пересечения на лучи. Обе прямые при этом образуют 4 угла, из которых два – вертикальные, а два – смежные. Если мы знаем меру одного из них, то можем определить и другие оставшиеся.

Допустим, нам известно, что один из углов равен α. В таком случае угол, который является вертикальным по отношению к нему, тоже будет равен α. Чтобы найти оставшиеся углы, нам надо вычислить разность 180°-α. Если α будет равно 90 градусам, то все углы будут прямыми. Пересекающиеся под прямым углом линии называются перпендикулярными (понятию перпендикулярности посвящена отдельная статья).

Взгляните на рисунок:

Перейдем к формулированию основного определения.

Определение 2

Угол, образованный двумя пересекающимися прямыми – это мера меньшего из 4-х углов, которые образуют две эти прямые.

Из определения нужно сделать важный вывод: размер угла в этом случае будет выражен любым действительным числом в интервале (0, 90]. Если прямые являются перпендикулярными, то угол между ними в любом случае будет равен 90 градусам.

Как найти угол между пересекающимися прямыми на плоскости

Умение находить меру угла между двумя пересекающимися прямыми полезно для решения многих практических задач. Метод решения можно выбрать из нескольких вариантов.

Для начала мы можем взять геометрические методы. Если нам известно что-то о дополнительны

как найти прямой угол при разметке земли под теплицу

По сути то же можно проделать рулеткой. Берете одну сторону, например 4м и из ее концов проводите дуги радиусом 3м и 5 м. Точка пересечения — угол прямоугольного треугольника.

Согласен с Андреем… редко когда прибегали при разметке простейших объектов к теодолиту.. . Обычно при помощи теоремы Пифагора и двух рулеток отмеряли прямой угол. 3м и 4м катеты и 5м гипотенуза. Сперва откладуешь один катет, забивая колы (к примеру 3м) в нужном направлении, затем от колов соединяешь две рулетки: на одной 4м должно совпадать с 5м другой.. . или методом «циркуля», как описал Андрей. так что школьных знаний геометрии вполне достаточно для таких простых вещей.

Все гениальное просто.

без всяких теорем! меряешь рулеткой, делаешь одинаковые диагонали и все! в прямоугольнике с одинаковыми диагонали будут углы 90 град. иначе быть н может!

Жаль, не умею пока здесь рисовать. Из построения угла в школьной геометрии. Проводите длинную линию, по углам вставьте палки, к каждой — веревку длины больше половины линии привяжите, к свободному концу палки другую палочку, и как циркулем делаете на земле дугу с каждой стороны до пересечения дуг. Соединяете пересечение с серединой нарисованной линии. вот Вам и два прямых угла. В вашем конкретном случае чтобы угол получился где надо, от угла будущей теплицы проведите прямую по обе его стороны на равном расстоянии в направлении будущей ее стены. Успеха!

Да че заморачиваться, у прямоугольника диагонали должны быть равны- от этого и пляшите, бечевка, колышки-вот Вам идеальные углы и стороны.

Одна сторона 80, другая 60, между ними метр, соответственно увеличиваешь стороны в 2 раза получаешь 2м….

теорема пифагора: квадрат гипотеузы (диагональ) равен сумме квадратов катета (длина и ширина теплицы)

Угол между прямыми

Определение угла между прямыми

Две прямые называются пересекающимися, если они имеют единственную общую точку. Эта точка называется точкой пересечения прямых. Прямые разбиваются точкой пересечения на лучи, которые образуют четыре неразвернутых угла, среди которых две пары вертикальных углов и четыре пары смежных углов. Если известен размер одного из углов, образованных пересекающимися прямыми, то легко определить размер остальных углов. Если один из углов прямой, то все остальные тоже прямые, а прямые перпендикулярны.

Определение Угол между прямыми — размер наименьшего из углов, образованных этими прямыми.

Угол между прямыми на плоскости

Угол между прямыми заданными уравнениями с угловым коэффициентом

Если две прямые заданы уравнениями с угловым коэффициентом

y = k₁x + b₁,
y = k₂x + b₂,

то угол между ними можно найти, используя формулу:

tg γ = k₁ — k₂1 + k₁·k₂

Если знаменатель равен нулю (1 + k₁·k₂ = 0), то прямые перпендикулярны.

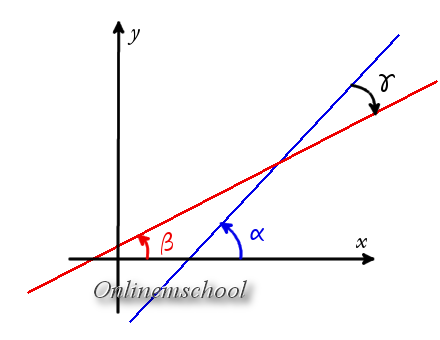Доказательство. Если прямые заданы уравнениями с угловыми коэффициентами, то легко найти углы между этими прямыми и осью OX

tg α = k₁
tg β = k₂

Соответственно легко найти угол между прямыми

γ = α — β

tg γ = tg (α — β) = tg α — tg β1 + tg α ·tg β = k₁ — k₂1 + k₁·k₂

Угол между прямыми через направляющие векторы этих прямых

Если a — направляющий вектор первой прямой и b — направляющий вектор второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:

cos φ = |a · b||a| · |b|

Если уравнение прямой задано параметрически

x = l t + ay = m t + b

то вектор направляющей имеет вид {l; m}

Если уравнение прямой задано как

A x + B y + C = 0

то для вычисления направляющего вектора, можно взять две точки на прямой.
Например, если C ≠ 0, A ≠ 0, C ≠ 0 , при x = 0 => y = -CB значит точка на прямой имеет координаты K(0, -CB), при y = 0 => x = -CA значит точка на прямой имеет координаты M(-CA, 0). Вектор направляющей KM = {-CA; CB}.

Если дано каноническое уравнение прямой

x — x₀l = y — y₀m

то вектор направляющей имеет вид {l; m}

Если задано уравнение прямой с угловым коэффициентом

y = kx + b

то для вычисления направляющего вектора, можно взять две точки на прямой, например, при x = 0 => y = b значит точка на прямой имеет координаты K(0, b), при x = 1 => y = k + b значит точка на прямой имеет координаты M(1, k + b). Вектор направляющей KM = {1; k}

Угол между прямыми через векторы нормалей этих прямых

Если a — вектор нормали первой прямой и b — вектор нормали второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:

cos φ = |a · b||a| · |b|

Если уравнение прямой задано как

A x + B y + C = 0

то вектор нормали имеет вид {A; B}

Если задано уравнение прямой с угловым коэффициентом

y = kx + b

то вектор нормали имеет вид {1; -k}

Угол между прямыми через направляющий вектор и вектор нормали этих прямых

Если a — направляющий вектор первой прямой и b — вектор нормали второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:

sin φ = |a · b||a| · |b|

Примеры задач на вычисления угла между прямыми на плоскости

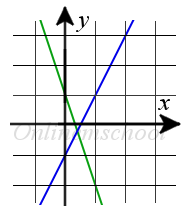Пример 1. Найти угол между прямыми y = 2x — 1 и y = -3x + 1.

Решение: Воспользуемся формулой для вычисления угла между прямыми заданными уравнениями с угловым коэффициентом:

tg γ = k₁ — k₂1 + k₁·k₂ = 2 — (-3)1 + 2·(-3) = 5-5 = 1

Ответ. γ = 45°

Пример 2. Найти угол между прямыми y = 2x — 1 и x = 2t + 1y = t.

Решение: Воспользуемся формулой для вычисления угла между прямыми у которых известны направляющие векторы.

Для первой прямой направляющий вектор {1; 2}, для второй прямой направляющий вектор {2; 1}

cos φ = |1 · 2 + 2 · 1|1² + 2² · 2² + 1² = 45 · 5 = 0.8

Ответ. φ ≈ 36.87°

Пример 3 Найти угол между прямыми 2x + 3y = 0 и x — 23 = y4.

Решение: Для решения этой задачи можно найти направляющие векторы и вычислить угол через направляющие векторы или преобразовать уравнения в уравнения с угловым коэффициентом и вычислить угол через угловые коэффициенты.

Преобразуем имеющиеся уравнения в уравнения с угловым коэффициентом.

2x + 3y = 0 => y = -23x   (k₁ = -23)

x — 23 = y4 => y = 43x — 83   (k₂ = 43)

tg γ = k₁ — k₂1 + k₁·k₂ = -23 — 431 + (-23)·43 = -631 — 89 = 18

Ответ. γ ≈ 86.82°

Угол между прямыми в пространстве

Если a — направляющий вектор первой прямой, а b — направляющий вектор второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:

cos φ = |a · b||a| · |b|

Если дано каноническое уравнение прямой

x — x₀l = y — y₀m = z — z₀n

то направляющий вектор имеет вид {l; m; n}

Если уравнение прямой задано параметрически

x = l t + ay = m t + bz = n t + c

то направляющий вектор имеет вид {l; m; n}

Пример 4. Найти угол между прямыми x = 2t + 1y = tz = -t — 1 и x = t + 2y = -2t + 1z = 1.

Решение: Так как прямые заданы параметрически, то {2; 1; -1} — направляющий вектор первой прямой, {1; -2; 0} направляющий вектор второй прямой.

cos φ = |2 · 1 + 1 · (-2) + (-1) · 0|2² + 1² + (-1)² · 1² + (-2)² + 0² = 06 · 5 = 0

Ответ. φ = 90°

Пример 5 Найти угол между прямыми x — 23 = y4 = z — 35 и -x — 22 = 1 — 3y = 3z — 52.

Решение: Для решения этой задачи найдем направляющие векторы этих прямых.

Уравнение первой прямой задано в канонической форме, поэтому направляющий вектор {3; 4; 5}.

Преобразуем второе уравнение к каноническому вид.

-x — 22 = x — 2-2

1 — 3y = 1 + y-1/3 = y — 1/3-1/3

3z — 52 = z — 5/32/3

Получено уравнение второй прямой в канонической форме

x — 2-2 = y — 1/3-1/3 = z — 5/32/3

{-2; -13; 23} — направляющий вектор второй прямой.

cos φ = 3·(-2) + 4·(-13) + 5·233² + 4² + 5² · (-2)² + (-13)² + (23)² = -6 — 43 + 1039 + 16 + 25 · 4 + 19 + 49 = -450 · 41/9 = 12582 = 682205

Ответ. φ ≈ 74.63°

Угол между прямыми онлайн

С помощью этого онлайн калькулятора можно найти угол между прямыми. Дается подробное решение с пояснениями. Для вычисления угла между прямыми, задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), введите элементы уравнения в ячейки и нажимайте на кнопку «Решить». Теоретическую часть смотрите ниже.

Очистить все ячейки?

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

 

1. Угол между прямыми на плоскости

Прямые заданы каноническими уравнениями

1.1. Определение угла между прямыми

Пусть в двухмерном пространстве прямые L₁ и L₂ заданы каноническими уравнениями

и

где q₁=(m₁, p₁) направляющий вектор прямой L₁, а q₂=(m₂, p₂) направляющий вектор прямой L₂.

Задача об определении угла между прямыми L₁ и L₂ сводится к задаче об определении угла между направляющими векторами q₁ и q₂ (рис.1).

Из определения скалярного произведения:

где |q₁| и |q₂| модули направляющих векторов q₁ и q₂ соответственно, φ -угол между векторами q₁ и q₂.

Из выражения (1.3) получим:

Таким образом, из формулы (1.4) можно найти угол между прямыми L₁ и L₂. Как видно из Рис.1 пересекающиеся прямые образуют смежные углы φ и φ₁. Если найденный угол больше 90°, то можно найти минимальный угол между прямыми L₁ и L₂: φ₁=180-φ.

Из формулы (1.4) можно вывести условия параллельности и перпендикулярности двух прямых.

Пример 1. Определить угол между прямыми

и

Решение. Прямая (1.5) имеет направляющий вектор q₁=(m₁, p₁)=(3, 4), а прямая (1.6) − q₂=(m₂, p₂)=(− 3, 1). Для определения угла между прямыми (1.5) и (1.6) подставим значения m₁, p₁, m₂, p₂ в (1.4):

Упростим и решим:

Найдем угол φ

Данный угол больше 90°. Найдем минимальный угол между прямыми. Для этого вычтем этот угол из 180:

Ответ.

Угол между прямыми равен:

1.2. Условие параллельности прямых

Пусть φ=0. Тогда cosφ=1. При этом выражение (1.4) примет следующий вид:

Сделаем преобразования с выражением (1.7):

Таким образом условие параллельности прямых L₁ и L₂ имеет вид (1.8). Если m₂≠0 и p₂≠0, то (1.8) можно записать так:

Пример 2. Определить, параллельны ли прямые

и

Решение. Прямая (1.10) имеет направляющий вектор q₁=(m₁, p₁)=(3, 3), а прямая (1.11) − q₂=(m₂, p₂)=(−2, −2). Тогда

Удовлетворяется равенство (1.9), следовательно прямые (1.10) и (1.11) параллельны.

Ответ. Прямые (1.10) и (1.11) параллельны.

1.3. Условие перпендикулярности прямых

Пусть φ=90°. Тогда cosφ=0. При этом выражение (1.4) примет следующий вид:

Правая часть выражения (1.12) равно нулю тогда и только тогда, когда числитель равен нулю. Следовательно, для того, чтобы прямые L₁ и L₂ были перпендикулярны , должно выполняться условие

Пример 3. Определить, перпендикулярны ли прямые

и

Решение. Прямая (1.14) имеет направляющий вектор q₁=(m₁, p₁)=(3, 1), а прямая (1.15) − q₂=(m₂, p₂)=(−2, 6). Тогда

Удовлетворяется условие (1.13), следовательно прямые (1.14) и (1.15) перпендикулярны.

Ответ. Прямые (1.14) и (1.15) перпендикулярны.

Прямые заданы общими уравнениями

1.4. Определение угла между прямыми

Пусть две прямые L₁ и L₂ заданы общими уравнениями

и

Так как нормальным вектором прямой L₁ является n₁=(A₁, B₁), а нормальным вектором прямой L₂ является n₂=(A₂, B₂), то задача об определении угла между прямыми L₁ и L₂ сводится к определению угла φ между векторами n₁ и n₂ (Рис.2).

Из определения скалярного произведения двух векторов, имеем:

где |n₁| и |n₂| модули нормальных векторов n₁ и n₂ соответственно, φ -угол между векторами n₁ и n₂.

Из уравнения (19) получим

Пример 4. Найти угол между прямыми

и

Решение. Прямая (1.21) имеет нормальный вектор n₁=(A₁, B₁)=(5, −2), а прямая (1.22) − n₂=(A₂, B₂)=(1, 3). Задача определения угла между прямыми L₁ и L₂ сводится к определению угла между векторами n₁ и n₂. Из определения скалярного произведения векторов имеем: (n₁,n₂)=|n₁||n₂|cosφ. Тогда

Подставляя значения A₁, B₁, A₂, B₂ в (1.23), получим:

Упростим и решим:

Найдем угол φ:

Данный угол больше 90°. Найдем минимальный угол между прямыми. Для этого вычтем этот угол из 180:

1.5. Условие параллельности прямых

Так как угол между паралленьными прямыми равен нулю, то φ=0, cos(φ)=1. Тогда сделав преобразования, представленные выше для канонических уравнений прямых получим условие параллельности:

С другой стороны условие параллельности прямых L₁ и L₂ эквивалентно условию коллинеарности векторов n₁ и n₂ и можно представить так:

Как видим уравнения (1.24) и (1.25) эквивалентны при A₂≠0 и B₂≠0. Если в координатах нормальных векторов существует нулевой коэффициент, то нужно использовать уравнение (1.24).

Пример 5. Определить, параллельны ли прямые

и

Решение. Прямая (1.26) имеет нормальный вектор n₁=(A₁, B₁)=(4, 2), а прямая (1.27) − n₂=(A₂, B₂)=(2, 1). Тогда подставляя значения A₁, B₁, A₂, B₂ в (1.24), получим

Удовлетворяется равенство (1.24), следовательно прямые (1.26) и (1.27) параллельны.

Ответ. Прямые (1.26) и (1.27) параллельны.

1.6. Условие перпендикулярности прямых

Условие перпендикулярности прямых L₁ и L₂ можно извлекать из формулы (1.20), подставляя cos(φ)=0. Тогда скалярное произведение (n₁,n₂)=0. Откуда

Таким образом условие перпендикулярности прямых определяется равенством (1.28).

Пример 6. Определить, перпендикулярны ли прямые

и

Решение. Прямая (1.29) имеет нормальный вектор n₁=(A₁, B₁)=(4, −1), а прямая (1.30) − n₂=(A₂, B₂)=(2, 8). Тогда подставляя значения A₁, B₁, A₂, B₂ в (28), получим

Удовлетворяется равенство (1.28), следовательно прямые (1.29) и (1.30) перпендикулярны.

Ответ. Прямые (1.29) и (1.30) перпендикулярны.

2. Угол между прямыми в пространстве

2.1. Определение угла между прямыми

Пусть в пространстве прямые L₁ и L₂ заданы каноническими уравнениями

и

где q₁=(m₁, p₁, l₁) направляющий вектор прямой L₁, а q₂=(m₂, p₂, l₂) направляющий вектор прямой L₂.

Задача об определении угла между прямыми L₁ и L₂ сводится к задаче об определении угла между направляющими векторами q₁ и q₂ .

Из определения скалярного произведения:

где |q₁| и |q₂| модули направляющих векторов q₁ и q₂ соответственно, φ -угол между векторами q₁ и q₂.

Из выражения (2.3) получим:

Таким образом, из формулы (2.4) можно найти угол между прямыми L₁ и L₂. Если найденный угол больше 90°, то можно найти минимальный угол между прямыми L₁ и L₂: φ₁=180-φ.

Из формулы (2.4) можно вывести условия параллельности и перпендикулярности двух прямых.

Пример 1. Определить угол между прямыми

и

Решение. Прямая (2.5) имеет направляющий вектор q₁=(m₁, p₁, l₁)=(1, 1, 3), а прямая (2.6) − q₂=(m₂, p₂, l₂)=(− 3, 1, 2). Для определения угла между прямыми (2.5) и (2.6) подставим значения m₁, p₁, l₁, m₂, p₂, l₂ в (2.4):

Упростим и решим:

Найдем угол φ

Ответ.

Угол между прямыми равен:

2.2. Условие параллельности прямых

Условие параллельности прямых эквивалентно условию коллинеарности направляющих векторов q₁ и q₂, т.е. соответствующие координаты этих векторов пропорциональны. Пусть

где α − некоторое число. Тогда соответствующие координаты векторов q₁ и q₂ пропорциональны, и, следовательно прямые L₁ и L₂ параллельны.

Условие параллельности прямых можно представить и так:

Отметим, что любую пропорцию нужно понимать как равенство ad=bc.

Пример 2. Определить, параллельны ли прямые

и

Решение. Прямая (2.9) имеет направляющий вектор q₁=(m₁, p₁, l₁)=(3, 2, 4), а прямая (2.10) − q₂=(m₂, p₂, l₂)=(6, 4, 8). Тогда

Удовлетворяется равенство (2.8) (или (2.7)), следовательно прямые (2.9) и (2.10) параллельны.

Ответ. Прямые (2,9) и (2,10) параллельны.

Пример 3. Определить, параллельны ли прямые

и

Решение. Прямая (2.9) имеет направляющий вектор q₁=(m₁, p₁, l₁)=(1, 2, 0), а прямая (2.10) − q₂=(m₂, p₂, l₂)=(2, 4, 0). Подставляя значения m₁, p₁, l₁, m₂, p₂, l₂ в (2.8), получим

Выражение (2.13) нужно понимать так:

Как мы видим из (2.14) условия (2.13) выполняются. Следовательно прямые (2.11) и (2.12) параллельны.

Ответ. Прямые (2.11) и (2.12) параллельны.

2.3. Условие перпендикулярности прямых

Пусть φ=90°. Тогда cosφ=0. При этом выражение (2.4) примет следующий вид:

Правая часть выражения (2.15) равно нулю тогда и только тогда, когда числитель равен нулю. Следовательно, для того, чтобы прямые L₁ и L₂ были перпендикулярны , должно выполняться условие

Пример 3. Определить, перпендикулярны ли прямые

и

Решение. Прямая (2.16) имеет направляющий вектор q₁=(m₁, p₁, l₁)=(3, 2, 1), а прямая (2.17) − q₂=(m₂, p₂, l₂)=(4, −6, 0). Тогда

Удовлетворяется условие (2.16), следовательно прямые (2.17) и (2.18) перпендикулярны.

Ответ. Прямые (2.17) и (2.18) перпендикулярны.

Высота в прямоугольном треугольнике. Свойства. Как найти?

Вспомним, что высота треугольника — это перпендикуляр, опущенный из его вершины на противоположную сторону.

В прямоугольном треугольнике катеты являются высотами друг к другу. Главный интерес представляет высота, проведённая к гипотенузе.

Один из типов экзаменационных задач банке заданий ФИПИ — такие, где в прямоугольном треугольнике высота проведена из вершины прямого угла. Посмотрим, что получается:

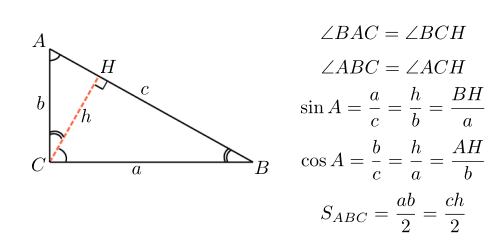
Высота проведена к гипотенузе . Она делит треугольник на два прямоугольных треугольника — и . Смотрим внимательно на рисунок и находим на нем равные углы. Это и есть ключ к задачам по геометрии, в которых высота опущена на гипотенузу.

Мы помним, что сумма двух острых углов прямоугольного треугольника равна . Значит, , то есть угол равен углу . Аналогично, угол равен углу .

Иными словами, каждый из трех углов треугольника равен одному из углов треугольника (и треугольника ). Треугольники и  называются подобными. Давайте нарисуем их рядом друг с другом.

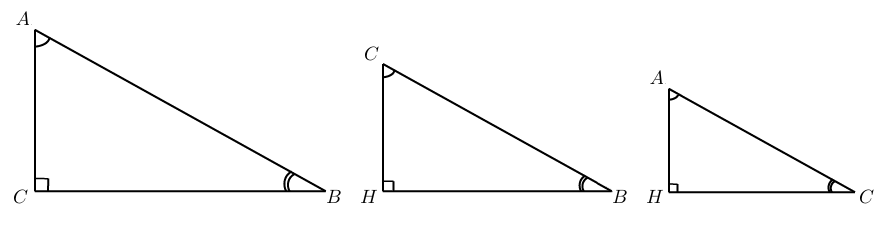
Они отличаются только размерами. Стороны подобных треугольников пропорциональны. Что это значит?

Возьмем треугольники и . Стороны треугольника длиннее, чем стороны треугольника в  раз:

При решении задач нам пригодится равенство углов треугольников и , а также пропорциональность их сторон. Обратите также внимание, что площадь треугольника можно записать двумя разными способами: как половину произведения катетов и как половину произведения гипотенузы на проведенную к ней высоту.

Ты нашел то, что искал? Поделись с друзьями!

1. В треугольнике угол  равен ,  — высота, , . Найдите .

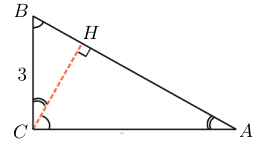
Рассмотрим треугольник . В нем известны косинус угла  и противолежащий катет . Зная синус угла , мы могли бы найти гипотенузу . Так давайте найдем :

(поскольку значение синуса острого угла положительно). Тогда:

Рассмотрим прямоугольный треугольник , . Поскольку

Отсюда

Ответ: .

2. В треугольнике угол  равен , , . Найдите высоту .

Сделайте чертеж и рассмотрите прямоугольный треугольник .

Ответ: .

3. В треугольнике угол  равен , , . К гипотенузе проведена высота . Найдите .

Это чуть более сложная задача. Ведь вам неизвестны катеты и .

Зато можно записать теорему Пифагора: .

Нам известно также, что:

Решая эту систему из двух уравнений, найдем:

Запишем площадь треугольника АВС двумя способами:

и найдем .

Найти высоту, проведенную из вершины прямого угла, можно было и другим способом. Мы выбрали самый короткий путь — составили и решили систему уравнений.