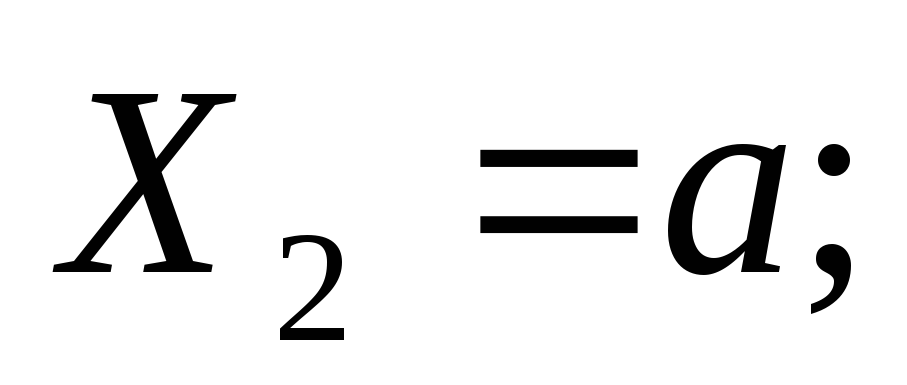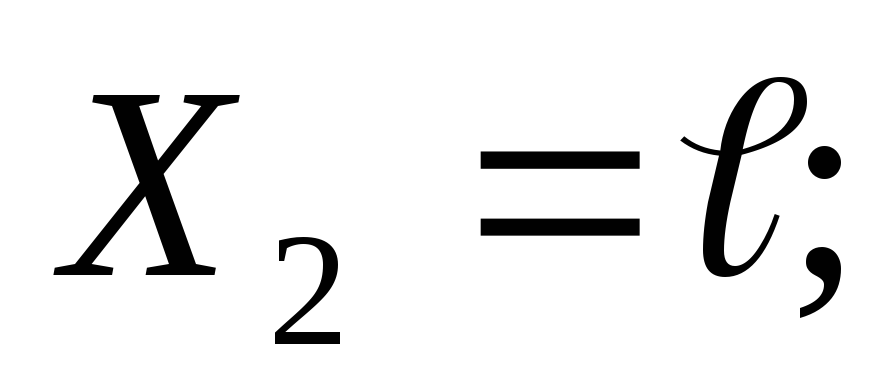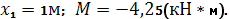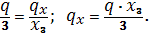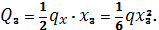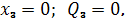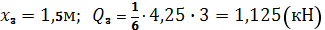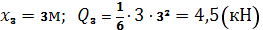Изгибающий момент — Википедия
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 23 августа 2016; проверки требуют 5 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 23 августа 2016; проверки требуют 5 правок.Изгибающий момент — момент внешних сил относительно нейтральной оси сечения балки или другого твёрдого тела.
Изгибающий момент вычисляется, как произведение приложенной статической силы (включая реакции опор) на кратчайшее расстояние от вектора этой силы до нейтральной оси сечения. Если таких сил несколько, то изгибающие моменты от каждой силы складываются с учётом знака. Отсюда понятно, что в каждом сечении тела изгибающие моменты могут различаться.
Для сечения, находящегося в равновесии, изгибающий момент равен моменту внутренних сил относительно нейтральной оси сечения. Внутренние силы можно представить, если мысленно удалить часть тела по одну сторону от сечения и заменить её внешними силами так, чтобы оставшаяся часть находилась в равновесии.
Если других воздействий нет (прямой чистый изгиб), то сечение при деформации изгиба остается плоским и поворачивается на малый угол. В реальности изгибающий момент часто сочетается со сдвигающими, растягивающими, крутящими и другими внешними силами.
Определение изгибающего момента является очень важным для расчета конструкций на прочность. При изгибающем воздействии часть стержня (волокна), расположенная по одну сторону от нейтральной оси, растягивается, а другая — сжимается. Наибольшие напряжения возникают в крайних волокнах стержня. Если они превышают прочность материала, конструкция разрушается. Связь между внутренними напряжениями и изгибающим моментом была впервые математически выражена Ш. Кулоном в 1773 году
Простейшие случаи вычисления изгибающего момента[править | править код]
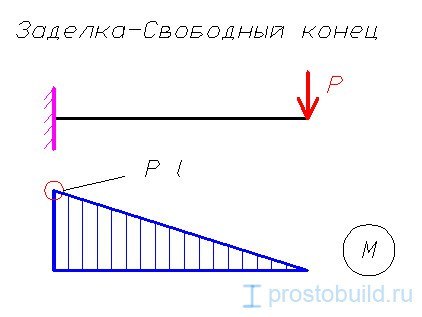
Для консоли длиной l с нагрузкой P на конце консоли изгибающий момент увеличивается от нуля на конце консоли до P*l.
Для консоли, равномерно загруженной нагрузкой q, изгибающий момент увеличивается от нуля на конце консоли до q l2 / 2.

Для балки, изображенной на рисунке,
- My(x=l/2)=F/2⋅l/2=Fl/4{\displaystyle M_{y}(x=l/2)=F/2\cdot l/2=Fl/4} .
- Волновой изгибающий момент; определяется на миделе судна, находящегося на волне
- Положительный изгибающий момент; в машиностроении принято считать положительным момент на сжатых волокнах балки, в строительстве — на растянутых
- Отрицательный изгибающий момент
- ↑ Атапин В.Г. Сопротивление материалов / Учебник и практикум для академического бакалавриата. М.:Юрайт, 2016. — 342 с. ISBN:978-5-9916-5203-2
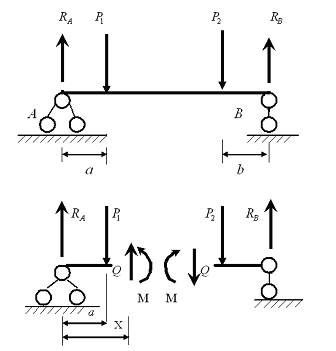
Поперечная сила и изгибающий момент.
В поперечных сечениях балки возникает поперечная сила
| Разрежем балку на расстоянии Х. Заменим действие отброшенной части (правой) внутренними усилиями Q и M; рассмотрим левую часть балки. Q – поперечная сила — результирующая всех внутренних усилий алгебраически равна сумме всех сил, расположенных левее сечения.
Составим уравнения равновесия для левой части: |
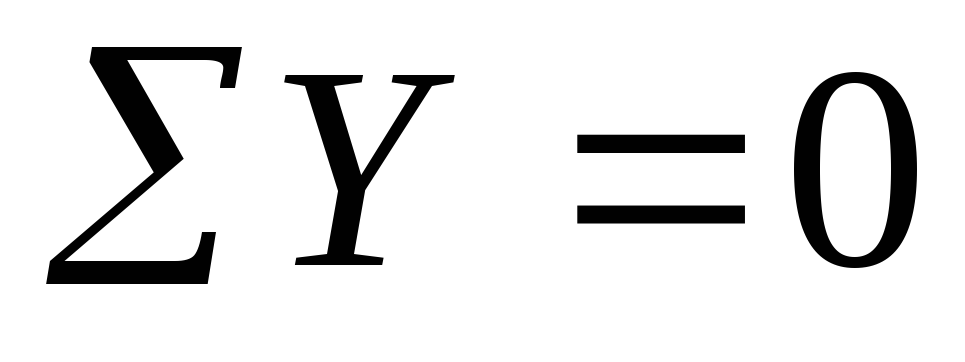 →
→ →
→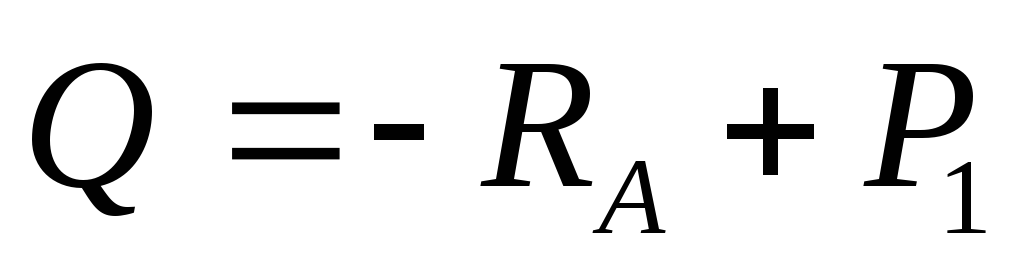
∑МсечХ=0;
→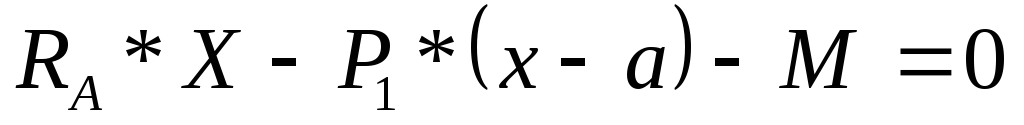 →
→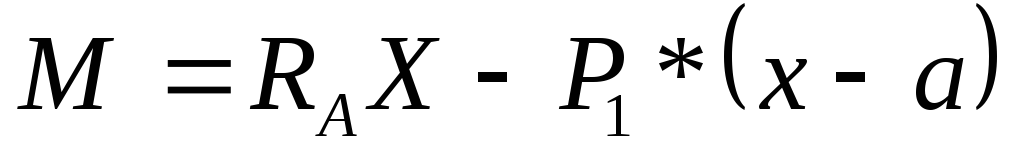
Можно вместо левой части рассмотреть правую часть. Результат будет тот же, но с обратным знаком.
В связи с этим для того, чтобы в одном и том же сечении Q и M имели одинаковые знаки независимо от того какая часть рассматривается, примем следующее
ПРАВИЛО ЗНАКОВ (см. рисунок):

Поперечную силу будем считать положительной, если равнодействующая сила левее сечения направлена вверх, а правее сечения направлена вниз.
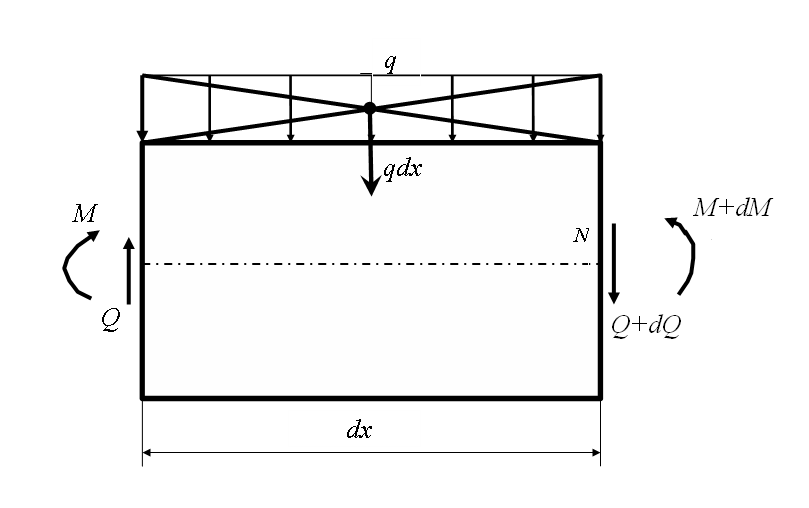
Зависимость между изгибающим моментом, поперечной силой и интенсивностью распределенной нагрузки.
| Выделим из балки участок бесконечно малой длины так чтобы по границам этого участка и по самом участке сосредоточенные силы отсутствовали. Ввиду малости участка распределенную
нагрузку Составим уравнения равновесия:
|
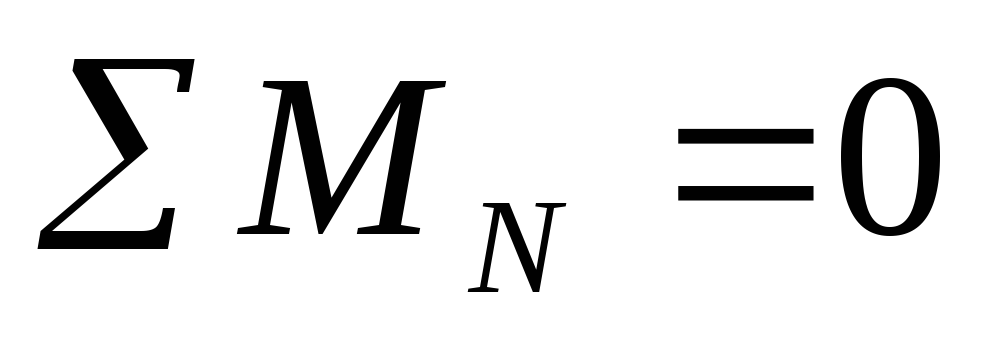 ;
; ;
;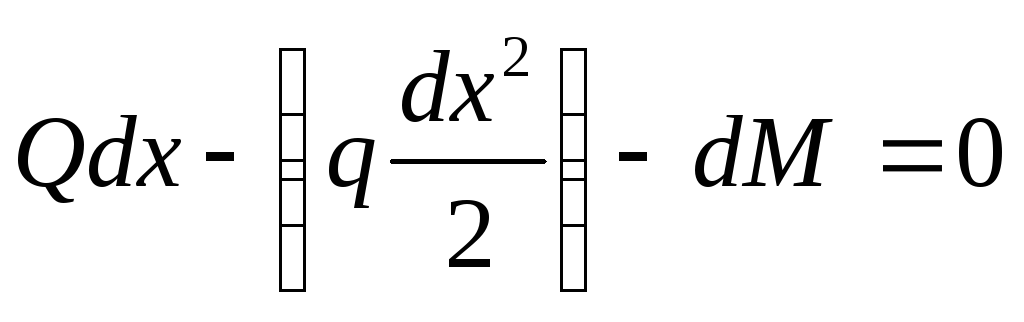
Пренебрегая бесконечно
малыми величинами второго порядка,
получаем: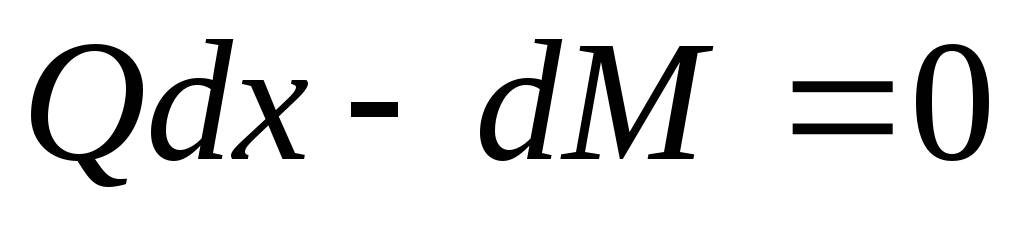 или
или
Продифференцировав последнее
выражение по Х, получаем: 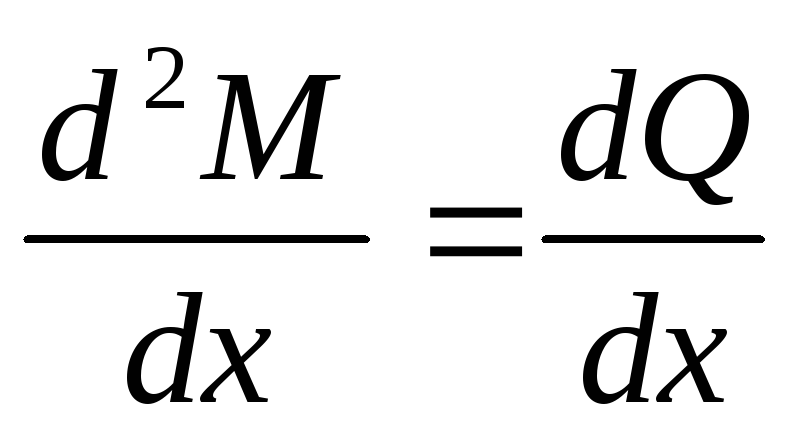 ;или
;или
Построение эпюр изгибающих моментов и поперечных сил.
Внутренние усилия Q и M зависят от координатыХ,поэтому удобно иметь графики зависимостиQ и M от расстоянияХ,эти графики называютсяэпюрамипоперечных сил и изгибающих моментов. Построение эпюрQ и M рассмотрим на частных примерах.
Положительные изгибающие моменты | Пример 1. Построить эпюры Q иM. 1) Определяем опорные реакции: 2) Разбиваем балку на участки. Рассмотрим отдельные участки. 3) Участок 1: (рассекаем на расстоянии Х1)  Участок 2: (рассекаем на расстоянии Х2) при . |
Пример 2. Построить эпюры Q иM.
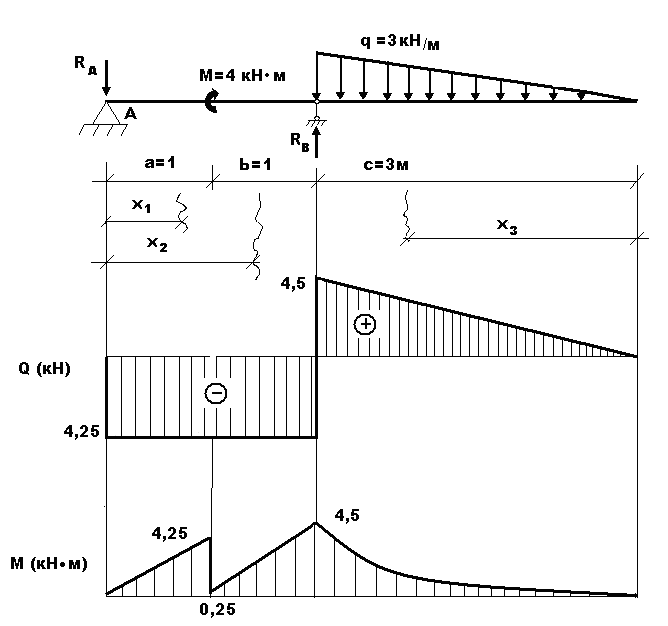
Определим опорные реакции:

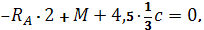
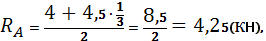
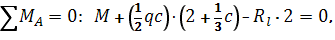
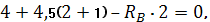
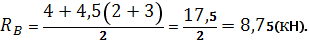
Проверка
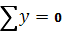
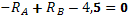 ,
,
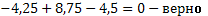
Следовательно, опорные реакции определены верно.
2) Построим эпюры QиM:
Участок I: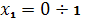
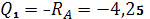
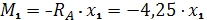
Участок II:

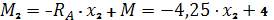
Участок III:
| Идем справа налево Из подобия треугольников . находим: |
Расчет балки на изгиб | Архитектурный журнал ADCity
Рассчитывать балку на изгиб можно несколькими вариантами:
1. Расчет максимальной нагрузки, которую она выдержит
2. Подбор сечения этой балки
3. Расчет по максимальным допустимым напряжениям (для проверки)
Давайте рассмотрим общий принцип подбора сечения балки на двух опорах загруженной равномерно распределенной нагрузкой или сосредоточенной силой.
Для начала, вам необходимо будет найти точку (сечение), в которой будет максимальный момент. Это зависит от опирания балки или же ее заделки. Снизу приведены эпюры изгибающих моментов для схем, которые встречаются чаще всего.
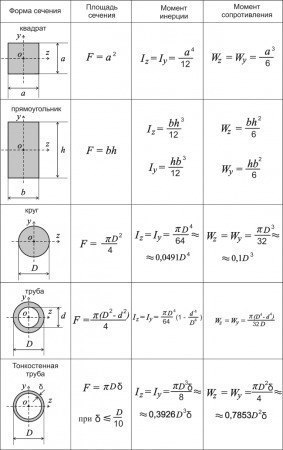
После нахождения изгибающего момента мы должны найти момент сопротивления Wx этого сечения по формуле приведенной в таблице:
Далее, при делении максимального изгибающего момента на момент сопротивления в данном сечении, мы получаем максимальное напряжение в балке и это напряжение мы должны сравнить с напряжением, которое вообще сможет выдержать наша балка из заданного материала.
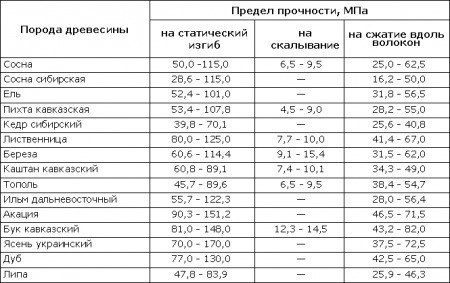
Для пластичных материалов (сталь, алюминий и т.п.) максимальное напряжение будет равно пределу текучести материала, а для хрупких (чугун) – пределу прочности. Предел текучести и предел прочности мы можем найти по таблицам ниже.
Давайте рассмотрим пару примеров:
1. Вы хотите проверить, выдержит ли вас двутавр №10 (сталь Ст3сп5) длиной 2 метра жестко заделанного в стену, если вы на нем повисните. Ваша масса пусть будет 90 кг.
Для начала нам необходимо выбрать расчетную схему.
На данной схеме видно, что максимальный момент будет в заделке, а поскольку наш двутавр имеет одинаковое сечение по всей длине, то и максимальное напряжение будет в заделке. Давайте найдем его:
P = m * g = 90 * 10 = 900 Н = 0.9 кН
М = P * l = 0.9 кН * 2 м = 1.8 кН*м
По таблице сортамента двутавров находим момент сопротивления двутавра №10.
Он будет равен 39.7 см3. Переведем в кубические метры и получим 0.0000397 м3.
Далее по формуле находим максимальные напряжения, которые у нас возникают в балке.
б = М / W = 1.8 кН/м / 0.0000397 м3 = 45340 кН/м2 = 45.34 МПа
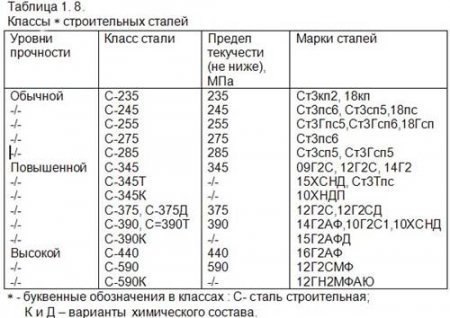
После того, как мы нашли максимальное напряжение, которое возникает в балке, то мы его может сравнить с максимально допустимым напряжением равным пределу текучести стали Ст3сп5 – 245 МПа.
45.34 МПа < 245 МПа – верно, значит данный двутавр выдержит массу 90 кг.
2. Поскольку у нас получился доволи-таки большой запас, то решим вторую задачу, в которой найдем максимально возможную массу, которую выдержит все тот же двутавр №10 длиной 2 метра.
Если мы хотим найти максимальную массу, то значения предела текучести и напряжения, которое будет возникать в балке, мы должны приравнять (б=245 Мпа = 245 000 кН*м2).
Далее по формуле б = М / W, находим максимальный момент.
М = б * W = 245 000 * 0.0000397 = 9.73 кН * м
Тогда по формуле M = P * L найдем P:
P = 9,73 кН/м / 2м = 4,87 кН = 487 кг
Итак, максимальная масса, которую выдержит двутавр №10 – 487 кг. Число это грубое, поскольку для простоты расчета мы не учитывали различные коэффициенты запаса, поэтому, чтобы подстраховаться, возьмите некий двукратный запас по прочности.








Изгибающий момент – внутренний силовой фактор

Здравствуйте. Здорово, что Вы проявляете интерес к нашему проекту SoproMats, спасибо! Эта статья будет посвящена внутреннему силовому фактору – изгибающему моменту. Фактору, который возникает в поперечных сечениях балок, работающих на изгиб. Здесь поделимся информацией как он обозначается, измеряется, определяется и т.д. В общем все, что нужно знать об изгибающем моменте. Также в конце статьи поделимся ссылочками, на важные материалы про изгибающий момент.
Что такое изгибающий момент?
Изгибающий момент – это внутренний силовой фактор, возникающий в элементах конструкций, деталях, работающих на изгиб: такие конструктивные элементы как балка, рама, плита и т.д.
Зачем нужен?
Зная изгибающий момент в сечении, а также геометрические размеры этого сечения, можно определить нормальное напряжение в его конкретной точке и исследовать ее напряженно-деформированное состояние. Определение изгибающих моментов является неотъемлемой частью любого прочностного расчета деталей, работающих на изгиб. Для наглядной визуализации распределения изгибающих моментов строят эпюры, которые позволяют выявить наиболее подверженные к разрушению места балки. Как правило, то сечение, в котором изгибающий момент имеет максимальное значение, является самым опасным у балки. За редкими исключениями. Поэтому так важно уметь определять эту величину.
Как обозначается?
Изгибающий момент обозначается буквой M с индексом, который указывает на название оси, относительного которой происходит изгиб. Обычно это ось x, поэтому в этой статье будем использовать такое обозначение — Mx.
Как определяется?
Для определения этой величины используется метод сечений. По которому считается, что если балка находится в равновесии, то и отдельные части балки также будут находится в равновесии, если действие каждой части друг на друга, заменить равными силовыми факторами. Используя этот метод в совокупности с уравнениями равновесия статики, можно определить изгибающий момент в любом сечении, более подробно посмотрим этот процесс на примере ниже.
В чем измеряется?
Данная величина измеряется в Н·м. В расчетах, в основном, используется размерность — кН·м, и этот вариант будем использовать в этой статье. Иногда считают в кгс·м и т·м.
Статьи про изгибающие моменты:
Как построить эпюру изгибающего момента? В материале этой статьи написано, как можно построить эпюру различными методами.

Задачи на изгиб | ПроСопромат.ру
Проектный и проверочный расчеты. Для балки с построенными эпюрами внутренних усилий подобрать сечение в виде двух швеллеров из условия прочности по нормальным напряжениям. Проверить прочность балки, используя условие прочности по касательным напряжениям и энергетический критерий прочности. Дано:
Покажем балку с построенными эпюрами Q и М
Согласно эпюре изгибающих моментов опасным является сечение С, в котором МС=Мmax=48,3кНм.
Условие прочности по нормальным напряжениям для данной балки имеет вид σmax=MC/WX≤σadm. Требуется подобрать сечение из двух швеллеров.
 Определим необходимое расчетное значение осевого момента сопротивления сечения:
Определим необходимое расчетное значение осевого момента сопротивления сечения:
Для сечения в виде двух швеллеров согласно сортаменту прокатной стали принимаем два швеллера №20а, момент инерции каждого швеллера Ix=1670см4, тогда осевой момент сопротивления всего сечения:
Перенапряжение (недонапряжение) в опасных точках посчитаем по формуле: Тогда получим недонапряжение:
Тогда получим недонапряжение:

Теперь проверим прочность балки, исходя из условия прочности по касательным напряжениям. Согласно эпюре поперечных сил опасными являются сечения на участке ВС и сечение D. Как видно из эпюры, Qmax=48,9 кН.
Условие прочности по касательным напряжениям имеет вид:
Для швеллера №20 а: статический момент площади Sx1=95,9 см3, момент инерции сечения Ix1=1670 см4, толщина стенки d1=5,2 мм, средняя толщина полки t1=9,7 мм, высота швеллера h1=20 см, ширина полки b1=8 см.
Для поперечного сечения из двух швеллеров:
Sx= 2Sx1=2·95,9=191,8 см3,
Ix=2Ix1=2·1670=3340 см4,
b=2d1=2·0,52=1,04 см.
Определяем значение максимального касательного напряжения:
τmax=48,9·103·191,8·10−6/3340·10−8·1,04·10−2=27МПа.
Как видно, τmax <τadm (27МПа<75МПа).
Следовательно, условие прочности выполняется.
Проверяем прочность балки по энергетическому критерию.
Из рассмотрения эпюр Q и М следует, что опасным является сечение С, в котором действуют MC=Mmax=48,3 кНм и QC=Qmax=48,9 кН.
Проведем анализ напряженного состояния в точках сечения С

Схема сечения балки и эпюры напряжений для анализа напряженного состояния
Определим нормальные и касательные напряжения на нескольких уровнях (отмечены на схеме сечения)
Уровень 1-1: y1-1=h1/2=20/2=10см.
Нормальные и касательные напряжения:
Главные напряжения:

Экстремальные касательные напряжения:
Уровень 2−2: y2-2=h1/2−t1=20/2−0,97=9,03см.
Нормальные и касательные напряжения:
Главные напряжения:
Экстремальные касательные напряжения:
Уровень 3−3: y3-3=h1/2−t1=20/2−0,97=9,03см.
Нормальные и касательные напряжения:
Главные напряжения:
Экстремальные касательные напряжения:
Уровень 4−4: y4-4=0.
Нормальные и касательные напряжения: (в середине нормальные напряжения равны нулю, касательные максимальны, их находили в проверке прочности по касательным напряжениям)
(в середине нормальные напряжения равны нулю, касательные максимальны, их находили в проверке прочности по касательным напряжениям)
Главные напряжения:
Экстремальные касательные напряжения:
Уровень 5−5:
Нормальные и касательные напряжения:
Главные напряжения:
Экстремальные касательные напряжения:
Уровень 6−6:
Нормальные и касательные напряжения:
Главные напряжения:
Экстремальные касательные напряжения:
Уровень 7−7:
Нормальные и касательные напряжения:
Главные напряжения:
Экстремальные касательные напряжения:
В соответствии с выполненными расчетами эпюры напряжений σ, τ, σ1, σ3, τmax и τmin представлены на рис. Схема сечения балки и эпюры напряжений для анализа напряженного состояния
Анализ этих эпюр показывает, что в сечении балки опасными являются точки на уровне 3-3 (или 5-5), в которых: 
Используя энергетический критерий прочности, получим

Из сравнения эквивалентного и допускаемого напряжений следует, что условие прочности также выполняется 
(135,3 МПа<150 МПа).
Построение эпюры изгибающих моментов — Лекции и примеры решения задач технической механики
Рассмотрим порядок построения эпюры изгибающих моментов Mx для консольной балки с жесткой заделкой.
Ранее для данной балки уже были рассмотрены примеры определения опорных реакций и построения эпюры поперечных сил Qy.
Покажем найденные опорные реакции и выбранную систему координат.
Для построения эпюры изгибающих моментов Mx запишем их выражение по каждому силовому участку и рассчитаем их значения на границах участков. При этом воспользуемся методом сечений.
Наш видеоурок построения эпюр внутренних силовых факторов для балки:
Расчеты для построения эпюр балки
Нумерацию силовых участков балки, сечения и другие вспомогательные обозначения примем из расчета эпюры Qy.
Рассмотрим I силовой участок:
Выбрав левую часть балки, отбросим ненадолго правую, и запишем имеющиеся данные.
I с.у. (AB) 0 ≤ z1≤ 0,5м
Внутренний изгибающий момент в указанном сечении равен сумме всех внешних моментов, воздействующих на рассматриваемую часть балки.
Здесь на момент в рассматриваемом сечении влияют только опорные реакции M и R, то есть сумма моментов состоит из двух слагаемых.
По правилу знаков момент, который стремится сжать верхние слои балки, принимается положительным, следовательно:
MxI=Σmi=M+R∙z1=30+60z1
В выражении переменная z1 в первой степени, поэтому эпюра Mx на первом участке будет иметь вид прямой линии.
Видео про знаки моментов при изгибе
Рассчитаем значения MxI на границах участка, т.е. при z1=0 и при z1=0,5м
MxI (z1=0)=30кНм
MxI (z1=0,5м)=60кНм
Переходим на второй силовой участок:
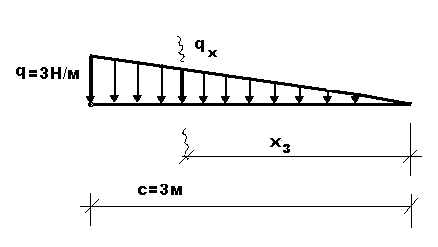
Рассекаем балку в произвольном месте участка и рассматриваем её правую часть.
Эта часть балки изгибается силой F и распределенной нагрузкой q.
II с.у. (BC) 0 ≤ z2 ≤ 1м
MxII=Σmi=-q∙z2(z2/2)+F∙z2= -50∙z22+40∙z2
Получено выражение с переменной z2 во второй степени, значит, эпюра Mx на втором участке будет иметь вид параболы.
Видео про построение эпюр
Для построения параболы требуется как минимум три точки. Этими точками будут значения Mx на границах и в середине II силового участка, то есть при z2=0, z2=1м и z2=0,5м.
MxII(z2=0)=0
MxII(z2=0,5м)=7,5кНм
MxII(z2=1м)= -10кНм
По полученным данным строим эпюру изгибающих моментов Mx (готовую эпюру Qy перенесем из ранее рассмотренной задачи)
I с.у. (AB) 0 ≤ z1 ≤ 0,5м.
MxI=30+60z1 (прямая)
MxI(z1=0)=30кНм
MxI(z1=0,5м)=60кНм
II с.у. (BC) 0 ≤ z2 ≤ 1м
MxII= -50z22+40z2 (парабола)
MxII(z2=0)=0
MxII(z2=0,5м)=7,5кНм
MxII(z2=1м)= -10кНм
Прежде чем соединять отмеченные точки эпюры параболой, обратите внимание на эпюру поперечных сил Qy.
Qy — первая производная от Mx. Поэтому в том месте, где Qy пересекает базовую линию (т.е. Qy=0) на эпюре Mx будет экстремум.
Видео про расчет экстремума эпюры
Рассчитаем значение экстремума эпюры Mx на II участке балки.
Для этого:
- Выражение QyII приравняем к нулю
QyII=100z2-40=0 - Выразим из него z2
z2=40/100=0,4м - Подставим z2 в выражение для MxII
MxIIэкстр(z2=0,4м)= -50∙0,42+40∙0,4=8кНм
Отметив эту точку в области эпюры где Qy=0 соединим ее с тремя другими параболой.
Эпюра изгибающих моментов построена. Проверка эпюры Mx.
Расчеты на прочность >
Другие примеры решения задач >


 примем равномерно распределенной
примем равномерно распределенной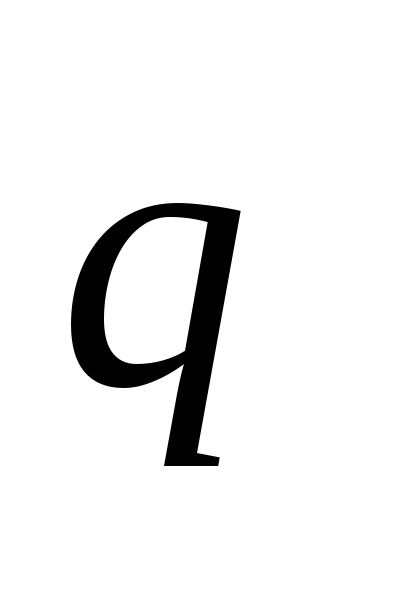 .
.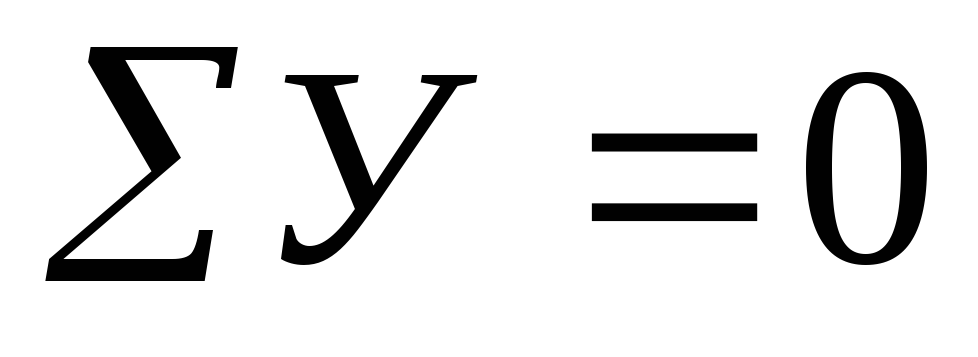 ;
;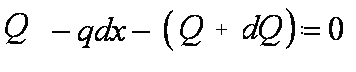
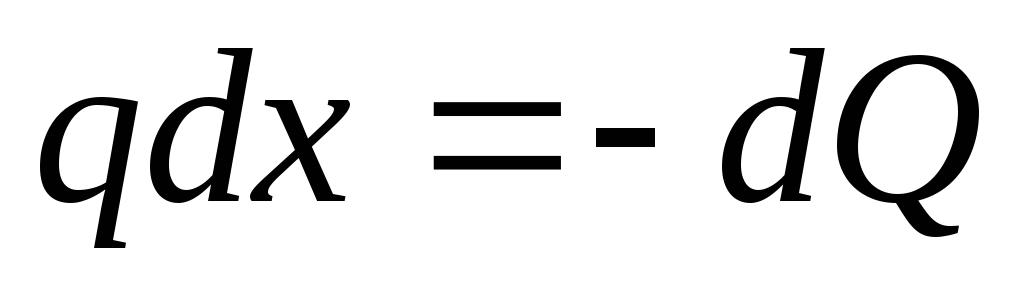
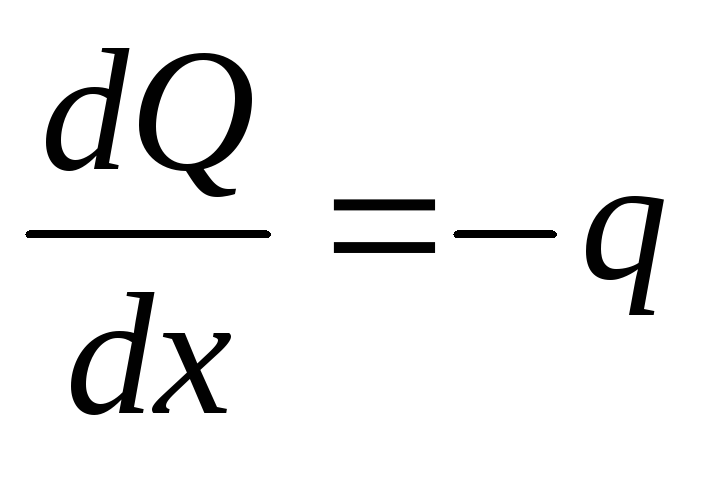
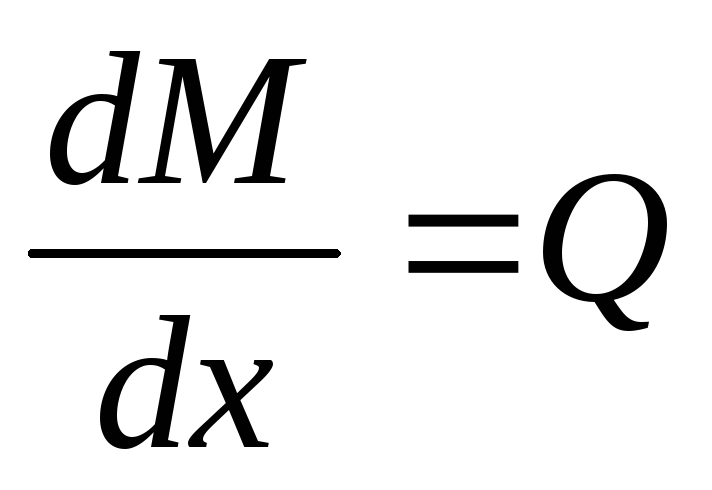
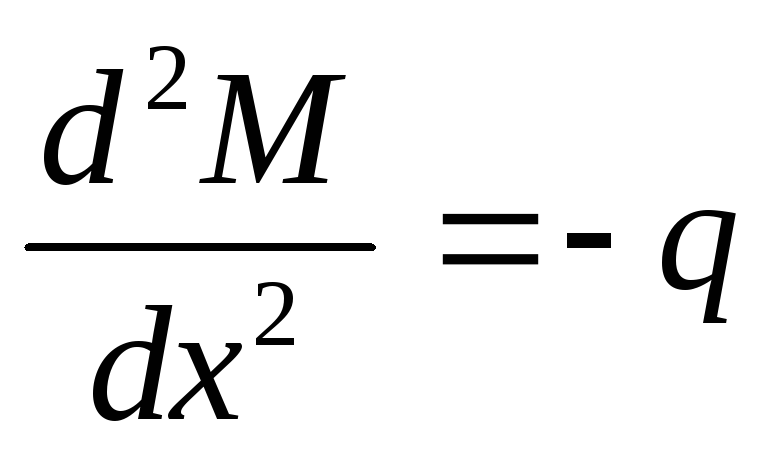


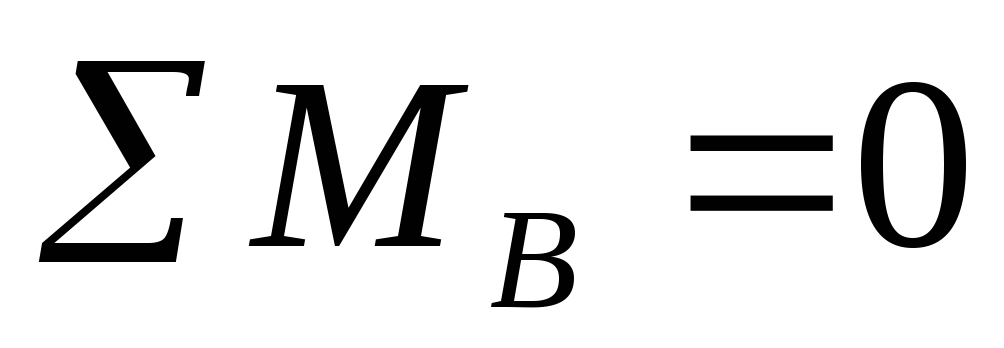 ;
;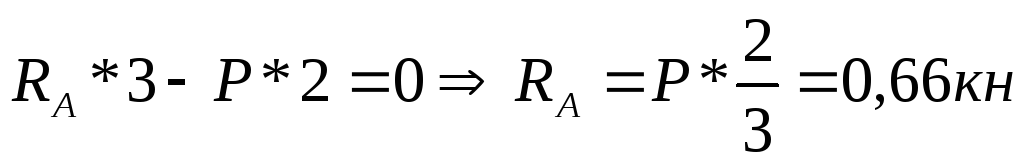
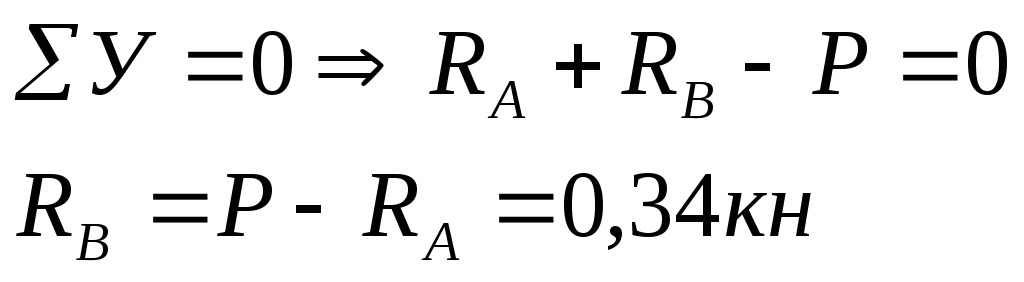
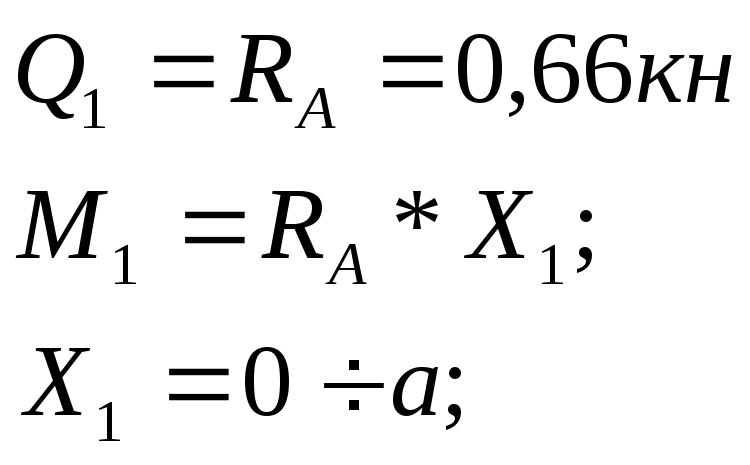
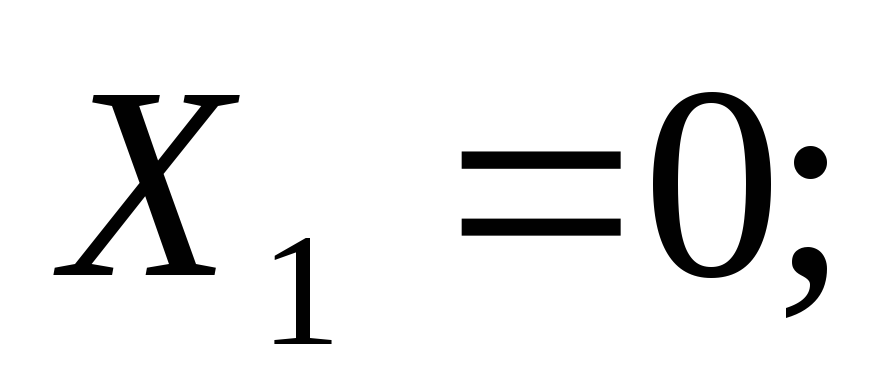


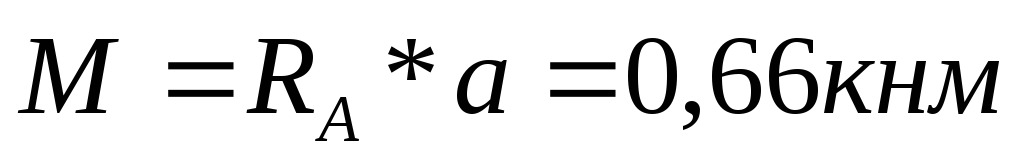
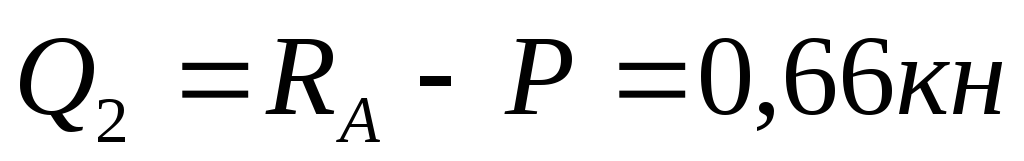
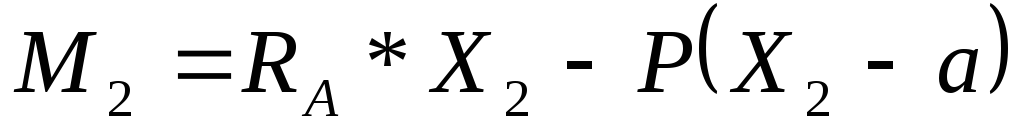
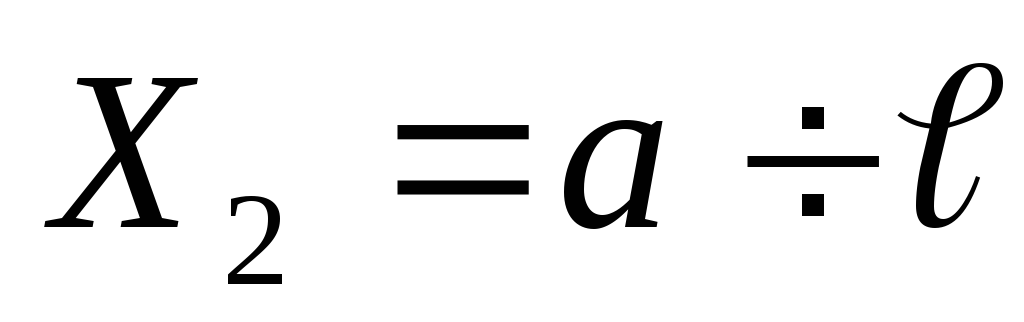
 при
при