Какой угол 90 градусов – Углы 0°,30°,45°,60°,90°,180°,270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π). Синусы, косинусы, тангенсы и котангенсы. Таблица значений тригонометрических функций.

Как проверить прямой угол без угольника

При отделочных работах и строительстве бывает нужна четкая геометрия: перпендикулярные стены и иные конструкции, требующие прямого угла в 90 градусов. Обыкновенный угольник не может позволить проверить или разметить углы со сторонами в несколько метров. Описываемый же метод превосходно подходит для разметки или проверки любых углов — длинна сторон не ограничена. Основной инструмент для измерений — рулетка.

Мы будем рассматривать точную разметку прямого угла, а также метод проверки уже размеченных углов на стенах и других объектах.

Теорема Пифагора

Теорема основана на утверждении, что у прямоугольного треугольника сумма квадратов длин катетов равна квадрату длины гипотенузы. В виде формулы записывается это так:

a²+b²=c²

Стороны a и b — катеты, между которыми угол равен ровно 90 градусов. Следовательно, сторона c — гипотенуза. Подставляя в эту формулу две известные величины, мы можем вычислить третью, неизвестную. А следовательно можем размечать прямые углы, а также проверять их.

Теорема Пифагора известна еще под названием «египетский треугольник». Это треугольник со сторонами 3, 4 и 5, причем совершенно не важно, в каких единицах длинны. Между сторонами 3 и 4 — ровно девяносто градусов. Проверим данное утверждение вышеприведенной формулой: a²+b²=c² = (3×3)+(4×4) = 9+16 = (5×5) = 25 — все сходится!

А теперь применим теорему на практике.

Проверка прямого угла

Начнем с самого простого — проверки прямого угла с помощью теоремы Пифагора. Самым частым примером в отделке и строительстве является проверка перпендикулярности стен. Перпендикулярные стены — это стены, расположенные друг к другу под прямым углом 90°.

Итак, берем любой проверяемый внутренний угол. На стенах (на одной высоте) или на полу отмечаем на обоих стенах отрезки произвольных длин. Длинна этих отрезков произвольная, по возможности нужно отмечать как можно больше, но чтобы между отметками на стенах удобно было мерить диагональ. Например, мы отметили 2,5 метра (или 250 см.) на одной стене и 3 метра (или 300 см.) на другой. Теперь длину отрезка каждой стены возводим в квадрат (умножаем саму на себя) и получившиеся произведения складываем. Выглядит это так: (2,5×2,5)+(3×3)=15,25 — это диагональ в квадрате. Теперь нужно извлечь из этого числа квадратный корень √15,25≈3,90 — 3,9 метра должна составлять диагональ между нашими отметками. Если измерение рулеткой показывает другую длину диагонали — проверяемый угол развернут и имеет отклонение от 90°.

Калькулятор расчета диагонали прямого угла

Извлечение квадратного корня никогда меня не привлекало — простому человеку не обойтись без калькулятора, к тому же, не на всех мобильных устройствах калькуляторы умеют извлекать его. Поэтому можно пользоваться упрощенным методом. Нужно лишь запомнить: у прямого угла со сторонами ровно 100 сантиметров, диагональ равна 141,4 см.

Таким образом, у прямого угла со сторонами 2 м. — диагональ равна 282,8 см. То есть на каждый метр плоскости приходится 141,4 см. У этого метода один недостаток: от измеряемого угла нужно откладывать одинаковые расстояния на обеих стенах и отрезки эти должны быть кратны метру. Не буду утверждать, но по моей скромной практике — это гораздо удобнее. Хотя не стоит забывать о первоначальном способе совсем — в некоторых случаях он очень актуален.

Сразу же возникает вопрос: какое отклонение от вычисленной длинны диагонали считать нормой (погрешностью), а какое нет? Если проверяемый угол с отмеченными сторонами по 1 м. будет 89°, то диагональ уменьшится до 140 см. Из понимания этой зависимости можно сделать объективный вывод, что погрешность диагонали 141,4 см. в несколько миллиметров не даст отклонения в один целый градус.

Как проверить внешний угол? Проверка внешнего угла по сути не отличается, нужно лишь продлить линии каждой стены на полу (или земле, при помощи шнура) и получившийся внутренний угол измерить обычным способом.

Как разметить прямой угол рулеткой

Разметка может основываться как на общей теореме Пифагора, так и на принципе «египетского треугольника». Однако это только в теории линии просто чертятся на бумаге, «ловить» же все выбранные размеры растянутыми шнурами или линиями на полу — задача посложнее.

Поэтому я предлагаю упрощенный способ, основанный на диагонали 141,4 см. у треугольника со сторонами 100 см. Вся последовательность разметки изображена на картинках ниже. Важно не забывать: диагональ 141,4 см. нужно умножать на количество метров в отрезке А-Б. Отрезки А-Б и А-В должны быть равны и соответствовать целому числу в метрах. Картинки увеличиваются по клику!

Как разметить острый угол

Гораздо реже возникает надобность в создании острых углов, в частности 45°. Для формирования подобных фигур формулы более сложные, однако это не самое проблематичное. Гораздо сложнее свести все линии, начерченные или натянутые шнурами — дело это непростое. Поэтому я предлагаю использовать упрощенный метод. Сначала размечается прямой угол 90°, а затем диагональ 141,4 делится на нужное количество равных частей. Например, чтобы получить 45°, диагональ нужно поделить пополам и от точки А провести линию через место деления. Таким образом мы получим два угла по 45 градусов. Если поделить диагональ на 3 части, то получится три угла по 30 градусов. Думаю алгоритм вам понятен.

Собственно я рассказал все, что мог рассказать, надеюсь все изложил понятным языком и у вас больше не возникнет вопросов как размечать и проверять прямые углы. Стоит добавить, что уметь делать это должен любой отделочник или строитель, ведь полагаться на строительный угольник небольшого размера — непрофессионально.

Оцените публикацию:

Оценка: 4.5 (34 голосов)

Смотрите так же другие статьи

Как найти прямой угол 90 градусов. Сделать и построить самому угол 90°

Многие строители сталкиваются с такой проблемой — как найти угол 90 градусов с помощью строительной рулетки и карандаша?

Давайте рассмотрим как на практике любой желающий в течение нескольких минут может с помощью строительной рулетки и карандаша сделать точный угольник с прямым углом, то есть 90°.

Технология получения треугольника с прямым углом

Прямой угол

1. Для начала определимся с системой исчесления, к примеру будем считать в «см».

2. Придумываем любое число, например 20.

Примечание: Здесь может быть любое число на ваше усмотрение. Чем больше число, тем больше размер самого треугольника.

3. Берем комбинацию чисел «3, 4, 5» и последовательно умножаем каждое из этих чисел на придуманное нами число 20.

4. Получаются следующие числа: 60, 80, 100.

5. Присваиваем их поочередно к сторонам треугольника:

• Первый кактет 60 см
• Второй кактет 80 см
• Гипотенуза 100 см.

6. Пользуемся.

Как сделать самому угольник с прямым углом за 5 минут?

1. Соединяем между собой две ровные деревянные рейки, так чтобы одна из них была перпендикулярна другой.

2. Измеряем два катета по выше изложенной системе.

3. Прибиваем деревянную рейку к первой метке.

4. Измеряем гипотенузу и фиксируем на втором катете.

5. Проверяем все размеры и во всех местах дополнительно фиксируем.

6. Лишние части отрезаем.

винперстostankinobest app for tradingonline financial software

Градус (геометрия) — Википедия

У этого термина существуют и другие значения, см. Градус.

Гра́дус, мину́та, секу́нда — общепринятые единицы измерения плоских углов. Также эти величины используются в картографии для определения координат произвольной точки земной поверхности, а также для определения азимута.

Окружность с хордой, образованной стороной равностороннего треугольника (выделена красным). Одна шестидесятая этой дуги равна одному градусу. Шесть таких хорд охватывают полный круг.

Градус (от лат. gradus — деление шкалы, шаг, ступень) обозначается °. Один полный оборот соответствует углу в 360°. В прямом угле, таким образом, 90°, в развёрнутом — 180°.

Причина выбора градуса как единицы измерения углов неизвестна. Одна из теорий предполагает, что это связано с тем, что 360 — приблизительное количество дней в году^[1]. Некоторые древние календари, такие как древнеперсидский, использовали год в 360 дней.

Другая теория гласит, что аккадцы (вавилоняне) поделили окружность, используя угол равностороннего треугольника как базу и поделив результат на 60, следуя своей шестидесятеричной системе счисления^[2][3].

Если построить окружность радиусом 57 см, то 1 градус будет примерно соответствовать 1 см длины дуги данной окружности.

Градус в альтернативных единицах измерения:

1∘=2π360{\displaystyle 1^{\circ }={\frac {2\pi }{\displaystyle {360}}}} радиан =π180=1p≈157,295779513∘{\displaystyle ={\frac {\pi }{\displaystyle {180}}}={\frac {1}{\displaystyle {p}}}\approx {\frac {1}{\displaystyle {57{,}295779513^{\circ }}}}}^[4]≈0,0174532925{\displaystyle \approx 0{,}0174532925} (радиан в 1°)

1∘=1360{\displaystyle 1^{\circ }={\frac {1}{360}}} оборота=0,002(7) оборота=0,002777777777…

1∘=400360{\displaystyle 1^{\circ }={\frac {400}{360}}} градов=1,(1) градов=1,11111111111… градов

По аналогии с делением часа как интервала времени градус делят на 60 минут (от лат. minutus — маленький, мелкий; обозначается штрихом x′), а минуту — на 60 секунд (от лат. secunda divisio — второе деление; обозначается двумя штрихами y″. Ранее употреблялась величина в 1/60 секунды — терция (третье деление), с обозначением тремя штрихами — z″′. Деление градуса на минуты и секунды ввёл Клавдий Птолемей^[5]; корни же такого деления восходят к учёным Древнего Вавилона (где использовалась шестидесятеричная система счисления).

Минуты и секунды в других системах измерения:

1′=2π360∘⋅60′=1′p′≈1′3437,747′{\displaystyle 1’={\frac {2\pi }{\displaystyle {360^{\circ }}\cdot 60′}}={\frac {1′}{p’}}\approx {\frac {1′}{3437{,}747′}}}^[4]≈2,90888208⋅10−4 rad{\displaystyle \approx 2{,}90888208\cdot 10^{-4}~{\text{rad}}} (1 минута в радианах)

1″=2π360∘⋅60′⋅60″=1″p″≈1″206264,8″{\displaystyle 1»={\frac {2\pi }{\displaystyle {360^{\circ }}\cdot 60’\cdot 60»}}={\frac {1»}{p»}}\approx {\frac {1»}{206264{,}8»}}}^[4]≈4,848136811⋅10−6 rad{\displaystyle \approx 4{,}848136811\cdot 10^{-6}~{\text{rad}}} (1 секунда в радианах).

Минуты и секунды в радианной мере из-за своих чрезмерно малых величин представляют ограниченный интерес и практически очень мало используются.
Гораздо больший интерес представляет перевод десятичных (сотых, десятитысячных) долей градуса в минуты и секунды и обратно — см. Радиан#Связь радиана с другими единицами и Географические координаты.

Угловая секунда[править | править код]

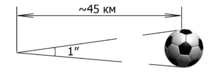
Углова́я секу́нда (англ. arcsecond, arc second, as, second of arc; синонимы: дуговая секунда, секунда дуги^[6]) — внесистемная астрономическая единица измерения малых углов, тождественная секунде плоского угла^[7].

Использование[править | править код]

Угловая секунда (обозначается ″) используется в астрономии при измерении плоских углов в градусных мерах. При измерении углов в часовых мерах (в частности, для определения прямого восхождения) используется единица измерения «секунда» (обозначается ^s). Соотношение между этими величинами определяется формулой 1^s=15″.^[8]

Иногда угловую секунду (и производные от неё дольные единицы) ошибочно называют арксекундой^[6][9], что является простой транслитерацией с англ. arcsecond.

Дольные единицы[править | править код]

По аналогии с международной системой единиц (СИ), наряду с угловой секундой применяются и её дольные единицы измерения: миллисекунды (англ. milliarcseconds, mas), микросекунды (англ. microarcseconds, µas) и пикосекунды (англ. picoarcseconds, pas). Они не входят в СИ (СИ рекомендует миллирадианы и микрорадианы), но допускаются к применению^[7]. Однако согласно ГОСТ 8.417-2002, наименование и обозначения единиц плоского угла (градус, минута, секунда) не допускается применять с приставками^[10], в связи с чем такие дольные величины должны приводиться либо к единицам СИ (миллирадианам и т. п.), либо к угловым секундам, либо обозначаться исходными единицами (mas, µas и pas соответственно).

Связь различных угловых единиц измерения

Единица	Величина	Обозначение	Аббревиатура	Радиан (прибл.)
градус	1/360 окружности	°	deg	17,4532925 mrad
минута	1/60 градуса	′	arcmin, amin, ′^{\displaystyle {\hat {‘}}}, MOA	290,8882087 µrad
секунда	1/60 минуты	″	arcsec	4,8481368 µrad
миллисекунда	1/1000 секунды		mas	4,8481368 nrad
микросекунда	1 × 10−6 секунды		μas	4,8481368 prad

Дольные единицы могут использоваться для обозначения собственного движения звёзд и галактик, годичного параллакса и углового диаметра звёзд.

Для наблюдения астрономических объектов под такими сверхмалыми углами астрономы прибегают к методу интерферометрии, при котором сигналы, принимаемые несколькими разнесёнными радиотелескопами, комбинируются в процессе апертурного синтеза. Так, используя методику интерферометрии со сверхдлинной базой, астрономы получили возможность измерить собственное движение галактики Треугольника.^{[источник не указан 2752 дня]}

В видимом свете существенно труднее достичь миллисекундного разрешения. Тем не менее, спутник Hipparcos справился с этой задачей в процессе астрометрических измерений, по результатам которых были составлены наиболее точные (по состоянию на 1997 год) каталоги звёзд Tycho (TYC) и Hipparcos (HIP)^[11][12].

1. ↑ Weisstein, Eric W. Degree (англ.). Wolfram MathWorld. Дата обращения 26 ноября 2017.
2. ↑ James Hopwood Jeans. The Growth of Physical Science. — 1947. — С. 7.
3. ↑ Murnaghan, Francis D. Analytic geometry. — New York: Prentice-Hall, inc., 1946. — P. 2.
4. ↑ ^{1 2 3} Переводные множители — <57,295779513>, <3437,747>, <206264,8> — см. Радиан#Связь радиана с другими единицами.
5. ↑ Боголюбов, 1983, с. 393—394.
6. ↑ ^{1 2} Англо-русско-английский астрономический словарь (неопр.). Astronet. Дата обращения 23 декабря 2007.
7. ↑ ^{1 2} Non-SI units accepted for use with the International System of Units (англ.). SI brochure (8th ed.). Bureau International des Poids et Mesures. — Описание СИ на сайте Международного бюро мер и весов. Дата обращения 23 декабря 2007. Архивировано 23 августа 2011 года.
8. ↑ Справочник. Некоторые внесистемные единицы (неопр.). ASTROLAB. Дата обращения 23 декабря 2007.
9. ↑ Glossary entry for English term «arcsecond» (англ.). Справочник по услугам профессионального перевода, предоставляемым независимыми переводчиками и бюро перевода. ProZ.com. Дата обращения 23 декабря 2007. Архивировано 23 августа 2011 года.
10. ↑ ГОСТ 8.417-2002. Единицы величин. Введён в действие с 1 сентября 2003 г. // Информационная система по оборудованию «Прибор.Инфо» : справочник. — 2003. Архивировано 5 августа 2013 года.
11. ↑ Гурьянов С. Почему звезды называются именно так? (неопр.). проект «Астрогалактика» (29 октября 2005 года). Дата обращения 26 декабря 2007.
12. ↑ Цветков А. С. Общие сведения о проекте Hipparcos // Руководство по практической работе с каталогом Hipparcos. — СПб.: АИ СПбГУ.

Прямой, тупой, острый и развернутый угол

Давайте начнем с определения того, что такое угол. Во-первых, он является геометрической фигурой. Во-вторых, он образован двумя лучами, которые называются сторонами угла. В-третьих, последние выходят из одной точки, которую называют вершиной угла. Исходя из этих признаков, мы можем составить определение: угол — геометрическая фигура, которая состоит из двух лучей (сторон), выходящих из одной точки (вершины).

Их классифицируют по градусной величине, по расположению относительно друг друга и относительно окружности. Начнем с видов углов по их величине.

Существует несколько их разновидностей. Рассмотрим подробнее каждый вид.

Основных типов углов всего четыре — прямой, тупой, острый и развернутый угол.

Прямой

Он выглядит так:

Его градусная мера всегда составляет 90^о, иначе говоря, прямой угол — это угол 90 градусов. Только они есть у таких четырехугольников, как квадрат и прямоугольник.

Тупой

Он имеет такой вид:

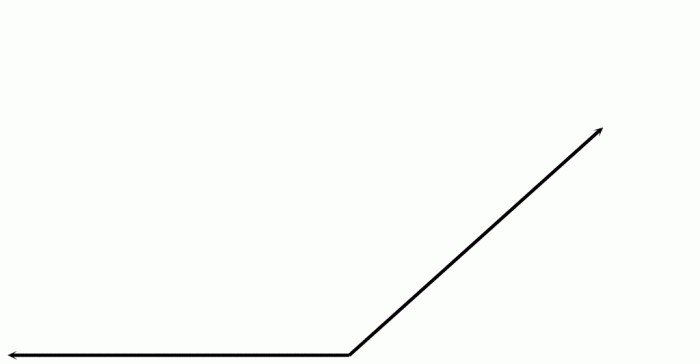
Градусная мера тупого угла всегда больше 90^о, но меньше 180^о. Он может встречаться в таких четырехугольниках, как ромб, произвольный параллелограмм, во многоугольниках.

Острый

Он выглядит так:

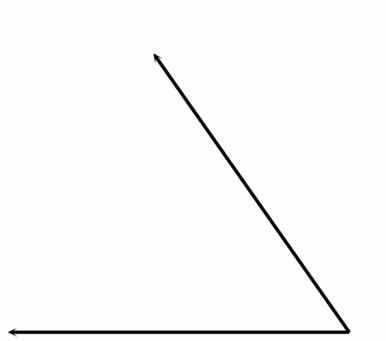
Градусная мера острого угла всегда меньше 90^о. Он встречается во всех четырехугольниках, кроме квадрата и произвольного параллелограмма.

Развернутый

Развернутый угол имеет такой вид:

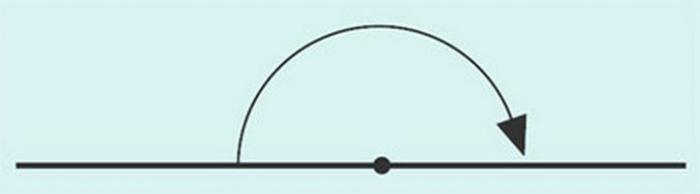
В многоугольниках он не встречается, но не менее важен, чем все остальные. Развернутый угол — это геометрическая фигура, градусная мера которой всегда равняется 180º. На нем можно построить смежные углы, проведя из его вершины один или несколько лучей в любых направлениях.

Есть еще несколько второстепенных видов углов. Их не изучают в школах, но знать хотя бы об их существовании необходимо. Второстепенных видов углов всего пять:

1. Нулевой

Он выглядит так:

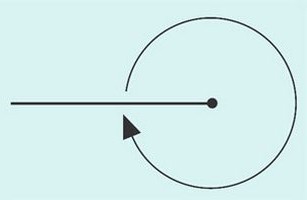
Само название угла уже говорит о его величине. Его внутренняя область равняется 0^о, а стороны лежат друг на друге так, как показано на рисунке.

2. Косой

Косым может быть и прямой, и тупой, и острый, и развернутый угол. Главное его условие — он не должен равняться 0^о, 90^о, 180^о, 270^о.

3. Выпуклый

Выпуклыми являются нулевой, прямой, тупой, острый и развернутый углы. Как вы уже поняли, градусная мера выпуклого угла — от 0^о до 180^о.

4. Невыпуклый

Невыпуклыми являются углы с градусной мерой от 181^о до 359^о включительно.

5. Полный

Полным является угол с градусной мерой 360^о.

Это все типы углов по их величине. Теперь рассмотрим их виды по расположению на плоскости относительно друг друга.

1. Дополнительные

Это два острых угла, образовывающие один прямой, т.е. их сумма 90^о.

2. Смежные

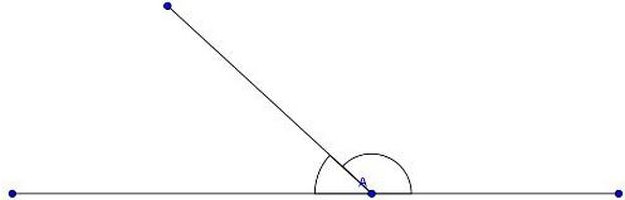
Смежные углы образуются, если через развернутый, точнее, через его вершину, провести луч в любом направлении. Их сумма равна 180^о.

3. Вертикальные

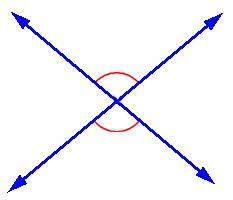
Вертикальные углы образуются при пересечении двух прямых. Их градусные меры равны.

Теперь перейдем к видам углов, расположенным относительно окружности. Их всего два: центральный и вписанный.

1. Центральный

Центральным является угол с вершиной в центре окружности. Его градусная мера равна градусной мере меньшей дуги, стянутой сторонами.

2. Вписанный

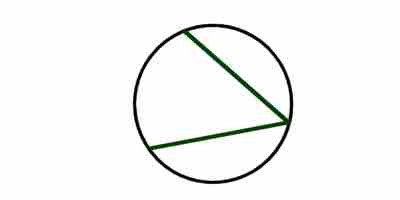
Вписанным называется угол, вершина которого лежит на окружности, и стороны которого ее пересекают. Его градусная мера равна половине дуги, на которую он опирается.

Это все, что касается углов. Теперь вы знаете, что помимо наиболее известных — острого, тупого, прямого и развернутого — в геометрии существует много других их видов.