Как вычислить градус угла – Градусная мера угла / Начальные геометрические сведения / Справочник по геометрии 7-9 класс

Нахождение углов треугольника по заданным сторонам

От нашего пользователя поступил запрос на создание калькулятора, рассчитывающего углы треугольника по заданным сторонам — Расчет углов треугольника.

Для треугольника, в отличие от, скажем, четырехугольника, эта задача имеет решение, ибо треугольник можно однозначно определить по трем сторонам (а также по двум сторонам и углу между ними, и по стороне и двум прилежащим углам).

Стороны в треугольнике, кстати сказать, должны следовать неравенству треугольника, то есть, сумма любых двух сторон должна быть больше третьей стороны.
Математически (см. рисунок) это выражается системой

В случае невыполнения хотя бы одного из условий треугольник называют вырожденным. Собственно, это и не треугольник уже.

Идем дальше — при известных сторонах углы проще всего определить, пользуясь теоремой косинусов, частным случаем которой является теорема Пифагора (см. рисунок)

, откуда

Калькулятор ниже рассчитывает углы по введенным длинам сторон. Если треугольник вырожденный, то в результате будут нули.

Нахождение углов треугольника по заданным сторонам

Точность вычисления

Знаков после запятой: 2

Угол alpha (градусы)

 

Угол beta (градусы)

 

Угол gamma (градусы)

 

save Сохранить share Поделиться extension Виджет

Как найти углы прямоугольного треугольника

Чтобы найти углы прямоугольного треугольника воспользуйтесь нашим очень удобным онлайн калькулятором:

Онлайн калькулятор

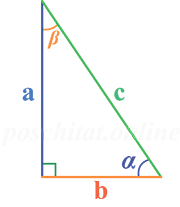
Чтобы найти острые углы прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):

• для угла α:
• угол β
• длины катетов a и b
• длину гипотенузы (с) и длину одного из катетов
• для угла β:
• угол α
• длины катетов a и b
• длину гипотенузы (с) и длину одного из катетов

Введите их в соответствующие поля и получите результат.

Найти угол α зная угол β и наоборот

Формула

α = 90° — β

β = 90° — α

Найти углы прямоугольного треугольника зная катеты

Чему равны острые углы (α и

β) прямоугольного треугольника если известны оба катета (a и b)?

Формулы

tg(α) = ^a/_b

tg(β) = ^b/_a

или так:

α = arctg(^a/_b)

β = arctg(^b/_a)

Пример

Для примера определим чему равны углы α и β в градусах если катет a = 5 см, а катет b = 2 см:

∠α = arctg(5/2) = arctg(2.5) ≈ 68.2°

∠β = arctg(2/5) = arctg(0.4) ≈ 21.8°

Найти углы прямоугольного треугольника по катету и гипотенузе

Чему равны острые углы (α и β) прямоугольного треугольника если известны гипотенуза c и один из катетов (

a или b)?

Формулы

sin(α) = ^a/_c

sin(β) = ^b/_c

cos(α) = ^b/_c

cos(β) = ^a/_c

или так:

α = arcsin(^a/_c) = arccos(^b/_c)

β = arcsin(^b/_c) = arccos(^a/_c)

Пример

Для примера определим чему равны углы α и β в градусах если гипотенуза c = 6 см, а катет b = 3 см:

∠α = arccos(3/6) = arccos(0.5) = 60°

∠β = arcsin(3/6) = arcsin(0.5) = 30°

См. также

Как узнать градус угла без транспортира — MOREREMONTA

1. Для того, чтобы узнать угол между двумя стенами делаем отметки на стенах на одинаковом расстоянии от угла (например 50 или 100 см от угла, чем больше, тем точнее). Обозначим это расстояние ‘a’. Дальше.

2. Дальше меряем расстояние между отметками (т.е диагональ угла) — обозначим ‘С’.

3. Потом расчёты —

Осталось рассчитать, сколько градусов в вашем угле по формуле: cos(γ) = (a 2 + a 2 – c 2 ) / (2 • a • a)

Получив cos(γ) угла, далее через функцию arccos узнаём сколько это будет в градусах: arccos (cos(γ)) = угол.

Т.е. по примеру это: (50 2 + 50 2 – 71,5 2 ) / (2 • 50 • 50) = -0,02245 отсюда arccos (-0,02245)= 91.28 градусов.

Здесь можно посчитать сразу!

Наш калькулятор:

Доступ к калькулятору платный!
На неделю — 37 р!

Что нужно сделать?
1. Зарегистрироваться — здесь!
2. Войти — здесь!
3. Пополнить счёт, кликнув по картинке (виза, master card, мобильные операторы) —

При отделочных работах и строительстве бывает нужна четкая геометрия: перпендикулярные стены и иные конструкции, требующие прямого угла в 90 градусов. Обыкновенный угольник не может позволить проверить или разметить углы со сторонами в несколько метров. Описываемый же метод превосходно подходит для разметки или проверки любых углов — длинна сторон не ограничена. Основной инструмент для измерений — рулетка.

Мы будем рассматривать точную разметку прямого угла, а также метод проверки уже размеченных углов на стенах и других объектах.

Теорема Пифагора

Теорема основана на утверждении, что у прямоугольного треугольника сумма квадратов длин катетов равна квадрату длины гипотенузы. В виде формулы записывается это так:

Стороны a и b — катеты, между которыми угол равен ровно 90 градусов. Следовательно, сторона c — гипотенуза. Подставляя в эту формулу две известные величины, мы можем вычислить третью, неизвестную. А следовательно можем размечать прямые углы, а также проверять их.

Теорема Пифагора известна еще под названием «египетский треугольник». Это треугольник со сторонами 3, 4 и 5, причем совершенно не важно, в каких единицах длинны. Между сторонами 3 и 4 — ровно девяносто градусов. Проверим данное утверждение вышеприведенной формулой: a²+b²=c² = (3×3)+(4×4) = 9+16 = (5×5) = 25 — все сходится!

А теперь применим теорему на практике.

Проверка прямого угла

Начнем с самого простого — проверки прямого угла с помощью теоремы Пифагора. Самым частым примером в отделке и строительстве является проверка перпендикулярности стен. Перпендикулярные стены — это стены, расположенные друг к другу под прямым углом 90°.

Итак, берем любой проверяемый внутренний угол. На стенах (на одной высоте) или на полу отмечаем на обоих стенах отрезки произвольных длин. Длинна этих отрезков произвольная, по возможности нужно отмечать как можно больше, но чтобы между отметками на стенах удобно было мерить диагональ. Например, мы отметили 2,5 метра (или 250 см.) на одной стене и 3 метра (или 300 см.) на другой. Теперь длину отрезка каждой стены возводим в квадрат (умножаем саму на себя) и получившиеся произведения складываем. Выглядит это так: (2,5×2,5)+(3×3)=15,25 — это диагональ в квадрате. Теперь нужно извлечь из этого числа квадратный корень √15,25≈3,90 — 3,9 метра должна составлять диагональ между нашими отметками. Если измерение рулеткой показывает другую длину диагонали — проверяемый угол развернут и имеет отклонение от 90°.

Калькулятор расчета диагонали прямого угла

Извлечение квадратного корня никогда меня не привлекало — простому человеку не обойтись без калькулятора, к тому же, не на всех мобильных устройствах калькуляторы умеют извлекать его. Поэтому можно пользоваться упрощенным методом. Нужно лишь запомнить: у прямого угла со сторонами ровно 100 сантиметров, диагональ равна 141,4 см. Таким образом, у прямого угла со сторонами 2 м. — диагональ равна 282,8 см. То есть на каждый метр плоскости приходится 141,4 см. У этого метода один недостаток: от измеряемого угла нужно откладывать одинаковые расстояния на обеих стенах и отрезки эти должны быть кратны метру. Не буду утверждать, но по моей скромной практике — это гораздо удобнее. Хотя не стоит забывать о первоначальном способе совсем — в некоторых случаях он очень актуален.

Сразу же возникает вопрос: какое отклонение от вычисленной длинны диагонали считать нормой (погрешностью), а какое нет? Если проверяемый угол с отмеченными сторонами по 1 м. будет 89°, то диагональ уменьшится до 140 см. Из понимания этой зависимости можно сделать объективный вывод, что погрешность диагонали 141,4 см. в несколько миллиметров не даст отклонения в один целый градус.

Как проверить внешний угол? Проверка внешнего угла по сути не отличается, нужно лишь продлить линии каждой стены на полу (или земле, при помощи шнура) и получившийся внутренний угол измерить обычным способом.

Как разметить прямой угол рулеткой

Разметка может основываться как на общей теореме Пифагора, так и на принципе «египетского треугольника». Однако это только в теории линии просто чертятся на бумаге, «ловить» же все выбранные размеры растянутыми шнурами или линиями на полу — задача посложнее.

Поэтому я предлагаю упрощенный способ, основанный на диагонали 141,4 см. у треугольника со сторонами 100 см. Вся последовательность разметки изображена на картинках ниже. Важно не забывать: диагональ 141,4 см. нужно умножать на количество метров в отрезке А-Б. Отрезки А-Б и А-В должны быть равны и соответствовать целому числу в метрах. Картинки увеличиваются по клику!

Как разметить острый угол

Гораздо реже возникает надобность в создании острых углов, в частности 45°. Для формирования подобных фигур формулы более сложные, однако это не самое проблематичное. Гораздо сложнее свести все линии, начерченные или натянутые шнурами — дело это непростое. Поэтому я предлагаю использовать упрощенный метод. Сначала размечается прямой угол 90°, а затем диагональ 141,4 делится на нужное количество равных частей. Например, чтобы получить 45°, диагональ нужно поделить пополам и от точки А провести линию через место деления. Таким образом мы получим два угла по 45 градусов. Если поделить диагональ на 3 части, то получится три угла по 30 градусов. Думаю алгоритм вам понятен.

Собственно я рассказал все, что мог рассказать, надеюсь все изложил понятным языком и у вас больше не возникнет вопросов как размечать и проверять прямые углы. Стоит добавить, что уметь делать это должен любой отделочник или строитель, ведь полагаться на строительный угольник небольшого размера — непрофессионально.

Измерить угол – значит найти его величину. Величина угла показывает, сколько раз угол, выбранный за единицу измерения, укладывается в данном углу.

Обычно за единицу измерения углов принимают градус. Градус – это угол, равный части развёрнутого угла. Для обозначения градусов в тексте, используется знак °, который ставится в правом верхнем углу числа, показывающего количество градусов (например, 60°).

Измерение углов транспортиром

Для измерения углов используют специальный прибор – транспортир:

У транспортира две шкалы – внутренняя и внешняя. Начало отсчёта у внутренней и у внешней шкал располагается с разных сторон. Чтобы получить правильный результат измерения, отсчёт градусов должен начинаться с правильной стороны.

Измерение углов производится следующим образом: транспортир накладывают на угол так, чтобы вершина угла совпала с центром транспортира, а одна из сторон угла прошла через нулевое деление на шкале. Тогда другая сторона угла укажет величину угла в градусах:

Говорят: угол BOC равен 60 градусов, угол MON равен 120 градусов и пишут: ∠BOC = 60°, ∠MON = 120°.

Для более точного измерения углов используют доли градуса: минуты и секунды. Минута – это угол, равный части градуса. Секунда – это угол, равный части минуты. Минуты обозначают знаком ‘, a секунды – знаком ». Знак минут и секунд ставится в правом верхнем углу числа. Например, если угол имеет величину 50 градусов 34 минуты и 19 секунд, то пишут:

Свойства измерения углов

Если луч делит данный угол на две части (на два угла), то величина данного угла равна сумме величин двух полученных углов.

Рассмотрим угол AOB:

Луч OD делит его на два угла: ∠AOD и ∠DOB. Таким образом, ∠AOB = ∠AOD + ∠DOB.

Развёрнутый угол равен 180°.

Любой угол имеет определённую величину, большую нуля.

Угловой размер, линейный размер и расстояние

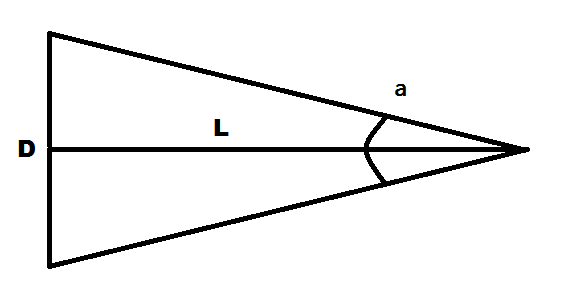
Угловой размер — это угол между линиями, соединяющими диаметрально противоположные точки измеряемого объекта и глаз наблюдателя.
Посмотрим на рисунок: здесь отрезок D — измеряемый объект, отрезок L — линия наблюдения, перпендикулярная отрезку D и являющаяся его серединным перпендикуляром, и угол а — угловой размер отрезка D.
Очевидные соотношения между величинами (вспомним тригонометрию):

Таким образом, наблюдатель, зная, например, линейный размер объекта, по угловому размеру объекта может определить расстояние до него. Помню, раньше для этих целей военные бинокли снабжали специальными риcками для определения углового размера.

Ну и обратные задачи тоже имеют место — зная, например, расстояние и линейный размер объекта, можно определить его угловой размер; и наконец, зная расстояние и угловой размер, можно определить линейный размер. Последние задачи актуальны для астрономии. Там используют термин угловой диаметр — то есть видимый диаметр небесного тела, выраженный в угловых мерах.

Ниже калькуляторы, рассчитывающие неизвестные по всем соотношениям. В качестве данных по умолчанию используется расстояние от Земли до Солнца, диаметр Солнца и средний угловой диаметр Солнца, наблюдаемого с Земли.

Расстояние по угловому и линейному размеру

Угловой размерТочность вычисления

Знаков после запятой: 2

save Сохранить share Поделиться extension Виджет

Линейный размер по угловому размеру и расстоянию

Угловой размерТочность вычисления

Знаков после запятой: 2

Линейный размер

 

save Сохранить share Поделиться extension Виджет

Угловой размер по расстоянию и линейному размеру

Угловой размер

 

save Сохранить share Поделиться extension Виджет

Градусная мера угла / Начальные геометрические сведения / Справочник по геометрии 7-9 класс

1. Главная
2. Справочники
3. Справочник по геометрии 7-9 класс
4. Начальные геометрические сведения
5. Градусная мера угла

Нам известно, что при измерении отрезков, мы сравниваем измеряемый отрезок с отрезком, который принят за единицу измерения. Аналогично происходит измерение углов: чтобы измерить угол его сравнивают с углом, который принят за единицу измерения —  с  градусом.

---

Градус — это угол, который равен 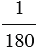части развернутого угла,обозначается знаком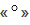

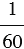часть градуса называется минутой, обозначается знаком

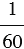часть минуты называется секундой, обозначается знаком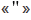

Пример: 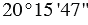(двадцать градусов пятнадцать минут сорок семь секунд)

Градусная мера угла — это положительное число, которое показывает, сколько раз градус и его части укладываются в данном угле.

Пример:

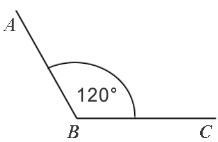
Градусная мера угла ABC равна 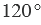. Говорят: «Угол ABC равен 120 градусам». Пишут: .

---

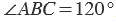Транспортир — это измерительный инструмент, который используется для измерения и построения углов. Состоит из линейки (прямолинейной шкалы) и полукруга (угломерной шкалы: внутренней и внешней), который разделен на градусы от 0 до .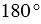

Для того чтобы измерить угол, необходимо совместить вершину угла с центром транспортира, при этом одна из сторон угла должна пройти через нулевое деление шкалы, тогда вторая сторона угла укажет градусную меру угла.

Пример: Измерим угол ABC, для этого совместим точку B с центром транспортира, и расположим транспортир так, чтобы сторона BC прошла через нулевое деление шкалы (обратите внимание отсчёт угла ведётся по той шкале, через нулевое деление которой пройдет одна из сторон угла: в нашем случае по внутренней шкале).

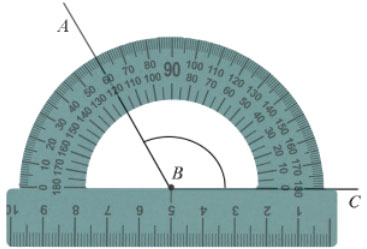
Вторая сторона при этом, как мы видим, проходит через деление шкалы 120, значит: .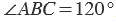

---

Свойства:

• Равные углы имеют равные градусные меры.
• Меньший угол имеет меньшую градусную меру.
• Развернутый угол равен .
• Неразвернутый угол меньше .
• Если луч делит угол на два угла, градусная мера всего угла равна сумме градусных мер этих углов.

---

Основные типы углов:

1. Острый угол — угол, градусная мера которого меньше 90°.

2. Прямой угол — угол, градусная мера которого равна 90°.

3. Тупой угол — угол, градусная мера которого больше 90°, но меньше 180°.

4. Развернутый угол — угол, градусная мера которого равна 180°.

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Точки, прямые, отрезки

Провешивание прямой на местности

Луч

Угол

Равенство геометрических фигур

Сравнение отрезков

Сравнение углов

Длина отрезка

Единицы измерения длины, расстояний

Измерение углов на местности

Смежные углы

Вертикальные углы

Перпендикулярные прямые

Построение прямых углов на местности

Начальные геометрические сведения

Правило встречается в следующих упражнениях:

7 класс

Задание 67, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 88, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 89, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 102, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 147, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 299, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 345, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 646, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 896, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

---

© budu5.com, 2020

Пользовательское соглашение

Copyright

Онлайн калькулятор: Калькулятор выражений с градусами

Этот калькулятор выполняет арифметические действия над градусами. Как и Арифметика двоичных чисел, технически он сделан на базе калькулятора Математический калькулятор. Сделан был по запросу пользователя Калькулятор .

Вводим выражение с градусами, калькулятор считает. Тонкость тут в форме ввода значений в градусах, ибо символ градуса как-то сложно набрать на клавиатуре. Собственно, вот примеры того, как вводить градусы с их интерпретацией калькулятором:

15 — 15 градусов 0 минут 0 секунд
15.3 — 15 градусов 18 минут 0 секунд (выражение интерпретируется как доли градуса)
15.3′ — 15 градусов 3 минуты 0 секунд (выражение интерпретируется как градусы/минуты)
15.3’5 — 15 градусов 3 минуты 5 секунд (выражение интерпретируется как градусы/минуты/секунды)
15.3’5′ — 15 градусов 3 минуты 5 секунд (выражение интерпретируется как градусы/минуты/секунды)
15.3’5» — 15 градусов 3 минуты 5 секунд (выражение интерпретируется как градусы/минуты/секунды)
15.3.5 — 15 градусов 3 минуты 5 секунд (выражение интерпретируется как градусы/минуты/секунды)
.3 — 0 градусов 18 минут 0 секунд (выражение интерпретируется как доли градуса)
.3′ — 0 градусов 3 минуты 0 секунд (выражение интерпретируется как градусы/минуты/секунды)
.3.5 — 0 градусов 3 минуты 5 секунд (выражение интерпретируется как градусы/минуты/секунды)
.3’5 — 0 градусов 3 минуты 5 секунд (выражение интерпретируется как градусы/минуты/секунды)
.3’5′ — 0 градусов 3 минуты 5 секунд (выражение интерпретируется как градусы/минуты/секунды)
.3’5» — 0 градусов 3 минуты 5 секунд (выражение интерпретируется как градусы/минуты/секунды)

Несколько вариантов записи, чтобы кому как удобнее было.

Калькулятор действий над градусами

Точность вычисления

Знаков после запятой: 2

Результат вычисления (градусы/минуты/секунды)

 

Результат вычисления (доли градуса)

 

save Сохранить share Поделиться extension Виджет

Как с помощью одной рулетки проверить градус углов в помещении

Одним из основных признаков качественно проведения ремонтных работ является хорошая геометрия помещения. Поэтому очень важно вымерять все выводимые углы, чтобы добиться максимально презентабельного конечного результата. К тому ж, отделочные работы и этап строительства требует перпендикулярного размещения стен по отношению к полу или к различным конструкциям.

Обычный угольник не поможет выявить отклонения или вывести углы, которые имели бы стороны в несколько метров. Но не стоит сразу же срывать с места и искать специальный прибор для этих целей. Выявить все отклонения помогут обычные инструменты, которые можно найти в любом дома – рулетка и карандаш.

Как пользоваться рулеткой для измерения углов?

Для этого не потребуется приобретать серьезные покупки и инструменты – достаточно иметь под рукой карандаш и обычную рулетку. Еще понадобятся обычные вещи, которые есть в домашнем обиходе у любой хозяйки. Если их нет, то всегда есть возможность приобрести в магазине. Здесь не должно возникнуть никаких трудностей.

Чтобы вычислить угол с помощью рулетки, придется воспользоваться принципом «3-4-5». Он поможет определить угол в 90 градусов. Все, что потребуется, это немного подумать и вникнуть в расчеты.

Важно! Во время возведения здания точность углов должна соблюдаться в обязательном порядке.

Итак, процедура проверки базируется на следующих шагах:

• Начала необходимо понять, почему принцип называется «3-4-5» и вспомнить школьную геометрию. Цифры не являются обычным набором – это величины сторон треугольника. Чтобы вникнуть в суть, нужно вспомнить теорему Пифагора, где сумма квадратов катета равна квадрату гипотенузы. Данные числа отлично подходят для ее проверки: 32+42=52. Показания будут использоваться в дальнейшем.
• Отмерить от угла три метра вдоль прилегающей стены. Здесь важно отметить, что три метра является предпочтительной длинной. Если же комната не обладает большими габаритами, то достаточно просто отмерять 30 сантиметров.
• Можно использовать любые другие цифры только главное, чтобы они были пропорционально увеличенными.
• После этого, отмерить четыре метра на другой стене соответственно начинать с угла. Или же 40 сантиметров. Делается отметка.
• Завершающий этап, который позволит понять прямой ли угол или нет. От отметины на двух стенах проводиться линия, которая будет являться гипотенузой. Это расстояние необходимо замерить. Полученные данные, помогут сделать определенный вывод.

В случае, когда расстояние между отметками будет равно 5 метрам или 50 сантиметрам, для маленьких габаритов комнаты, то угол равен 90 градусам. Данный показатель говорит о том, что он прямой.

Если же полученное значение меньше 5 метров, значит, что угол намного меньше, чем 90 градусов. Величина, которая больше 5 метров, указывает на тупой угол свыше 90 градусов.

Вот такой простой и быстрый способ поможет проверить все углы в помещении, при этом не потребуется использование каких-либо дорогостоящих специальных инструментов.