Как угол 90 градусов вымерить: Как высчитать угол 90 градусов рулеткой

Содержание

Как высчитать угол 90 градусов рулеткой

При отделочных работах и строительстве бывает нужна четкая геометрия: перпендикулярные стены и иные конструкции, требующие прямого угла в 90 градусов. Обыкновенный угольник не может позволить проверить или разметить углы со сторонами в несколько метров. Описываемый же метод превосходно подходит для разметки или проверки любых углов — длинна сторон не ограничена. Основной инструмент для измерений — рулетка.

Мы будем рассматривать точную разметку прямого угла, а также метод проверки уже размеченных углов на стенах и других объектах.

Теорема Пифагора

Теорема основана на утверждении, что у прямоугольного треугольника сумма квадратов длин катетов равна квадрату длины гипотенузы. В виде формулы записывается это так:

Стороны a и b — катеты, между которыми угол равен ровно 90 градусов. Следовательно, сторона c — гипотенуза. Подставляя в эту формулу две известные величины, мы можем вычислить третью, неизвестную.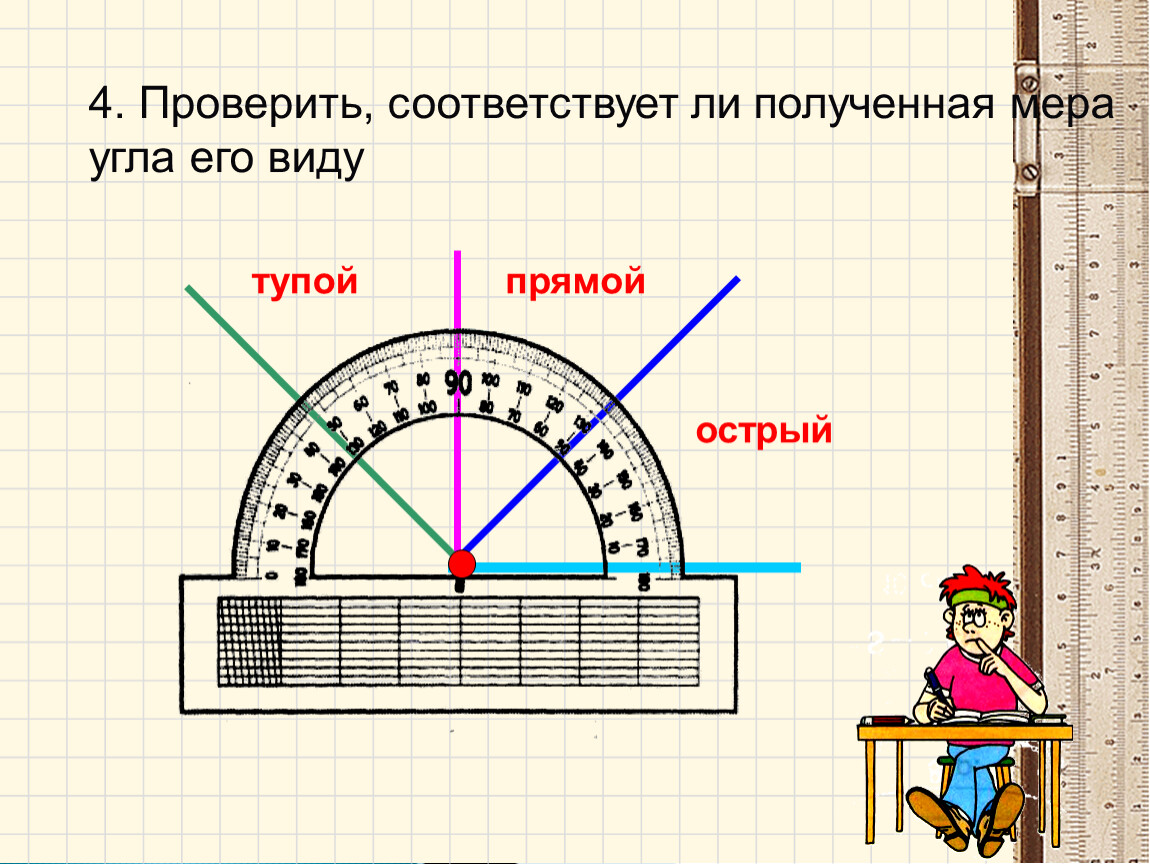

А следовательно можем размечать прямые углы, а также проверять их.

Теорема Пифагора известна еще под названием «египетский треугольник». Это треугольник со сторонами 3, 4 и 5, причем совершенно не важно, в каких единицах длинны. Между сторонами 3 и 4 — ровно девяносто градусов. Проверим данное утверждение вышеприведенной формулой: a²+b²=c² = (3×3)+(4×4) = 9+16 = (5×5) = 25 — все сходится!

А теперь применим теорему на практике.

Проверка прямого угла

Начнем с самого простого — проверки прямого угла с помощью теоремы Пифагора. Самым частым примером в отделке и строительстве является проверка перпендикулярности стен. Перпендикулярные стены — это стены, расположенные друг к другу под прямым углом 90°.

Итак, берем любой проверяемый внутренний угол. На стенах (на одной высоте) или на полу отмечаем на обоих стенах отрезки произвольных длин. Длинна этих отрезков произвольная, по возможности нужно отмечать как можно больше, но чтобы между отметками на стенах удобно было мерить диагональ. Например, мы отметили 2,5 метра (или 250 см.) на одной стене и 3 метра (или 300 см.) на другой. Теперь длину отрезка каждой стены возводим в квадрат (умножаем саму на себя) и получившиеся произведения складываем. Выглядит это так: (2,5×2,5)+(3×3)=15,25 — это диагональ в квадрате. Теперь нужно извлечь из этого числа квадратный корень √15,25≈3,90 — 3,9 метра должна составлять диагональ между нашими отметками. Если измерение рулеткой показывает другую длину диагонали — проверяемый угол развернут и имеет отклонение от 90°.

Калькулятор расчета диагонали прямого угла

Извлечение квадратного корня никогда меня не привлекало — простому человеку не обойтись без калькулятора, к тому же, не на всех мобильных устройствах калькуляторы умеют извлекать его. Поэтому можно пользоваться упрощенным методом. Нужно лишь запомнить: у прямого угла со сторонами ровно 100 сантиметров, диагональ равна 141,4 см. Таким образом, у прямого угла со сторонами 2 м. — диагональ равна 282,8 см.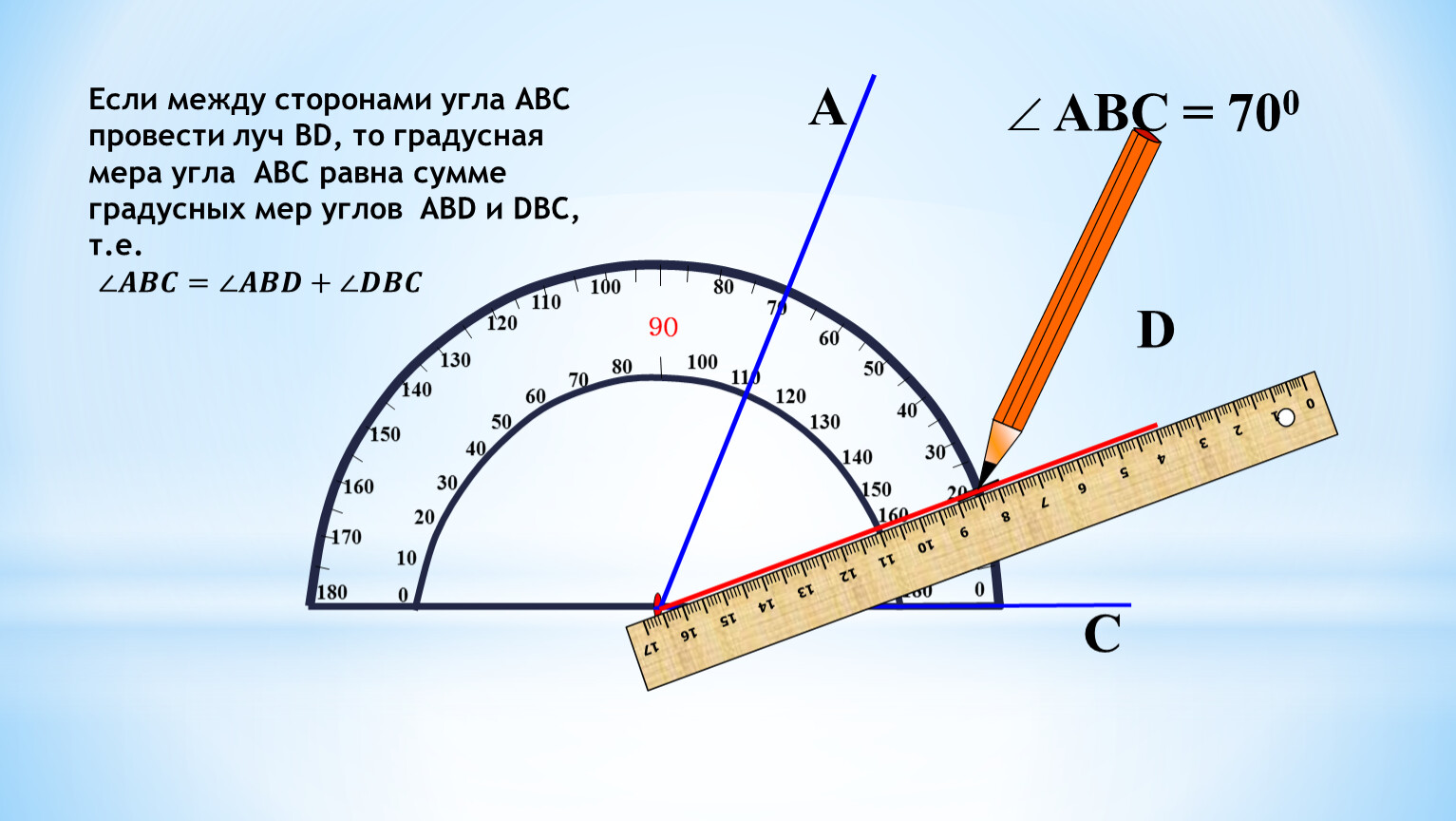

То есть на каждый метр плоскости приходится 141,4 см. У этого метода один недостаток: от измеряемого угла нужно откладывать одинаковые расстояния на обеих стенах и отрезки эти должны быть кратны метру. Не буду утверждать, но по моей скромной практике — это гораздо удобнее. Хотя не стоит забывать о первоначальном способе совсем — в некоторых случаях он очень актуален.

Сразу же возникает вопрос: какое отклонение от вычисленной длинны диагонали считать нормой (погрешностью), а какое нет? Если проверяемый угол с отмеченными сторонами по 1 м. будет 89°, то диагональ уменьшится до 140 см. Из понимания этой зависимости можно сделать объективный вывод, что погрешность диагонали 141,4 см. в несколько миллиметров не даст отклонения в один целый градус.

Как проверить внешний угол? Проверка внешнего угла по сути не отличается, нужно лишь продлить линии каждой стены на полу (или земле, при помощи шнура) и получившийся внутренний угол измерить обычным способом.

Как разметить прямой угол рулеткой

Разметка может основываться как на общей теореме Пифагора, так и на принципе «египетского треугольника». Однако это только в теории линии просто чертятся на бумаге, «ловить» же все выбранные размеры растянутыми шнурами или линиями на полу — задача посложнее.

Поэтому я предлагаю упрощенный способ, основанный на диагонали 141,4 см. у треугольника со сторонами 100 см. Вся последовательность разметки изображена на картинках ниже. Важно не забывать: диагональ 141,4 см. нужно умножать на количество метров в отрезке А-Б. Отрезки А-Б и А-В должны быть равны и соответствовать целому числу в метрах. Картинки увеличиваются по клику!

Как разметить острый угол

Гораздо реже возникает надобность в создании острых углов, в частности 45°. Для формирования подобных фигур формулы более сложные, однако это не самое проблематичное. Гораздо сложнее свести все линии, начерченные или натянутые шнурами — дело это непростое. Поэтому я предлагаю использовать упрощенный метод. Сначала размечается прямой угол 90°, а затем диагональ 141,4 делится на нужное количество равных частей. Например, чтобы получить 45°, диагональ нужно поделить пополам и от точки А провести линию через место деления.

Таким образом мы получим два угла по 45 градусов. Если поделить диагональ на 3 части, то получится три угла по 30 градусов. Думаю алгоритм вам понятен.

Собственно я рассказал все, что мог рассказать, надеюсь все изложил понятным языком и у вас больше не возникнет вопросов как размечать и проверять прямые углы. Стоит добавить, что уметь делать это должен любой отделочник или строитель, ведь полагаться на строительный угольник небольшого размера — непрофессионально.

При ремонте, строительстве или самостоятельном изготовлении мебели часто бывает необходимо проверить или построить прямой угол. В любом случае, очень важна точность измерения, но если стороны угла равны нескольким метрам, то это сложно будет сделать с помощью угольника. Сегодня мы рассмотрим несколько универсальных методов замера прямого угла с помощью рулетки.

Теорема Пифагора

Проверить прямой угол поможет известная каждому со школьных времен теорема Пифагора. Вспомним определение: ”В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов” ( a 2 + b 2

= с 2 ), где a и b – катеты, а с – гипотенуза.

Подставив в формулу известные нам две величины, получим неизвестную третью.

А теперь вернемся к нашим замерам и применим теорему на практике.

Для того, чтобы проверить угол, отмечаем на обеих стенах произвольные отрезки, желательно отмерять их побольше, чтобы удобнее было отмерять диагональ между ними. После того, как вы отметили эти отрезки, возведите длину каждого в квадрат и сложите. Из полученного результата извлеките квадратный корень (для удобства можно воспользоваться калькулятором). Теперь замеряем рулеткой длину диагонали между двумя отрезками, она должна совпадать с полученным результатом. Если в результате измерения получилось другое число, то угол не равен 90 градусов.

Египетский треугольник

Также не стоит забывать и о такой геометрической фигуре, как египетский треугольник – прямоугольник с длинами сторон 3, 4, 5, причем совершенно не важно в каких величинах, ведь между катетами длиной 3 и 4 угол, равный ровно 90 градусов. Давайте проверим?

a 2 + b 2 = (3 2 + 4 2 ) = (9 + 16) = 25; √25 = 5.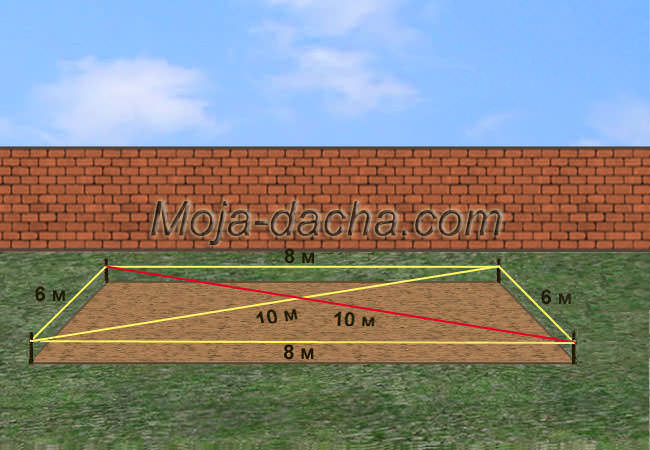

Как проверить угол с помощью египетского треугольника?

Отмерьте на одной стене отрезок длиной 3 метра, а на другой – отрезок длиной 4 метра. Теперь измеряем расстояние между двумя этими отметками точно так же, как в способе с теоремой Пифагора. Если получившийся результат кратен 5, то в том, что полученный угол равен 90 градусов, можно не сомневаться.

Как отмерить угол, используя рулетку

Можно самостоятельно смастерить угольник для замера углов:

Соединяем две рейки одна перпендикулярно другой.
Измеряем на одной рейке 60 см, на другой 80, лишнее обрезаем.
Прибиваем третью рейку к одной отметке.
Измеряем гипотенузу, прибиваем рейку ко второй метке.
Еще раз проверяем размеры и при необходимости фиксируем ещё в нескольких местах.
Обрезаем лишние концы.

Как видите, знание нескольких простых школьных теорем может помочь и в строительстве, и в ремонте. Зная несколько простых хитростей, вы всегда с легкостью можете создать или проверить прямой угол.

Строительная рулетка для электрика является таким же обязательным инструментом, как и индикатор напряжения. Даже у тех профессионалов, которые имеют в комплекте инструмента осепостроители и лазерные дальномеры, непременно в подсумке всегда присутствует обыкновенная рулетка.

Без нее не обойтись ни при разметке трасс электропроводки, ни при монтаже подрозетников.
Однако далеко не каждый знаком со всеми секретами и дополнительными возможностями при использовании строительной рулетки.

У нее оказывается очень много скрытых способностей, которые помогут вам заменить сразу несколько инструментов и значительно сэкономить время на ремонт.

Кстати, один из важных советов, для тех кто пользуется китайскими дешевыми рулетками заключается в следующем — если у вас именно такой экземпляр, то старайтесь все замеры делать одной рулеткой.

Один и тот же размер при измерении разными рулетками может не совпадать.

Один знакомый измерял расстояние стен в доме китайским инструментом, а в магазине при покупке материалов воспользовался их рулеткой. В итоге, дома очень был удивлен результатом покупки.

Подвижный зацеп сегодня встречается почти на каждой рулетке. И эта штука вовсе не для того, чтобы удобно спину почесать 🙂
Новички вообще нередко думают, что это какой-то брак. Какая в итоге будет точность, если один из ключевых элементов болтается и не закреплен надежно? Некоторые даже умудряются его заклепать сразу же после покупки.

Оказывается, что подвижный зацеп это необходимость, без которой вообще не возможна нормальная работа.
Объясняется это тем, что измерения рулеткой можно производить двумя способами:

от предмета

Когда вы измеряете расстояние от предмета, зацеп выполняет роль нулевой точки. При измерении с захватом предмета, зацеп выдвигается на свою толщину. Тем самым нулевая отметка снова совпадает с краем предмета.

Поэтому не стоит сматывать строительную рулетку с эффектным щелчком в конце, тем самым вы только сократите срок ее службы.

Еще во многих моделях лента рулетки в самом начале на расстоянии 2,5см имеет отверстие. Сделано оно не просто так, а опять же чтобы облегчить вашу работу в одиночку.
Когда не за что закрепиться зацепом или неудобно им пользоваться из-за косой поверхности, простым шилом или гвоздиком через отверстие намертво закрепляете ленту и растягиваете ее на любую длину.

Воспользовавшись таким отверстием в рулетке вам не придется применять подобные захваты как на фото ниже. А всю работу по разметке можно легко проделывать без напарника.

Как вы понимаете при замерах в углах, серединой ленты рулетки очень трудно залезть непосредственно в угол. Также неудобно делать точные измерения в дверном или оконном проеме.
Поэтому в том случае когда нужно замерить проем, используйте корпус как продолжение рулетки.

На внешней стороне самой рулетки указан размер корпуса, который и нужно прибавить к показаниям ленты при измерении.

Если такого размера на корпус не нанесено, никто вам не мешает самостоятельно его измерить и написать в любом удобном месте.

Есть еще способ сделать подобные замеры с применением малярной ленты. Наклеиваете на поверхность кусочек ленты и производите два измерения в противоположных направлениях.

При этом карандашом в качестве метки лучше ставить галочки, а не простые черточки. Они будут визуально точнее показывать отметку. Тогда как черточка может быть нарисована криво, что и вызовет погрешность.

Проделав два измерения нужно сложить результаты и получите точный размер.

На многих зацепах рулетка имеет небольшое отверстие. Этим отверстием удобно зацепиться за шуруп или гвоздь. После этого зацеп уже никуда не соскочит.

Особенно это полезно, когда вы в одиночку проводите измерения на больших расстояниях. Погрешность измерения при этом будет не более 1-2мм, так как центр шурупа находится практически на нулевой отметке ленты.

Еще при помощи этого разъема в зацепе очень удобно рисовать окружности. Не нужно при себе иметь ни циркуля, ни транспортира.

В некоторых моделях зацепы выполняют магнитными. Помимо прямого их назначения, такими зацепами удобно поднимать упавшие предметы не слезая со стремянки.

Если применить небольшую доработку к дешевой рулетке, то из одного инструмента получается отличное приспособление для разметки.
Берете ножку циркуля, которая применяется с простыми карандашами, и закрепляете ее на внешней стороне рулетки.

Эту конструкцию можно сделать съемной, или вообще приспособить под отдельную рулетку.

Таким устройством очень удобно делать различные отметки или пользоваться им как рейсмусом.

А при использовании шурупа легко рисуются окружности нужного диаметра.

Если вы работаете с гипсокартоном или другой поверхностью, которую можно безопасно поцарапать, то рулетку стоит переделать под еще одну возможность. Надфилем на зацепе делаете зазубрины.

После чего с помощью этого зацепа легко делаются отметки на поверхности. При этом уже даже не обязательно чтобы под рукой был карандаш.

Внешнюю часть рулетки легко превратить в мини напоминалку или поверхность для записей. Берете малярную ленту и наклеиваете сбоку рулетки.

Если нет под рукой малярки, то можно писать прямо на самом корпусе.
Правда для этого, сначала надо пройтись по поверхности наждачкой нулевкой.

Так вы сделаете ее несколько бархатной, после чего надписи будут наноситься горазд легче.

Писать конечно нужно карандашом, после чего все это легко стирается резинкой.

С помощью строительной рулетки очень легко разделить любое число с точность до миллиметра пополам, не прибегая к услугам калькулятора.

Берете размер на рулетке, к примеру 116см — и сложив ленту пополам совмещаете с ним нулевую отметку, там где верхний зацеп.

Ровно в месте перегиба и будет требуемый результат — 58см.

Этим же способом можно не только делить, но и отнимать. Например общая длина стенки у вас 2м 11см, а распредкоробка находится от первого края на расстоянии в 1м 38см. Вам нужно быстро узнать сколько остается от этой распредкоробки до другого края стены, чтобы отмерить кабель канал.

Вытягиваете ленту на 2м 11см и складываете ее пополам.

Затем ищете отметку в 1м 38см. Как раз напротив нее, на второй половине ленты, и будет показано нужное вам расстояние — 73см.

Используя обыкновенную ленту рулетки можно легко разделить рабочую поверхность или заготовку на требуемое количество равных частей. Данный метод подходит в первую очередь для больших поверхностей — для труб или кабель каналов уже не сработает.

Как вы поступаете обычно? Замеряете общую длину или ширину, затем делаете вычисления и делите расстояние на нужное количество частей. После чего вновь линейкой или рулеткой отмеряете на поверхности эти части.

Оказывается все это можно проделать без калькулятора и даже без вычислений. Берете на рулетке число, которое больше чем ширина заготовки, и при этом кратно той величине, на которое вы хотите разделить расстояние.

Например ширина доски 17см, а вам ее нужно разделить на четыре равные части. Сдвигаете рулетку по диагонали до ближайшей отметки в 20см. После чего легко делите эти 20см на 4 и отмечаете метки на расстояниях 5см, 10см, 15см, 20см.

В итоге вы всего одним движением рулетки разделили поверхность на нужное количество частей.

Захотели поделить на 6 частей — ничего сложного. Можно сдвинуть диагональ до 30см и проделать то же самое.

Еще рулеткой на круглой трубе можно точно отмерить поперечный срез. Для этого плотно прижимаете по периметру трубы ленту, совместив концы. Если совместили ровно, никак иначе как под углом в 90 градусов она не ляжет.

Чем шире лента рулетки, тем предпочтительней. Проделать такой же фокус можно и с простым листком бумаги.

Когда невозможно измерить диаметр трубы или заготовки с торца, опять поможет строительная рулетка и геометрия. Обхватываете трубу лентой и измеряете ее окружность. После чего полученный результат нужно разделить на число Пи = 3,14. Это и будет необходимый диаметр.

Еще раз применив знания геометрии, строительной рулеткой без угольников и других инструментов можно проверить точность прямого угла. Как вы знаете из школьного курса — сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы.

Берете любую поверхность где должен быть прямой угол, например две стены комнаты. Отмеряете рулеткой в одну сторону 30см, а в другую 40см и ставите метки. Если угол действительно прямой и строители не накосячили, то соединив эти две метки по гипотенузе, вы должны получить на рулетке расстояние ровно в 50см.

Такой метод применим к любым поверхностям и изделиям. Главное что вам нужно соблюдать при измерении — это пропорции 3 -4 -5.

Если вы еще не приобрели себе рулетку, подобрать необходимую модель и ознакомиться с текущими ценами на них можно здесь.

Египетский треугольник. Прямой угол без инструмента. |

15.01.2016 profipol_dp 3 710 просмотра

Как выставить угол 90 градусов без специального инструмента (угольника)?

Допустим, у нас есть линия к которой нам нужно выставить перпендикуляр, т. е. еще одну линию под углом 90 градусов относительно первой. Или у нас есть угол (например, угол комнаты) и нам нужно проверить равен ли он 90 градусам.

Все это можно сделать с помощью одной только рулетки и карандаша.

Есть две отличные штуки, такие как «Египетский треугольник» и теорема Пифагора, которые нам в этом помогут.

Итак, Египетский треугольник — это прямоугольный треугольник с соотношением всех сторон равным 3:4:5 (катет 3: катет 4: гипотенуза 5).

Египетский треугольник напрямую связан с теоремой Пифагора — сумма квадратов катетов равна квадрату гипотенузы (3*3 + 4*4 = 5*5).

Как нам это может помочь? Все очень просто.

Задача №1. Нужно построить перпендикуляр к прямой линии (например, линию под 90 градусов к стене).

Шаг 1. Для этого от точки №1 (где будет наш угол) нужно отмерить на этой линии любое расстояние кратное трем или четырем — это будет наш первый катет (равный трем или четырем частям, соответственно), получаем точку №2.

Для простоты вычислений можно взять расстояние, например 2м (это 4 части по 50см).

Шаг 2. Затем от этой же точки №1 отмеряем 1,5м (3 части по 50см) вверх (выставляем примерный перпендикуляр), чертим линию (зеленая).

Шаг 3. Теперь из точки №2 нужно поставить метку на зеленой линии на расстоянии 2,5м (5 частей по 50см). Пересечение этих меток и будет нашей точкой №3.

Соединив точки №1 и №3 мы получим линию-перпендикуляр нашей первой линии.

Задача №2. Вторая ситуация — есть угол и нужно проверить прямой ли он.

Вот он, наш угол. Крнечно проще проверить большим угольником. А если его нет?

Отмеряем от угла любую длину кратную четырем, в данном случае это 1,6м.

В другую сторону три части, соответственно 1,2м.

И между этими точками должно оказаться пять частей, т.е. 2м.

Как видите, у нас угол оказался прямее всех прямых.

Чего и вам желаем!

Это тоже интересно:

инструмент, разметка укладки кафеля,

Самый простой способ как можно вычислить прямой угол подручными средствами

Каждый из нас учился в школе. Там человек получает огромное количество тех знаний, которые впоследствии могут понадобиться в жизни. Не все, конечно, могут в полной мере оценить значимость полученных знаний в школьной время, но сейчас речь не об этом.

Математика. Это страшное для многих слово, которое пугало достаточное количество школьников в своё время. Цифры, формулы и расчёты поддавались только самым пытливым. И с каждым годом этот сложный предмет становился всё сложнее и сложнее.

В старших классах появляется геометрия и всё становится ещё сложнее и непонятнее. Возможно, многие хоть раз в жизни, но в сердцах проклинали непонятную им науку и задавались вопросом, зачем это вообще нужно, и понадобится ли это в жизни.

Возможно, в повседневной жизни применить полученные в школе знания не удавалось. Вряд ли требовалось посреди белого дня высчитывать логарифмы и квадратные уравнения или доказывать, что две параллельные никогда не сойдутся. Но, где уж точно могут понадобиться знания геометрии и математике, так это в строительстве и при осуществлении ремонта.

В данной статье речь пойдёт о вычислении прямого угла, что требуется при строительстве зданий. Точность при возведении строений должна быть соблюдена в обязательном порядке, ведь только точные расчёты могут избавить от перекосов и нестабильности организации всего здания. Вычисление прямого угла при строительстве — не такой уж и трудный процесс, при котором потребуется знание и применение некоторых простых правил математики и геометрии. Подробнее об этом будет рассказано ниже.

Действительно ли прямой угол?

Возможно, некоторые читатели, ознакомившиеся с заголовком данной статьи, возразят, что прямой угол можно получить не всегда, и не всегда при строительстве используются именно ровные и точные прямые углы.

И, в принципе, они правы. Получить его весьма сложно, особенно если наблюдается неровность фундамента, на котором осуществляется строительство здания. Но, даже учитывая это обстоятельство, ни в коем случае нельзя делать вывод, что расчёт прямого угла можно делать просто «на глаз». В любом случае, если не представляется возможным вычислить идеальный прямой угол, то требуется достичь наиболее приближённого значения к идеальному углу в 90 градусов. И этого можно добиться, используя незатейливые инструменты и не самые сложные математические знания и познания в геометрии.

Что понадобится для определения прямого угла?

Итак, какие инструменты понадобится использовать для того, чтобы проверить прямой угол. Сразу стоит отметить, что никаких приборов и серьёзных инструментов для этого не потребуется. Нужно будет использовать весьма простые вещи, которые могут найтись практически в каждом хозяйстве. И даже если их не имеется под рукой, их с лёгкостью можно приобрести в магазине. С этим никаких трудностей не возникнет.

Для вычисления прямого угла нужно взять:

Карандаш;
Строительную рулетку.

И всё. Вот так вот всё просто.

Как можно вычислить прямой угол?

Итак, в этой статье будет описан принцип 3-4-5 при определении угла в 90 градусов. Ничего сложного в этом нет. Потребуется просто лишь чуть пораскинуть мозгами и вникнуть во все расчёты, которые смогут помочь в проверке угла.

Итак, нужно обозначить следующие шаги:

Для начала стоит разобраться в том, почему принцип так обозначен — 3-4-5. Это не просто набор цифр, это величина сторон прямоугольного треугольника. Теорема Пифагора гласит: квадрат гипотенузы равен сумме квадратов катетов. Цифры 3-4-5 очень подходят для проверки этого простого правила геометрии: 3*3+4*4=5*5, то есть 9+16=25. Именно эти цифры и будут использоваться в дальнейших вычислениях;
Итак, потребуется для начала отмерить 3 метра от угла вдоль одной из стен. Тут следует отметить, что 3 метра — предпочтительная длина замера, но в том случае, если комната маленькая, можно отметить всего 30 сантиметров. В месте замера нужно сделать отметку;
В принципе, можно использовать и другие цифры, но рекомендуется в любом случае использовать пропорционально увеличенные числа, например: 9-12-15 или же 30-40-50;
После проделанного предварительного замера нужно отмерить 4 метра вдоль другой стены, тоже от угла. Ну или соответственно 40 сантиметров, если комната маленькая. Нужно сделать отметку;
Теперь остаётся сделать последнее действие, по которому уже можно судить прямой угол или нет. От измеряющего потребуется измерить расстояние между сделанными отметками. По полученным данным можно будет сделать определённые выводы:
- Если расстояние между отметками будет равняться 5 метрам ровно, это будет означать, что угол является прямым;
- В том случае, если измеренное расстояние будет равняться меньше 5 метров, угол будет меньше, чем 90 градусов;
- Ну и, наконец, величина угла будет составлять больше 90 градусов, если полученная величина замера будет равняться больше 5 метров.

Вывод

Вот, как просто можно вычислить прямой угол без использования каких-либо строительных инструментов и приборов. Использовать можно самое простое, но в то же время весьма действенное средство, которое вкупе с использованием имеющихся знаний и бесхитростных расчётов, может помочь произвести измерение.

При использовании предложенных величин, ключевым становится финальный замер между двумя отметками, которые были сделаны ранее. Расстояние, которое будет равняться точно 5 метрам, покажется, что он прямой. Если же величина будет больше или меньше 5 метров, это будет означать, что он прямым не является.

Как измерить углы с помощью теодолита — Вокруг-Дом

Теодолит — это инструмент, обычно используемый строителями и инженерами для измерения точных углов, что необходимо для крупномасштабных строительных проектов. Базовый современный оптический теодолит обычно состоит из небольшого телескопа, который соединен с двумя механизмами измерения углов, один для измерения горизонтальных углов и один для измерения вертикальных углов. Он расположен на вращающейся подставке с механизмом выравнивания на штативе. Как только теодолит установлен, телескоп поворачивается, чтобы определить желаемую точку, и затем угол от точки, в которой теодолит находится до точки, замеченной в его телескопе, может быть считан через окуляр прицела.

кредит: Jupiterimages / Photos.com / Getty Images

Установка теодолита

Шаг 1

Найдите участок твердой ровной площадки с хорошим обзором того, что вы хотите заметить.

Шаг 2

Вытяните ножки штатива, чтобы теодолит находился на удобном для вас уровне, распрямите их до упора (большинство теодолитовых штативов имеют механизм, который блокирует их, когда они достигают максимального разделения и расширения) и воткните концы ног в землю как можно больше.

Шаг 3

Отрегулируйте три выравнивающих винта на основании теодолита так, чтобы он был ровным. Сферический спиртовой уровень, установленный на теодолите, даст вам представление о том, когда он приблизительно равен уровню.

Шаг 4

Совместите длинный спиртовой уровень с двумя из трех винтов и перенастройте эти два винта, чтобы добиться более точного уровня на этой оси. Затем поверните теодолит на 90 градусов и снова отрегулируйте его с помощью третьего винта.

Шаг 5

Освободите два горизонтальных зажима регулятора (обычно большие ручки с обеих сторон теодолита, слегка смещенные по вертикали).

Шаг 6

Совместите верхнюю часть теодолита с отметкой на кольце между двумя сторонами, которые соединены с горизонтальными зажимами, затем зафиксируйте верхний зажим.

Шаг 7

Откройте зеркальный источник света на стороне теодолита и посмотрите в маленький окуляр. Вы увидите три шкалы: горизонтальную, вертикальную и точную настройку. Используйте ручку точной регулировки в верхней части теодолита, чтобы выровнять метку с 0’00 «(0 минут и 0 секунд дуги).

Шаг 8

Используйте верхнюю горизонтальную ручку регулировки, чтобы выровнять единственную линию, которую вы видите в области действия в нижней половине горизонтальной шкалы, точно между двойными линиями, которые находятся ниже числа 0.

Шаг 9

Создайте контрольную линию, выровняв теодолит по горизонтали с высоким ориентиром в поле зрения. Разблокируйте нижний зажим, чтобы сделать это вращение, совместите прицел с ориентиром и снова заблокируйте нижний зажим. Горизонтальное измерение все равно будет нулевым. Отныне ослабляйте только верхний зажим, чтобы выполнить горизонтальные регулировки.

Измерение

Шаг 1

Разблокируйте верхний горизонтальный зажим и вращайте теодолит до тех пор, пока стрелка в точках обзора не выровняется с точкой, которую вы хотите измерить, затем заблокируйте зажим. Используйте верхний горизонтальный регулятор (не зажим), чтобы выровнять объект между двумя вертикальными источниками света в прицеле.

Шаг 2

Посмотрите в маленький окуляр и с помощью ручки точной регулировки установите точную горизонтальную линию с вашим объектом. Степени от вашего эталона измеряются по горизонтальной шкале градусов, минуты и секунды — по шкале точной регулировки (например, 30 градусов 10’30 «).

Шаг 3

Разблокируйте вертикальный зажим и просматривайте прицел, перемещая теодолит вверх и вниз, чтобы найти точное пятно по вертикали на вашем объекте, которое вы хотите измерить. Зафиксируйте зажим и используйте ручку точной вертикальной регулировки, чтобы точно зафиксировать точку, которую вы выбрали. Затем посмотрите в маленький окуляр и считайте градусы, минуты и секунды с вертикальной шкалы и шкалы точной настройки, как вы делали для горизонтальной шкалы. Если ваш объект находится высоко, вам нужно сначала выполнить грубую горизонтальную настройку, затем выполнить вертикальное измерение, а затем перенастроить для окончательного горизонтального измерения. Эти две координаты дают точный угол между вашей точкой отсчета и точкой интереса, но вы также можете измерить угол между двумя точками, сравнив их два измерения или установив первую точку в качестве точки отсчета.

Как построить прямой угол на земле при помощи простейших инструментов?

Как выставить угол 90 градусов без специального инструмента (угольника)? Допустим, у нас есть линия к которой нам нужно выставить перпендикуляр, т.е. еще одну

Теорема Пифагора

a²+b²=c²

Стороны a и b – катеты, между которыми угол равен ровно 90 градусов. Следовательно, сторона c – гипотенуза. Подставляя в эту формулу две известные величины, мы можем вычислить третью, неизвестную. А следовательно можем размечать прямые углы, а также проверять их.

Теорема Пифагора известна еще под названием “египетский треугольник”. Это треугольник со сторонами 3, 4 и 5, причем совершенно не важно, в каких единицах длинны. Между сторонами 3 и 4 – ровно девяносто градусов. Проверим данное утверждение вышеприведенной формулой: a²+b²=c² = (3×3)+(4×4) = 9+16 = (5×5) = 25 – все сходится!

А теперь применим теорему на практике.

Действительно ли прямой угол?

Как проверить прямой угол

Если вы хотите проверить, является ли ваше изделие или какая-то его часть строго прямоугольными, используя математику, сделайте следующее. Выберите один угол и с помощью комбинированного угольника предварительно проверьте, действительно ли он является прямым. Затем с помощью рулетки измерьте длину одной из сторон, составляющей прямой угол, и на калькуляторе умножьте полученное число на само себя (или, иными словами, возведите его в квадрат). Запишите это число или сохраните в памяти калькулятора.

Затем измерьте длину второй стороны, которая составляет прямой угол. Проделайте ту же операцию – умножьте это число на само себя. Затем сложите полученное число с тем, которые вы записали до этого. Одна часть уравнения готова!

Чтобы получить третью величину, измерьте расстояние от свободного конца одной стороны до свободного конца другой стороны. Это будет гипотенузой. Умножьте длину гипотенузы на саму себя. Если полученное число совпадает с суммой, которую вы получили до этого (когда складывали квадраты двух сторон), то угол действительно прямой.

Где нужен угол 90 градусов между стенами

Углы под 90 градусов в основном везде по квартире не выводятся. В эконом-ремонтах, да и в большинстве евро-ремонтах, выведенные в 90 градусов углы необходимы лишь в двух местах:

в том углу, где будет висеть/стоять кухонная мебель,
и в ванной комнате, где будет стоять сама ванна, в двух смежных углах (или в одном, если душевая кабина стоит в углу). Или по всем 4-м углам ванной, поскольку там будут стоять раковина, стиральная машина и т.п.

В остальных случаях — всё на желание заказчика или человека, осуществляющего ремонт своими силами.

Развернутый

Развернутый угол имеет такой вид:

В многоугольниках он не встречается, но не менее важен, чем все остальные. Развернутый угол — это геометрическая фигура, градусная мера которой всегда равняется 180º. На нем можно построить смежные углы, проведя из его вершины один или несколько лучей в любых направлениях.

Есть еще несколько второстепенных видов углов. Их не изучают в школах, но знать хотя бы об их существовании необходимо. Второстепенных видов углов всего пять:

Где нужен угол 90 градусов между стенами

Напольная плитка или потолочная, предметы мебели, ванная в классическом исполнении имеют строгую прямоугольную геометрическую форму. Установка подобных предметов, как правило, осуществляется вплотную к стенам. В случае с сантехническим помещением приходится предпринимать дополнительные действия для заполнения расхождений между краем оборудования и вертикальной поверхностью, когда угол имеет расхождения с 90 градусами.

Криволинейные щели вдоль тумбы или столешницы вынуждают проявлять аккуратность в пользовании, выглядят не эстетично и привлекают к себе излишнее внимание. Тоже касается плиточной раскладки. При этом скрыть значительное зауживание кладки невозможно будет даже визуально.

Выход из ситуации предполагает только три решения. Это визуальная маскировка заполняющими пустоту материалами, изготовление мебели по индивидуальным размерам с её суммарным удорожанием или выравнивание углов стен под обои, плитку, панели, предметы. Наиболее результативным считается последний вариант, так как он долговечен, значительно упрощает выбор относительно отделки и обстановки, так не придётся более ничего подгонять или заделывать.

Оригинальная маскировка неровного угла Источник blogspot.com

Как выровнять угол стены

Ровная поверхность — признак качественной работы штукатуров и шпаклёвщиков.

На неё можно клеить различные обои, покрывать краской, облицевать панелями или керамикой. Если же рабочих нет, как выровнять угол стены, сделать поверхность ровной, гладкой?

Для подведения углов под 90 градусов необходимы материалы, инструменты и определенные навыки.

Выбор угольников

Поверочные угольники представлены в специализированных торговых сетях в нескольких вариантах. Пожалуй, самый распространенный – это стальной слесарный угольник с широким основанием, изготавливаемый из инструментальной стали. Из габбро-диабаза изготавливаются угольники с широким основанием гранитные. Они имеют более высокую твердость, нежели стальные и не подвержены коррозии. Существуют угольники поверочные брусковые из твердокаменных пород. Все эти приборы производятся в соответствии с ГОСТом. Стандарты угольников брусковых предусматривают кроме допуска перпендикулярности допуски плоскостей измерительных и опорных поверхностей. Угольники с гибкой металлической линейкой представлены в самом большом ассортименте и используются чаще остальных форм. Собственно, множество модификаций инструмента имеют одну суть и одно предназначение.

Если проводимые работы требуют обязательного применения поверочного угольника, значит с его приобретением не стоит задерживаться. Поскольку угольники представлены в различных размерах, то следует учитывать масштабность предстоящих работ. Если нужно измерить какие-то детали в собираемом инструменте или проверить качество внутренней отделки при ремонте, то подойдет мелкий или средних размеров инструмент. Если же контролироваться будут крупные внешние конструкции, то и угольник должен быть соответствующий, массивный. Особенно это касается больших строительных площадей.

Для работ с мелкими конструкциями существуют малые модели поверочных угольников. Шкала на них имеет миллиметровую разметку, а вес колеблется от 70 до 100 г. Такие «малыши» очень востребованы при слесарных работах.

Выбирать угольник в специализированном магазине рекомендуется с помощью обычного бумажного листа стандартом А4. Этот листок, сложенный ровно пополам будет безупречным контролером идеальность прямого угла.

Кроме точности угла нужно проверить и качество поверочного угольника. Случается, что на дешевом экземпляре сантиметровые и миллиметровые деления нанесены так, что сотрутся при первом же применении. Поэтому, нужно убедиться, что разметка хорошо держится. Шкала обычно наносится на рабочую часть угольника. Но мастера, часто пользующиеся инструментом, считают, что удобство придает и наличие шкалы на самой ручке.

Очень важен материал, из которого изготовлена ручка инструмента. Деревянная модель надежно держится в руке. А вот металлическая и пластиковая требуют резиновых вставок во избежание скольжения пальцев. Обязательно надо подержать покупаемый инструмент в руках, чтобы понять, удобно ли будет с ним работать. Неудобный в использовании инструмент может привести к погрешностям в измерениях.

Приобретаемый инструмент должен быть крепким, с хорошо подогнанными элементами. Если линейка по отношению к ручке «ходит ходуном», такую модель надо оставить на полке магазина. Не стоит гнаться за дешевизной. Угольник должен быть надежным и послужить долго. Материал, из которого изготовлен инструмент, не должен быть восприимчив к каким-либо внешним воздействиям. Большие модели поверочных угольников предназначены для работ на улице, поэтому на них не должна действовать влага.

Существуют очень удобные модели поверочных угольников, снабженные контрольной ампулой с жидкостью. Она делает измерение идеально точным, не допуская малейших отклонений от плоскости. Такая модель предусматривает совмещение в одном инструменте строительного уровня и поверочного угольника. Это очень удобно, так как за один раз в руках находятся сразу два измерительных прибора.

Проверка прямого угла

Начнем с самого простого – проверки прямого угла с помощью теоремы Пифагора. Самым частым примером в отделке и строительстве является проверка перпендикулярности стен. Перпендикулярные стены – это стены, расположенные друг к другу под прямым углом 90°.

Итак, берем любой проверяемый внутренний угол. На стенах (на одной высоте) или на полу отмечаем на обоих стенах отрезки произвольных длин. Длинна этих отрезков произвольная, по возможности нужно отмечать как можно больше, но чтобы между отметками на стенах удобно было мерить диагональ. Например, мы отметили 2,5 метра (или 250 см.) на одной стене и 3 метра (или 300 см.) на другой. Теперь длину отрезка каждой стены возводим в квадрат (умножаем саму на себя) и получившиеся произведения складываем. Выглядит это так: (2,5×2,5)+(3×3)=15,25 – это диагональ в квадрате. Теперь нужно извлечь из этого числа квадратный корень √15,25≈3,90 – 3,9 метра должна составлять диагональ между нашими отметками. Если измерение рулеткой показывает другую длину диагонали – проверяемый угол развернут и имеет отклонение от 90°.

Калькулятор расчета диагонали прямого угла

Длина

Длина b

Диагональ c

Извлечение квадратного корня никогда меня не привлекало – простому человеку не обойтись без калькулятора, к тому же, не на всех мобильных устройствах калькуляторы умеют извлекать его. Поэтому можно пользоваться упрощенным методом. Нужно лишь запомнить: у прямого угла со сторонами ровно 100 сантиметров, диагональ равна 141,4 см. Таким образом, у прямого угла со сторонами 2 м. – диагональ равна 282,8 см. То есть на каждый метр плоскости приходится 141,4 см. У этого метода один недостаток: от измеряемого угла нужно откладывать одинаковые расстояния на обеих стенах и отрезки эти должны быть кратны метру. Не буду утверждать, но по моей скромной практике – это гораздо удобнее. Хотя не стоит забывать о первоначальном способе совсем – в некоторых случаях он очень актуален.

Выравнивание углов гипсокартоном

Можно начинать выравнивание. Выровнять угол с помощью гипсокартона можно двумя способами: с монтажом каркаса без него.

Каркасный метод стоит использовать, если стена кривая и перекос достаточно большой и составляет свыше 20 мм. Этот способ более эффективен, однако, сложнее и обойдется дороже. Преимуществом каркасного метода является возможность дополнительной тепло и звукоизоляции, которую можно поместить в пространство между основанием и гипсокартоном.

Выравнивание внутренних и внешних углов каркасным методом отличаются друг от друга. Рассмотрим сначала выравнивание внутреннего угла.

Из своего опыта скажу, что лучше сначала смонтировать каркас отдельно и затем прикрепить его к поверхностям стен, потолка и пола, поскольку монтировать каркас сразу в угол очень неудобно. Сооружать каркас необходимо на ровной поверхности. Если пол у вас кривой, то можно использовать лист гипсокартона для этой цели, только делайте все аккуратно, чтобы не испортить лист.

Итак, приступим. Соберите из профиля одну сторону угла, а затем прикрепите перпендикулярно другую. Соединение кусков профиля делается при помощи саморезов. Сверху и снизу каркас скрепите поперечинами из того же профиля. Важно, чтобы саморезы острыми концами смотрели в стену или вдоль профиля, а наружная часть была гладкой.

У вас должен получиться достаточно жесткий каркас, на который и будет крепиться гипсокартон. Прикрутите ваш каркас к профилю, который должен быть заранее установлен по периметру (вдоль пола и потолка). В случае, если потолки очень высокие, то прикрепите каркас к стене (примерно посредине).

Далее необходимо обшить каркас листами гипсокартона. Делается это такими же саморезами, какими мы и соединяли профиль для каркаса.

Теперь я опишу, как выровнять внешний угол гипсокартоном.

Внешний угол выровнять гораздо проще, поскольку можно монтировать каркас сразу, а не сооружать его отдельно. Первым делом прикрепите с каждой стороны угла профиль по высоте стены и скрепите оба эти профиля с теми, которые уже проложены по периметру (вдоль пола и потолка). Затем прикрепите листы гипсокартона. В место соприкосновения двух листов в угле – снимите фаски примерно на пол толщины листа. Это визуально сделает стык в итоге более ровным. Фаску можно снять нождачкой.

Теперь рассмотрим вариант выравнивания углов без каркаса. Этот способ подойдет, если перекос стены не слишком кривая, а перекос небольшой и составляет 4-8 мм. Первым делом необходимо очистить и прогрунтовать основание. Выбирайте грунтовку глубокого проникновения. После того как стены высохнут, нужно сделать мерки путем прикладывания листа к стене. Отмечаем местоположение листа карандашом, чтобы соединение получилось стык в стык.

Затем наносим слой монтажной пены на гипсокартон и прижимаем его к основанию. Часть пены останется на стене, что обеспечит лучшее сцепление. Потом наносим еще один слой пены, ждем 3-5 минут, и клеим лист. После этого прямой рейкой при помощи уровня выводим прямой угол.

Делаем разметку под выравнивание прямых углов

Поскольку работа по выведению всех углов в 90 градусов своими руками достаточно трудоёмкая и ресурсозатратная (штукатуркозатратная©), сначала посмотрим геометрию помещения и потом примем решение о том, какие углы будем делать прямыми, а какие оставим как есть (два угла или все), если это решение ещё не принято. В любом случае 4 угла будет сложнее и дороже чем 2.

Возьмём для примера ванную комнату и предварительно проверим углы угольником по всей площади и посмотрим примерно какая картинка у нас вырисовывается.

Угольником проверяем углы

Картинка у нас совсем не радостная, один угол (левый нижний) совсем ушёл. С остальными углами всё более-менее, но ванная напротив двери не встанет, точнее встанет, но образуются зазоры между ванной и стеной. Небольшие зазоры можно перекрыть плинтусом для ванн (3-5 мм, даже до 1 см), а вот больше уже ничем не перекроешь. Точнее, и больше можно, хоть 3-5 см, но качество… качество будет совсем не то.

Давайте теперь сделаем тоже самое, только удлиним наш угольник прави́лом и от угла к углу в итоге начертим внутри нашего помещения прямоугольник.

Как можно вычислить прямой угол?

Итак, нужно обозначить следующие шаги:

Для начала стоит разобраться в том, почему принцип так обозначен — 3-4-5. Это не просто набор цифр, это величина сторон прямоугольного треугольника. Теорема Пифагора гласит: квадрат гипотенузы равен сумме квадратов катетов. Цифры 3-4-5 очень подходят для проверки этого простого правила геометрии: 3*3+4*4=5*5, то есть 9+16=25. Именно эти цифры и будут использоваться в дальнейших вычислениях;
Итак, потребуется для начала отмерить 3 метра от угла вдоль одной из стен. Тут следует отметить, что 3 метра — предпочтительная длина замера, но в том случае, если комната маленькая, можно отметить всего 30 сантиметров. В месте замера нужно сделать отметку;
В принципе, можно использовать и другие цифры, но рекомендуется в любом случае использовать пропорционально увеличенные числа, например: 9-12-15 или же 30-40-50;
После проделанного предварительного замера нужно отмерить 4 метра вдоль другой стены, тоже от угла. Ну или соответственно 40 сантиметров, если комната маленькая. Нужно сделать отметку;
Теперь остаётся сделать последнее действие, по которому уже можно судить прямой угол или нет. От измеряющего потребуется измерить расстояние между сделанными отметками. По полученным данным можно будет сделать определённые выводы:
- Если расстояние между отметками будет равняться 5 метрам ровно, это будет означать, что угол является прямым;
В том случае, если измеренное расстояние будет равняться меньше 5 метров, угол будет меньше, чем 90 градусов;
Ну и, наконец, величина угла будет составлять больше 90 градусов, если полученная величина замера будет равняться больше 5 метров.

Об этой статье

Эту страницу просматривали 65 588 раз.

Видео описание

Из видео можно узнать об инновационном комбинированном способе установки маяков с помощью креммеров:

Что мы знаем об инструменте?

Если разобраться, то героиня нашего исследования, линейка – простейший измерительный инструмент. Это такая пластина, у которой одна из сторон однозначно прямая, на неё наносят деления, которые будут кратны единицам измерения длины. У нас это будут сантиметры, в некоторых европейских странах – дюймы.

Ещё со школы мы знаем, что линейки делают деревянными, пластиковыми и металлическими. Сначала мы учимся с их помощью проводить поля в тетрадках. Позднее, на уроках геометрии уже чертим линии, потом фигуры, замеряем расстояние при помощи измерительного циркуля, а потом смотрим, сколько это, приставив его все к той же линейке. На помощь обычной линейке уже приходят её собратья – угольники. Помните, это такие линейки с углами 30 и 60 или двумя по 45 градусов. А еще же транспортиры, да и не только они.

Есть огромное множество специальных линеек, которыми пользуются ученые, инженеры, штурманы, врачи, закройщики, строители и целый ряд других специалистов. Однако родоначальницей их была наша героиня, которая и сегодня для многих из нас оказывается незаменимой и верной помощницей в быту, при домашнем ремонте или дачном строительстве.

Правила пользования

В школе объясняют, что такое транспортир, на уроках математики. Именно здесь есть необходимость в измерениях.

Для того чтобы нам узнать, чему равен один градус, нужно окружность поделить на 360 равных частей. Одна из таких частей и будет равна 1 градусу. Величина окружности никак не повлияет на градус! Это легко проверить.

Нарисуем две окружности разного диаметра и поделим каждую на 360 равных частей. Затем наложим меньшую окружность на большую и увидим, что линии совпали.

Как угломером ун измерить угол меньше 90

Угломер – это точный прибор, предназначенный для измерения углов между двумя поверхностями или их наклона относительно горизонта. Получаемые результаты выражаются в градусах. Угломеры имеют схожую конструкцию со строительным или столярным уголком, но они могут показывать не только угол в 90 градусов, но и регулироваться.

Простейшая конструкция угломера

Конструкция угломера в самом простом виде состоит из двух пластин (линеек). Они закрепляются вместе с одной стороны, фиксируясь с помощью оси, позволяющей менять угол между ними. На поверхности инструмента имеется шкала, выраженная в градусах. Она может быть линейчатой или скругленной. Существуют как полностью подвижные угломеры, так и с фиксированными измерениями. Последние используются в тех случаях, когда требуется только измерение самых важных углов – 90, 45 и 30 градусов. Такой инструмент больше относится к категории шаблонов.

В каких отраслях используется угломер

Этот прибор широко используется в строительстве. Его применяют столяры, плотники и монтажники. С его помощью можно выставить плоскости идеально ровно перед их закреплением. Подавляющее большинство предметов, которые используются в быту, и на промышленных объектах, имеют углы по 90 градусов. Это установленный международный стандарт, который обеспечивает максимальное удобство. Кроме этого, несоблюдение угла 90 градусов в строительстве вертикальных элементов увеличивает нагрузку на конструкцию.

Например: Благодаря тому, что углы зданий вымеряются точно, то при установке угловой ванны, под стеной не образуется зазор и при развешивании шкафчиков и полок все выглядит ровно. Существует еще тысячи примеров, которые позволяют визуализировать пользу точного соблюдения углов. Применение угломеров позволяет обеспечить точную передачу параметров отображенных на чертеже на реальный объект.

Также угломеры используется при построении маршрутов, в военном деле, геометрии и астрономии. В связи с востребованностью этого инструмента, его конструкция была адаптирована под различные цели измерения.

Угломеры можно разделить на виды:

Строительный.
Слесарный.
Плотницкий.
Горный.
Астрономический.
Мореходный.
Артиллерийский.

Строительный угломер является самым распространенным. Он применяется для контроля уровня стен, фундамента и других конструкций. Такие устройства являются довольно габаритными. Длина каждой измерительной части обычно составляет не менее 50 см.

Слесарные имеют высокую точность. Они довольно компактные, при этом имеют довольно чувствительную регулировку, позволяющую проводить измерения с отображением долей градуса. Это необходимо, поскольку малейшие отклонения от нормы недопустимы. С такими угломерами можно спокойно вымерять параметры деталей, которые будут использоваться во вращательных механизмах.

Плотницкие угломеры отличаются низкой точностью измерения. Они используются в деревообработке, когда точное соблюдение углов и долей градусов не имеет никакого значения. Такой инструмент относится к низкой ценовой категории. Зачастую механизмы регулировки имеют люфт, что также приводит к погрешности. Несмотря на это, подобная разновидность угломеров вполне приемлема для выполнения тех целей, для которых она предназначена.

Горные угломеры в отличие от предыдущих разновидностей данных инструментов не используется для непосредственного контакта с измеряемыми поверхностями. Данный инструмент позволяет визуально определить вертикальные и горизонтальные углы в пространствах шахт и горных выработок. Данное оборудование относится к неточному классу. Сейчас оно практически не используется в связи с появлением более высокоточного электронного оборудования, такого как тахеометры и пр.

Астрономические являются самыми точными. Они применяются для измерения угла между поверхностью земли и точками на небосводе. С их помощью высчитывается траектория движения небесных тел, определяется скорость их перемещения, а также оценивается величина объекта. Такие устройства зачастую интегрированы в телескопы, что расширяет диапазон их измерений, поскольку объектом исследования могут стать не только видимые на небосводе объекты, но и отдаленные звезды и планеты.

Мореходные угломеры также называют навигационными. С их помощью осуществляется определение географической широты с использованием специальной таблицы. Данные устройства работают по принципу, что небесное светило (солнце, луна или звезды) в определенный день и время находится над горизонтом под особенным углом, относительно географической широты. Таким образом, используя данный прибор и таблицу, наблюдатель может определить широту, на которой он находится в данный момент. Это устройство широко использовалось мореходами в прошлом, но с развитием спутниковых технологий, его применение отошло на второй план. Несмотря на это, подобные угломеры имеются на борту многих судов, поскольку в случае отказа электронного оборудования, использование ручного прибора будет единственной возможностью получить точные координаты судна.

Артиллерийский угломер используется для установки артиллерийского орудия и корректировки залпового огня. Применение такого инструмента позволяет осуществлять точное прицеливание и вносить изменения направления выстрела после предварительного пристреливания

Виды угломеров по принципу измерений

По принципу измерений угломеры разделяют на следующие виды:

Механические.
Маятниковые.
Оптические.
Лазерные.
Электронные.

Механический угломер относится к контактным устройствам. Чтобы осуществлять измерение необходимо приложить обе поверхности инструмента к тем объектам, угол между которыми нужно измерить. На устройстве имеется специальная шкала, позволяющая определить, какой угол между сторонами инструмента получен. Поскольку стороны плотно прилегают к измеряемым поверхностям, то соответственно их угол будет также равен шкале.

Маятниковый угломер внешне напоминает стрелочные часы. На круглый циферблат инструмента нанесена разметка соответствующая углам. Стрелка такого угломера всегда стоит идеально вертикально вне зависимости от того насколько выгнут непосредственно сам прибор. Внизу корпуса устройства имеется небольшая линейка. Она прикладывается к поверхности, которую необходимо измерить, после чего нужно посмотреть на показатель образованного угла между отметкой «0» на циферблате и стрелкой. С помощью такого прибора можно измерить уровень наклона одной поверхностей.

Оптический угломер имеет непривычную для этого оборудование форму. Узнать оптические угломеры можно по глазку, выполняющему функцию лупы. Оптические инструменты имеют диапазон измерения 360 градусов. Они являются очень точными, поскольку на шкале нанесено множество отметок не только в градусах, но и в их долях. В связи с этим сложно визуально определить, на какой показатель указывает стрелка. У оптических имеется увеличительная лупа. Благодаря ей гораздо легче посчитать отметки, на которые указывает стрелка на шкале.

Лазерный угломер имеет в своей конструкции два лазерных луча, направляющихся на поверхности, между которыми необходимо измерить угол. Угол между точками измеряется визуально либо с помощью вычислительного электронного элемента, который интегрирован в конструкцию устройства. Такое устройство хорошо работает в ночное время, а также в помещениях. На дневном свете лазерный луч практически незаметен.

Электронные или цифровые угломеры по принципу действия похожи на механические. За тем исключением, что у них имеется циферблат в виде ЖК-дисплея, на который выводится показатель в цифрах. Это очень точное оборудование, позволяющее определять десятые части градусов. Для питания подобного устройства используется обычная пальчиковая батарейка. Такие инструменты используют строители и монтажники.

Как работать контактными угломерами

Угломеры контактного типа являются самыми распространенными и недорогими. Их используют повсеместно. Для проведения измерения необходимо приложить инструмент к углу, который необходимо измерять. Одна линейка угломера прижимается к одной поверхности, а вторая к другой. При необходимости устройство необходимо подкорректировать, увеличив или уменьшив угол между его сторон. Результаты измерения отображаться на механической или электронной шкале. Чтобы данные получились максимально точными, необходимо чтобы поверхности в точках контакта были ровными. Если, к примеру, измеряется угол между полом и стеной, необходимо, чтобы на них не было наслоений в виде прилипших комков строительного раствора или клея. Такая крупинка под одной из линеек нарушит получаемые данные на несколько градусов.

Как выбрать угломер

При выборе следует обратить внимание на материал. Если он изготовлен из очень тонкого металла, то брать подобный инструмент не стоит. Со временем он деформируется, поэтому точность измерений будет нарушена. У более дешевого ассортимента зачастую шкала нанесена краской. В результате со временем краска начинает отслаиваться. После этого определить, на сколько градусов показывает инструмент невозможно.

Стоимость угломера зависит не только от его конструкционных особенностей, но и точности. Чем выше точность, тем меньше люфты на оси настройки, что требует более затратного производства. Для столярного дела или малоэтажного строительства вполне можно обходиться инструментами более низкой категории, но для изготовления ответственных деталей, нужно точное оборудование.

Министерство образования и науки Российской Федерации

Тульский государственный университет

Кафедра «Инструментальные и метрологические системы»

МЕТРОЛОГИЯ, СТАНДАРТИЗАЦИЯ И СЕРТИФИКАЦИЯ

Лабораторная работа № 12

Измерение углов с помощью универсального угломера

Целью работы является ознакомление студентов с методами измерения углов деталей машиностроения.

Методы измерений углов могут быть разбиты на три основные группы:

1. Методы измерения сравнением с жесткими одномерными образцовыми угловыми мерами (угловые меры, шаблоны, угольники).

2. Гониометрические методы измерений. Определение величины угла непосредственно в угловой мере.

3. Тригонометрические методы. Измерение линейных величин необходимых для определения угла.

Рассмотрим первые два метода измерений.

1. Угловые меры применяются при лекальных работах и для проверки измерительного инструмента и приборов.

Угловые меры представляют собой стальные плитки, доведенные измерительные поверхности которых образуют один или несколько определенных рабочих углов (рис.1).

На рис.1a изображена плитка с одним рабочим углом, на рис.1б-плитка с четырьмя рабочими углами.

С помощью плиток можно измерить углы в пределах от 100 до 360°, набор из 93 штук позволяет составить блоки через 30′, набор из 36 штук-через 1’.

Блоки крепятся при помощи специальных державок (рис. 1в и 1г). Набираются они по тем же правилам, что и при составлении блоков из концевых мер длины.

Рис.1. Угловые меры

При проверке контролируемый объект должен точно, без просветов, прилегать обеими образующими угла к измерительным плоскостям блока плиток.

На рис. 1в и 1г измеряемый объект показан штриховкой.

2. При измерении гониометрическим методом сравнивают измеряемый угол со шкалой прибора. В данной работе будет использоваться только угломер с нониусом (рис.2).

Угломер с нониусом состоит из транспортира с делениями от 0° до 120° через один градус, подвижной линейки 2, вращающейся вместе с нониусом на оси 3, съемного угольника 1 и микрометрического винта 4.

Цена на нониусе может быть 2’, 5’ или 15’. При точной установке на определенный угол гайка 5 закрепляется и с помощью микрометрического винта 4 линейка 2 вместе с нониусом приводится в требуемое положение. Стопор 6 служит для закрепления линейки 2 в необходимом положении.

Для измерения углов от 0° до 90° на подвижную линейку 2 надевается съемный угольник I. Измерение углов от 90° до 180° проводится без съемного угольника.

Рис.2. Угломер с нониусом

При измерении какого-либо угла угломер устанавливается на сторонах угла таким образом, чтобы между линейками прибора и измеряемой деталью не было просвета. Отсчет на угломере равен сумме отсчетов на основной шкале и нониусе. Первый отсчет равен целому числу градусов, соответствующему делению основной шкалы, расположенному перед нулевым делением нониуса. Отсчет на нониусе равен числу делений на нониусе от 0 до деления, совпадающего с каким-либо делением на основной шкале, умноженному на цену деления шкалы нониуса.

При отсчете следует помнить, что цифры на нониусе соответствуют не номерам рисок, а уже количеству минут.

3. Задание на работу

3.1. Ознакомиться с устройством угломера.

3.2. Измерить углы у детали по указанию преподавателя.

3.3. Усвоить измерение углов с помощью угловых плиток.

3.4. Оформить отчет и ответить на вопросы преподавателя.

4. Контрольные вопросы

1. Как перенастраивается прибор при контроле острых углов и при контроле тупых углов?

2. Установите прибор на показание, равное 13° 25’; 40° 30’; 112° 10’ (для угломера с ценой деления нониуса 5′).

3. Где используются угловые плитки?

Лаборатория линейных и

ИЗМЕРЕНИЕ УГЛОВ С ПОМОЩЬЮ УНИВЕРСАЛЬНОГО УГЛОМЕРА

ПРИМЕР ОФОРМЛЕНИЯ РАБОТЫ

Задание. Измерить угломером завода “КРИН”, имеющим нониус с точностью 5’ , деталь по указанию руководителя

В машиностроении в качестве единицы измерения используют градусы (1/360 окружности), минуты (1/60 градуса) и секунда (1/60 минуты) (1 рад. = 360/2 = 571744,8).

Для призматических деталей кроме углов допускается применение уклонов, например: уклон 1:500 соответствует углу уклона  = 652,5 или 0,002 радиана.

Для конусов, наряду с углами используется понятие конусность:

где D – d – разность диаметров двух поперечных сечений конуса; L – расстояние между этими сечениями.

Конусность часто выражают в виде отношения, например, С=1:20, где 20 – расстояние между поперечными сечениями конуса, разность диаметров которых равна 1 мм.

Нормальные углы, обычно применяемые в машиностроении, регламентируются ГОСТ 8908-81 (таблица П7.1). Приведенные в этом документе значения нормальных углов не распространяются на углы, связанные расчетными зависимостями с другими размерами и на углы конусов.

Нормальные конусности и углы конусов приведены в ГОСТ 8596-81. Стандартом предусмотрены два ряда конусности и углов конусов с предпочтительным применением первого ряда перед вторым. Наряду с этим для специального применения предусмотрена конусность для инструментальных конусов (конуса Морзе с номерами от 0 до 6).

Допуски углов конусов и призматических элементов деталей с длиной меньшей стороны до 2500 мм регламентирует ГОСТ 8908-81. Стандартом установлены 17 степеней точности углов, самая точная 1 степень, самая грубая 17. Допуск угла, выраженный разностью между наибольшим и наименьшим предельными углами, обозначается АТ, а допуск угла заданной точности дополняется номером соответствующей степени точности, например: АТ8 и т.д.

Величины допусков на углы определены в зависимости от наименьшей стороны угла, так как точность изготовления и измерения угловых размеров зависит от длины стороны и чем она меньше, тем точность ниже (таблица П7.2).

Лабораторная работа № 7. Измерение углов угломерами

1. Цель работы

Изучение устройства универсальных угломеров и приобретения навыков по их применению.

2. Краткая теоретическая часть

Для измерения углов в производственных условиях промышленность выпускает универсальные угломеры. В качестве отсчетного устройства у этих угломеров используется нониус, как у штангенциркуля, но проградуированный в угловых единицах.

В России выпускаются транспортирный и универсальный угломеры с нониусом.

Рис. 4.1. Универсальный угломер

Универсальный угломер (рис. 4.1) состоит из основания 4 с угловой шкалой, имеющей диапазон показаний 90 и цену деления 1. На основании закреплены основная линейка 10 и подвижный сектор 9 с нониусом 8. Стопор 7 фиксирует сектор в нужном положении. С помощью державки 6 к сектору можно прикрепить угольник 2, к которому державкой 3 можно прикрепить съемную линейку 1. Последнюю можно также установить прямо на сектор 9. В полностью собранном виде между плоскостями основной и съемной линейки измеряют углы от 0 до 50. Если на секторе 9 установлена съемная линейка 1, то измерения выполняются в пределах от 140 до 200. Между плоскостями сектора 9 и основной линейки 10 измеряются углы в пределах от 230 до 320. Полный диапазон измерений универсального угломера составляет 0-320, отсчет по нониусу составляет 2.

Рис. 4.2. Транспортный угломер

Транспортирный угломер (рис. 4.2) измеряет наружные углы в пределах от 0 до 180. Принцип работы угловых и линейных нониусов, а также отсчет по ним одинаковы. Допускаемые погрешности угломеров равны значению отсчета по нониусу. Основным недостатком этих угломеров является неудобство снятия показаний.

Выше указанного недостатка лишены оптические универсальные угломеры. Отсчет по нониусу у этих угломеров снимается через специальную лупу. Схема такого угломера показана на рис. 6.3.

Оптический угломер предназначен для измерения углов от 0 до 360. Он состоит из корпуса, с которым жестко связана сдвоенная линейка. Сменная линейка поворачивается и перемещается в продольном направлении. Съемная подставка с зажимным винтом используется при измерении углов цилиндрических или конических поверхностей. Отсчет осуществляется с помощью лупы. В лупу видна основная градусная шкала, а также прямая и обратная минутные шкалы с ценой деления 5. Допускаемая погрешность оптического угломера составляет 230, а при измерении с подставкой она составляет 5.

Изображенный на рис. 4.3 угломер фирмы Mahr состоит из корпуса 7, сменной линейки 1 и круговой шкалы 3. На круговой шкале нанесены деления через один градус. Шкала нониуса рассматривается через линзу 4. Линейка крепится на корпусе угломера с помощью винта 2. Для точной подачи линейки относительно корпуса используется винт точной установки 6. Фиксация угломера в нужном положении осуществляется стопорным винтом 5.

Рис. 6.3. Универсальный оптический угломер 106 UF

Отсчет целых градусов осуществляется по делению основной шкалы, которое ближе всего расположено к нулевому делению нониуса. Значения минут снимают по делению нониуса, которое совпадает, с каким либо делением основной шкалы.

Как сделать угольник 90 градусов своими руками. Как разметить фундамент

Откосы под 90 градусов

[ Нажмите на фото
для увеличения ]

Вероятнее всего — углы далеки от идеала. Как же выставить маяки так, чтобы все углы помещения были 90 градусов? А всё проще простого.

Вам из дополнительных инструментов потребуется лишь угольник. Рассмотрим весь технологический процесс более подробно. Разметьте одну стену под маяки. Просверлите отверстия под саморезы. Вставьте саморезы по дереву в распорные пластмассовые дюбеля, которые вы предварительно вставили в просверленные отверстия.

Выставите их по уровню. Оштукатурьте эту стену. Для чего? У вас тогда будет готова одна плоскость, от которой вы будете выставлять 90 градусов для примыкающих к ней двух стен. На одной из стен, которые примыкают к оштукатуренной плоскости, рядом с углом, отметьте вертикальную линию.

Просверлите отверстия в ней для дюбелей. Вставьте в эти отверстия дюбеля. Вкрутите саморезы. Теперь надо выставить саморезы линии по уровню. Берите угольник. Маленькой стороной прикладывайте к готовой поверхности стены, а длинной стороной на один из выставленных саморезов.

Отметьте линию, чтобы она не выходила за пределы стороны угольника. Потом рисуйте вертикальную линию по отмеченной линии. Просверлите отверстия на линии параллельно саморезам на первой вертикальной линии, которые уже выставлены по уровню. Вкрутите саморезы. Далее.

Приложите угольник к оштукатуренной поверхности и на саморез первой линии. Смотрите, что получилось. Если саморез второй линии не касается угольника, подкрутите его отвёрткой до того момента, чтобы саморез коснулся угольника. Так выставляйте все саморезы второй линии. Теперь у вас получилась ровная линия по уровню и с углом 90 градусов.

Размечайте далее всю стену линиями для маяков и выставляйте на них саморезы. Только саморезы должны находиться на одной горизонтальной линии с саморезами первой и второй линии. Берите правило и приложите его к двум саморезам первой и второй линии горизонтально. Смотрите на саморез третьей линии. Подкрутите его отвёрткой до правила. Так выставляйте все саморезы.

Допускаются некоторые отклонения от нормы, но не более 1мм.

Потом переходите дальше. Как выставите маяки на этой стене — оштукатуривайте её. И снова выставляйте маяки. Когда вы оштукатурите все стены, шпателем широким зачистите углы от лишнего раствора. Углы должны быть ровными и чистыми. Ваши углы будут ровно 90 градусов — это гарантировано.

На внешние углы обязательно ставьте перфорированный уголок. По уровню, разумеется. Справа и слева от уголка нанесите жидкий слой штукатурки. Протяните его большим правилом. Роль маяка сыграет уголок, а роль второго маяка — конец самого правила. Это сделает ваши стены идеально ровными.

Допускаются некоторые отклонения от нормы, но не более 1мм. Старайтесь, чтобы было меньше ям и царапин. Тогда шпаклевать будет намного легче и расход шпаклёвки будет минимальный. В ванной комнате и туалете маяки извлекать не стоит. Да и жидким слоем проходить не надо. Там ведь всё равно будет плитка.

Если у вас в санузле будут углы 90 градусов, то плитка будет смотреться просто изумительно. Потому что идеальные углы — это красиво. Обои или краска на стенах помещения с идеально ровными углами также будут выглядеть идеально, без погрешностей.

Технологии

Техника сграффито – шаг к совершенству вашего интерьера
В последнее время очень часто в качестве отделки стала применяться цветная декоративная штукатурка, которая прекрасно подходит для отделки фасадов зданий и различных элементов архитектуры

Шелковая штукатурка – изюминка в дизайне помещений
Многие дизайнеры в последнее время часто используют шелковые штукатурки для отделки стен. Что они собой представляют? Разберемся в чем их красота и изюминка?

Штукатурка: виды, назначение, техника работы
Штукатурка – материал, предназначенный для ведения строительных работ. Технология нанесения штукатурки подобна технологии для шпатлевок за небольшим отличием – штукатурка не шлифуется абразивными материалами

Штукатурка поверхностей машинным способом – преимущества
Штукатурка стен — один из важных этапов отделки помещения. При незначительных объемах работ штукатурку наносят вручную, а на объектах более 300 м2 требуется машинное нанесение штукатурки

Подготовка поверхности к оштукатуриванию
Штукатурка считается основной работой выравнивания поверхности, а также является подготовкой для очередного этапа ремонта. Сама технология оштукатуривания тоже нуждается в подготовительном этапе

Математика. Это страшное для многих слово , которое пугало достаточное количество школьников в своё время. Цифры, формулы и расчёты поддавались только самым пытливым. И с каждым годом этот сложный предмет становился всё сложнее и сложнее.

В данной статье речь пойдёт о вычислении прямого угла, что требуется при строительстве зданий. Точность при возведении строений должна быть соблюдена в обязательном порядке , ведь только точные расчёты могут избавить от перекосов и нестабильности организации всего здания. Вычисление прямого угла при строительстве — не такой уж и трудный процесс, при котором потребуется знание и применение некоторых простых правил математики и геометрии. Подробнее об этом будет рассказано ниже.

Действительно ли прямой угол?

И, в принципе, они правы. Получить его весьма сложно, особенно если наблюдается неровность фундамента, на котором осуществляется строительство здания. Но, даже учитывая это обстоятельство, ни в коем случае нельзя делать вывод , что расчёт прямого угла можно делать просто «на глаз». В любом случае, если не представляется возможным вычислить идеальный прямой угол, то требуется достичь наиболее приближённого значения к идеальному углу в 90 градусов. И этого можно добиться, используя незатейливые инструменты и не самые сложные математические знания и познания в геометрии.

Что понадобится для определения прямого угла?

Для вычисления прямого угла нужно взять:

Карандаш;
Строительную рулетку.

И всё. Вот так вот всё просто.

Как можно вычислить прямой угол?

Итак, нужно обозначить следующие шаги:

Вывод

Вот, как просто можно вычислить прямой угол без использования каких-либо строительных инструментов и приборов. Использовать можно самое простое, но в то же время весьма действенное средство , которое вкупе с использованием имеющихся знаний и бесхитростных расчётов, может помочь произвести измерение.

Способы выравнивания внутреннего и внешнего углов. Применение материала и инструмента. Вычисление ровного угла, способы определения угла на 90 градусов.

Как выровнять угол стены

Ровная поверхность — признак качественной работы штукатуров и шпаклёвщиков.

Для подведения углов под 90 градусов необходимы материалы, инструменты и определенные навыки.

Зачем необходимо выравнивание угла стены

Ровные стыки стен в помещении – опрятный внешний вид. Если кривые стены можно скрыть за обоями и картинами, то углы сделают комнату неопрятной.

Еще одним недостатком кривизны мастера считают сложность монтажа плитки, поклейка обоев, другое финишное покрытие. Для выравнивания стыков стен нужно потрудиться, однако, в последующем это отразится на внешнем виде и опрятности.

Как выровнять внутренние углы стен в комнате своими руками

Для выравнивания внутренних стыков надо провести подготовительные работы.

Очищенную поверхность от плитки или обоев проверяют на наличие пустот под штукатуркой. Надо простучать смежные стены от потолка до низа. В случае изменения звука (пустой) штукатурку лучше обвалить. Иначе она может сама отпасть вместе с финишным покрытием. Еще одним признаком пустоты являются мелкие трещины, идущие горизонтально полу.
После обваленного покрытия, убирают весь мусор. Это пыльная работа, но это не будет мешать в последующей работе.
Всё зачищают от пыли и мелких камушков сухой щеткой. Для уменьшения пыли можно место сбрызнуть водой с опрыскивателя.
Далее, поверхность покрывают грунтовкой, желательно 2 раза.
От потолка к полу опускают отвес для выяснения кривизны. При выявлении больших отклонений лучшим вариантом является гипсокартон. Иначе штукатурный слой придется накладывать несколько раз, каждый высохший слой при этом грунтуют.

Внутренний угол можно выровнять несколькими методами. Кроме гипсокартона, применима обычная гипсовая или цементная штукатурка, маяки, угловые шпатели.

Чем в квартире выравнивать ранее оштукатуренные стены

Если стена кривая, то выравнивание стыка будет напрасной работой. Кривые оштукатуренные стены надо выявить на процент кривизны. Это можно сделать уровнем, отвесом, правилом. Стены выравнивают по кругу.

Для выравнивания стен применимы материалы:

Гипсокартон. При больших перепадах применяют каркасную металлическую основу. Если стены имеют небольшую кривизну, тогда ГКЛ клеят на поверхность.
ДСП. Применимы плиты для выравнивания не очень кривых поверхностей.
Панели. Выравнивая стены, применяют каркасную основу.

В зависимости от помещения, влажности и перепадов температуры выбирают нужный материал.

Как вывести угол 90 градусов на стенах

При самостоятельном оштукатуривании стен и выравнивании стыков применяют штукатурный угловой профиль. Он может быть металлическим и пластиковым. По сторонам от уголка идет армированная сетка. Профиль накладывают на сырую штукатурку и с помощью уровня выставляют его. Армированная сетка покрывается штукатурной смесью.

А также стыковочную поверхность можно сделать ровной с помощью углового шпателя. Он имеет идеально ровную форму. Не прилагая усилий, с его помощью создают стык стен на 90 градусов.

Самостоятельно вывести 90 градусов сложно. Это возможно только при небольших перепадах, где применима шпатлёвка.

С помощью каких материалов производится выравнивание дерева

Деревянная поверхность также нуждается в предварительной обработке с последующим выравниванием. Выровнять деревянную поверхность можно с помощью материалов:

Гипсокартон. Для монтажа надо сначала измерить степень кривизны, после чего сделать замеры и расчет материалов. Каркасную основу создают из деревянных реек либо металлических профилей. Для прочного каркаса делают поперечные ребра жесткости. Крепление ГКЛ в углах производят по нескольким технологиям. Стыки стен получаются ровными под 90 градусов.
ДСП. Также крепят на каркасную основу, созданную из дерева. Все элементы обрабатывают олифой или же антисептическими средствами.
Фанера 6-9 мм. Её следует обработать. В основном применяют материал для выравнивания поверхностей в гараже, кладовой, дачном домике. Для крепления также создают каркас из дерева.

После, созданную поверхность с ровными углами шпаклюют, грунтуют покрывают финишным материалом – обои, краска, плитка.

А также стены и их стыки деревянного дома выравнивают материалами:

шпатлевка – слой накладываемой смеси 2 мм. Перед нанесением шпаклевки надо обработать стены;
цементные растворы – накладывают на шершавую поверхность либо же предварительно набивают дранку или крупную сетку;
применение уголков. Если стены ровные или имеют небольшие перепады на шпаклевочный раствор крепят металлические или пластиковые уголки. При этом после повторного слоя шпаклевки угол равен 90 градусов.

Цементный раствор дает усадку. При накладывании толстого слоя следует следить за тем, чтобы созданная плоскость не потекла вниз.

Как сделать ровными наружные углы стен

Кривые наружные углы – это результат спешной работы строителей. Для их выравнивания нужно сначала определить степень кривизны. Еще одной причиной выравнивания являются частые удары острыми и тяжелыми предметами.

Для выравнивания применят материалы и инструменты. Также обязателен уровень.

Что потребуется

Для работы нужен будет перфорированный уголок, шпаклевочная или штукатурная смесь на основе гипса, грунтовка, обычный и угловой шпатели.

Работу проводить несложно, если «под рукой» есть всё необходимое. Даже самая кривая стыковочная поверхность создаётся под 90 градусов, не прилагая много усилий и времени.

Как выровнять углы стен под 90 градусов с помощью уголка

Наружный угол выровнять легче, чем внутренний. Для этого применяют перфорированный металлический уголок.

Сначала поверхность очищают и покрывают грунтовкой.
После выявляют степень кривизны.
На угол с двух сторон накладывают штукатурный или шпаклевочный гипсовый раствор.
В него вдавливают и выравнивают при помощи уровня уголок.
Дают время для застывания раствора. Всю лишнюю массу убирают. По сторонам выравнивают шпателем.
После высыхания наждачной бумагой надо убрать излишки и тонким слоем наложить еще раз раствор. При этом работу выполняют аккуратно, чтобы не было бугорков.

Окончательный шаг – зашкуривание наждачной бумагой и покрытие грунтовкой для финишной отделки.

Перфорированный уголок не только выровняет угол на 90 градусов, но и защитит поверхность от ударов.

Как выставить угол 90 градусов при штукатурке стен

Если угол имеет большой процент кривизны, тогда применяют иной метод. На стене от стыка в противоположной стороне выставляют маяк. От него в сторону идет равнение. Таким образом, равняют примыкающую стену. Ровные стены образуют угол 90 градусов. Окончательно выравнивание производят угловым шпателем.

Способы, как проверить угол 90 градусов между стенами внутри и снаружи

Есть несколько способов проверить насколько угол ровный. Итак:

Угольником – самый простой способ.
Второй способ – создание уголка из профиля. От угла по одной стене отмерить 30,60,90 см. Длина одной стороны профиля будет равна 90. В другую сторону на смежной стене отложить 30,60,90,120 см. Длина второй стороны профильного уголка будет равна 120 см. От одной точки, где отложено 90 до другой точки 120 должно быть расстояние 150 см. Стороны профиля соединяют шурупами под 90 градусов. Края соединяют еще одним куском профиля равным 150 см. Этим уголком измеряют внутренний угол в комнате в нескольких местах.
Внешний угол измеряют по такой же схеме, только все отметки отмечают на полу. То есть. От внешнего угла на полу надо отступить длину кратную 4. Допустим, 1,6 метра. Её откладывают вдоль одной стены. Далее, вдоль другой стены надо отложить 1,2 метра. Между конечными точками должно быть расстояние 2 метра. Если это так, тогда угол имеет 90 градусов. Если нет, тогда следует применить выравнивание.

Перед тем как начать выравнивать стыки стен надо выяснить насколько они имеют отклонение, кривизну. ДЛ выравнивания применяют как гипсокартон, фанеру, так и обычную шпаклевку, и перфорированные уголки. Для выведения точного красивого угла надо запастись материалами, инструментами и немного математических знаний – теорема Пифагора.

Полезное видео

Кто занимается самостоятельным строительством знает, что до начала постройки сооружения надо своими руками разметить фундамент. Здесь рассмотрен случай начала работ по возведению свайного винтового фундамента на участке по ряду причин садоводческого характера не очищенного от полезных растений. Это затрудняло работы по разметке будущего фундамента, но эти трудности легко были преодолены с помощью простого приспособления по выставлению прямых углов.

Как сделать разметку фундамента своими руками

Обычно разметка фундамента в самостоятельном строительстве делается на глаз при помощи рулетки. Сначала выставляются столбики разметки углов стен на расстояниях длины и ширины будущей постройки. Потом делается замер диагоналей полученного прямоугольника и начинается процесс перестановки двух смежных столбов до выравнивания замеров диагоналей. По основам геометрии прямоугольником является фигура у которой две диагонали равны между собой. Но именно из за посадок замер диагоналей в процессе подгонки и был затруднен. Посадки мешали натянуть рулетку и затеняли лазер дальномера. Но эту трудность можно преодолеть.

1. До начала работ надо обладать минимальными знаниями геометрии и знать решение теоремы Пифагора:). Напомню теорему. Квадрат гипотенузы равен сумме квадратов катетов в прямоугольном треугольнике.

2. Натянем между двумя колышками шнур обозначающий первую стену фундамента. Если сторона фундамента, например, равна 6 метрам, то расстояние между колышками должно быть не меньше 8 метров.

3. Сделаем приспособление для выставления прямого угла на местности. Для этого надо приобрести упаковку обязательно нетянущегося шнура или применить стальной тросик. Всего потребуется около 13 метров шнура.

4. Связываем сложенные вместе концы шнура так, чтобы длина полученной петли равнялась 6 метрам. Точность завязывания и выставления размера важна.

5. Берем перманентный фломастер и от центра узла при помощи рулетки делаем отметки на расстоянии 3 метра в одну сторону и на расстоянии 4 метра в другую сторону. Так мы получили веревочный прямоугольный треугольник. Это изобретение позволит вычислить направление угла 90° простым растягиванием треугольника.

Разметка первой стены Набор для лайфхака Стороны треугольника

6. Для работы на местности нам потребуются тонкие деревянные колышки или куски тонкой арматуры.

7. Устанавливаем один колышек для обозначения угла фундамента на линии разметки сделанной ранее в п.2.

8. Берем веревочный лайфхак. Узел помещаем на колышке обозначающем угол и растягиваем стороны веревочного треугольника вбивая первый колышек на расстоянии 4 метра в разметки стены п.2., перегиб шнура должен быть на метке фломастера 4 метра.

9. Выставляем колышек на метке 3 метра. Одна сторона прямоугольника параллельна разметке первой стены, а вторая сторона указывает направление разметки под углом 90° для второй стены. Теорема Пифагора в действии — смотри фото.

Куски арматуры Колышек основания прямого угла Веревочный треугольник

10. Натягиваем разметочный шнур для второй стены, параллельно стороне треугольника.

11. Проводим аналогичные действия для разметки третьей стены.

12. Обозначаем на разметке длины второй и третьей стены и проводим контроль на одном из углов правильности направления четвертой стены. Если длина стены в разметке составила 6 метров и ее направление пересекло точки разметки стен два и три, то можно сказать, что замер диагоналей даст равный результат. Если схождения не получилось, проверьте еще раз правильность установки разметки.

Выставление разметки 2-й стены Шнур второй стены

К ачественный ремонт и отделка подразумевает хорошую геометрию помещения. Без выверенной геометрии, хотя бы в самых нужных местах, хороший ремонт сделать не удастся. Здесь я расскажу как сделать угол 90 градусов между стенами своими руками и о том, где он действительно необходим. Так же можно почитать статью по ссылке → и как проверить правильность геометрии, и что будет если геометрия нарушена.

Содержание:
1.
2.
2.1
2.2
3.
4.
5.
5.1
6.
7.

Где нужен угол 90 градусов между стенами

в том углу, где будет висеть/стоять кухонная мебель,
и в ванной комнате, где будет стоять сама ванна, в двух смежных углах (или в одном, если душевая кабина стоит в углу). Или по всем 4-м углам ванной, поскольку там будут стоять раковина, стиральная машина и т.п.

В остальных случаях — всё на желание заказчика или человека, осуществляющего ремонт своими силами.

Чем проверять и выставлять углы

Угол легко проверить строительным угольником, можно приобрести в магазине, если собираетесь выводить углы, он будет вам необходим.

Просто прислоняем угольник к внутреннему углу. Наружные углы мы пока рассматривать не будем, ради понимания самого процесса. После понимания как выравнивать внутренние углы под 90 градусов своими руками, внешние для вас проблем не составят.

Смотрим, что получается. Если всё нормально, зазоров между угольником нет, то расслабьтесь. Если зазор превышает 5 мм, то следует насторожиться и узнать как выровнять такой угол в прямой, что бы и ванна и шкафы висели хорошо. Дело в том, что зазор в 5 мм под небольшим, пускай полуметровым (в длину хотя бы одной грани) угольником, на всю длину стены оказывается довольно крупным и в конце стены может достичь и 5 см.

Делаем угольник самостоятельно

Угольник можно соорудить и самостоятельно, причём любого размера. Удобнее всего делать такой угольник из гипсокартонных профилей 27*28 мм (жёстких или полужёстких).

Пользуемся пра́вилом египетского треугольника, при котором: если катеты угла равны 3 и 4 частям, а гипотенуза 5 частям, то угол будет прямоугольным (прямой угол между катетами).

Надрезаем и сгибаем нужной длины профиль посредине (стороны нашего угольника не обязательно должны быть равны 3 и 4 определённым нами частям, пра́вило нужно лишь для того, чтобы сделать прямой угол). Сгибаем, принимаем за 1 часть, к примеру, 30 см. Чем больше вы сделаете часть, тем «прямее» получится угол.

Как найти угол в прямоугольном треугольнике

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно или несколько ваших авторских прав, сообщите нам об этом, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

Как найти меру угла

Два луча с одной и той же конечной точкой создают угол. Точка, в которой они пересекаются, называется вершиной. Угол образует часть воображаемого круга.А поскольку круги измеряют 360 градусов, вы можете найти угол, образованный лучами. Вот несколько вещей, которые вы должны знать о том, как найти величину угла.

Четыре типа углов

Есть четыре типа углов. Знание разницы поможет вам оценить размер угла. Вот четыре типа углов и размеров, которые помогут вам классифицировать каждый из них.

Прямой угол (180 градусов)

Острый угол (менее 90 градусов)

Прямой угол (90 градусов)

Тупой угол (более 90 градусов, но менее 180 градусов)

Использование транспортира

Лучший способ измерить угол — использовать транспортир.Для этого вы начнете с выстраивания одного луча вдоль линии под углом 0 градусов на транспортире. Затем совместите вершину с серединой транспортира. Следуйте по второму лучу, чтобы определить угол с точностью до градуса.

Углы в треугольниках

Треугольники получили свое название от трех углов, которыми они обладают. Эти три угла в сумме должны составлять 180 градусов. Часто у вас есть измерения двух углов. Однако вам придется вычислить размер третьего угла.Используемое уравнение:

угол A + угол B + угол C = 180 градусов.

Например, у вас есть следующий треугольник. Что такое измерение угла C?

Если вы подставите эти числа в уравнение, вы получите следующее уравнение:

Углы в четырехугольниках

Квадраты и прямоугольники имеют четыре прямых угла. Если сложить углы, получится 90 + 90 + 90 + 90 = 360. Четырехугольник также имеет четыре угла.Следовательно, углы формы составляют в сумме 360 градусов, даже если нет прямых углов. Чтобы определить недостающий угол четырехугольника, вы можете использовать следующее уравнение:

угол A + угол B + угол C + угол D = 360 градусов.

Посмотрите следующий пример. Можете ли вы определить недостающий угол в этом четырехугольнике?

Чтобы найти недостающий угол, подставьте измерения угла в уравнение:

Независимо от того, работаете ли вы с лучом, треугольником или четырехугольником, есть методы, которые вы можете использовать для обнаружения недостающего измерения угла. .Если вам интересно, как найти угол на луче, треугольнике или четырехугольнике, попробуйте использовать транспортир или уравнения, которые мы обсуждали. Они должны работать и помочь вам немного облегчить жизнь!

О Джейми Гудвине

Джейми окончил Университет Бригама Янга в Айдахо по специальности «Английский язык». Она провела несколько лет, обучая и обучая учеников начальной, средней школы и колледжа. В настоящее время она работает писателем по контракту и разработчиком учебных программ для онлайн-курсов.В свободное время она любит бегать и проводить время со своими мальчиками!

Что такое угол 90 градусов и почему он важен?

Вам дают транспортир и приказывают отмерить 90 градусов. Но что такое градус и что такое угол в 90 градусов? Что ж, градус — это то, как мы измеряем углы — 360 градусов обозначают полный круг вращения. Угол в 90 градусов также известен как прямой угол.

Различные типы углов

В тригонометрии разные типы углов определяются и называются по их размерам.Прямой угол — 90 градусов. Острый угол — это угол менее 90 градусов. Тупой угол — это угол более 90 градусов.

Эти углы также помогают идентифицировать различные типы треугольников. Прямоугольный треугольник — это любой треугольник, который содержит угол 90 градусов или прямой угол. Тупой треугольник — это любой треугольник, который содержит тупой угол (больше 90 градусов).

Острый треугольник — это треугольник с ровно тремя острыми углами (менее 90 градусов).Почему именно три? Потому что прямоугольный и тупой треугольники также содержат по крайней мере еще один острый угол.

Почему 90-градусные углы имеют значение?

Многоугольники, особенно треугольники, которые содержат угол 90 градусов, обладают некоторыми особыми свойствами.

Рассмотрим прямоугольные треугольники. Теорема Пифагора, например, говорит нам, что сумма квадратов длин сторон прямоугольного треугольника всегда равна квадрату гипотенузы. Это неверно для равнобедренного, равностороннего или любого другого треугольника, который не имеет угла 90 градусов.

Две прямые, пересекающиеся под углом 90 градусов, также называются перпендикулярными. Перпендикулярные линии находят множество применений, когда дело доходит до геометрических доказательств и анализа различных вершин и углов. Они также полезны для обеспечения правильной прямолинейности и выравнивания в таких областях, как строительство или покраска.

Что такое прямой угол в радианах?

Когда мы говорим об угловых мерах в геометрии, мы можем использовать градусы или радианы. Радианы измеряются в единицах пи.Два радиана пи эквивалентны 360 градусам. Следовательно, угол в 90 градусов или прямой угол равен пи / 2 радиана.

Что такое угол 90 градусов?

Градусы — наиболее распространенная единица измерения геометрических углов, хотя для измерения углов треугольника можно использовать и радианы, и градусы. Если вы работаете с тригонометрическими функциями, такими как синус или косинус, работать с радианами проще.

Однако, когда речь заходит о практических приложениях, вы чаще слышите «угол 90 градусов» или «прямой угол».Вы найдете прямые углы, используемые во всех сферах жизни, от строительства до организации, искусства, вождения и не только.

Дополнительные домашние задания по математике

Три типа геометрических доказательств, которые вам необходимо знать

Понимание двухусловного оператора

Как найти сумму конечной геометрической последовательности

Вопрос: Как измерить угол в 90 градусов без транспортира?

Что такое угол 45%?

Когда два луча пересекаются в одной конечной точке, они образуют угол.

…

Угол можно измерить с помощью транспортира, а угол измерения 90 градусов называется прямым углом.

Под прямым углом два плеча перпендикулярны друг другу.

Когда прямой угол разделен на две равные части, каждый угол составляет 45 °.

Угол в 90 градусов прямой?

В геометрии существует три типа углов: острый угол — угол от 0 до 90 градусов. Прямой угол — угол 90 градусов. … Прямой угол — угол 180 градусов.

Т-образные углы в архитектуре Используйте Т-образный квадрат для рисования горизонтальных линий и измерения углов 90 градусов по отношению к этим линиям. Используйте регулируемый треугольник для измерения углов от 0 до 90 градусов, поместив его на горизонтальную ось и отрегулировав откидной край, пока он не совпадет с наклонной линией, которую вы хотите измерить.

Как называется угол 120 градусов?

Число градусов Тип углаПричина60Острый (больше) 90 градусов170Открыть> (больше) 90 градусов90Правый угол = 90 градусов3 больше строк

Как измерить угол без транспортира?

Как рассчитать углы без транспортира Отметьте две точки на линии, противоположной углу.Измерьте линию, воспользуйтесь формулой синуса и вычислите угол.

Как построить угол в 90 градусов без транспортира?

Мы можем построить угол 90 °, разделив прямой угол пополам или выполнив следующие шаги. Шаг 1: Нарисуйте руку PA. Шаг 2: Поместите точку циркуля в точку P и нарисуйте дугу, которая пересекает руку в точке Q. Шаг 3: Поместите точку циркуля в точку Q и нарисуйте дугу радиуса PQ, которая пересекает дугу, нарисованную на шаге 2, в точке R. Другие элементы…

Транспортир Транспортир — это наиболее распространенное устройство, используемое для измерения углов.

Как выглядит угол 90?

В геометрии и тригонометрии прямой угол — это угол, равный точно 90 ° (градусам), что соответствует четверти оборота. … Этот термин образован от латинского angulus rectus; здесь rectus означает «вертикальный», имея в виду вертикальный перпендикуляр к горизонтальной базовой линии.

«+» ipt> «;

Измерение углов

Понятие угла

Понятие угла — одно из важнейших понятий в геометрии.Понятия равенства, суммы и разности углов важны и используются во всей геометрии, но предмет тригонометрии основан на измерении углов .

Есть две обычно используемые единицы измерения углов. Более знакомая единица измерения — это градусы. Круг делится на 360 равных градусов, так что прямой угол равен 90 °. Пока мы будем рассматривать только углы от 0 ° до 360 °, но позже, в разделе о тригонометрических функциях, мы будем рассматривать углы больше 360 ° и отрицательные углы.

Градусы можно разделить на минуты и секунды, но это деление не так универсально, как раньше. Каждый градус делится на 60 равных частей, называемых минутами. Итак, семь с половиной градусов можно назвать 7 градусами и 30 минутами, записанными как 7 ° 30 ‘. Каждая минута далее делится на 60 равных частей, называемых секунд, и, например, 2 градуса 5 минут 30 секунд записывается как 2 ° 5 ’30 «. Деление градусов на минуты и угловые секунды аналогично делению на часы в минуты и секунды.

Части градуса теперь обычно обозначаются десятичной дробью. Например, семь с половиной градусов теперь обычно пишут как 7,5 & deg.

Когда один угол нарисован на плоскости xy для анализа, мы нарисуем его в стандартной позиции с вершиной в начале координат (0,0), одна сторона угла вдоль x ось, а другая сторона выше оси x .

Радианы

Другое распространенное измерение углов — радианы.Для этого измерения рассмотрим единичный круг (круг радиуса 1), центр которого является вершиной рассматриваемого угла. Затем угол отсекает дугу окружности, и длина этой дуги является мерой угла в радианах. Легко переходить между градусами и радианами. Окружность всего круга равна 2 π , следовательно, 360 ° равняется 2 π радиан. Следовательно,

1 ° равняется π /180 радиан

а также

1 радиан равен 180/ π градусов

Большинство калькуляторов можно настроить на использование углов, измеряемых в градусах или радианах.Убедитесь, что вы знаете, в каком режиме работает ваш калькулятор.

Краткая заметка по истории радианов

Хотя слово «радиан» было придумано Томасом Мьюиром и / или Джеймсом Томпсоном около 1870 года, математики долгое время измеряли углы таким способом. Например, Леонард Эйлер (1707–1783) в своей работе Elements of Algebra явно сказал, что углы следует измерять по длине дуги, отрезанной в единичной окружности.Это было необходимо, чтобы дать его знаменитую формулу, включающую комплексные числа, которая связывает функции знака и косинуса с экспоненциальной функцией. e ^iθ = cos θ + i sin θ

где θ — это то, что позже было названо измерением угла в радианах. К сожалению, объяснение этой формулы выходит далеко за рамки этих заметок. Но для получения дополнительной информации о комплексных числах см. Мой Краткий курс комплексных чисел.

Радианы и длина дуги

Альтернативное определение радианов иногда дается в виде отношения. Вместо того, чтобы брать единичную окружность с центром в вершине угла θ , возьмите любую окружность с центром в вершине угла. Тогда радианная мера угла — это отношение длины вытянутой дуги к радиусу r окружности. Например, если длина дуги равна 3, а радиус круга равен 2, тогда радианная мера равна 1.5.

Причина, по которой это определение работает, заключается в том, что длина вытянутой дуги пропорциональна радиусу круга. В частности, определение в терминах отношения дает ту же цифру, что и приведенная выше с использованием единичного круга. Однако это альтернативное определение более полезно, поскольку вы можете использовать его для соотнесения длин дуг с углами. Длина дуги равна радиусу r, умноженному на угол θ , где угол измеряется в радианах.

Например, дуга θ = 0,3 радиана в окружности радиуса r = 4 имеет длину 0,3 умноженную на 4, то есть 1,2.

Радианы и площадь сектора

Сектор круга — это часть круга, ограниченная двумя радиусами и дугой окружности, соединяющей их концы. Площадь этого сектора легко вычислить по радиусу r круга и углу θ между радиусами, если он измеряется в радианах.Так как площадь всего круга составляет πr ², а сектор относится ко всей окружности, так как угол θ равен 2 π , поэтому

Общие углы

Ниже приведена таблица общих углов для измерения в градусах и радианах. Обратите внимание, что измерение в радианах дано в терминах π . Его, конечно, можно было бы дать десятичной дроби, но радианы часто появляются с коэффициентом π .

Уголок	градусов	Радианы
	90 °	π /2
	60 °	π /3
	45 °	π /4
	30 °	π /6

Упражнения

Эдвин С.Кроули написал книгу Тысяча упражнений в плоской и сферической тригонометрии, Университет Пенсильвании, Филадельфия, 1914. Задачи этого короткого курса взяты из этого текста (но не все 1000 из них!). пять знаков точности, поэтому студентам пришлось потрудиться, чтобы решить их, и они использовали таблицы логарифмов, чтобы помочь в умножении и делении. Студенты должны были уметь пользоваться таблицей синус-косинусов, таблицей касательных, таблицей логарифмов, таблицей log-sin-cos и таблицей log-tan.Теперь мы можем пользоваться калькуляторами! Это означает, что вы можете сосредоточиться на концепциях, а не на трудоемких вычислениях.

Кроули использовал не десятичные дроби для дробей градуса, а минуты и секунды.

Каждый комплекс упражнений включает в себя, во-первых, формулировку упражнений, во-вторых, некоторые подсказки для решения упражнений, а в-третьих, ответы на упражнения.

1. Выразите следующие углы в радианах.
(а). 12 градусов, 28 минут, то есть 12 ° 28 ‘.
(б). 36 ° 12 ‘.

2. Сократите следующие числа радианов до градусов, минут и секунд.
(а). 0,47623.
(б). 0,25412.

3. Учитывая угол a и радиус r, , чтобы найти длину проходящей дуги.
(а). a = 0 ° 17 ’48 дюймов, r = 6,2935.
(б). a = 121 ° 6 ’18 дюймов, r = 0,2163.

4. Учитывая длину дуги l и радиус r, , чтобы найти угол, стянутый в центре.
(а). l = 0,16296, r = 12,587.
(б). l = 1,3672, r = 1,2978.

5. Зная длину дуги l и угол a , который она проходит в центре, найти радиус.
(а). a = 0 ° 44 ’30 дюймов, l = 0,032592.
(б). a = 60 ° 21 ‘6 дюймов, l = 0,4572.

6. Найдите длину с точностью до дюйма дуги окружности 11 градусов 48,3 минуты, если радиус составляет 3200 футов.

7. Кривая железной дороги образует дугу окружности 9 градусов 36,7 минут, радиус до центральной линии пути составляет 2100 футов. Если калибр 5 футов, найдите разницу в длине двух рельсов с точностью до полудюйма.

9. На сколько можно изменить широту, идя на север на одну милю, если предположить, что Земля представляет собой сферу радиусом 3956 миль?

10. Вычислите длину в футах одной угловой минуты на большом круге Земли. Какова длина дуги в одну секунду?

14. На окружности радиусом 5,782 метра длина дуги составляет 1,742 метра. Какой угол он образует в центре?

23. Воздушный шар, известный как 50 футов в диаметре, сужается к глазу под углом 8 1/2 минут.Как далеко это?

Подсказки

1. Чтобы преобразовать градусы в радианы, сначала преобразуйте количество градусов, минут и секунд в десятичную форму. Разделите количество минут на 60 и прибавьте к количеству градусов. Так, например, 12 ° 28 ‘равно 12 + 28/60, что равно 12,467 °. Затем умножьте на π и разделите на 180, чтобы получить угол в радианах.

2. И наоборот, чтобы преобразовать радианы в градусы, разделите на π и умножьте на 180.Таким образом, 0,47623, деленное на π и умноженное на 180, дает 27,286 °. Вы можете преобразовать доли градуса в минуты и секунды следующим образом. Умножьте дробь на 60, чтобы получить количество минут. Здесь 0,286 умножить на 60 равно 17,16, поэтому угол можно записать как 27 ° 17,16 ‘. Затем возьмите любую оставшуюся долю минуты и снова умножьте на 60, чтобы получить количество секунд. Здесь 0,16 умножить на 60 равно примерно 10, поэтому угол также можно записать как 27 ° 17 ’10 «.

3. Чтобы найти длину дуги, сначала преобразуйте угол в радианы. Для 3 (a) 0 ° 17’48 «составляет 0,0051778 радиана. Затем умножьте его на радиус, чтобы найти длину дуги.

4. Чтобы найти угол, разделите его на радиус. Это дает вам угол в радианах. Их можно преобразовать в градусы, чтобы получить ответы Кроули.

5. Как упоминалось выше, радиан умноженный на радиус = длина дуги, поэтому, используя буквы для этой задачи, ar = l, , но a необходимо сначала преобразовать из градуса в радиан .Итак, чтобы найти радиус r, сначала преобразует угол a в радианы, а затем разделит его на длину l дуги.

6. Длина дуги равна радиусу, умноженному на угол в радианах.

7. Помогает нарисовать фигуру. Радиус внешнего рельса равен 2102,5, а радиус внутреннего рельса — 2097,5.

9. У вас есть круг радиусом 3956 миль и дуга этого круга длиной 1 милю.Какой угол в градусах? (Средний радиус Земли был известен довольно точно в 1914 году. Посмотрим, сможете ли вы узнать, каким, по мнению Эратосфена, был радиус Земли, еще в III веке до н. Э.)

10. Угловая минута равна 1/60 градуса. Преобразовать в радианы. Радиус — 3956. Какова длина дуги?

14. Поскольку длина дуги равна радиусу, умноженному на угол в радианах, отсюда следует, что угол в радианах равен длине дуги, деленной на радиус.Радианы легко преобразовать в градусы.

23. Представьте, что диаметр воздушного шара является частью дуги окружности с вами в центре. (Это не совсем часть дуги, но довольно близко). Длина дуги составляет 50 футов. Вы знаете угол, так каков радиус этого круга?

Ответы

1. (а). 0,2176. (б). 0,6318.

2. (а). 27 ° 17 ’10 «. (B). 14,56 ° = 14 ° 33,6′ = 14 ° 33’36».

3. (а). 0,03259 (б). 2,1137 умножить на 0,2163 равно 0,4572.

4. (а). 0,16296 / 12,587 = 0,012947 радиан = 0 ° 44 ’30 дюймов.
(б). 1,3672 / 1,2978 = 1,0535 радианы = 60,360 ° = 60 ° 21,6 ‘= 60 ° 21’ 35 «.

5. (а). л / год = 0,032592 / 0,01294 = 2,518.
(б). л / год = 0,4572 / 1,0533 = 0,4340.

6. ra = (3200 ‘) (0.20604) = 659,31 ‘= 659’ 4 дюйма.

7. Угол a = 0,16776 радиана. Разница в длине составляет 2102,5 a — 1997,5 a , что составляет 5 a. Таким образом, ответ составляет 0,84 фута, что с точностью до дюйма составляет 10 дюймов.

9. Угол = 1/3956 = 0,0002528 радиан = 0,01448 ° = 0,8690 ‘= 52,14 дюйма.

10. Одна минута = 0,0002909 радиан. 1.15075 миль = 6076 футов.Следовательно, одна секунда будет соответствовать 101,3 фута.

14. a = л / об = 1,742 / 5,782 = 0,3013 радиан = 17,26 ° = 17 ° 16 ‘.

23. Угол a равен 8,5 ‘, что составляет 0,00247 радиана. Таким образом, радиус равен r = л / год = 50 / 0,00247 = 20222 ‘= 3,83 мили, почти четыре мили.

Насчет цифр точности.

Кроули старается давать свои ответы примерно с той же точностью, что и данные в вопросах.Это важно, особенно сейчас, когда у нас есть калькуляторы. Например, в задаче 1 точка отсчета равна 12 ° 28 ‘, что соответствует примерно четырем знакам точности, поэтому ответ 0,2176 также должен быть дан только с точностью до четырех знаков. (Обратите внимание, что ведущие нули не учитываются при вычислении цифр точности.) Ответ 0,21758438 предполагает восемь цифр точности, и это может ввести в заблуждение, поскольку данная информация не была такой точной.

Другой пример см. В задаче 3 (a). Данные 0 ° 17’48 «и 6.2935 с точностью до 4 и 5 знаков соответственно. Следовательно, ответ должен быть дан только с точностью до 4 цифр, поскольку ответ не может быть более точным, чем наименее точные данные. Таким образом, ответ, который может дать калькулятор, а именно 0,032586547, следует округлить до четырех цифр (не включая ведущие нули) до 0,03259.

Хотя окончательные ответы должны быть выражены с соответствующим числом цифр точности, вы все равно должны сохранять все цифры для промежуточных вычислений.

Типы углов — объяснения и примеры

В природе существуют разные типы углов , , и каждый из них имеет большое значение в нашей повседневной жизни.

Например, , архитекторы и инженеры используют углы при проектировании машин, зданий, дорог и мостов.

В спорте спортсмены используют углы для улучшения своих результатов. Например, человек должен вращаться с диском под определенным углом, чтобы бросить его на короткое расстояние.В футболе вы должны использовать определенный угол, чтобы передать мяч следующему игроку.

Плотники и ремесленники также используют углы для изготовления таких предметов, как диваны, столы, стулья, ведра и т. Д. Художники используют углы для набросков портретов и картин. Модельеры также используют ракурсы, чтобы подобрать лучшие наряды. По этим причинам необходимо изучить различные типы углов.

(Чтобы пройти базовое объяснение углов, вы можете обратиться к предыдущей статье «Углы.”)

Различные типы углов

Углы классифицируются на основе:

Классификация углов на основе их величины

Существует семь типов углов, основанных на их градусном измерении. К ним относятся:

нулевые углы
острые углы
прямые углы
тупые углы
прямые углы
углы отражения
полный угол

— нулевой угол

нулевой угол (0 °) — это угол формируется, когда оба плеча уголка находятся в одном и том же положении.

Иллюстрация:

∠ RPQ = 0 ° (нулевой угол)

— Острый угол

Острый угол — это угол, который больше 0 °, но меньше 90 °. Типичные примеры острых углов: 15 °, 30 °, 45 °, 60 ° и т. Д.

∠ XYZ больше 0 °, но меньше 90 ° (острый угол)

— Угол 90 градусов

A Угол 90 градусов, также известный как прямой угол, — это угол, размер которого равен 90 °, и называется прямым углом. Прямые углы изображаются в виде небольшой квадратной рамки между плечами угла.

Иллюстрация:

∠ ABC = 90 ° (прямой угол)

В следующем разделе (Треугольники) будет целая статья о прямоугольных треугольниках.

— Тупой угол

Тупой угол — это тип угла, градусы которого больше 90 °, но меньше 180 °. Примеры тупых углов: 100 °, 120 °, 140 °, 160 °, 170 ° и т. Д.

∠ PQR — тупой угол, потому что он меньше 180 ° и больше 90 °.

— Прямой угол

Как следует из названия, прямой угол — это угол, размер которого равен 180 ° (прямая линия)

Иллюстрация:

∠ XYZ = 180 ° (прямой угол)

— Reflex Угол

Углы отражения — это углы, градусы которых больше 180 °, но меньше 360 °.Общие примеры углов рефлекса: 200 °, 220 °, 250 °, 300 °, 350 ° и т. Д.

Иллюстрация:

∠ PQR больше 180 °, но меньше 360 °

— Полный угол

Полный угол равен 360 °. 1 оборот равен 360 °.

Иллюстрация:

Классификация углов на основе вращения

В зависимости от направления вращения углы можно разделить на две категории, а именно;

Положительные углы
Отрицательные углы

Положительные углы

Положительные углы — это типы углов, измерения которых проводятся против часовой стрелки от основания.

Отрицательные углы

Отрицательные углы измеряются по часовой стрелке от основания.

Другие типы углов

Помимо рассмотренных выше углов, существуют другие типы углов, известные как парные углы. Их называют парными углами, потому что они появляются парами, чтобы показать определенное свойство. Это:

Соседние углы имеют одинаковую вершину и плечо.
Дополнительные углы: парные углы, которые в сумме составляют 90 °.
Дополнительные углы: парные углы, сумма углов которых равна 180º.
Вертикально противоположные углы. Вертикально противоположные углы равны.
Альтернативные внутренние углы: Альтернативные внутренние углы — это парные углы, образующиеся, когда линия пересекает две параллельные линии. Чередующиеся внутренние углы всегда равны друг другу.
Альтернативные внешние углы : Альтернативные внешние углы — это просто вертикальные углы альтернативных внутренних углов. Альтернативные внешние углы эквивалентны.
Соответствующие углы : Соответствующие углы — это парные углы, образующиеся, когда прямая пересекает пару параллельных прямых. Соответствующие углы также равны друг другу.

Мы видели краткий обзор различных типов углов. Далее мы увидим подробные статьи о наиболее распространенных типах углов (Дополнительные углы, Дополнительные углы и т. Д.).

Предыдущий урок | Главная страница | Следующий урок

Дополнительные углы — объяснение и примеры

Что такое дополнительный угол?

Дополнительные углы — это парные углы с суммой 90 градусов. Говоря о дополнительных углах, всегда помните, что углы появляются парами. Один угол является дополнением другого угла.

Хотя прямой угол равен 90 градусам, его нельзя назвать дополнительным, потому что он не попадает в пары. Это просто полный угол. Три или более углов, сумма которых равна 90 градусам, также нельзя назвать дополнительными углами.

Дополнительные углы всегда имеют положительную величину. Он состоит из двух острых углов размером менее 90 градусов.

Общие примеры дополнительных углов:

Два угла по 45 градусов каждый.
Углы размером 30 и 60 градусов.
Углы измерения 1 градус и 89 градусов.

Дополнительным углом могут быть смежные углы.

Например, ,

∠ STA = 65 градусов и ∠ATR = 25 градусов являются смежными дополнительными углами.

У нас также могут быть дополнительные углы, которые не примыкают друг к другу.

Например, ,

∠ DGO = 20 градусов и ∠ ODG = 70 градусов — это пары дополнительных углов, которые не примыкают друг к другу.

Еще одно важное свойство , которое следует отметить в отношении дополнительных углов , заключается в том, что два дополнительных угла не обязательно должны быть на одной и той же фигуре.

Пока углы складываются в 90 градусов, они дополняют друг друга.
Например:

Два угла на разных рисунках выше дополняют друг друга.

∠ABC + ∠ XYZ = 90 градусов

Как найти дополнительный угол?

Поскольку мы знаем, что дополнительные углы складываются в 90 градусов, мы можем легко вычислить значение любого угла, вычтя данные углы из 90 градусов.

Пример 1

Рассчитайте дополнительный угол 33 °.

Решение

Вычтите заданный угол из 90 °.

90 ° — 33 °

= 57 °

Следовательно, дополнение до 33 ° равно 57 °

Пример 2

Определите недостающий угол на следующем рисунке

Решение

∠ABC + ∠ACB + 90 ° = 180 °

Следовательно, BAC + ∠ACB = 90 ° (дополнительные углы)

∠BAC + 43 ° = 90 °

∠BAC = 90 ° — 43 °

∠ BAC = 47 °

Пример 3

Найдите дополнение 27 ° 20 ′

Решение

90 ° — 27 ° 20 ′

= 89 ° 60 ′ — 27 ° 20 ′

= 62 ° 40 ′

Следовательно, дополнение к 27 ° 20 ′ равно 62 ° 40 ′

Пример 4

Найдите угол, который на 46 ° меньше его дополнения.

Решение

Пусть x будет неизвестным углом.

(90 — x) — x = 46 °

90 — x — x = 46 °

90 — 2x = 46 °

90 — 90 — 2x = 46 ° — 90

-2x = 46 ° — 90

-2x = -44 °

2x = 44 °

x = 44/2

x = 22 °

Следовательно, 90-22 = 68 °

Пример 5

Если разница между двумя дополнительными составляет 18 градусов, найдите углы.

Решение

Пусть меньший угол будет x градусов, а больший угол будет (90 — x) °.

(90 ° — x) — x = 18 °

90 ° — 2x = 18 °

x = 72 ° / 2

x = 36 °

90 ° — x

= 90 ° — 36 °

= 54 °.

Таким образом, два дополнительных угла равны 36 ° и 54 °.

Пример 6

Рассчитайте значение x на следующем рисунке:

Решение

⟹ (2x — 7) ° + (x + 4) ° = 90 °

⟹2x + x — 7 ° + 4 ° = 90 °

⟹ 3x — 3 ° = 90 °

⟹ 3x — 3 ° + 3 ° = 90 ° + 3 °

⟹ 3x = 93 °

⟹ x = 93 ° / 3

⟹ x = 31 °

Пример 7

Найдите дополнительный угол 2/3 от 90 градусов.

Решение

⟹ 90 ° x 2/3 = 60 °

⟹ 90 ° — 60 ° = 30 °

Следовательно, угол дополнения равен 30 °

Пример 8

Определите дополнительный угол (x + 10) °.

Раствор

⟹ (x + 10) ° = 90 ° — (x + 10) °

= 90 ° — 10 ° — y °

= (80 — x) °

Пример 9

Два дополнительных угла таковы, что один из углов в два раза превышает сумму другого угла плюс 3 градуса.Найдите два дополнительных угла.

Решение

Пусть два угла равны x и y градусам.

⟹ x + y = 90 °

Один из углов равен удвоенной сумме другого угла плюс 3 градуса.

⟹ x = 2 (y + 3)

⟹ x = 2y + 6

Теперь решим два одновременных уравнения подстановкой.

⟹ 2y + 6 + y = 90

⟹ 3y + 6 = 90

⟹ 3y = 84

⟹ y = 28

⟹ x = 2 (28) + 6

⟹ x = 56 + 6

⟹ x = 62

Предыдущий урок | Главная страница | Следующий урок .