Построение с помощью циркуля и линейки — Википедия
Построе́ния с по́мощью ци́ркуля и лине́йки — раздел евклидовой геометрии, известный с античных времён.
В задачах на построение циркуль и линейка предполагаются идеальными инструментами, в частности:
- Линейка не имеет делений и имеет сторону бесконечной длины, но только одну.
- Циркуль может иметь какой угодно большой или малый раствор (то есть может чертить окружность произвольного радиуса).
 Разбиение отрезка пополам
Разбиение отрезка пополамЗадача на бисекцию. С помощью циркуля и линейки разбить данный отрезок AB на две равные части. Одно из решений показано на рисунке:
- Циркулем проводим окружности с центром в точках A и B радиусом AB.
- Находим точки пересечения P и Q двух построенных окружностей (дуг).
- По линейке проводим отрезок или линию, проходящую через точки
- Находим искомую середину отрезка AB — точку пересечения AB и PQ.
В задачах на построение рассматривается множество следующих объектов: все точки плоскости, все прямые плоскости и все окружности плоскости. В условиях задачи изначально задается (считается построенными) некоторое множество объектов. К множеству построенных объектов разрешается добавлять (строить):
- произвольную точку;
- произвольную точку на заданной прямой;
- произвольную точку на заданной окружности;
- точку пересечения двух заданных прямых;
- точки пересечения/касания заданной прямой и заданной окружности;
- точки пересечения/касания двух заданных окружностей;
- произвольную прямую, проходящую через заданную точку;
- прямую, проходящую через две заданные точки;
- произвольную окружность с центром в заданной точке;
- произвольную окружность с радиусом, равным расстоянию между двумя заданными точками;
- окружность с центром в заданной точке и с радиусом, равным расстоянию между двумя заданными точками.
Требуется с помощью конечного количества этих операций построить другое множество объектов, находящееся в заданном соотношении с исходным множеством.
Решение задачи на построение содержит в себе три существенные части:
- Описание способа построения заданного множества.
- Доказательство того, что множество, построенное описанным способом, действительно находится в заданном соотношении с исходным множеством. Обычно доказательство построения производится как обычное доказательство теоремы, опирающееся на аксиомы и другие доказанные теоремы.
- Анализ описанного способа построения на предмет его применимости к разным вариантам начальных условий, а также на предмет единственности или неединственности решения, получаемого описанным способом.
- Задача Аполлония о построении окружности, касающейся трех заданных окружностей. Если ни одна из заданных окружностей не лежит внутри другой, то эта задача имеет 8 существенно различных решений.
Построение правильных многоугольников[править | править код]
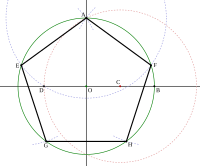 Построение правильного пятиугольника
Построение правильного пятиугольникаАнтичным геометрам были известны способы построения правильных n-угольников для n=2k{\displaystyle n=2^{k}}, n=3⋅2k{\displaystyle n=3\cdot 2^{k}}, n=5⋅2k{\displaystyle n=5\cdot 2^{k}} и n=3⋅5⋅2k{\displaystyle n=3\cdot 5\cdot 2^{k}}.
В 1796 году Гаусс показал возможность построения правильных n-угольников при n=2k⋅p1⋯pm{\displaystyle n=2^{k}\cdot p_{1}\cdots p_{m}}, где pi{\displaystyle p_{i}} — различные простые числа Ферма. В 1836 году Ванцель доказал, что других правильных многоугольников, которые можно построить циркулем и линейкой, не существует.
Неразрешимые задачи[править | править код]
Следующие три задачи на построение были поставлены ещё древними греками:
Лишь в XIX веке было строго доказано, что все эти три задачи неразрешимы при использовании только циркуля и линейки. Доказательство неразрешимости этих задач построения было достигнуто с помощью алгебраических методов, основанными на теории Галуа[1]. В частности, невозможность построения квадратуры круга следует из трансцендентности числа π.
Другая известная и неразрешимая с помощью циркуля и линейки задача — построение треугольника по трём заданным длинам биссектрис[2]. Эта задача остаётся неразрешимой даже при наличии инструмента, выполняющего трисекцию угла, например томагавка.[3]
Допустимые отрезки для построения с помощью циркуля и линейки[править | править код]
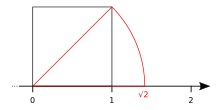 Построение квадратного корня из 2.
Построение квадратного корня из 2. 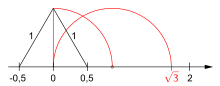 Построение квадратного корня из 3.
Построение квадратного корня из 3. 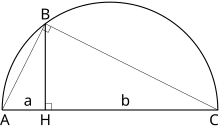
С помощью этих инструментов возможно построение отрезка, который по длине:
- равен сумме длин нескольких отрезков;
- равен разности длин двух отрезков;
- численно равен произведению длин двух отрезков;
- численно равен частному от деления длин двух отрезков;
- численно равен квадратному корню из длины заданного отрезка (следует из возможности построения среднего геометрического двух отрезков, см. иллюстрацию).[4]
Для построения отрезка с длиной численно равной произведению, частному и квадратному корню из длин заданных отрезков необходимо задание на плоскости построения единичного отрезка (то есть отрезка длины 1), иначе задача неразрешима из-за отсутствия масштаба. Извлечение корней из отрезков с иными натуральными степенями, не являющимися степенью числа 2, невозможны с помощью циркуля и линейки. Так, например, невозможно при помощи циркуля и линейки из единичного отрезка построить отрезок длиной 23{\displaystyle {\sqrt[{3}]{2}}}. Из этого факта, в частности, следует неразрешимость задачи об удвоении куба.[5]
С формальной точки зрения, решение любой задачи на построение сводится к графическому решению некоторого алгебраического уравнения, причем коэффициенты этого уравнения связаны с длинами заданных отрезков. Поэтому можно сказать, что задача на построение сводится к отысканию действительных корней некоторого алгебраического уравнения.
Поэтому удобно говорить о построении числа — графического решения уравнения определенного типа.
Исходя из возможных построений отрезков возможны следующие построения:
Иначе говоря, возможно строить лишь отрезки, равные арифметическим выражениям с использованием квадратного корня из исходных чисел (заданных длин отрезков).
Важно отметить, что существенно, что решение должно выражаться при помощи квадратных корней, а не радикалов произвольной степени. Если даже алгебраическое уравнение имеет решение в радикалах, то из этого не следует возможность построения циркулем и линейкой отрезка, равного его решению. Простейшее такое уравнение: x3−2=0,{\displaystyle x^{3}-2=0,} связанное со знаменитой задачей на удвоение куба, сводящаяся к этому кубическому уравнению. Как было сказано выше, решение этого уравнения (23{\displaystyle {\sqrt[{3}]{2}}}) невозможно построить циркулем и линейкой.
Возможность построить правильный 17-угольник следует из выражения для косинуса центрального угла его стороны:
- cos(2π17)=−116+11617+11634−217+{\displaystyle \cos {\left({\frac {2\pi }{17}}\right)}=-{\frac {1}{16}}\;+\;{\frac {1}{16}}{\sqrt {17}}\;+\;{\frac {1}{16}}{\sqrt {34-2{\sqrt {17}}}}\;+\;}
- +1817+317−34−217−234+217,{\displaystyle +{\frac {1}{8}}{\sqrt {17+3{\sqrt {17}}-{\sqrt {34-2{\sqrt {17}}}}-2{\sqrt {34+2{\sqrt {17}}}}}},}
- что, в свою очередь, следует из возможности сведения уравнения вида xFn−1=0,{\displaystyle x^{F_{n}}-1=0,} где Fn{\displaystyle F_{n}} — любое простое число Ферма, с помощью замены переменной к квадратному уравнению.
- Построения с помощью одного циркуля. По теореме Мора — Маскерони с помощью одного циркуля можно построить любую фигуру, которую можно построить циркулем и линейкой. При этом прямая считается построенной, если на ней заданы две точки.
- Построения с помощью одной линейки. Очевидно, что с помощью одной линейки можно проводить только проективно-инвариантные построения. В частности,
- невозможно даже разбить отрезок на две равные части,
- также невозможно найти центр данной окружности.
- Однако,
- при наличии на плоскости заранее проведённой окружности с отмеченным центром с одной линейкой можно провести те же построения, что и циркулем и линейкой (теорема Штейнера — Понселе).
- Если на линейке есть две засечки, то построения с её помощью эквивалентны построениям с помощью циркуля и линейки (важный шаг в доказательстве этого сделал Наполеон).
- Построения с помощью инструментов с ограниченными возможностями. В задачах такого рода инструменты (в противоположность классической постановке задачи) считаются не идеальными, а ограниченными: прямую через две точки с помощью линейки можно провести только при условии, что расстояние между этими точками не превышает некоторой величины; радиус окружностей, проводимых с помощью циркуля, может быть ограничен сверху, снизу или одновременно и сверху, и снизу.
- Построения с помощью плоского оригами см. правила Фудзиты
- Построения с помощью шарнирных механизмов — это построения на плоскости и в пространстве с помощью единичных стержней, связанных на концах шарнирами. Этим способом можно построить любое алгебраическое число[6].
- Программные пакеты динамической геометрии позволяют выполнять виртуальные построения с помощью циркуля и линейки на мониторе компьютера.
- ↑ Кириченко, 2005, с. 1.
- ↑ Кто и когда доказал невозможность построения треугольника по трем биссектрисам?. Дистанционный консультационный пункт по математике МЦНМО.
- ↑ Можно ли построить треугольник по трем биссектрисам, если кроме циркуля и линейки разрешается использовать трисектор. Дистанционный консультационный пункт по математике МЦНМО.
- ↑ Кириченко, 2005, с. 4.
- ↑ Кириченко, 2005, с. 9.
- ↑ Maehara, Hiroshi (1991), «Distances in a rigid unit-distance graph in the plane», Discrete Applied Mathematics Т. 31 (2): 193–200, DOI 10.1016/0166-218X(91)90070-D .
- ↑ Стандарт флага Ирана Архивная копия от 21 июня 2012 на Wayback Machine (перс.)
- Адлер А. Теория геометрических построений / Перевод с немецкого Г. М. Фихтенгольца. — Издание третье. — Л.: Учпедгиз, 1940. — 232 с.
- Александров И. И. Сборник геометрических задач на построение. — Издание восемнадцатое. — М.: Учпедгиз, 1950. — 176 с.
- Аргунов Б. И., Балк М. Б. Геометрические построения на плоскости. Пособие для студентов педагогических институтов. — Издание второе. — М.: Учпедгиз, 1957. — 268 с.
- Воронец А. М. Геометрия циркуля. — М.-Л.: ОНТИ, 1934. — 40 с. — (Популярная библиотека по математике под общей редакцией Л. А. Люстерника).
- Гейлер В. А. Неразрешимые задачи на построение // СОЖ. — 1999. — № 12. — С. 115—118.
- Кириченко В. А. Построения циркулем и линейкой и теория Галуа // Летняя школа «Современная математика». — Дубна, 2005.
- Манин Ю. И. Книга IV. Геометрия // Энциклопедия элементарной математики. — М.: Физматгиз, 1963. — 568 с.
- Петерсен Ю. Методы и теории решения геометрических задач на построение. — М.: Типография Э. Лисснера и Ю. Романа, 1892. — 114 с.
- Прасолов В. В. Три классические задачи на построение. Удвоение куба, трисекция угла, квадратура круга. — М.: Наука, 1992. — 80 с. — (Популярные лекции по математике).
- Геометрические построения // Справочник по математике (для ср. уч. заведений)/ Цыпкин А.Г., под ред. Степанова С.А. — 3-е изд. — М.: Наука, Гл. редакция физ.-мат. литературы, 1983. — С. 200–213. — 480 с.
- Штейнер Я. Геометрические построения, выполняемые с помощью прямой линии и неподвижного круга. — М.: Учпедгиз, 1939. — 80 с.
- Факультативный курс по математике. 7-9 / Сост. И. Л. Никольская. — М.: Просвещение, 1991. — С. 80. — 383 с. — ISBN 5-09-001287-3.
Как построить прямой угол?
Прежде, чем узнать, как построить прямой угол, нужно вспомнить его определение. Прямым называется угол в девяносто градусов, образованный двумя перпендикулярными прямыми. Можно также сказать, что это половина развернутого угла. Существует несколько способов построения прямого угла.
Способы построения прямого угла
Самое простое – построение прямого угла при помощи чертежного угольника. Его прикладывают к бумаге и проводят линии вдоль перпендикулярных сторон: получается прямой угол.Также можно использовать транспортир. К проведенной карандашом линии приложить транспортир, отметить на бумаге угол девяносто градусов. Затем соединить линией (по линейке) эту отметку с линией на бумаге.
- Существует метод построения прямого угла с помощью циркуля и линейки. Сначала нужно циркулем обрисовать окружность и начертить ее диаметр. Затем отметить на окружности произвольную точку и соединить ее с концами диаметра: получится треугольник, вписанный в окружность. Его угол (с вершиной в точке на окружности) будет прямым.
- Второй способ – нарисовать две любые пересекающиеся окружности. Две точки пересечения соединить одной линией, другую – провести через центры окружностей. Два этих отрезка пересекутся под углом 90 градусов.
- Если нет чертежных инструментов, можно воспользоваться любыми прямоугольными предметами. Это может быть лист картона, любая упаковка (от лекарства, пачка от сигарет, коробка конфет и т.д.), книжка, рамка для фото и др.
Построение прямых углов на местности
Вообще, построение прямых углов на местности необходимо в строительстве, при разделе участков земли и т.д. Для этого используются специальные приборы – экер, астролябия, теодолит. Но, вряд ли эти инструменты окажутся, к примеру, на дачном участке. Тогда можно воспользоваться методом, применяемым с давних времен. Понадобятся три колышка и веревки по 3, 4 и 5 метров. Воткнуть в землю колышек, к нему привязать веревки 3 и 4 метра, а к их концам – остальные колья. Последние два колышка соединить 5-метровой веревкой, натянуть получившийся треугольник, и забить эти колья в землю. Угол треугольника с первым колышком будет прямым.
Как видите, существует масса несложных способов построения прямого угла.
Построение с помощью циркуля и линейки. Видеоурок. Геометрия 7 Класс
На этом уроке мы рассмотрим задачи на построение геометрических объектов с помощью циркуля и линейки.
Для решения разных практических задач люди придумали множество инструментов.
Чтобы измерить длину отрезка или нарисовать отрезок заданной длины, мы используем линейку. Для решения аналогичной задачи для углов есть транспортир.
Доказывая теоремы и решая задачи, мы до сих пор не обращали внимания на такие вещи, как: «проведем (построим) медиану треугольника…».
Медиана – отрезок, соединяющий вершину с серединой противоположной стороны. Где вершина, понятно. А где середина противоположной стороны? Если у нас есть под рукой линейка, то решить эту задачу точно не составит труда: измерили длину стороны, разделили на 2, нашли середину. С транспортиром таким же способом несложно построить биссектрису угла.

Рис. 1. С помощью веревки можно нарисовать окружность
В геометрии говорят о задачах на построение с помощью циркуля и линейки. Есть задачи, которые можно решить с этими двумя инструментами, а есть те, которые нельзя. Об этом мы и поговорим на сегодняшнем уроке.
Но прежде попробуем ответить на вопрос: почему именно циркуль и линейка без делений? Почему нельзя было выбрать линейку с делениями, транспортир или какие-то другие инструменты? И зачем вообще нужно уметь решать такие задачи (можем открыть страшную тайну: даже студенты математических факультетов и профессиональные математики не изучают и не решают такие задачи по окончании школы).
Одно соображение мы уже озвучили: все, что можно сделать с циркулем и линейкой (по умолчанию в этом уроке мы будем подразумевать, что имеется в виду линейка без делений), можно сделать и с помощью обычной веревки. И в каких-то ситуациях (например, разметить участок) эти умения могут пригодиться.
Но более важный аргумент – это пример задач, которые решаются с использованием минимального возможного ресурса. В жизни мы часто сталкиваемся с такими задачами: построить двигатель, чтобы за 100 литров бензина проехать максимальное расстояние, или потратить наименьшее возможное время на выполнение домашнего задания, но получить при этом за него не меньше 4, и т. д. Т. е. мы часто решаем задачи на оптимизацию в условиях ограниченного ресурса. В задачах на построение ограничены инструменты, которыми мы можем пользоваться.
Зачем учиться решать задачи на построение?
Некоторым могут показаться неубедительными приведенные аргументы. В необходимости изучения этой темы действительно есть большие сомнения. Но все же приведем еще некоторые соображения, которые могут помочь ответить на сформулированные вопросы.
Математика работает с абсолютно точными моделями (идеальной окружности в жизни не существует, но математика занимается изучением свойств именно такой окружности, чтобы можно
Угол. Прямой и развернутый угол. Чертежный треугольник
Данная тема рассматривалась ранее.
Повторить эту тему можно, перейдя по ссылке
1. Полный угол (см. Рис. 1)
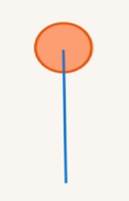
Рис. 1. Полный угол
Стороны угла совпадают.
Меньший угол не виден. Он называется нулевым углом.
Зато второй угол, больший, захватил плоскость полностью. Такой угол называется полным. Вот он имеет для нас важное значение. Поделив его пополам, а потом еще раз пополам, мы получим еще два типа важных углов.
2. Развернутый угол (см. Рис. 2.)
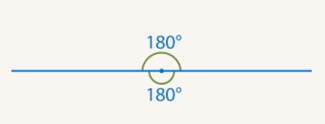
Рис. 2. Развернутый угол
Если стороны угла будут смотреть в разные стороны, составляя прямую, то два полученных угла будут равны друг другу. При этом вместе они составляют полный угол.
То есть угол, образованный такими лучами, является половиной полного угла.
Сам угол похож на то, как если бы ножки циркуля развернули в разные стороны. Угол так и назвали – развернутым.
3. Прямой угол
Поделим уже развернутый угол пополам. Получим два равных угла (см. Рис. 3).
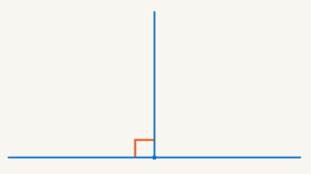
Рис. 3. Прямой угол
Если столб стоит на земле прямо, то мы видим, что углы с двух сторон равны друг другу. Угол так и называется – прямой. Для него вместо дуги договорились использовать специальную отметку, маленький уголок.
1. Чтобы начертить полный угол, нужно из точки провести луч, подразумевая, что это два совпадающих луча.
2. Чтобы начертить развернутый угол, нужно провести прямую и поставить на ней точку. Получим два луча, идущих в разные стороны, то есть развернутый угол.
3. Чтобы начертить прямой угол, легче всего воспользоваться готовым деревянным или металлическим прямым углом, который называется чертежным треугольником, или угольником (см. Рис. 4).

Рис. 4. Чертежный треугольник
Часто уже есть прямая и точка на ней и нужно провести через эту точку вторую прямую под прямым углом к первой.
Совместим угольник одной стороной с имеющейся прямой так, чтобы его вершин
Построение угла, равного данному / Построения циркулем и линейкой / Треугольники / Справочник по геометрии 7-9 класс
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Треугольники
- Построения циркулем и линейкой
- Построение угла, равного данному
Пример:
Отложить от данного луча угол, равный данному.
Дано: луч ОМ, 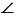 А.
А.
Отложить: от луча ОМ угол, равный 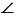 А.
А.
Решение:
Произвольно строим с помощью линейки 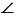 А и луч ОА.
А и луч ОА.
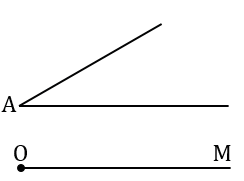
Строим с помощью циркуля окружность произвольного радиуса с центром в вершине 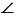 А.
А.
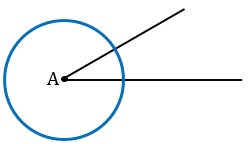
Точки пересечения окружности со сторонами 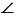 А обозначаем В и С, соединяем их с помощью линейки.
А обозначаем В и С, соединяем их с помощью линейки.
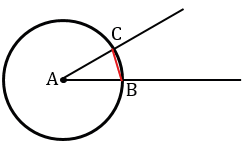
Построим с помощью циркуля окружность того же радиуса, как и окружность с центром в вершине 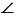 А, от начала луча ОМ точке О.
А, от начала луча ОМ точке О.
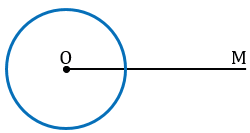
Точку пересечения данной окружности с лучом ОМ обозначим D.
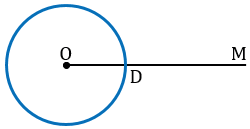
Теперь строим с помощью циркуля окружность радиуса ВС с центром в точке D.

Получаем окружности с центрами в точках О и D пересекаются в двух точках, обозначим одну из этих точек Е.
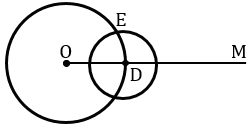
С помощью линейки проведем луч ОЕ.
Докажем, что  МОЕ — искомый угол, т.е.
МОЕ — искомый угол, т.е. 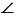 МОЕ =
МОЕ = 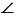 А.
А.
Рассмотрим треугольники АВС и ОDE.
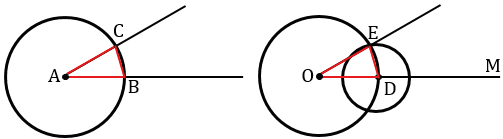
Отрезки АВ и АС — радиусы окружности с центром в точке А, ОD и ОЕ — радиусы окружности с центром в точке О, а по построению эти окружности имеют одинаковые радиусы, следовательно, АВ = ОD, АС = ОЕ. Также по построению радиус DE окружности с центром в точке D равен отрезку ВС, т.е. DE = ВС. Получаем  АВС =
АВС = ODE по 3 признаку равенства треугольников, следовательно,
ODE по 3 признаку равенства треугольников, следовательно, 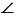 DОЕ =
DОЕ =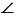 ВАС, т.е. построенный
ВАС, т.е. построенный 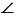 МОЕ равен данному
МОЕ равен данному 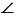 А (т.к. по рисунку видно, что
А (т.к. по рисунку видно, что 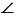 DОЕ совпадает с
DОЕ совпадает с 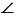 МОЕ, а
МОЕ, а 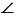 ВАС совпадает с
ВАС совпадает с 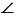 А). Что и требовалось доказать.
А). Что и требовалось доказать.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Построение биссектрисы угла
Построение перпендикулярных прямых
Построение середины отрезка
Среднее пропорциональное
Треугольник
Равенство треугольников
Первый признак равенства треугольников
Перпендикуляр к прямой
Медианы треугольника
Биссектрисы треугольника
Высоты треугольника
Равнобедренный треугольник
Свойства равнобедренного треугольника
Второй признак равенства треугольников
Третий признак равенства треугольников
Окружность
Построения циркулем и линейкой
Треугольники
Правило встречается в следующих упражнениях:
7 класс
Задание 291, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 356, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 585, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 586, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 588, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 871, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 875, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 900, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1144, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1182, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
© budu5.com, 2020
Пользовательское соглашение
Copyright
Построение с помощью циркуля и линейки 📏 описание геометрических фигур, алгоритмы построения отрезков и углов, задачи с решениями
Построение с помощью циркуля и линейки – древнейший способ расчета в евклидовой геометрии. Известен со времен Древней Греции. Данная тема изучается в средних и старших классах на уроках геометрии.
Рассмотрим все случаи построения на конкретных примерах.
Построение отрезка, равного данному
Есть отрезок СD. Задача — начертить равнозначный данному отрезок той же величины.
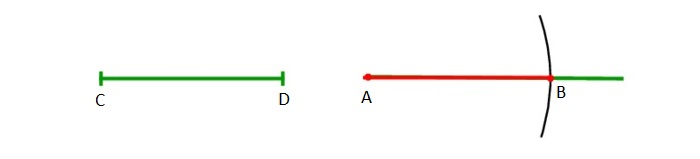
Строится луч, имеющий начало в т. A. Циркуль отмеряет существующий отрезок CD. Циркулем откладывается отрезок, равнозначный первому отрезку, на том же начерченном луче от его начала (A).
Для подобного чертежа ножку с иглой закрепляют в начале луча A, а с помощью части с грифелем проводится дуга до места соприкосновения с лучом. Данную точку можно обозначить т. B.
Отрезок AB будет равнозначен отрезку СD. Задача решена.
Деление отрезка пополам
Имеется отрезок AB.
Сначала следует нарисовать окружность с радиусом больше половины отрезка AB с центром в т. A.
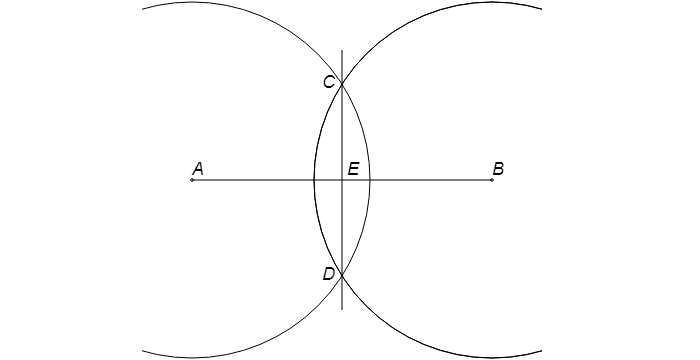
Далее чертится круг с тем же радиусом с серединой в т. B. В местах пересечения окружностей имеем т. C и т. D.
Сквозь эти точки требуется провести прямую линию. Получаем т. E, которая будет серединой отрезка AB.
Построение угла, равного данному
Имеется угол ABC.
Вблизи угла проводится луч ED. Далее чертится окружность с серединой в т. B. В итоге имеем точки M и N.
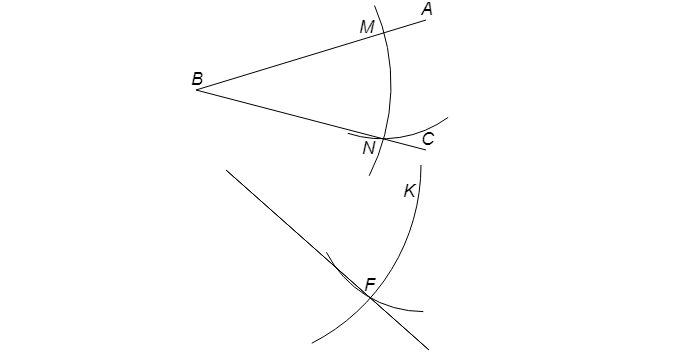
Оставив раствор циркуля прежним, рисуют круг с серединой в т. E. В точке соприкосновения имеем т. K.
Поменяв раствор циркуля на длину расстояния между т. M и т. N, нужно провести окружность с серединой в т. K. В итоге получается т. F. После чертится прямая из т. E через т. F. Образуется угол DEF, который будет равнозначен углу ABC. Задача решена.
Построение перпендикулярных прямых
Пример 1
Точка O находится на прямой a.
Есть прямая и точка, находящаяся на ней. Нанести линию, идущую через существующую точку и находящуюся под прямым углом к имеющейся прямой.
-
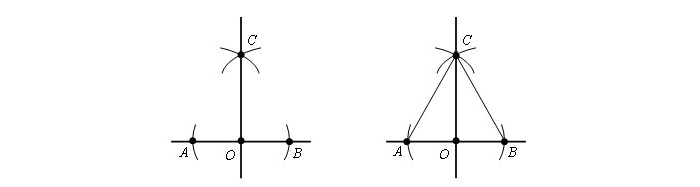
Шаг 1. Чертим круг с рандомным радиусом r с серединой в т. O. Окружность соприкасается с прямой в т. A и т. B.
-
Шаг 2. Из имеющихся точек строится круг с радиусом AB. Точки С и D являются точками соприкосновения окружностей.
Приложив линейку, чертят прямую, сквозь т. O и одну из т. C или т. D, к примеру отрезок OC.
Доказательство, что прямая OC лежит перпендикулярно a.
Намечаются два отрезка — AC и CB. Получившиеся треугольники будут равны, согласно третьему признаку равенства треугольников. Значит, прямая CO перпендикулярна AB.
Пример 2
Точка O находится вне прямой а.
Нарисовать окружность с радиусом r из т. O. Она должна проходить сквозь прямую a. A и B — точки её соприкосновения с прямой.
Оставив прежний радиус, рисуем окружности с серединой в т. A и т. B. Точка O1 — место их соприкосновения.
Рисуем линию, соединяющая т. O и т. O1.
Доказательство выглядит следующим образом.
Две прямые ОО1 и AB пересекаются в т. C. Согласно третьему признаку равенства всех треугольников AOB = BO1A. Из данного вывода следует, что угол OAC = O1AC. Одноименные треугольники также будут равны (согласно первому признаку равенства всех треугольников).
Исходя из этого, выводим, что угол OCA = O1CA, а, учитывая смежность углов, приходим к пониманию, что они прямые. А это означает, что OC – перпендикулярный отрезок, опущенный из т. O на прямую a. Задача решена.
Построение параллельных (непересекающихся) прямых
Имеется прямая и т. А, не лежащая на этой прямой.
Нужно отметить прямую, проходящую через т. A, и параллельную имеющейся прямой.
Берется рандомная точка на имеющейся прямой и именуется B. С помощью циркуля строится окружность радиуса AB с серединой в т. B. В месте пересечения окружности и данной прямой отмечается т. C.
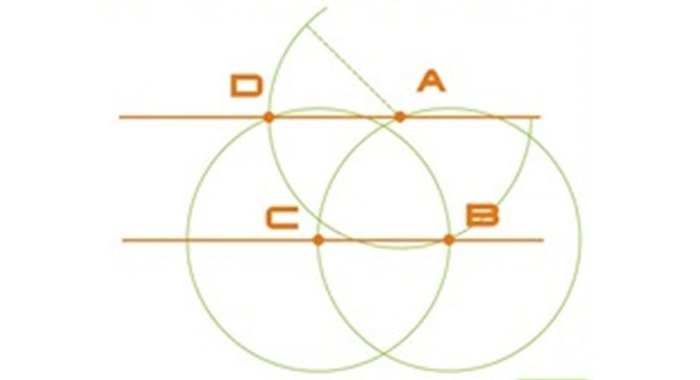
Оставив прежний радиус, рисуется еще одна окружность, теперь уже с центром в т. C. При правильных расчетах дуга должна пройти через т. B.
C тем же радиусом AB строится окружность с серединой в т. A. Точку соприкосновения второй и третьей окружностей назовем D. Третья окружность, учитывая верность расчетов, также пройдет через т. B.
Проводится прямая через т. A и т. D, которая станет параллельной первой. В итоге, получились две параллельные прямые, BC и AD.
Задача решена.
Построение правильного треугольника, вписанного в окружность
Правила построения правильного треугольника, вписанного в окружность:
Отметить отрезок AB, чья длина будет равняться а.
Взять циркуль. Часть с иголкой расположить на т. А, а часть с карандашом на т. B. Прочертить окружность. В итоге, радиус круга будет равнозначен длине отрезка AB.
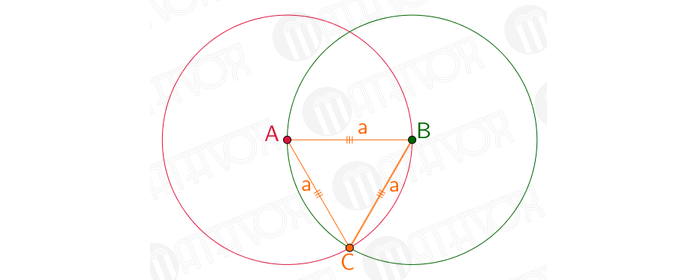
Далее иглу размещают на т. B, а часть с грифелем на т. A. Чертится круг. В итоге, его радиус будет равнозначен длине отрезка AB.
На чертеже окружности пересеклись в двух точках. Далее нужно соединить т. A и т. B и одну из вышеупомянутых точек. В результате получится равносторонний треугольник.
Стороны такого треугольника равнозначны радиусам двух окружностей, которые равны длине а. Задача решена.
Построение правильного четырехугольника вписанного в окружность
Вариант 1
Исходя из данности, что диагонали любого квадрата пересекаются в середине окружности и находятся по отношению к его осям под углом 45 градусов, производят следующие действия. Пользуясь линейкой и уголком с углами 45 градусов (см. рисунок), размечают вершины т. 1 и т. 3.
Сквозь данные точки чертят отрезки, стороны четырехугольника, расположенные по горизонтали. Это т. 4 и т. 1, т. 3 и т. 2. В конце линейкой и уголком по его катету проводятся линии, расположенные по вертикали (высоты), отрезок т.1 — т. 2 и отрезок т. 4 — т. 3.
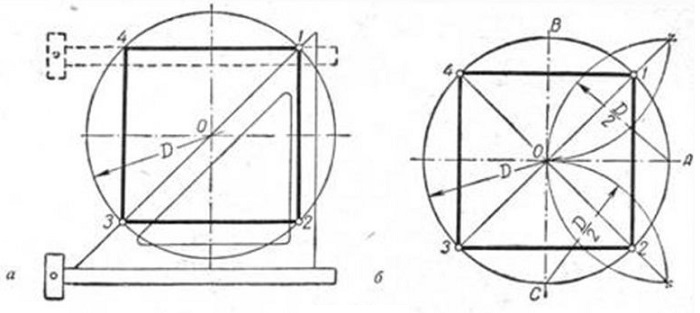
Вариант 2
Так как вершины правильного четырехугольника разделяют наполовину дуги окружностей, между точками диаметра (см. рисунок), то для достижения результата делают следующее: отмечают на точках перпендикулярных диаметров т. A, т. B и т. C и рисуют дуги до их соприкосновения.
После чертят прямые через места соприкосновения дуг, которые выделены на фигуре линиями. Точки соприкосновения с окружностью будут являться вершинами — это т. 1 и т. 3, т. 4 и т. 2. Данные вершины полученного квадрата соединяют друг с другом.
Задача выполнена двумя способами.
Построение вписанного в окружность правильного пятиугольника
Поместить на окружность т. 1, считая ее за вершину пятиугольника. Разделить отрезок AO пополам. Чтобы произвести подобную операцию, из т. A чертят дугу до места соприкосновения с окружностью в т. M и т. B.
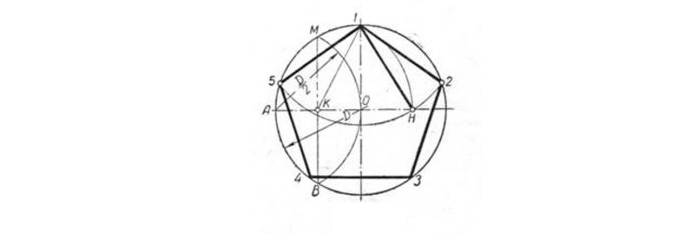
Расположив конкретные точки на прямой, получаем т. K, и после совмещаем с т. 1. Радиусом, длина которого – отрезок А1, сделать изгиб из т. K до места соприкосновения с линией АО в т. H. После совместить т. 1 и т. H, образуя одну из пяти сторон пятиугольника.
Взять циркуль, величина раствора которого будет равна отрезку т.1 — т. H, нарисовать изгиб из т. 1 до соприкосновения с кругом. Так находят вершины 2 и 5. Отметив точки на вершинах 2 и 5, получают вершины 3 и 4. В конце все точки совмещают друг с другом.
Задача выполнена.
Построение правильного шестиугольника, вписанного в окружность
Решение подобной задачи строится на свойствах, где сторона шестиугольника равнозначна радиусу круга.
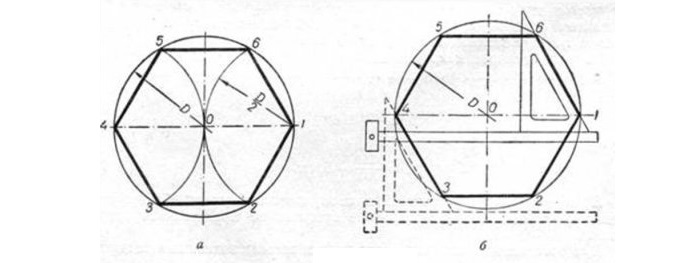
Для расчета разделяют круг на шесть ровных частей и последовательно совмещают все полученные точки (см. рисунок). Задача решена.
