Как определить угол наклона: Определение угла наклона, простые формулы для расчета

Онлайн калькулятор уклонов в процентах и градусах

Скачать, сохранить результат

Выберите способ сохранения

Информация

Сфера строительства развивается с каждым днем, но важность максимальной точности при расчетах тех или иных значений показателей остается прежней. Раньше расчеты требовали знания множества формул, которые не всегда простые. Люди получают высшее образование для того, чтобы иметь возможность работать в строительной отрасли. Сегодня необходимость в заучивании формул и самостоятельно расчете всех показателей исчерпала себя. Был создан онлайн-калькулятор, который рассчитывает любые интересующие Вас показатели. Для расчета необходимо просто ввести исходные данные, которые потребует калькулятор, а после он автоматически выдаст Вам показатель с предельной точностью.

Калькулятор уклонов является одним из таких инструментов. Он позволит произвести расчет уклона и избавит от долгих и крайне важных расчетов. Обычно данный расчет требует при строительстве частных домов, на крышу которого кладется кровля и при кладке необходимо рассчитать уклон кровли в процентах. В этих случаях наш онлайн-калькулятор избавит Вас от лишних трудностей. Также есть возможность рассчитать уклон кровли в процентах, а некоторые случаи могут требовать просчитать уклон кровли в промиллях.

Какие преимущества дает калькулятор уклонов:

Предельная точность выполненных расчетов, которая позволит Вам избежать неудач в процессе строительства.

• Экономия времени, благодаря исключению необходимости самостоятельных расчетов.
• Комфортный интерфейс калькулятора, который также принесет Вам определенное удовольствие от работы и не заставит долго разбираться в его работе.

Для того, чтобы воспользоваться нашим калькулятором, Вам необходимо зайти на сайт и провести следующие действия:

Определить что именно нужно посчитать (превышение через уклон и расстояние, уклон через превышение и расстояние или расстояние через превышение и уклон).

• Выбрать единицу измерения.
• Ввести данные и нажать кнопку «рассчитать».
• Пролистать вниз страницы и Вы увидите точный ответ.

поделиться и оценить

Смотрите также:

Добавить комментарий

минимальный наклон, зависимость, влияние факторов и расчет

Содержание статьи:

Обустройство стропильной системы и укладка кровельного материала являются заключительным этапом строительства жилых и хозяйственных зданий. Данная фаза не менее важна, чем возведение фундамента и стен. От правильности ее планирования зависит герметичность, прочность, устойчивость и функциональность всего сооружения. Не последнее значение в проектировании имеет угол наклона крыши. Этот показатель определяет эстетическую сторону строения и его эксплуатационные характеристики. Чтобы принять грамотное решение, следует изучить существующие разновидности конструкций крыш и нормы, которые применяются при проектировании угла наклона кровли.

Виды крыш и их зависимость от угла наклона

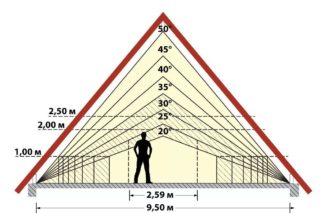
Угол наклона крыши зависит от климата, кровельного покрытия, типа стропильной системы

По форме и крутизне различают такие типы кровель:

• Односкатная. Представляет собой наклонную плоскость без перепадов и изломов. Является простейшей конструкцией в плане сборки, но ограниченной по функциональности. Уклон плоской кровли определяется видом покрытия и ветровой нагрузкой.
• Двускатная. Является классикой и считается наиболее популярной среди частных застройщиков. Состоит из двух поверхностей, соединенных в верхней части коньковой балкой. Между скатами обустраиваются вертикальные треугольные стены — фронтоны.
• Шатровая. Состоит из четырех равнобедренных треугольников, образующих пирамиду правильной формы. Обеспечивает идеально прочную монолитную конструкцию. Уклон кровли варьируется в пределах 15-60 градусов, в зависимости от климатических условий и накрывочного материала.
• Вальмовая. Четырехскатная схема, образованная трапециевидными и треугольными поверхностями. Отличаются сложностью проектирования каркаса и высокими эстетическими характеристиками. Угол ската крыши крутой, что обусловлено особенностями проекта.
• Сводчатая. Имеет сложные криволинейные скаты с плавными и резкими переходами. В строительстве используется редко, так как для создания опорной системе применяется несколько видов материалов — кирпич, железобетон и древесина. Уклон крыши делается большим, так как используется гибкое покрытие – мягкая черепица или наплавляемая кровля.
• Многощипцовая. Наиболее сложная в проектировании и исполнении, но самая эффектная конфигурация. Состоит из совокупности острых фигур, в сборе напоминающая купол замка. Угол крыши максимальный среди аналогов и начинается от 50 градусов.

Градус наклона ската напрямую зависит от дизайна кровли. Ее конфигурация определяет выбор отделочного материала.

Влияние различных факторов на выбор угла наклона

Японский стиль крыши подразумевает особый подход к расчету угла наклона и конфигурации элементов

В большинстве случаев сначала выбирается наиболее эффектная и броская конфигурация кровли с оценкой возможности практического применения чердачного пространства. После этого методом исключения проводится выбор оптимальной крутизны с учетом анализа влияния различных объективных и субъективных факторов.

• Общепринятые правила строительства. Необходимо выбирать уклон крыши по нормам, установленным ГОСТ и СНИП. В противном случае здание не будет введено в эксплуатацию и его придется переделывать.
• Национальные традиции. В каждой местности принято следовать той или иной архитектуре, определяющей местный этнос.
• Сила и направление господствующих ветров. Чем больше интенсивность движения воздушных масс, тем меньше должна быть парусность строения.
• Уровень атмосферных осадков. Это относится к снегу, который в большом количестве может продавить кровельное покрытие и сломать стропила.
• Выбор финишного покрытия. От него зависит диапазон уклона, игнорирование которого приводит к аварийным ситуациям.

Для каждого материала установлен максимальный и минимальный уклон, который рассчитывается с учетом множества сопутствующих данных.

Как произвести расчет

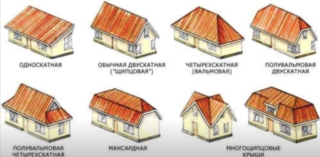
Типы скатных крыш, угол наклона более 30 градусов

Уклон кровли рассчитывается индивидуально для каждого жилья. Изначально нужно определиться с функциональностью чердачного пространства — нужно оно для ведения хозяйства или нет.

Исходя из этого параметра выделяют такие виды кровель:

• Плоские (неэксплуатируемые). Представляют собой сооружения, где между крышей и плитой перекрытия остается минимум пространства, где передвижение людей затруднено или невозможно. Строить такие конструкции выгодно, так как не требуется сложных расчетов, расход материалов минимален. Разуклонка кровли плоской составляет от 3 до 15 градусов в зависимости от материала облицовки и внешних факторов.
• Скатные (эксплуатируемые). Делаются с углом от 30 градусов и больше. Благодаря такому решению образуется просторный чердак, в котором можно обустроить хозяйственные и даже жилые помещения.

Чтобы правильно высчитать оптимальный угол уклона, следует воспользоваться справочной информацией, изложенной в СНиПе II-26-76. Документ содержит таблицы, в которых есть данные относительно региональных коэффициентов: снеговые нагрузки, ветровые показатели, рекомендуемые диапазоны углов скатов для финишной отделки. Считать показатели рекомендуют в проценты, но при желании их можно перевести в градусы, воспользовавшись прилагаемой к нормам таблицей.

Влияние наклона крыши на выбор кровельного материала

Планируемое покрытие для крыши также влияет на угол наклона

Чтобы грамотно рассчитать чертеж кровли, необходимо знать и правильно применять на практике установленные для каждого укрывочного материала нормы:

• твердая черепица из металла, керамики и цемента — 6-30;
• битумная плитка — 12-45;
• шифер, профлист — 7-40;
• фальцевое покрытие из металла — 15-60;
• рубероид и его аналоги — 20-30.

Рекомендации даны в процентах. Цифры прописаны с учетом таких факторов, как способность противостоять ветровым и снеговым нагрузкам, эффективный отвод воды. Кроме этого, необходимо брать в расчет степень герметичности кровли, которая собирается из отдельных фрагментов. Если стыки не заделаны мастикой, уклон нужно увеличивать. Измерить его можно электронным прибором, транспортиром или по соотношению сторон.

Минимальная величина уклона кровли

В снежных регионах угол наклона крыши должен быть не менее 30 градусов

Данные показатели указываются в инструкциях по монтажу ко всем представленным в продаже кровельным материалам.

Определяются они следующими факторами:

• Защита от протекания. Профнастил, шифер и жесткая плитка укладываются в накладку и при уклоне меньше 20 градусов в стыки может проникать вода.
• Снеговая нагрузка. Если он не будет сходить самостоятельно, возникает риск деформации, поломки или разрыва кровельного покрытия, разрушения опорной системы. Рекомендуемый угол — 30 градусов.
• Устойчивость материала на основе. Если к шиферу, профлисту и фальцевым конструкциям это не относится (они прибиваются или прикручиваются), то по отношению к полосам и плитке нужно применять определенные нормативы. Со слишком крутого или пологого ската плитки может сорвать, а наплавляемые покрытия могут сползти.

Чем угол кровли круче, тем крыша выше. Это приводит к большому расходу стройматериалов и возрастанию риска опрокидывания конструкции сильным порывом ветра. Однако и пологие скаты не являются средством экономии. Их нужно делать с мощной стропильной системой, чтобы гарантированно противостоять вертикальной снеговой и горизонтальной ветровой нагрузке.

Климатические факторы

Не рекомендуется строить плоские крыши в регионах с большим количеством осадков

Климатические условия являются важнейшим фактором, который влияет на выбор конструкции крыши и особенно на уклон ее скатов.

Когда масса осадков после сильных снегопадов задерживается на кровле, она впитывает из воздуха влагу, а затем примерзает. Многотонная толща способна сокрушить самые надежные и проверенные несущие конструкции и покрытия. Исходя из этого, нужно соблюдать оптимальный угол крыши для схода снега, который рекомендует производитель. На данный показатель влияет не только угол ската, но и гладкость и состав финишного покрытия.

Не менее важно учитывать ветровую нагрузку. Ураганы не являются редкостью в России и чаще всего они разрушают именно крыши. Потоки воздушных масс валят конструкции или отрывают их от основания. Чтобы этого не допустить, необходимо тщательно посчитать соотношение свесов, крутизны и парусности кровли. Специалисты утверждают, что оптимальным является уклон крыши в пределах 30-45 градусов. Сооружения такого типа обладают пропорциями, которые обеспечивают быстрый сход снега, ливневых вод и в тоже время выдерживают порывы ветра даже экстремальной силы.

Как самостоятельно рассчитывать оптимальный угол наклона крыши

При создании кровли уклон является одним из важнейших параметров, который учитывается в расчетах. Зависит он от материала для кровли, а также местного климата.

Угол наклона крыши является важнейшим параметром при возведении стропильной системы и расчете расхода кровельных материалов частного дома. Проектирование крыши – мероприятие весьма ответственное, которое следует доверить исключительно профессионалам, имеющим разрешение на проведение подобных работ.

Угол наклона крыши

• На что влияет уклон крыши
• В чем измеряется угол наклона крыши
• Правила расчета угла наклона кровли
• Определяем минимальный угол ската крыши в зависимости от кровельного материала
• Снеговые и ветровые нагрузки
• Примеры расчета

Однако в некоторых случаях, все предварительные расчеты можно сделать и самостоятельно, хотя бы для того, чтобы иметь представление о предполагаемом количестве материала и возможности реализации своих архитектурных идей. Из этой публикации вы узнаете, от чего зависит и как своими силами рассчитать угол наклона крыши, не прибегая к услугам дорогостоящих специалистов.

На что влияет уклон крыши

При самостоятельном возведении каркаса крыши большинство застройщиков руководствуется ее дизайном и назначением подкровельного пространства, что в корне неверно. На каркас крутых крыш практически не воздействует снеговая нагрузка, а это значит, что чисто теоретически можно сэкономить на сечении и шаге стропил. Однако ветер, оказывает наибольшее воздействие именно на кровли с крутыми скатами из-за их большой парусности, что уже на практике требует создания прочной стропильной системы.

Все это совершенно не значит, что пологие крыши лучше. На кровлях с малым уклоном снег будет задерживаться дольше, что создает внушительную нагрузку на стропильную систему. К тому же, угол ската крыши влияет на габариты чердачного помещения. Чем круче крыша – тем больше возможности у застройщика для обустройства жилой мансарды. Тем не менее не следует забывать о высокой стоимости конструкций с крутыми скатами, особенно в сравнении с пологими крышами. Сохранить объем чердачного пространства, не увеличивая высоту конька, поможет создание ломаной крыши.

Помимо снеговой и ветровой нагрузки на каркас оказывает влияние и вес кровельного пирога совместно с собственной массой стропильной системы. Если в кровле используются теплоизоляционные материалы, то и их вес учитывается при определении оптимального угла крыши.

В чем измеряется угол наклона крыши

Прежде всего, следует внести ясность в само понятие угол наклона. Данная величина – это угол, который образуется при пересечении горизонтальной плоскости (заложение) с плоскостью кровли. «Заложение» – это не что иное, как проекция ската крыши в горизонтальной плоскости.  

В справочной литературе и специализированных таблицах в качестве единицы измерения угла наклона крыши используются проценты. Уклон кровли в процентах показывает отношение высоты подъема кровли (Н) к заложению (L).

В двускатных крышах (L) – это величина, равная длине половины пролета. L в односкатных крышах равняется длине пролета.

Правила расчета угла наклона кровли

Допустим, L = 3 м, а Н = 1 м. В таком случае отношение будет выглядеть, как Н к L или 1:3. Это простейший пример, показывающий большие неудобства в определении угла уклона таким способом.

Для простоты вычислений применяется специальная формула расчета угла наклона крыши, которая выглядит следующим образом.

I = H/L где:

• I – тангенс уклона ската;
• Н – высота подъема кровли;
• L – значение заложения.

Используем данные из примера выше. L = 3 м и Н = 1 м. Тогда, формула расчета выглядит, как I = 1/3 = 0,33. Теперь, для перевода значения тангенса острого угла в проценты необходимо полученное значение умножить на 100. Исходя из этого, получаем: 0,33 х 100 = 33%

Как определить угол наклона крыши в градусах? Перевести проценты в градусы можно двумя простыми способами:

• воспользоваться онлайн-конвертором;
• воспользоваться таблицами, опубликованными в специализированной справочной литературе.

Первый способ весьма прост, но требует подключения к интернету. В сети представлено огромное количество ресурсов, предоставляющих возможность воспользоваться онлайн-конвертором.

Таблицы уклона крыши в градусах и процентах найти значительно сложнее, однако они проще в применении. Публикуем таблицу соотношения проценты-градусы.

Определяем минимальный угол ската крыши в зависимости от кровельного материала

Исходя из крутизны скатов, все крыши условно делятся на четыре типа:

• Высокие, с уклоном от 45 до 60°.
• Скатные, с углом наклона кровли от 30 до 45°.
• Пологие. Угол наклона скатов в таких конструкциях варьируется от 10 до 30°.
• Плоские с уклоном до 10°.

Подходя к возведению крыши, застройщик планирует использование определенного кровельного материала. Следует учитывать, что далеко не каждый материал может быть использован на крышах с различным уклоном.

Далее рассмотрим зависимость между наиболее распространенными кровельными материалами и минимально допустимым углом ската крыши:

1. Асбоцементный шифер — 9° или 16%. Соотношение высоты подъема кровли к заложению 1:6.
2. Ондулин — 5°. Соотношение сторон 1:11.
3. Минимальный угол наклона односкатной крыши из металлочерепицы составляет 14°.
4. Керамическая черепица — 11°. Соотношение 1:6.
5. Цементно-песчаная черепица — 34° или 67%. Соотношение высоты кровли к заложению 1:1,5.
6. Битумная черепица — 11°. Соотношение сторон 1:5.
7. Профнастил — 12° При меньшем уклоне необходимо провести обработку стыков герметизирующим средством.
8. Оцинковка и стальные листы требуют минимального уклона 17°.
9. Рулонные битумные материалы — 3°.
10. Наплавляемая кровля может быть использована в качестве покрытия крыши с уклоном 15%.

В проектировании крыш существует понятие – максимальный угол наклона скатов. Данное значение является критическим для использования конкретного материала. На рисунке ниже показаны минимальные и максимальные значения угла наклона крыши для некоторых распространенных кровельных материалов. Кроме этого, в последней колонке собраны данные о том, какой уклон ската чаще всего используется для данных материалов отечественными застройщиками.

Как видно из приведенной таблицы, между минимальным и максимальным углом наклона крыши весьма солидный разрыв.

Выбирая уклон из диапазона допустимых значений, следует руководствоваться исключительно эстетическими соображениями и расходом материала.

Снеговые и ветровые нагрузки

При проектировании кровли всегда учитываются снеговые и ветровые нагрузки на стропильную систему. Чем круче скаты, тем меньше снега на них задержится.

Для правильного вычисления необходимой прочности конструкции вводится поправочный коэффициент:

1. Для крыш с уклоном менее 25° применяется коэффициент равный 1.
2. Стропильные конструкции со скатами от 25 до 60° требуют применения коэффициента 0,7.
3. Кровли, выполненные с углом наклона скатов более 60°, не требуют применения коэффициента, так как снег на них практически не задерживается.

Для простоты вычислений используют карты, в которых отмечены средние значения снеговой нагрузки по регионам РФ.

Примеры расчета

Правила проведения расчетов просты: находим свой регион, определяем снеговую нагрузку, выделенную своим цветом, принимаем в расчет первое значение, умножаем на поправочный коэффициент исходя из предполагаемого угла уклона крыши. В качестве наглядного примера рассчитаем снеговую нагрузку для крыши дома в Норильске углом наклона скатов 35°. Итак, 560 кг/м2 умножаем на коэффициент 0,7. Получаем снеговую нагрузку для данного региона и конкретной конструкции кровли 392 кг/м2.

Для определения ветровых нагрузок также используются карты, в которых отмечены расчетные значения ветровых нагрузок по регионам.

Кроме этого, в расчетах следует учитывать:

1. Розу ветров, а конкретно – расположение дома на местности и относительно других строений.
2. Высоту постройки.

По типу расположения дома на местности, все строения можно разделить на три группы:

1. А – постройки, расположенные не открытой местности.
2. Б – Строения, расположенные в населенных пунктах с ветровой преградой не выше 10 м.
3. В – здания, находящиеся в населенных пунктах с ветровой преградой от 25 м.

В зависимости от зоны размещения и высоты строения при проектировании крыши вводятся поправочные коэффициенты, учитывающие ветровую нагрузку. Все факторы, влияющие на ветровую нагрузку, сведены в таблицу, по которой легко сделать расчет.

Например: для одноэтажного дома в Норильске ветровая нагрузка составит: 84 кг/м2 умноженная на коэффициент 0,5, соответствующий зоне «В», что составляет 42 кг/м2.

Помимо этого, учитываются аэродинамические нагрузки, воздействующие на стропильную систему и кровельный материал. В зависимости от направления ветра, нагрузку условно делят на зоны, которые предполагают различные поправочные коэффициенты.

Для обеспечения запаса прочности рекомендуется брать значения из наиболее нагруженных зон G и H. опубликовано econet.ru  

Подписывайтесь на наш канал Яндекс Дзен!

Если у вас возникли вопросы по этой теме, задайте их специалистам и читателям нашего проекта здесь.

P.S. И помните, всего лишь изменяя свое потребление — мы вместе изменяем мир! © econet

Измерение углов наклона — Студопедия

Весьма важной характеристикой вертикального круга, а также параметром, определяющим работу теодолита, является место нуля (МО) вертикального круга. Поясним этот параметр на схеме, представленной на рис. 49.

Предположим, что при положении «круг лево» отсчет на точку местности по вертикальному кругу составил ВК(КЛ). Предположим также, что ноль вертикального круга смещен от положения горизонтальной плоскости на величину МО. При принятой на рисунке оцифровке и ее знаках то же самое можно проследить и при положении «круг право». Разность отсчетов даст значение угла наклона

ν = ВК(КЛ) – МО ; ν = МО — ВК(КП) (80)

С учетом формул (80) можно записать, что

МО = 0,5[ВК(КЛ) + ВК(КП)](81)

Последовательность измерения угла наклона (при установленном в рабочее положение теодолите).

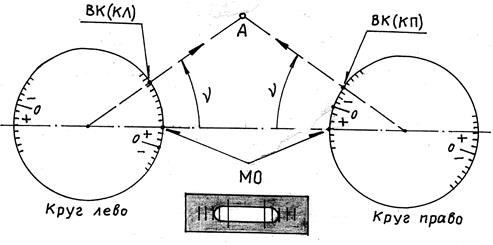
Рис. 49. Измерение угла наклона

1. Выполнить наведение на т. В или С при КЛ, переместив изображение точки наводящими винтами колонки и зрительной трубы на горизонтальную нить сетки нитей вблизи от центрального перекрестия (либо точно в центр сетки нитей). Взять отсчет по шкале вертикального круга (КЛ: точка В — +1º36,5′; точка С — — 3º18,0′) – см. табл. 6.

2. Поменять круг (на КП) и выполнить действия по п. 1. Отсчеты также записать в журнал.

Вычисления заключаются в определении места нуля (МО) вертикального круга по формуле (81).

Таким образом,

МО_В = 0,5 (КЛ_В + КП_В) = 0,5 (+1º36,5′ – 1º38,0′) = — 0,75′ = — 45″ ;

МО_С = 0,5 (КЛ_С + КП_С) = 0,5 (- 3º20,0′ + 3º18,0′) = — 1,0′ = — 60″.

Допускаются расхождения в значениях места нуля не более двойной точности отсчета по вертикальному кругу. В этом случае определяют значения углов наклона без усреднения величины МО по формулам (80).

В примере:

ν _В = +1º36,5′ – (-0,75′) = +1º37,25′ = +1º37’15»;

ν_С = — 3º20,0′ – (-1,0′) = — 3º19,0′ = — 3º19’00».

Обычно значения углов наклона вычисляют только при КЛ (при КП – контрольное вычисление) и записывают в соответствующей строке журнала.

Измерение дальномерных расстояний

При измерении дальномерных расстояний удобно использовать нивелирную рейку с сантиметровыми делениями. В этом случае число сантиметров, например, 43,6 см, между дальномерными нитями сетки нитей будет соответствовать числу метров 43,6 м в дальномерном расстоянии.

При измерении дальномерного расстояния можно число сантиметров между дальномерными нитями определять как разность отсчетов по соответствующим дальномерным нитям. Например, по верхней дальномерной нити отсчет 194,7 см, по нижней дальномерной нити – 151,1 см. Тогда разность (194,7 – 151,1) = 43,6 см и определит искомое дальномерное расстояние в метрах (43,6 м).

Часто, при выполнении тахеометрической съемки, дальномерное расстояние определяют непосредственным счетом сантиметров между дальномерными нитями. Для этого удобно, например, верхнюю дальномерную нить переместить на ближайший целый сантиметровый отсчет, а в некоторых случаях – и на ближайший целый пятисантиметровый отсчет. После этого остается просто отсчитать число искомых сантиметров.

12.1.4. Выполнение 1-й поверки

При производстве 1-й поверки теодолитов устанавливают выполнение следующего условия: «Ось цилиндрического уровня при алидаде горизонтального круга должна быть перпендикулярна к оси вращения теодолита».

Указанное условие проверяют в начале каждого рабочего дня, а также при необходимости и в течение рабочего дня. Перед поверкой теодолит необходимо установить в рабочее положение.

1. Установить ось цилиндрического уровня при алидаде горизонтального круга по направлению на два любых подъемных винта подставки (рис. 50). Вращением этих винтов в противоположные стороны привести пузырек уровня точно на середину.

2. Повернуть колонку на 180^о (это можно выполнить «на глаз» по симметрии частей колонки, либо по отсчетам шкалы горизонтального круга).

Если пузырек уровня отклонился не более чем на два деления ампулы, то условие считают выполненным. В этом случае поверку следует проконтролировать по двум другим подъемным винтам подставки.

3. Если пузырек уровня отклонился более чем на два деления, то половину этого отклонения следует исправить подъемными винтами подставки, вращая их одновременно в противоположные стороны, а другую половину – юстировочными винтами уровня, перемещая его хвостовик вверх или вниз, в зависимости от положения пузырька.

После выполнения юстировки поверку повторяют на других подъемных винтах.

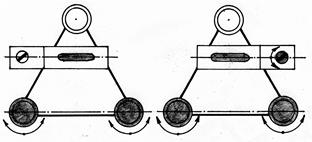Рис. 50. Первая поверка теодолита

Юстировочные винты уровня находятся на одном из его кон-цов. Ими зажат хвостовик уров-ня. Кроме того, многие уровни снабжены и боковыми юстиро-вочными винтами. При выпол-нении юстировки необходимо слегка ослабить боковые юсти-

ровочные винты, а затем отпустить один из юстировочных винтов и подкрутить второй. Этим обеспечивается жесткое положение хвостовика после выполнения каждого шага юстировки. После выполнения поверки и юстировки боковые винты уровня следует снова зажать.

12.2.Нивелир

12.2.1.Назначение основных деталей и узлов нивелира

Нивелир с цилиндрическим уровнем при зрительной трубе (рис. 51) состоит, из подставки 3 с тремя подъемными винтами 4, с помощью которых совместно с круглым уровнем 5 нивелир устанавливают в рабочее положение, наводящего и зажимного устройств, элевационного винта 8, при вращении которого зрительная труба 1 может в небольших пределах поворачиваться в вертикальной плоскости в шарнире 6.

Зрительная труба 1 и цилиндрический уровень 2 жестко скреплены друг с другом. При юстировке положения оси Б-Б уровня эта ось может на небольшие углы поворачиваться относительно оси зрительной трубы в шарнире 7 при вращении в ту или другую сторону юстировочного винта 9, расположенного в хвостовике уровня.

Фокусирование изображения предмета производится кремальерой 11, при вращении которой перемещается отрицательный компонент объектива зрительной трубы (фокусирующая линза или призма). Четкое изображение сетки нитей получают вращением окулярного колена 10.

В поле зрения трубы нивелира выведены специальной оптической системой противоположные концы пузырька цилиндрического уровня.

Нивелиры с компенсаторами не имеют цилиндрического уровня при зрительной трубе, а содержат только установочный (круглый или цилиндрический) уровень, находящийся на корпусе прибора. Приведение

3Н-3КЛ (УОМЗ) 3Н-5Л (УОМЗ)

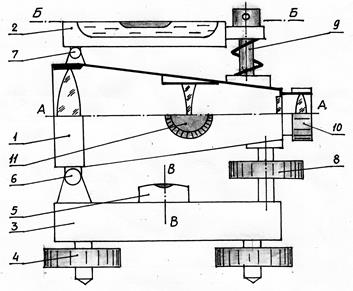Рис. 51. Устройство нивелира

визирной оси нивелира в рабочее положение производится автоматически при приведении в рабочее положение установочного уровня.

12.2.2.Нивелирные рейки

В комплект нивелира входят две нивелирные рейки, представляющие собой бруски или жесткие металлические профилированные полосы с нанесенными на них делениями (обычно сантиметровыми или пятимиллиметровыми). Для точного и технического нивелирования используют деревянные рейки РН-3 и РН-10 с сантиметровыми делениями, нанесенными с двух сторон, каждая из которых окрашена в свой цвет (черная и красная шкалы). Буква С в обозначении рейки говорит о том, что рейка складная. Для точного нивелирования используют не складные, а цельные (с односторонней или двухсторонней шкалами). Высокоточное нивелирование выполняют только с использованием специальных реек типа РН-05 с инварной полосой, на которую нанесены две смещенные шкалы с делениями 5 мм. Инварная полоса имеет устройство для натяжения силой 20 кг. Длина любого интервала шкал такой рейки нанесена с погрешностью не более 0,05 мм. Рейка снабжена круглым уровнем с ценой деления 10′, служащим для установки рейки в вертикальное положение.

Концы реек окованы металлическими пластинами, чем обеспечивается защита пятки реек от повреждений и сохранность начального отсчета.

На черной стороне рейки, используемой для технического или точного нивелирования, нулевой отсчет совпадает с ее пяткой. Наименьшее деление другой шкалы всегда больше наибольшего деления черной шкалы. Тем самым невозможно перепутать при работе черный и красный отсчеты. Например, для реек длиной 3 м наименьший красный отсчет равен 4787 мм (4,787 м). Красные шкалы двух комплектных реек смещены друг относительно друга на 100 мм, например 4787 и 4687. Это позволяет контролировать работу наблюдателя на станции.

12.2.3.Установка нивелира в рабочее положение

Установка нивелира в рабочее положение заключается в установке для наблюдений зрительной трубы и горизонтировании прибора.

Так же, как и для зрительных труб теодолита, установка для наблюдения зрительных труб нивелиров заключается в получении четкого изображения сетки нитей и изображения концов цилиндрического уровня, которое проецируется оптической системой в левую часть поля зрения (у нивелиров с цилиндрическим уровнем при зрительной трубе).

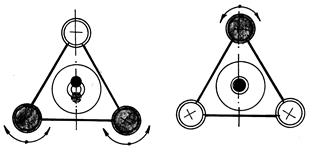Рис. 52. Установка нивелира в рабочее положение

Горизонтирование выполняется приведением пузырька установоч-ного уровня в центр ампулы. Если установочный уровень цилиндричес-кий, то последовательность горизон-тирования такая же, как и при гори-зонтировании теодолита. Если уста-новочный уровень круглый, то для установки нивелира в рабочее положение вращают дваподъем-ных винта в противоположные сто-

роны (рис. 52), выводят пузырек уровня по направлению на третий винт подставки. После этого третьим подъемным винтом приводят пузырек на середину ампулы. Затем установку следует повторить на другом подъемном винте.

Горизонтирование нивелиров, имеющих компенсатор наклона, выполняют аналогично. Высокоточные нивелиры с компенсаторами и нивелиры повышенной точности могут иметь и цилиндрический установочный уровень.

12.2.4.Принцип определения превышения между двумя точками

Превышение на станции геометрического нивелирования определяется как разность отсчетов, полученных по рейкам, установленным в определяемых точках (рис. 53).

Рассмотрим последовательность определения превышения на станции (пример обработки результатов нивелирования приведен в табл. 7).

1. Установить нивелир в рабочее положение.

2. Выполнить наведение зрительной трубы на заднюю точку – рейку А. Для этого получить ее четкое изображение и наводящим винтом переместить это изображение в положение, указанное на рис. 53, справа или слева от вертикальной нити сетки нитей, либо непосредственно по центру.

3. Элевационным винтом привести пузырек цилиндрического уровня на середину. При этом изображения концов пузырька должны совместиться.

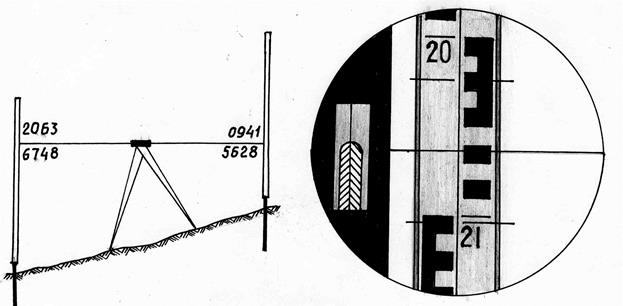
Рис. 53. Измерение превышений нивелиром

4. Взять отсчеты по черной (2063) и красной (6748) сторонам рейки А.

Отсчет по рейке формируется от младшего к старшему, независимо от того, видим мы перевернутое или прямое изображение. На рейках с сантиметровыми делениями подписаны дециметровые штрихи: 06, 13, 57 и т.п., значение которых занимают первые две позиции отсчета. Между дециметровыми штрихами выполнена шашечная разбивка через каждый сантиметр, в связи с чем третьей позиции отсчета соответствует полное число сантиметров между дециметровой оцифровкой и горизонтальной нитью сетки. Четвертая позиция в отсчете – это число миллиметров от последнего полного сантиметрового штриха до горизонтальной нити. Число миллиметров определяют «на глаз». На рис. 53 отсчет равен 2063.

5. Ослабить зажимной винт наводящего устройства и выполнить визирование на рейку В (передняя точка).

6. Элевационным винтом привести пузырек цилиндрического уровня на середину и взять черный (0941) и красный (5628) отсчеты.

На каждой станции контролируют разности красного и черного отсчетов, взятых по соответствующей рейке (контролируют ноль красной пятки). Эти разности не должны отличаться для одной и той же рейки на установленную величину. Для технического нивелирования, например, допускаются в работе колебания значений красной пятки рейки до 5 мм.

6748 – 2063 = 4685; 5628 – 0941 = 4687.

Если указанные разности в пределах допуска, то вычисляют отдельно по черной и красной сторонам реек превышение передней точки В над задней А по формуле

h = Задний отсчет – Передний отсчет (82)

В примере

h_ЧЕРН = 2063 – 0941 = + 1122 (мм),

h_КРАСН = 6748 – 5628 = + 1120 (мм).

Разность полученных превышений не должна превышать установленной величины. Для технического нивелирования допускается разность значений черного и красного превышений на станции не более 5 мм.

Если разность полученных превышений в пределах допуска, то вычисляют среднее превышение

h_СР = 0,5 (h_ЧЕРН + h_КРАСН ) (83)

В примере h_СР = 0,5 [ (+ 1122 ) + ( + 1120 ) ] = + 1121 (мм).

В полевом журнале геометрического нивелирования записи отсчетов и превышений должны иметь четыре позиции. Например, превышение (– 76 мм) должно быть записано как (– 0076). Кроме того, у превышений обязательно указывают знак «плюс» или «минус».

Таблица 7

Определение превышений с помощью нивелира

№ станции	№№ точек	Отсчеты	Превышения
задний	передний	черное красное	среднее
	А			+ 1122	+ 1121
	В			+ 1120
	В			— 0609	— 0610
	С			— 0611

В примере (табл. 7) рассмотрена обработка результатов нивелирования и на следующей по ходу станции: превышение т. С относительно т. В.

12.3.Приборы для линейных измерений

Приборы, используемые для линейных измерений, условно делят на три группы: механические, оптические и физико-оптические. Механические приборы используются для непосредственного измерения расстояний. К ним относятся землемерные ленты, рулетки, тросы, длиномеры, инварные проволоки и др.

Землемерные ленты изготавливают длиной 20 м, 24 м и 50 м. Обозначают землемерные ленты буквами ЛЗ (лента землемерная) и ЛЗШ (лента землемерная штриховая). Изготавливают их из стальной полосы, которая наматывается на барабан. На обоих концах ленты имеются рукоятки, предназначенные для выравнивания полосы на поверхности земли и обеспечения необходимого натяжения при измерениях силой 10 кг.

Рулетки измерительные металлические выпускают нескольких типов: РС – самосвертывающаяся; РЖ – желобчатая; РЗ – в закрытом корпусе; РК – на крестовине; РВ – на вилке; РЛ – с грузом. У рулеток типа А начало шкалы сдвинуто от торца ленты, а у рулеток типа В начало шкалы совпадает с торцом ленты. По точности тип А – 1 и 2 класса, остальные – практически все класса 3 (табл. 8).

Таблица 8

Длина рабочей части ленты, м	Допустимые отклонения действительной длины от номинальной, ±мм
1 класс	2 класс	3 класс
	-	1,0	2,0
	0,5	1,0	2,5
	1,0	2,0	4,0
	-	3,0	5,0
	2,0	5,0	7,0
	-	7,5	10,0
	-	10,0	14,0
Отдельные дециметровые деления и метровые интервалы	0,2	0,3	0,4
Отдельные сантиметровые деления	0,1	0,2	0,3
Отдельные миллиметровые деления	0,05	0,1	0,2

Из оптических дальномеров наибольшее распространение получили нитяный дальномер и дальномеры с переменной базой и переменным параллактическим углом.

К физическим дальномерам относятся радио- и светодальномеры. Существуют отдельные конструкции светодальномеров, которые используются только для измерения расстояний (СМ-5, «Блеск» и др.), а также светодальномеры, конструктивно объединенные с электронным (кодовым) теодолитом. Такая конструкция называется электронным тахеометром.

Далее рассмотрим подробно принцип определения расстояний с помощью нитяного дальномера. Измерение расстояний с помощью мерных лент или рулеток будет рассмотрено далее, при описании выполнения геодезических работ на местности.

Нитяный дальномер имеется практически во всех геодезических приборах (теодолитах, нивелирах). Сетка нитей зрительной трубы содержит две дальномерные нити, проекция которых через зрительную трубу в пространство предмета образует параллактический угол

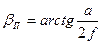, (84)

где а – расстояние между дальномерными нитями на сетке нитей; f – фокусное расстояние объектива зрительной трубы.

При определении расстояний нитяным дальномером используют рейки с сантиметровыми делениями, по которым берут отсчет l (число видимых в зрительную трубу сантиметров между проекциями дальномерных нитей). Дальномерное расстояние получают по формуле

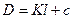, (85)

где K = 100 – коэффициент дальномера; с – постоянная нитяного дальномера (для большинства приборов с близка к нулю).

Точность нитяного дальномера примерно составляет 1:300 от измеренного расстояния. Длинные линии целесообразно измерять короткими отрезками длиной 50 – 100 м. Точность измерений в этом случае может достигать 1: 600 и даже 1:1000.

Чаще всего нитяный дальномер используют при определении дальномерных расстояний до точек при топографической (тахеометрической) съемке.

12.4. Электронный тахеометр

На рынке геодезических приборов имеется весьма большое количество геодезических приборов, называемых электронными тахеометрами, которые совмещают в себе функции теодолита и светодальномера. Далее рассмотрим особенности работы с электронным тахеометром Trimble 3305DR.

12.4.1. Назначение основных узлов и органов управления

На рис. 54 показаны внешние основные узлы и органы управления тахеометром.

Как определить угол наклона потолка?

Для подбора накладок на скошенный потолок вам необходимо знать диаметр основания светильника и угол наклона потолка, в статье расскажем про угол.

Несмотря на кажущуюся простоту вопроса, иногда вычисление угла наклона потолка вызывает некоторую сложность. Мы компания более чем клиентоориентированная, так что с удовольствием дадим пару вариантов как этот ваш угол мансардного потолка измерить. Перейти в Каталог продукции!

Способ первый и самый простой. В нашу цифровую эпоху многие пользуются смартфонами и в большинстве современных есть различные гироскопические датчики, в первую очередь это применяется в играх, чтобы определять положение телефона в пространстве ) но и для практических нужд этот функционал отлично применяется. Можно скачать (или просто открыть, например, на айфоне оно предустановлено) приложение и с его помощью простым прикладыванием к наклонной плоскости определить угол:

 Но даже тут есть маленький нюанс, если вы делаете замеры телефоном именно в точке будущего крепежа накладки, то все хорошо.
Но если вы делаете замер в какой-то другой точке потолка, то может появиться некоторая погрешность, т.к. маленькая площадь поверхности измерения, именно в этом месте может быть, например, какой-то изгиб, незаметный глазу. В этом случае лучше взять какую-нибудь пряму рейку, приложить ее к потолку и уже к ней прикладывать телефон:

Вот уже разницу в 1 градус получили ) К слову, посмотреть ассортимент изделий из заказать можно в разделе Каталог.

Есть еще вариант как сделать замер скоса потолка. Нам понадобится раздвижной транспортир и обычный уровень. Этот способ более сложный, но будет актуален, если под рукой нет смартфона )

Также есть еще вот такие уровни, прикладываете к плоскости и крутите шкалу пока не поймаете баланс, вот и покажет ваш угол:

Надеюсь вам это упростит задачу подбора накладок на скошенный потолок для светильников и люстр.

Угол наклона прямой — Concept

Угол наклона прямой — это угол, образованный пересечением прямой и оси x. Использование горизонтального «пробега» 1 и m для наклона, угла наклона, theta = tan-1 (м) или m = tan (theta). Следовательно, если угол или наклон известен, другой можно найти с помощью одного из уравнений. Если угол наклона отрицательный, то и наклон линии отрицательный.

Какой угол наклона лески? Итак, у меня есть линия, нарисованная здесь уравнением y = mx + b, оно должно быть вам знакомо. Это угол наклона тета, это угол между линией и горизонталью. Теперь я хочу выяснить, как я могу вычислить эту линию, как она соотносится с уравнением линии, поэтому я нарисовал здесь маленький треугольник, а затем я обозначу стороны, скажем, я обозначу это 1, что будет с этой стороны быть? Теперь я знаю, что наклон, наклон линии равен подъему над пробегом, поэтому наклон будет равен вопросительному знаку над 1, так что это будет наклон.
Теперь, если я посмотрю на этот прямоугольный треугольник, и это прямоугольный треугольник, я могу использовать тригонометрию прямоугольного треугольника, чтобы найти взаимосвязь между тета и m, верно? m — это длина по вертикали этой стороны, поэтому тангенс теты равен m по касательной к 1, тета равен m, так что это соотношение между углом наклона и наклоном, тангенс угла наклона — это наклон, а угол наклона равен арктангенс угла наклона, поэтому вы можете рассчитать наклон по углу наклона, а угол наклона можно рассчитать по углу наклона.
Теперь давайте посмотрим на другой, на несколько частных случаев. Горизонтальные или вертикальные линии. Теперь горизонтальная линия не обязательно будет пересекать ось x, конечно, для линии до y = 0 это ось x, но мы определяем ее угол наклона равным 0, и, конечно же, тангенс 0 равен 0, поэтому наклон будет касательной к 0, который равен 0, и это то, что мы, как мы определяем наклон горизонтальной линии, это 0.
А как насчет вертикальной? Что ж, я бы сказал, что здесь угол наклона пи больше 2, поэтому тета больше пи больше 2, каков наклон? Касательная к тэте, прямая касательная к пи более 2, но, конечно, это не определено, и это именно то, что мы хотели бы, чтобы наклон вертикальной линии не был определен, нет наклона, поэтому просто для просмотра, угол наклона линии угол, на который Линия определяет отношение к горизонтали, а наклон — это тангенс теты, угол наклона равен наклону, а угол наклона равен обратному тангенсу наклона.

.

Углы наклона и склонения

Уголки высоты / наклона и Углы депрессии / склонения Углы подъема или наклона углов над горизонтом, как если бы вы смотрели с уровня земли в вершина флагштока.Углы депрессии или склонения — это углы ниже горизонтали, как если бы вы смотрели из окна вниз на основание здание на соседнем участке. Всякий раз, когда у вас есть один из этих углов, вы следует сразу начать представлять, как прямоугольный треугольник впишется в описание. Движение по прямой ровный участок шоссе в Аризоне, вы заметите особенно высокий сагуаро («suh-WARH-oh») кактус прямо рядом с отметкой мили.Смотреть на одометре вы съезжаете ровно на двух десятых мили вниз по дороге. Извлекая из ствола теодолит вашего сына, вы измеряете угол высоты от вашего положения до вершины сагуаро как 2,4 ° . Какой рост у кактуса с точностью до ближайшего целого числа? Две десятых мили составляют 0,2 × 5280 футов = 1056 футов, так что это мое горизонтальное расстояние. Мне нужно найти высоту х кактуса.Итак, я рисую прямоугольный треугольник и маркирую все, что знаю: . Масштаб не важен; я не удосужившись получить угол «вправо». Я использую рисование как способ отслеживать информацию; конкретный размер не имеет значения. Что имеет отношение к , так это то, что У меня «противоположный» и «смежный» и угол мера.Это означает, что я могу создать и решить уравнение: До ближайшей ноги Сагуаро имеет высоту 44 футов. Вы запускали воздушного змея на обрыве, но вам как-то удалось сбросить кайт в озеро ниже.Вы знаете, что раздали 325 футов веревки. Геодезист сообщает вам, что угол склонения от ваше положение к кайту — 15 ° . Какова высота обрыва, на котором стоите вы с геодезистом? Сначала я рисую свой треугольник: Горизонтальная линия поперек верх — линия, от которой измеряется угол депрессии.Но по характеру параллельных линий такой же угол находится внизу. треугольник. Мне легче «увидеть» триггерные отношения в нижний треугольник, и высота немного более очевидна. Так Я буду использовать эту часть рисунка. У меня «противоположное», гипотенуза и угол, поэтому я буду использовать коэффициент синуса, чтобы найти рост. ч /325 = sin (15 °) авторское право © Элизабет Стапель 2010-2011 Все права защищены ч = 325 × sin (15 °) = 84,11618966 … Обрыв находится на высоте около 84 футов над озером. Маяк стоит на возвышенности 100 м над уровнем моря.Если ∠ACD измеряет 60 ° и ∠BCD равно 30 °, найти высоту маяка. Мне нужно выполнить это упражнение по шагам. Я не могу найти высоту башни, AB, пока у меня не будет длины базового компакт-диска.(Представьте, что D перемещается вправо, чтобы встретить продолжение AB, образуя прямоугольный треугольник.) Для этого вычисления я буду использовать высоту холма. Чтобы минимизировать ошибку округления, я буду использовать все цифры из моего калькулятора в моих вычислениях, и пытаюсь «унести» все вычисления в моем калькуляторе .. Теперь, когда у меня есть длина основания, Я могу найти общую высоту, используя угол, который измеряет высоту от уровня моря до вершины башни. Отлично! Сохраняя все цифры и проводя вычисления в своем калькуляторе, я получил точный ответ. Без округления! Но мне нужно вычесть, потому что «300» высота от воды до вершины башни. Первая сотня метров этой общей высоты — холм, итак: Вверх | Вернуться к индексу Цитируйте эту статью как: Стапель, Елизавета.«Углы наклона и склонения». Пурпурная математика . Доступна с https://www.purplemath.com/modules/incldecl.htm . Доступ [Дата] [Месяц] 2016 г.

НАЙТИ УРОК Этот урок можно распечатать для личного пользования.

.

Наклон линии | Аналитическая геометрия

4.3 Наклон прямой (EMBGD)

На диаграмме показано, что прямая линия составляет угол \ (\ theta \) с положительной осью \ (x \). Это называется углом наклона прямой линии.

Мы замечаем, что если градиент изменяется, то значение \ (\ theta \) также изменяется, поэтому угол наклона линии связан с ее градиентом. Мы знаем, что градиент — это отношение изменения направления \ (y \) к изменению направления \ (x \):

\ [m = \ frac {\ Delta y} {\ Delta x} \]

Из тригонометрии мы знаем, что тангенциальная функция определяется как отношение:

\ [\ tan \ theta = \ frac {\ text {противоположная сторона}} {\ text {смежная сторона}} \]

А из схемы видим, что

\ begin {align *} \ tan \ theta & = \ dfrac {\ Delta y} {\ Delta x} \\ \ поэтому m & = \ tan \ theta \ qquad \ text {for} \ text {0} \ text {°} \ leq \ theta <\ text {180} \ text {°} \ end {align *}

Следовательно, градиент прямой линии равен касательной к углу, образованному между прямой и положительным направлением оси \ (x \).

Вертикальные линии

• \ (\ theta = \ text {90} \ text {°} \)
• Градиент не определен, поскольку нет изменений в \ (x \) — значениях (\ (\ Delta x = 0 \)).
• Следовательно, \ (\ tan \ theta \) также не определено (график \ (\ tan \ theta \) имеет асимптоту в \ (\ theta = \ text {90} \ text {°} \)).

Горизонтальные линии

• \ (\ theta = \ text {0} \ text {°} \)
• Градиент равен \ (\ text {0} \), поскольку нет изменений в \ (y \) — значениях (\ (\ Delta y = 0 \)).
• Следовательно, \ (\ tan \ theta \) также равно \ (\ text {0} \) (график \ (\ tan \ theta \) проходит через начало координат \ ((\ text {0} \ text { °}; 0)) \).

Линии с отрицательными градиентами

Если прямая линия имеет отрицательный градиент (\ (m <0 \), \ (\ tan \ theta <0 \)), то угол, образованный между линией и положительным направлением оси \ (x \) - тупой.

Из диаграммы CAST в тригонометрии мы знаем, что функция касательной отрицательна во втором и четвертом квадранте.Если мы вычисляем угол наклона линии с отрицательным градиентом, мы должны добавить \ (\ text {180} \ text {°} \), чтобы изменить отрицательный угол в четвертом квадранте на тупой угол во втором квадранте. :

Если нам дана прямая с градиентом \ (m = — \ text {0,7} \), то мы можем определить угол наклона с помощью калькулятора:

\ begin {align *} \ tan \ theta & = m \\ & = — \ text {0,7} \\ \ поэтому \ theta & = \ tan ^ {- 1} (- \ text {0,7}) \\ & = — \ текст {35,0} \ текст {°} \ end {align *}

Этот отрицательный угол лежит в четвертом квадранте.Мы должны добавить \ (\ text {180} \) \ (\ text {°} \), чтобы получить тупой угол во втором квадранте:

\ begin {align *} \ theta & = — \ text {35,0} \ text {°} + \ text {180} \ text {°} \\ & = \ текст {145} \ текст {°} \ end {align *}

И мы всегда можем использовать наш калькулятор, чтобы проверить, что тупой угол \ (\ theta = \ text {145} \ text {°} \) дает градиент \ (m = — \ text {0,7} \).

Высокие оценки по математике — залог вашего успеха и будущих планов. Проверьте себя и узнайте больше о практике Сиявулы.

Зарегистрируйтесь и проверьте себя

Угол наклона

Упражнение 4.5

\ begin {align *} м & = \ загар \ тета \\ & = \ tan \ text {60} \ text {°} \\ \ поэтому m & = \ text {1,7} \ end {выровнять *}

\ begin {align *} м & = \ загар \ тета \\ & = \ tan \ text {135} \ text {°} \\ \ поэтому m & = — \ text {1} \ end {выровнять *}

\ begin {align *} м & = \ загар \ тета \\ & = \ tan \ text {0} \ text {°} \\ \ поэтому m & = \ text {0} \ end {выровнять *}

\ begin {align *} м & = \ загар \ тета \\ & = \ tan \ text {54} \ text {°} \\ \ поэтому m & = \ text {1,4} \ end {выровнять *}

\ begin {align *} м & = \ загар \ тета \\ & = \ tan \ text {90} \ text {°} \\ \ поэтому m & \ text {не определено} \ end {выровнять *}

\ begin {align *} м & = \ загар \ тета \\ & = \ tan \ text {45} \ text {°} \\ \ поэтому m & = \ text {1} \ end {выровнять *}

\ begin {align *} м & = \ загар \ тета \\ & = \ tan \ text {140} \ text {°} \\ \ поэтому m & = — \ text {0,8} \ end {выровнять *}

\ begin {align *} м & = \ загар \ тета \\ & = \ tan \ text {180} \ text {°} \\ \ поэтому m & = \ text {0} \ end {выровнять *}

\ begin {align *} м & = \ загар \ тета \\ & = \ tan \ text {75} \ text {°} \\ \ поэтому m & = \ text {3,7} \ end {выровнять *}

строка с \ (m = \ dfrac {3} {4} \)

\ begin {align *} \ tan \ theta & = m \\ & = \ frac {3} {4} \\ \ theta & = \ tan ^ {- 1} \ left (\ text {0,75} \ right) \\ \ поэтому \ theta & = \ text {36,8} \ text {°} \ end {выровнять *}

\ begin {align *} 2у — х & = 6 \\ 2у & = х + 6 \\ y & = \ frac {1} {2} x + 3 \\ \ tan \ theta & = m \\ & = \ frac {1} {2} \\ \ theta & = \ tan ^ {- 1} \ left (\ text {0,5} \ right) \\ \ поэтому \ theta & = \ text {26,6} \ text {°} \ end {выровнять *}

линия проходит через точки \ ((- 4; -1) \) и \ ((2; 5) \)

\ begin {align *} m & = \ frac {y_2 — y_1} {x_2 — x_1} \\ & = \ frac {5 + 1} {2 + 4} \\ & = \ frac {6} {6} \\ \ поэтому m & = 1 \\ \ тан \ тета & = 1 \\ \ theta & = \ tan ^ {- 1} \ left (\ text {1} \ right) \\ \ поэтому \ theta & = \ text {45} \ text {°} \ end {выровнять *}

\ begin {align *} х & = 3у + \ гидроразрыва {1} {2} \\ x — \ frac {1} {2} & = 3y \\ \ frac {1} {3} x — \ frac {1} {6} & = y \\ \ поэтому m & = \ frac {1} {3} \\ \ theta & = \ tan ^ {- 1} \ left (\ frac {1} {3} \ right) \\ \ поэтому \ theta & = \ text {18,4} \ text {°} \ end {выровнять *}

линия проходит через точки \ ((2; 5) \) и \ ((\ frac {2} {3}; 1) \)

\ begin {align *} m & = \ frac {y_2 — y_1} {x_2 — x_1} \\ & = \ frac {1–5} {\ frac {2} {3} -2} \\ & = \ frac {-4} {- \ frac {4} {3}} \\ \ поэтому m & = 3 \\ \ theta & = \ tan ^ {- 1} \ left (\ text {3} \ right) \\ \ поэтому \ theta & = \ text {71,6} \ text {°} \ end {выровнять *}

линия с градиентом, равным \ (\ text {0,577} \)

\ begin {align *} m & = \ text {0,577} \\ \ theta & = \ tan ^ {- 1} \ left (\ text {0,577} \ right) \\ \ поэтому \ theta & = \ text {30} \ text {°} \ end {выровнять *}

Рабочий пример 8: Наклон прямой

Определите угол наклона (с точностью до десятичного знака \ (\ text {1} \)) прямой, проходящей через точки \ ((2; 1) \) и \ ((- 3; -9) \) .

Нарисуйте эскиз

Назначить переменные координатам заданных точек

\ [x_1 = 2; \ qquad y_1 = 1; \ qquad x_2 = -3; \ qquad y_2 = -9 \]

Определите уклон линии

\ begin {align *} m & = \ frac {y_2 — y_1} {x_2 — x_1} \\ & = \ frac {-9-1} {- 3-2} \\ & = \ frac {-10} {- 5} \\ \ поэтому m & = 2 \ end {align *}

Используйте градиент, чтобы определить угол наклона линии

\ begin {align *} \ tan \ theta & = m \\ & = 2 \\ \ поэтому \ theta & = \ tan ^ {- 1} 2 \\ & = \ текст {63,4} \ текст {°} \ end {align *}

Важно: убедитесь, что ваш калькулятор находится в режиме DEG (градусов).

Напишите окончательный ответ

Угол наклона прямой равен \ (\ text {63,4} \) \ (\ text {°} \).

Рабочий пример 9: Наклон прямой

Определите уравнение прямой, проходящей через точку \ ((3; 1) \) с углом наклона \ (\ text {135} \ text {°} \).

Используйте угол наклона для определения градиента линии

\ begin {align *} м & = \ загар \ тета \\ & = \ tan \ text {135} \ text {°} \\ \ поэтому m & = -1 \ end {align *}

Запишите градиентно-точечную форму уравнения прямой линии

\ [y — y_1 = m (x — x_1) \]

Заменитель \ (m = -1 \)

\ [y — y_1 = — (x — x_1) \]

Заменить данную точку \ ((3; 1) \)

\ begin {align *} у — 1 & = — (х — 3) \\ у & = -x + 3 +1 \\ & = -x + 4 \ end {align *}

Напишите окончательный ответ

Уравнение прямой: \ (y = -x + 4 \).

Рабочий пример 10: Наклон прямой

Определите острый угол (с точностью до десятичного знака \ (\ text {1} \)) между линией, проходящей через точки \ (M (-1; 1 \ frac {3} {4}) \) и \ (N (4; 3) \) и прямая \ (y = — \ frac {3} {2} x + 4 \).

Нарисуйте эскиз

Проведите линию через точки \ (M (-1; 1 \ frac {3} {4}) \) и \ (N (4; 3) \) и линию \ (y = — \ frac {3} { 2} x + 4 \) на подходящей системе осей. Метки \ (\ alpha \) и \ (\ beta \), углы наклона двух линий.Обозначьте \ (\ theta \) острый угол между двумя прямыми линиями.

Обратите внимание, что \ (\ alpha \) и \ (\ theta \) — острые углы, а \ (\ beta \) — тупой угол.

\ [\ begin {array} {rll} \ hat {B} _1 & = \ text {180} \ text {°} — \ beta & (\ angle \ text {on str. line}) \\ \ text {and} \ theta & = \ alpha + \ hat {B} _1 \ quad & (\ text {ext.} \ angle \ text {of} \ треугольник = \ text {sum int. opp}) \\ \ поэтому \ theta & = \ alpha + (\ text {180} \ text {°} — \ beta) \\ & = \ text {180} \ text {°} + \ alpha — \ beta \ конец {массив} \]

Используйте градиент, чтобы определить угол наклона \ (\ beta \)

Из уравнения \ (y = — \ frac {3} {2} x + 4 \) мы видим, что \ (m <0 \), поэтому \ (\ beta \) - тупой угол такой, что \ (\ text {90} \ text {°} <\ beta <\ text {180} \ text {°} \).{-1} \ left (- \ frac {3} {2} \ right) & = - \ text {56,3} \ text {°} \ end {выровнять *}

Этот отрицательный угол лежит в четвертом квадранте. Мы знаем, что угол наклона \ (\ beta \) — это тупой угол, который лежит во втором квадранте, поэтому

\ begin {align *} \ beta & = — \ text {56,3} \ text {°} + \ text {180} \ text {°} \\ & = \ текст {123,7} \ текст {°} \ end {align *}

Определите уклон и угол наклона линии через \ (M \) и \ (N \)

Определить градиент \ begin {align *} m & = \ frac {y_2 — y_1} {x_2 — x_1} \\ & = \ dfrac {3 — \ frac {7} {4}} {4 — (- 1)} \\ & = \ dfrac {\ frac {5} {4}} {5} \\ & = \ frac {1} {4} \ end {align *}

Определить угол наклона \ begin {align *} \ загар \ альфа & = м \\ & = \ frac {1} {4} \\ \ поэтому \ alpha & = \ tan ^ {- 1} \ left (\ frac {1} {4} \ right) \\ & = \ текст {14,0} \ текст {°} \ end {align *}

Напишите окончательный ответ

\ begin {align *} \ theta & = \ text {180} \ text {°} + \ alpha — \ beta \\ & = \ text {180} \ text {°} + \ text {14,0} \ text {°} — \ text {123,7} \ text {°} \\ & = \ текст {70,3} \ текст {°} \ end {align *}

Острый угол между двумя прямыми равен \ (\ text {70,3} \) \ (\ text {°} \).{-1} \ left (- \ frac {9} {2} \ right) \\ & = — \ текст {77,5} \ текст {°} \\ \ поэтому \ theta & = \ text {180} \ text {°} — \ text {77,5} \ text {°} \\ \ поэтому \ theta & = \ text {102,5} \ text {°} \ end {выровнять *}

линия, проходящая через \ ((- 1; -6) \) и \ ((- \ frac {1} {2}; — \ frac {11} {2}) \)

\ begin {align *} m & = \ frac {y_2 -y_1} {x_2 — x_1} \\ & = \ frac {- \ frac {11} {2} + 6} {- \ frac {1} {2} +1} \\ & = \ frac {\ frac {1} {2}} {\ frac {1} {2}} \\ \ поэтому m & = 1 \\ \ theta & = \ tan ^ {- 1} \ left (1 \ right) \\ \ поэтому \ theta & = \ text {45} \ text {°} \ end {выровнять *}

\ begin {align *} 5 & ​​= 10л — 15х \\ 5 + 15x & = 10у \\ \ frac {1} {2} + \ frac {3} {2} x & = y \\ \ поэтому m & = \ frac {3} {2} \\ \ theta & = \ tan ^ {- 1} \ left (\ frac {3} {2} \ right) \\ \ поэтому \ theta & = \ text {56,3} \ text {°} \ end {выровнять *}

\ begin {align *} m & = \ frac {y_2 -y_1} {x_2 — x_1} \\ & = \ frac {3 + 1} {2–0} \\ & = \ frac {4} {2} \\ \ поэтому m & = 2 \\ \ theta & = \ tan ^ {- 1} \ left (2 \ right) \\ \ поэтому \ theta & = \ text {63,4} \ text {°} \ end {выровнять *}

\ begin {align *} m & = \ frac {y_2 -y_1} {x_2 — x_1} \\ & = \ frac {2 — 0} {0 — 6} \\ & = \ frac {2} {- 6} \\ \ поэтому m & = — \ frac {1} {3} \\ \ theta & = \ tan ^ {- 1} \ left (- \ frac {1} {3} \ right) \\ \ поэтому \ theta & = — \ text {18,4} \ text {°} \\ \ поэтому \ theta & = \ text {180} \ text {°} — \ text {18,4} \ text {°} \\ \ поэтому \ theta & = \ text {161,6} \ text {°} \ end {выровнять *}

Градиент undefined

Определите острый угол между прямой, проходящей через точки \ (A (-2; \ frac {1} {5}) \) и \ (B (0; 1) \), и прямой, проходящей через точки \ ( C (1; 0) \) и \ (D (-2; 6) \).{-1} \ влево (-2 \ вправо) \\ \ поэтому \ alpha & = — \ text {63,4} \ text {°} \\ \ поэтому \ alpha & = \ text {180} \ text {°} — \ text {63,4} \ text {°} \\ \ поэтому \ alpha & = \ text {116,6} \ text {°} \\ \ text {And} \ theta & = \ beta + (\ text {180} \ text {°} — \ alpha) \ quad (\ text {ext.} \ angle \ треугольник) \\ \ поэтому \ theta & = \ text {21,8} \ text {°} + (\ text {180} \ text {°} — \ text {116,6} \ text {°}) \\ & = \ текст {85,2} \ текст {°} \ end {выровнять *}

Определите угол между линией \ (y + x = 3 \) и линией \ (x = y + \ frac {1} {2} \).{-1} \ left (1 \ right) \\ \ поэтому \ beta & = \ text {45} \ text {°} \\ \ text {And} \ theta & = \ beta + (\ text {180} \ text {°} — \ alpha) \ quad (\ text {ext.} \ angle \ треугольник) \\ \ поэтому \ theta & = \ text {45} \ text {°} + (\ text {180} \ text {°} — \ text {135} \ text {°}) \\ & = \ текст {90} \ текст {°} \ end {выровнять *}

Найдите угол между прямой \ (y = 2x \) и прямой, проходящей через точки \ ((- 1; \ frac {7} {3}) \) и \ ((0; 2) \).

Пусть угол наклона прямой \ (y = 2x \) равен \ (\ beta \), а угол наклона другой линии равен \ (\ alpha \).{-1} \ left (2 \ right) \\ \ поэтому \ beta & = \ text {63,4} \ text {°} \\ m & = \ frac {y_2 -y_1} {x_2 — x_1} \\ & = \ frac {2 — \ frac {7} {3}} {0 + 1} \\ & = \ frac {- \ frac {1} {3}} {1} \\ \ поэтому m & = — \ frac {1} {3} \\ \ поэтому \ alpha & = — \ text {18,4} \ text {°} \\ \ поэтому \ alpha & = \ text {180} \ text {°} — \ text {18,4} \ text {°} \\ \ поэтому \ alpha & = \ text {161,6} \ text {°} \\ \ text {And} \ theta & = \ beta + (\ text {180} \ text {°} — \ alpha) \ quad (\ text {ext.} \ угол \ треугольник) \\ \ поэтому \ theta & = \ text {63,4} \ text {°} + (\ text {180} \ text {°} — \ text {161,6} \ text {°}) \\ & = \ текст {81,8} \ текст {°} \ end {выровнять *} .

Как определить валентный угол в молекуле?

Химия

Наука

• Анатомия и физиология
• Астрономия
• Астрофизика
• Биология
• Химия
• наука о планете Земля
• Наука об окружающей среде
• Органическая химия

.