Как обозначать площадь: «Что такое площадь в математике 2 класс четырехугольника?» – Яндекс.Знатоки – формулы расчета для разных фигур, знаки обозначения, единицы измерения

Как вычислить площадь: формулы расчета для разных фигур, знаки обозначения, единицы измерения

Знания о том, как измерить Землю, появились еще в древности и постепенно оформились в науку геометрию. С греческого языка это слово так и переводится — «землемерие».

Мерой протяжённости плоского участка Земли по длине и ширине является площадь. В математике она обычно обозначается латинской буквой S (от англ. «square» — «площадь», «квадрат») или греческой буквой σ (сигма). S обозначает площадь фигуры на плоскости или площадь поверхности тела, а σ площадь поперечного сечения провода в физике. Это основные символы, хотя могут быть и другие, например, в сфере сопротивления материалов, А — площадь сечения профиля.

Формулы расчета

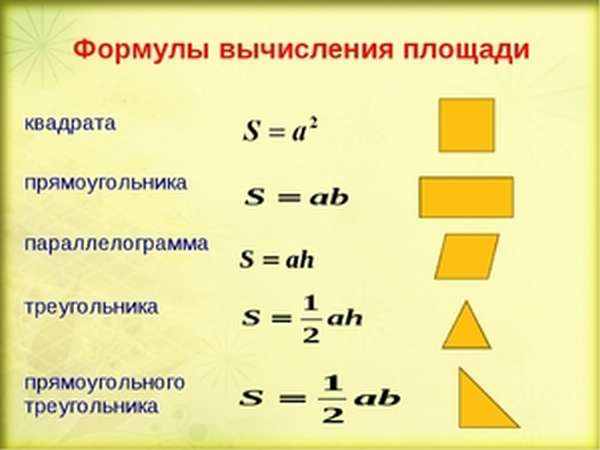
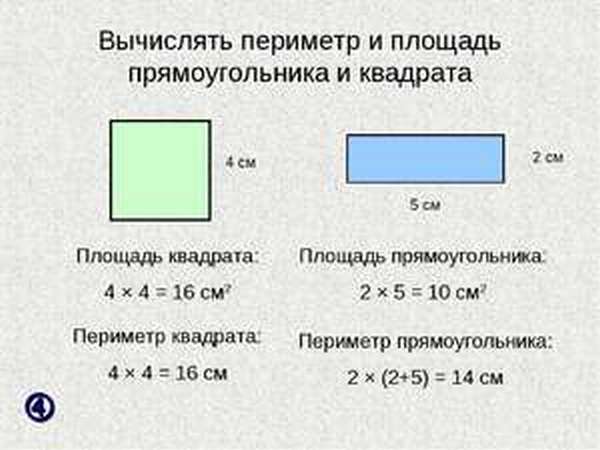Зная площади простых фигур, можно находить параметры более сложных. Античными математиками были выведены формулы, по которым можно легко их вычислять. Такими фигурами являются треугольник, четырёхугольник, многоугольник, круг.

Чтобы найти площадь сложной плоской фигуры, её разбивают на множество простых фигур, таких как треугольники, трапеции или прямоугольники. Затем математическими методами выводят формулу для площади этой фигуры. Подобный метод используют не только в геометрии, но и в математическом анализе для вычисления площадей фигур, ограниченных кривыми.

Это интересно: какой вектор называется разностью двух векторов?

Треугольник

Начнём с самой простой фигуры — треугольника. Они бывают прямоугольные, равнобедренные и равносторонние. Возьмём любой треугольник ABC со сторонами AB=a, BC=b и AC=c (∆ ABC). Чтобы найти его площадь, вспомним известные из школьного курса математики теоремы синусов и косинусов. Отпуская все выкладки, придём к следующим формулам:

• S=√[p•(p-a)•(p-b)•(p-c)] — известная всем формула Герона, где p=(a+b+c)/2 — полупериметр треугольника,
• S=a•h/2, где h — высота, опущенная на сторону a,
• S=a•b•(sin γ)/2, где γ — угол между сторонами a и b,
• S=a•b/2, если ∆ ABC — прямоугольный (здесь a и b — катеты),
• S=b²•(sin (2•β))/2, если ∆ ABC — равнобедренный (здесь b — одно из «бёдер», β — угол между «бёдрами» треугольника),
• S=a²•√¾, если ∆ ABC — равносторонний (здесь a — сторона треугольника).

Это интересно: Как найти периметр треугольника.

Четырёхугольник

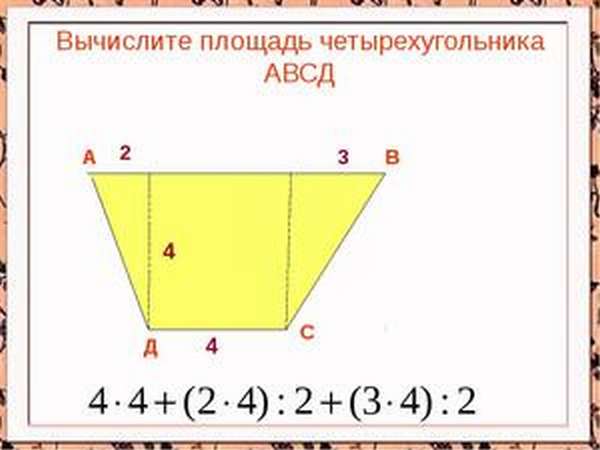
Пусть имеется четырёхугольник ABCD, у которого AB=a, BC=b, CD=c, AD=d. Чтобы найти площадь S произвольного 4-угольника, нужно разделить его диагональю на два треугольника, площади которых S1 и S2 в общем случае не равны.

Затем по формулам вычислить их и сложить, т. е. S=S1+S2. Однако, если 4-угольник принадлежит к определённому классу, то его площадь можно найти по заранее известным формулам:

• S=(a+c)•h/2=e•h, если 4-угольник — трапеция (здесь a и c — основания, e — средняя линия трапеции, h — высота, опущенная на одно из оснований трапеции,
• S=a•h=a•b•sin φ=d1•d2•(sin φ)/2, если ABCD — параллелограмм (здесь φ — угол между сторонами a и b, h — высота, опущенная на сторону a, d1 и d2 — диагонали),
• S=a•b=d²/2, если ABCD — прямоугольник (d — диагональ),
• S=a²•sin φ=P²•(sin φ)/16=d1•d2/2, если ABCD — ромб (a — сторона ромба, φ — один из его углов, P — периметр),
• S=a²=P²/16=d²/2, если ABCD — квадрат.

Многоугольник

Чтобы найти площадь n-угольника, математики разбивают его на простейшие равные фигуры —треугольники, находят площадь каждого из них и затем складывают. Но если многоугольник относится к классу правильных, то используют формулу:

S=a•n•h/2=a²•n/[4•tg (180°/n)]=P²/[4•n•tg (180°/n)], где n — количество вершин (или сторон) многоугольника, a — сторона n-угольника, P — его периметр, h — апофема, т. е. отрезок, проведённый из центра многоугольника к одной из его сторон под углом 90°.

Круг

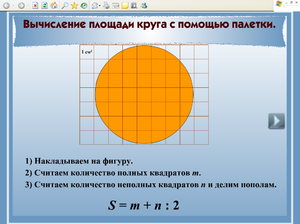Круг — это совершенный многоугольник, имеющий бесконечное число сторон

. Нам необходимо вычислить предел выражения справа в формуле площади многоугольника при числе сторон n, стремящемуся к бесконечности. В этом случае периметр многоугольника превратится в длину окружности радиуса R, которая будет границей нашего круга, и станет равен P=2•π•R. Подставим это выражение в указанную выше формулу. Мы получим:

S=(π²•R²•cos (180°/n))/(n•sin (180°/n)).

Найдём предел этого выражения при n→∞. Чтобы это сделать, учтём, что lim (cos (180°/n)) при n→∞ равен cos 0°=1 (lim — знак предела), а lim [1/(n•sin (180°/n))]= lim [1/(n•sin (π/n))] при n→∞ равен 1/π (мы перевели градусную меру в радианную, используя соотношение π рад=180°, и применили первый замечательный предел lim (sin x)/x=1 при x→∞). Подставив в последнее выражение для S полученные значения, придём к известной формуле:

S=π²•R²•1•(1/π)=π•R².

Единицы измерения

Применяются системные и внесистемные единицы измерения. Системные единицы относятся к СИ (Система Интернациональная). Это квадратный метр (кв. метр, м²) и единицы, производные от него: мм², см², км².

В квадратных миллиметрах (мм²), например, измеряют площадь сечения проводов в электротехнике, в квадратных сантиметрах (см²) — сечения балки в строительной механике, в квадратных метрах (м²) — квартиры или дома, в квадратных километрах (км²) — территории в географии.

Однако иногда используются и внесистемные единицы измерения, такие, как: сотка, ар (а), гектар (га) и акр (ас). Приведём следующие соотношения:

• 1 сотка=1 а=100 м²=0,01 га,
• 1 га=100 а=100 соток=10000 м²=0,01 км²=2,471 ас,
• 1 ас= 4046.856 м²=40,47 а=40,47 соток=0,405 га.

Что такое площадь в математике? Единицы площади :: SYL.ru

Есть проблемы с элементарной геометрией? Эта статья поможет вам решить одну из них. Здесь вы узнаете о том, что такое площадь в математике, об единицах ее измерения и других важных аспектах этой темы. Разбор некоторых конкретных примеров даст вам возможность глубже изучить вопрос.

Что такое площадь в математике?

Площадь — это мера того, сколько пространства есть на плоской поверхности. Например, есть два одинаковых куска бумаги, чья суммарная площадь, очевидно, больше чем у каждого из них по отдельности.

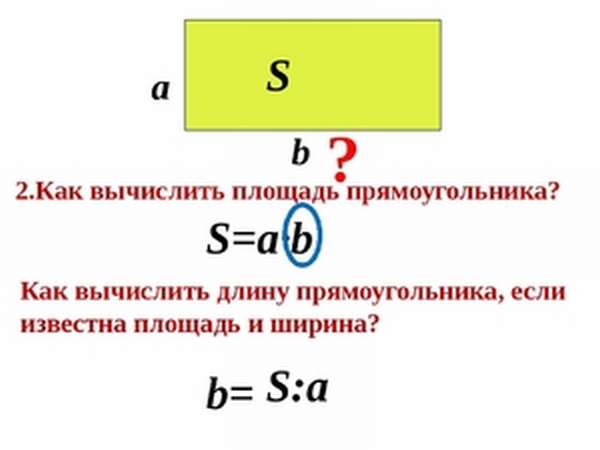
Площади фигур в математики вычисляются разными путями, зависимо от их формы. Например, в случае с прямоугольником необходимо найти произведение его высоты и ширины. Посмотрим на рисунок.

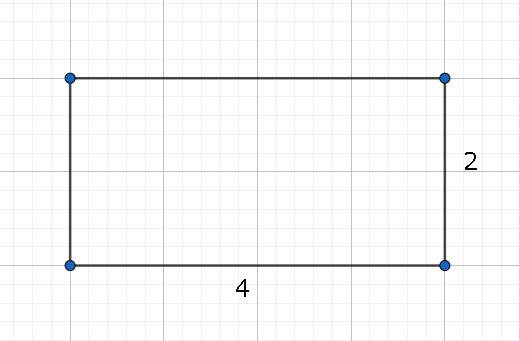
Имеем ответ: 2 × 4 = 8 см². Задача решена.

Проверить его можно вручную подсчитав количество больших квадратиков внутри прямоугольника. Подобной задачи достаточно для того чтобы объяснить, что такое площадь в математике. Но в этой теме есть еще и другие важные нюансы.

Единица измерения площади в математике

Измеряется площадь в квадратных единицах. То есть ее можно определить как некоторое количество четырехугольников, чьи стороны равны 1. При этом если поменять местами значения длины и высоты, конечный результат не изменится.

Примечание! Все величины должны быть в одинаковых единицах измерения.

Допустим, что данные заданы в сантиметрах. Как тогда правильно обозначить это на бумаге?

Вместо того чтобы писать «восемь квадратных сантиметров», можно использовать запись вида «8 см²«. Достаточно просто возвести сокращенную форму меры во вторую степень.

Перевод величин

У студента или ученика может возникнуть потребность перевести значение из одних единиц измерения в другие. Существует только один верный способ это сделать. Правда, для этого необходимо вспомнить, как правильно переводить одни единицы измерения в другие.

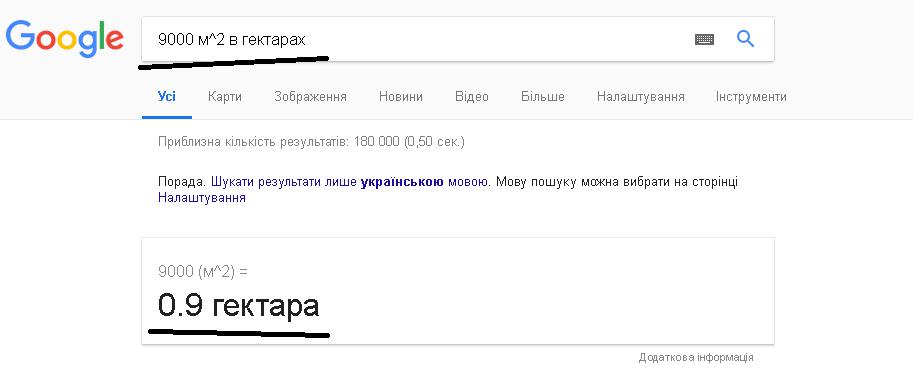
Допустим имеем 9000 м². Нужно найти, сколько это гектаров. Известно что 1 га = 10 000 м². Разделим исходную площадь на десять тысяч. В результате получим 0,9 га. Это и будет искомым значением. Главное иметь информацию об отношении двух величин между собой.

А теперь проверим.

Другие фигуры

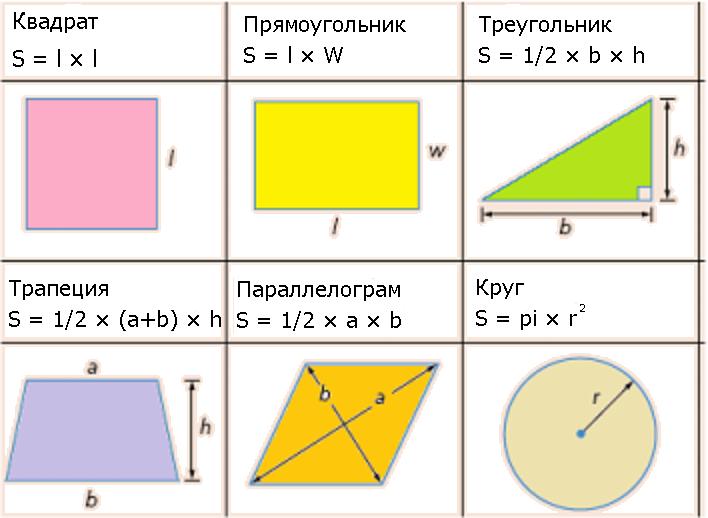
К сожалению, для нахождения площади не всегда достаточно перемножить два числа. Ситуации бывают разные. Рабочая формула для каждой из них будет видоизменяться из раза в раз. Ниже приведены наиболее часто встречаемые вариации фигур.

Пример

Теперь вы знаете, что такое площадь в математике. Основной теоретический материал усвоен, и можно переходить к практике. Для закрепления решим конкретную задачу.

Условие. Имеется квадрат со стороной 3 сантиметра и круг с радиусом такой же длины. Найдите, чья площадь больше и на сколько.

Решение. Для начала произведем вычисления для каждой из фигур по отдельности:

S_квад = 3 × 3 = 9. Итак, площадь квадрата равна 9 см².

А вот площадь круга вычисляется уже по другой формуле. Для ее нахождения необходимо вспомнить значение ∏:

S_круг = ∏ × 3 × 3 ≈ 28,26 см².

По результатам видим, что площадь круга в несколько раз больше. Осталось лишь посчитать на сколько. Для этого найдем разницу двух чисел.

S_круг — S_квад = 28,26 — 9 = 19,26 см².

Ответ найден.

Обычно, решая такие задачи, человек должен сводить все к готовым формулам. Затем уже искать неизвестные, выражать величины одну через другую и использовать смекалку.

Что такое периметр и площадь — Topkin

Периметр – это геометрический термин, который часто встречается в задачах. Чтобы понять, что такое периметр, следует нарисовать произвольный многоугольник и вооружиться линейкой. В переводе с греческого языка этот термин обозначает «измеряю вокруг».

Как вычислить периметр

Периметр обозначается латинской буквой P

. Его можно измерить в сантиметрах, миллиметрах, метрах или дециметрах. Чтобы узнать периметр, следует измерить длину всех сторон многоугольника. Полученные значения нужно сложить. Итоговая сумма и станет ответом на вопрос: «Чему равен периметр многоугольника».

Периметр – это длина линий, которые ограничивают замкнутую фигуру (квадрат, прямоугольник, треугольник и др.).

Например, перед вами многоугольник со сторонами 10, 12, 13 и 11 см. Складываем вышеназванные числа (10+12+13+11) и получаем сумму 46. Это и есть периметр многоугольника.

Для удобства вычисления периметра в геометрии существует ряд формул. Каждая формула соответствует определенной фигуре.

Периметр и площадь квадрата

Это сумма его четырех сторон. Как мы знаем, все стороны квадрата имеют равный размер. Поэтому мы можем узнать периметр квадрата, умножив длину его стороны на четыре:

P= a*4

P= a+a+a+a

Например, перед нами квадрат со стороной 10 см.

P= 10*4

P=40

Ответ: 40 см

P= 10+10+10+10

P=40

Ответ: 40 см

Чтобы разобраться, что такое периметр и площадь, следует уяснить, что периметр вычисляет длину контура фигуры, а площадь – размер всей ее поверхности.

Чтобы узнать площадь квадрата, необходимо воспользоваться простой формулой:

S= a*a

S=a²

S – это площадь, а – сторона квадрата.

Например, в задаче указано, что длина стороны квадрата составляет 10см.

S=10*10

S= 100см²

Ответ: 100см²

Периметр и площадь прямоугольника

Стороны прямоугольника, находящиеся друг напротив друга и имеющие одинаковую длину, называются противолежащими. Это длина и ширина, они условно обозначаются латинскими буквами a и b. Формула для вычисления периметра прямоугольника выглядит так:

P= (a+b)*2

Используя эту формулу, мы сначала находим сумму ширины и длины, а затем умножаем ее на два.

Например, перед нами прямоугольник, имеющий длину 6 см и ширину 2 см.

P= (6+2) * 2

P= 16

Ответ: 16 см

Чтобы узнать площадь прямоугольника, следует длину умножить на ширину. Формула выглядит так:

S= a*b

Например, в условиях задачи сказано, что прямоугольник имеет длину 5 см и ширину 2см. Меняем буквы a и b на указанные числа.

S= 5*2

S=10см²

Ответ: 10 см²

Периметр круга (длина окружности)

Каждый круг имеет центр. Расстояние от центра круга до любой точки, расположенной на окружности, имеет название радиус круга. Часто ученики путают понятия «круг» и «окружность» и пытаются определить площадь окружности. Это серьезная ошибка. Следует разделить в голове понятия «круг» и «окружность». У окружности нет и не может быть площади, у нее есть только длина.

Чтобы найти периметр круга, следует вычислить длину его окружности. Существует формула для нахождения длины окружности:

L = 2πr

L= 2πd

L – длина окружности

π – это число «пи», математическая константа. Она равна отношению длины окружности к длине ее диаметра. Древнее название числа «пи» – лудольфово число. Это число иррационально, его десятичное представление после точки никогда не заканчивается.

 π = 3.141 592 653 589 793 238 462 643 383 279 502

Для удобства вычислений обычно используют значение 3.14

R

– это радиус окружности

D – Диаметр окружности

Итак, чтобы определить периметр круга, надо найти произведение радиуса и 2π. Если в задаче указан диаметр, то

Например, перед нами круг с радиусом 3 см. Найдем его периметр.

L= 2*3,14*3

L=6π

L=6*3.14

L = 18.84 см

P_к= 18,84 см

Ответ: 18.84 см

Отличие периметра от площади

Площадь – это размер поверхности фигуры, а периметр – это сумма ее границ.

Площадь всегда измеряется в квадратных единицах (см

2, м², мм²). Периметр измеряется в единицах длины – в сантиметрах, миллиметрах, метрах, дециметрах.

Порядок величины (площадь) — Википедия

Материал из Википедии — свободной энциклопедии

Площади различных порядков могут быть сопоставлены для визуального представления их относительности. Данные, приведённые ниже, должны рассматриваться как «типичные величины», расчётные величины округлены.

Единицей площади в Международной системе единиц является 1 квадратный метр (обозначение единицы величины — м², буквенное обозначение величины в уравнениях и формулах — A), производный от основной единицы — метра.

Также используются производные единицы площади:

• 1 мм² (квадратный миллиметр) = 0,000001 м²
  (1 000 000 мм² = 1 м²)
• 1 см² (квадратный сантиметр) = 0,0001 м²
  (10 000 см² = 1 м²)
• 1 а (ар) = 100 м²
• 1 га (гектар) = 100 а = 10 000 м²
• 1 км² (квадратный километр) = 100 га = 1 000 000 м²

1 мкм² (квадратный микрометр) = 1 000 000 нм² (квадратных нанометров)

• 0,05 мкм² — Поверхность вируса гриппа
• 0,20 мкм² — граница видимости оптического микроскопа
• 500 мкм² — Поверхность бактерии

1 мм² (квадратный миллиметр) = 1 000 000 мкм² (квадратных микрометров)

• 0,01 мм² — наименьшая уловимая невооружённым глазом частица
• 0,15 мм² — поверхность человеческой яйцеклетки
• 0,196 мм² — площадь поперечного сечения графитной палочки механического карандаша (0,5 мм)

• 25 мм² — клетка бумаги в клеточку (обычная 5-миллиметровая клетка)
• 49 мм² — клетка бумаги в клеточку (крупная 7-миллиметровая клетка)
• 55 мм² — средняя барабанная перепонка человека (pars tensa)

• 11,40 см² — отверстие сингла (грамофонной пластинки/7″)
• 17,50 см² — спичечная коробка (50 мм × 35 мм)
• 46,21 см² — международный формат чековой карточки по ISO/IEC 7810 (85,60 мм × 53,98 мм)
• 50,27 см² — поверхность мяча для настольного тенниса
• 53,70 см² — игральная карта (стандартный формат)
• 74,40 см² — 5-евровая банкнота (120 мм × 62 мм)
• 89,92 см² — подставка под пивной бокал (круглая, 107 мм в диаметре)
• 97,50 см² — 50-, 100- и 500-рублёвая банкноты (150 мм × 65 мм)
• 97,66 см² — средняя человеческая ладонь

• 1 м² — листа DIN-A0, 841 мм × 1189 мм
• 1,5—2 м² — поверхность кожи взрослого человека
• 2,23 м² — ворота хоккея с шайбой
• 3,5 м² — рулон туалетной бумаги (10 см × 14 см × 250 листов)
• 4,16 м² — стол для настольного тенниса
• 6 м² — гандбольные ворота
• 9 м² — типичная садовая беседка (3 м × 3 м)

• 12,5 м² — стояночное место (5,0 м × 2,5 м)
• 17,86 м² — футбольные ворота (7,32 м × 2,44 м)
• 37,16 м² — ринг
• 25—80 м² — типичная жилая площадь небольшой городской квартиры
• 81,74 м² — площадка для игры в бадминтон

• 10,18 миллиона км² — Европа (континент)
• 13,20 миллиона км² — Антарктида (континент)
• 13,20 миллиона км² — бывший Арабский халифат (при Омейядах) около 750 г.
• 13,50 миллиона км² — бывшая Французская колониальная империя около 1919 г.
• 13,70 миллиона км² — Испанская колониальная империя около 1740 г.
• 14,09 миллиона км² — Северный Ледовитый океан
• 17,13 миллиона км² — Россия с Крымом (крупнейшее государство в мире)
• 17,84 миллиона км² — Южная Америка
• 17,95 миллиона км² — поверхность Плутона
• 23,02 миллиона км² — поверхность Тритона, крупнейшего спутника Нептуна
• 24,46 миллиона км² — бывшая Российская империя в 1866 г.
• 24,93 миллиона км² — Северная Америка
• 29,18 миллиона км² — Африканский союз
• 30,30 миллиона км² — Африка
• 33,00 миллиона км² — бывшая Британская империя около 1921 г. и Монгольская империя около 1274 г.
• 37,93 миллиона км² — поверхность Луны
• 44,61 миллиона км² — Азия
• 73,43 миллиона км² — Индийский океан (без окраинных морей)
• 74,76 миллиона км² — поверхность Меркурия
• 82,40 миллиона км² — Атлантический океан (без окраинных морей)
• 83,32 миллиона км² — поверхность Титана, крупнейшего спутника Сатурна
• 85,00 миллиона км² — Афроевразия (крупнейшая непрерывная суша в мире)
• 87,18 миллиона км² — поверхность Ганимеда, крупнейшего спутника в Солнечной системе

• 144,6 миллиона км² — поверхность Марса
• 149,1 миллиона км² — поверхность суши Земли
• 166,2 миллиона км² — Тихий океан (без окраинных морей)
• 361,1 миллиона км² — водная поверхность Земли
• 460,2 миллиона км² — поверхность Венеры
• 510,1 миллиона км² — поверхность Земли

• 7,620 миллиарда км² — поверхность Нептуна
• 8,083 миллиарда км² — поверхность Урана

10 миллиардов км² — 100 миллиардов км²[править | править код]

• 42,61 миллиарда км² — поверхность Сатурна
• 61,42 миллиарда км² — поверхность Юпитера

• 463,2 миллиарда км² — плоскость, заключённая в пределах орбиты Луны вокруг Земли

• 6,087 триллиона км² (6,09 · 10¹⁸ м²) — поверхность Солнца
• 70,31 триллиона км² (7,03 · 10²² м²) — плоскость, заключённая в пределах орбиты Земли вокруг Солнца
• 106,2 триллиона км² (1,06 · 10²⁶ м²) — плоскость, заключённая в пределах орбиты Плутона вокруг Солнца

Площадь прямоугольника ℹ️ обозначение и единицы измерения, способы определения, основные правила и формулы, примеры вычислений

Общие сведения

В различных задачах с физико-математическим уклоном приходится вычислять площадь прямоугольника. Однако формула расчета применяется не только в математике и физике, но и во время ремонтных работ. Например, следует посчитать количество расходных материалов, которое зависит от квадратуры комнаты или здания.

Очень важно не только знать основные соотношения, но и корректно переводить единицы измерения из одной в другую. От знаний полностью зависит экономия денежных средств. Например, при клейке обоев в комнате требуется определенное количество рулонов. Это количество можно купить в строительном магазине «на глаз» или рассчитать квадратуру комнаты. Во втором случае можно существенно сэкономить. Для того чтобы посчитать квадратные метры помещения, нужно вычислить его площадь.

Площадь фигуры

Площадью двумерной фигуры является численная характеристика, которая показывает ее размерность. Она обозначается литерой S и измеряется в квадратных единицах (мм ², см ², дм ²и т. д.). Не каждый элемент геометрии имеет площадь. Прямая, луч, отрезок, точка не имеют двумерной размерности. Фигуры, у которых она присутствует, являются квадратируемыми. Если значения их S равны, то они являются равновеликими.

Для вычисления значения двухплоскостной размерности фигуры применяется интегральный метод. Однако бывают частные случаи, когда вычислять интеграл необязательно. Существуют определенные формулы, полученные с помощью интегрального метода. Чтобы ими воспользоваться, нужно просто подставить числовые значения сторон.

Нахождение площади получило широкое распространение в физике. Например, для вычисления электрического сопротивления нужно найти площадь поперечного сечения проводника. Она зависит от его формы. Площадь можно вычислить и у объемной поверхности, но для этого применяется интегрирование.

Единицы измерения

При решении задач на нахождение значения площади нужно знать единицы ее измерения. Кроме того, следует правильно выполнять перевод одной единицы в другую. В системе исчисления используются квадратичные единицы измерения. За основу следует брать размер стороны прямоугольника. Например, при указании площади в кв. м нужно измерять в метраже стороны объекта. Это стандартная единица измерения площади.

Существуют также производные единицы. Самой маленькой из них является квадратный миллиметр (кв. мм или мм ²). В некоторой литературе или программировании можно встретить такую запись: sqr (m), которая означает квадратный метр. Основные производные единицы площади:

1. 1 см ² = 100 мм ².

2. 1 дм ² = 100 см ².

3. 1 м ² = 100 дм ² = 10000 см ².

4. 1 км ² = 1000000 м ².

5. 1 ар (а) = 1 сотка = 100 м ².

6. 1 гектар (га) = 10000 м ².

Последние применяются для измерения земельного участка. Однако необязательно их все помнить. Они легко выводятся при помощи простейших математических вычислений. Например, для выполнения расчетов нужно перевести кв. м в кв. см. Однако человек мог забыть, сколько см ²в квадратном метре. Следует взять метрическую форму (1 м = 100 см). Затем нужно возвести обе части выражения в квадрат: 1 м ² = 100 * 100 = 10000 (см ²).

Информация о прямоугольнике

Прямоугольник — четырехугольная геометрическая фигура, противолежащие стороны которой равны и углы являются прямыми. Частным случаем данной фигуры считается квадрат. У него все углы прямые, а также все стороны равны между собой. Для выполнения расчетов нужно знать основные соотношения, свойства и признаки.

Важным аспектом является идентификация фигуры и применение к ней формул и соотношений. В двухмерной геометрии, которую еще называют эвклидовой, можно встретить необычный признак, позволяющий определить принадлежность четырехугольника к прямоугольнику. Его формулировка следующая: достаточно хотя бы трех углов, равных 90 градусам, чтобы четырехугольник считался прямоугольником.

Утверждение легко доказывается. Это связано с тем, что по теореме о сумме внутренних углов произвольного четырехугольника, составляющей 360 градусов, четвертый угол тоже равен 90. Нужно выполнить следующие расчеты для определения градусной меры четвертого угла: D = 360 — (90 + 90 + 90) = 90. Необходимо отметить, что смежные с ними углы равны 90.

Свойства и признаки

Очень часто новички путают свойства и признаки фигуры. Однако это совсем различные понятия. Признаками фигуры называются характерные особенности, которые позволяют отнести ее к тому или иному классу. Свойства — совокупность аксиом, позволяющих использовать некоторые данные при решении или доказательстве теорем и тождеств. Прямоугольник обладает следующими признаками:

1. Условие параллельности и равенства противоположных сторон.
2. Наличие четырех прямых углов.
3. Равенство диагоналей.
4. Квадрат диагонали равен суммарному значению квадратов двух сторон, которые не противоположны.
5. Все стороны не равны между собой.

Очень важно уметь различать геометрические фигуры. Поскольку прямоугольник является параллелограммом, то их часто путают. Основное его отличие — это равенство всех углов 90 градусов. У параллелограмма и ромба углы будут равняться 90 в том случае, когда они являются квадратами. Последний отличается от искомой фигуры (прямоугольника) равенством всех сторон. Поскольку прямоугольник является частным случаем параллелограмма, то обладает такими же свойствами:

1. Углы равны между собой 90 градусов.
2. Противолежащие параллельные стороны равны.
3. Сумма всех внутренних углов составляет 360.
4. Диагональ, проведенная внутри прямоугольника, делит его на два равнозначных треугольника, которые являются равновеликими. Они равны по третьему признаку равенства треугольников (размерности сторон одной фигуры равны значениям сторон другой фигуры).
5. Треугольники, полученные при проведении двух диагоналей, равны по всем признакам (углам и сторонам).
6. Диагонали пересекаются между собой в точке, которая делит их на четыре равные части.
7. Точка пересечения диагоналей — центр симметрии.
8. Сумма квадратов двух диагоналей соответствует суммарному значению квадратов всех сторон фигуры.

Однако свойств и признаков фигуры недостаточно для решения задач. Следует знать основные соотношения и формулы.

Периметр и размерность

Нужно ввести некоторые обозначения. Пусть стороны прямоугольника АВСД обозначаются литерами a и b. Поскольку диагонали равны, то можно только обозначить размерность одной буквой «d». Периметром называется сумма всех сторон заданной фигуры. Он обозначается литерой P. Для его нахождения применяется формула такого вида: P = 2 * (a + b). Однако бывает случай, когда известна только одна его сторона и диагональ. Формула приобретает следующий вид: P = 2a + [2 * (2d ² — 2a ² )]^(1/2) и P = 2b + [2 * (2d ² — 2b ² )]^(1/2).

Чтобы вычислить площадь прямоугольника, следует воспользоваться таким соотношением: S = a * b. Эта базовая формула, которая используется также в строительной сфере и физике. Однако существует еще один способ, с помощью которого можно узнать площадь прямоугольника. Она находится с помощью формулы Герона для треугольников с площадями S1 и S2, а затем результат умножается на 2. Эта особенность основывается на свойстве фигуры, поскольку диагональ делит его на два равных треугольника.

Соотношение имеет следующий вид: S = S1 + S2 = 2S1= 2 * [p * (p — a) * (p — b) * (p — d)]^(1/2). Переменная «p» — полупериметр треугольника. Он находится таким методом: p = P / 2 = (a + b + d) / 2.

Примеры решения

Задачи на нахождение площади применяются в нескольких дисциплинах. В геометрии применяются различные комбинации, при которых известны некоторые величины:

1. Две стороны.
2. Одна из сторон и диагональ.
3. Диагональ и разность сторон.

Для расчета расходных материалов и площади поперечного сечения проводника можно всегда измерить стороны прямоугольника. Существует два способа нахождения: автоматизированный и ручной. В первом случае используется специализированное программное обеспечение. Однако вовсе не обязательно применять сложные алгоритмы и программные модули, поскольку формула является очень простой. Для расчета специалисты рекомендуют применять онлайн-калькулятор.

При ручном режиме расчета нужно подставлять значения в формулу. После этого выполнять вычисления. Возможна и оптимизация процесса вычисления. Для этой цели рекомендуется использовать Excel. Приложение входит в состав стандартного офисного пакета MS Office.

Геометрия на плоскости

Задача сводится к тому, что необходимо высчитать S, зная размеры сторон (a = 25 и b = 10). В этом случае следует воспользоваться базовой формулой: S = a * b = 25 * 10 = 250 (ед ²). В ответе указывается условная единица измерения, поскольку явная не указана в условии задачи.

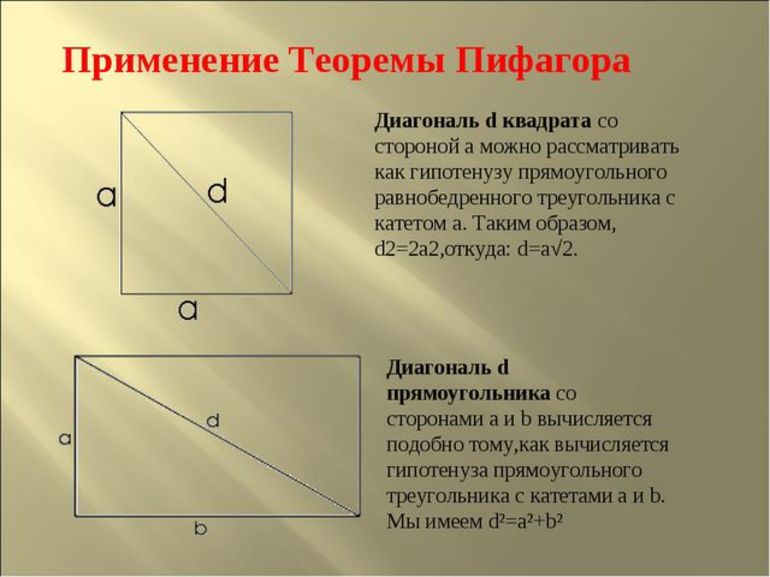
Еще один вариант задания немного сложнее предыдущего. Он имеет следующее условие: одна из сторон прямоугольника равна 6 м и диагональ 10 м. Нужно найти площадь прямоугольника. Формулой в этом случае является теорема Пифагора. Треугольник, который образуется при проведении диагонали, считается прямоугольный (неравносторонний, а разносторонний). Решается задача следующим образом:

1. Находится неизвестная сторона: b =(d ² — a ²)^(1/2) = (100 — 36)^(1/2) = 8 (м).

2. Площадь (произведение сторон): S = 6 * 8 = 48 (м ²).

Можно использовать двойную формулу Герона, однако метод усложняет вычисления. Для сравнения скорости и объема вычислений следует решить задачу вторым способом:

1. Сторона: b = 8 (м).

2. Значение площади будет вычисляться таким образом: S = 2 * [12 * (12−6) * (12−8) * (12−10)]^(1/2) = 2 * 24 = 48 (м ²).

Второй способ считается неправильным, поскольку необходимо во всех задачах оптимизировать вычисления. Сложным типом задачи, кроме интегрирования, считается нахождение площади, когда неизвестны стороны, а известна только диагональ (10). Известно также, что одна из сторон больше другой на 3 метра. В этом случае надо выражать одну сторону через другую. Алгоритм решения следующий:

1. Обозначить стороны: a = x и b = x — 3.
2. Составить уравнение: x * (x — 3) = 10.

3. Раскрыть скобки: x ² — 3x — 10 = 0.

4. Нахождение дискриминанта: D = b ² — 4* a * c = 9 — (4 * 10) < 0.

Поскольку у уравнения корней нет, то и прямоугольника с такими данными не существует. Если же корни имеются, то нужно подставить их для нахождения стороны b.

Электротехника и ремонт

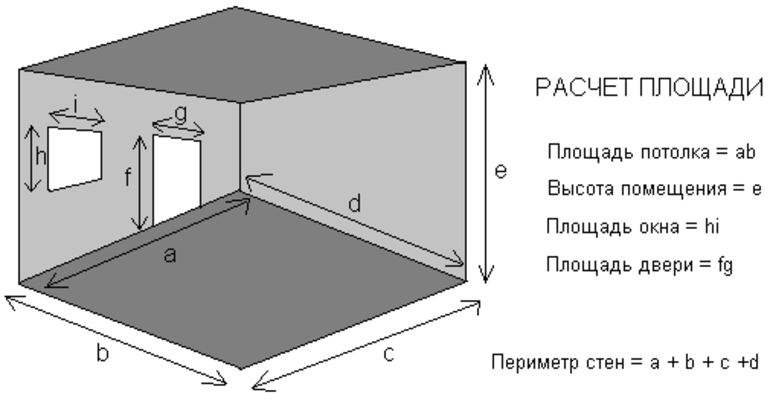
Определение площади поперечного сечения проводника необходимо для вычисления сопротивления. В этом случае нужно измерить длину и толщину формы проводника, а затем перемножить стороны между собой. Если он является полым, то площадь фигуры нужно искать с помощью интеграла. Для разных проводников существуют определенные формулы.

Для вычисления расходных материалов нужно искать площадь потолка, стен, комнат или дома. Распространенный пример подсчета квадратуры керамической плитки для санузла: размер комнаты составляет 2,5х1,5 метра. Для подсчета необходимо воспользоваться формулой определения площади комнаты: S = 2,5 * 1,5 = 3,75 (м ²). Однако берется не исходное значение, а приближенное. Его нужно округлять только в большую сторону, т. е. править 3,75 на значение 4. Следует руководствоваться таким правилом: результат округляется в большую сторону.

Таким образом, для расчета площади прямоугольника можно воспользоваться формулой, а не выполнять интегрирование. Однако перед этим нужно внимательно изучить основные понятия и математические отношения.