Как измерить правильно угол – Транспортир ℹ️ как правильно пользоваться математическим инструментом, инструкция по измерению и построению углов, функции, виды прибора

Транспортир ℹ️ как правильно пользоваться математическим инструментом, инструкция по измерению и построению углов, функции, виды прибора

Люди обычно сталкиваются с транспортирами в математике, когда учатся в школе создавать точные геометрические фигуры. Возможно, у многих из них никогда больше не будет причин снова использовать эти приборы, тем не менее транспортиры имеют долгую историю применения в различных областях.

История изобретения

Происхождение этого математического инструмента восходит к жрецам в Египте и Вавилоне, которые установили меру углов в градусах, минутах и секундах. Однако до времён классической Греции тригонометрия не использовалась в математике.

Во втором веке до нашей эры астроном Гиппарх из Никии изобрёл тригонометрический стол, для измерения треугольников. Затем Птолемей включил в свою великую астрономическую книгу «Альмагест» таблицу, с угловыми приращениями от 0 до 180°, с погрешностью менее 1/3600 единиц. Он также объяснил метод составления этой таблицы, и на протяжении всей книги приводил много примеров того, как вычислять с помощью неё неизвестные элементы фигур.

Птолемей также был автором, так называемой теоремы Менелая для решения сферических треугольников, и на протяжении многих веков его тригонометрия была основным пособием для астрономов.

Возможно, в то же время, учёные Индии также разработали тригонометрическую систему, основанную на функции синуса, которая, в отличие от используемого в настоящее время синуса, была не пропорцией, а длиной стороны, противоположной углу в прямом треугольнике этой гипотенузы. Индийские математики использовали разные значения для этого в своих таблицах.

Томас Бландевиль рассказал о приборе специально созданном, для рисования и измерения фигур в своём «Кратком описании универсальных карт» 1589 года. Как видно из названия, он применял его, чтобы править навигационные карты для использования в высоких широтах.

Другие европейские математики также описывали подобные приборы примерно в то же время. Независимо от того, кто первым придумал этот инструмент, к началу XVII века он вошёл в стандартную практику мореплавателей и геодезистов. К XVIII веку транспортиры начали появляться в учебниках по геодезии и геометрии.

Транспортиры в современном понимании возникли во второй половине XVIII века, когда такие учёные, как Джесси Рамсден и Георг Фридрих Брандер, усовершенствовали ранее созданные устройства.

В то время предпочтительными материалами для их изготовления были:

• дерево;
• латунь;
• серебро;
• медь;
• слоновая кость.

В первой половине XX века начали применять олово и целлулоид.

Называться транспортиром (рус.) прибор стал в 1610 году. Термин произошёл от средневекового слова protractor, что означает «переносить», который, в свою очередь, произошел от латинского слова protrahere «тянуть вперёд».

Разновидности и использование

Транспортир — это простой гониометр для измерения или создания угла. Он выглядит как круглый или полукруглый диск с делением. Диск может быть изготовлен из пластика, прочной бумаги или листового металла. Типичными являются диаметры от 8 до 15 см и деления на 1° и 0,5°, при измерении также 0,5 Гон (новый градус). Точность составляет от 0,1 до 0,5° в зависимости от диаметра шкалы. Более точные приборы имеют поворотную рейку со шкалой (длина до миллиметра).

Частично из-за различного использования их изготавливают во многих формах: знакомый полукруг, а также круги, прямоугольники, квадраты или четверть круга (квадранты). Они также могут иметь различные диаметры. Их изготавливают из латуни, стали, дерева, слоновой кости или пластика. Самой распространённой формой является полукруг с ограничительной шкалой в 180 градусов.

Угловой транспортир — градуированный круглый инструмент с одной поворотной рукой; используется для измерения или разметки. В строительстве часто требуется отмерить угол в 90 градусов. Иногда прилагается шкала Вернье, чтобы дать более точные показания. Прибор широко применяется для изготовления архитектурных и механических чертежей, хотя его использование уменьшилось с появлением современного программного обеспечения для рисования.

Универсальные транспортиры скоса используются изготовителями инструментов; поскольку они делают измерения посредством механического контакта с предметом, то классифицируются как механические транспортиры.

Угловой транспортир применяется для того, чтобы измерить и проверить углы с очень жёсткими допусками. Он считывает до 5 угловых минут (5 или 1/12°) и может измерять от 0 до 360°.

Сегодня также применяются электронные приборы, которые обычно работают с поворотным датчиком. Кроме того, связанными с транспортиром приборами являются:

• теодолит;
• оптический транспортир в строительной промышленности и геодезии;
• инклинометр для определения уклонов и косвенной альтиметрии;
• секстант для навигации.

Измерение градусов угла

Для того чтобы научиться пользоваться транспортиром инструкция нужна на начальном этапе. Для его освоения достаточно нескольких минут и примеров (смотреть онлайн) того, как можно измерить и построить угол с помощью этого прибора.

Измерить угол, значит найти его величину. Углы разделяют на три типа: острый, тупой и прямой. Прямоугольный имеет 90 градусов. Все углы что имеют больше этого значения называются тупыми, и соответственно меньше 90 градусов называются острыми. Развёрнутый угол имеет 180 градусов.

Понимание того, что углы являются частями окружностей, полезно, потому что тогда конструкция транспортира обретает смысл. Поскольку полный круг имеет 360º, отдельный угол должен быть меньше этого числа, потому что он часть круга.

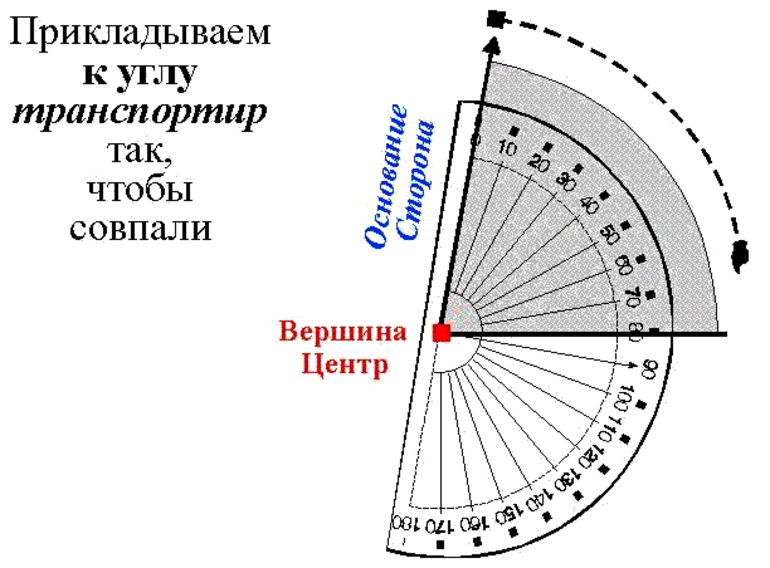
Алгоритм измерения следующий: для того чтобы измерить угол транспортиром необходимо приложить его центр верхней кромки линейки к вершине измеряемого угла. Вершина — это точка, в которой две из трёх сторон треугольника пересекаются.

Нижнюю планку (основание) транспортира нужно выставить горизонтально. Каждый транспортир имеет точку, спроектированную в центре основания, Эта средняя точка располагается на вершине угла, который должен быть измерен или нанесён на график. Другая сторона должна пересекать транспортир в одной из точек его дуги.

Если вторая сторона (линия) до дуги не доходит нужно продолжить её с помощью простой или масштабной линейки. То число, на шкале дуги, которое будет пересечено линией и есть величина угла в градусах.

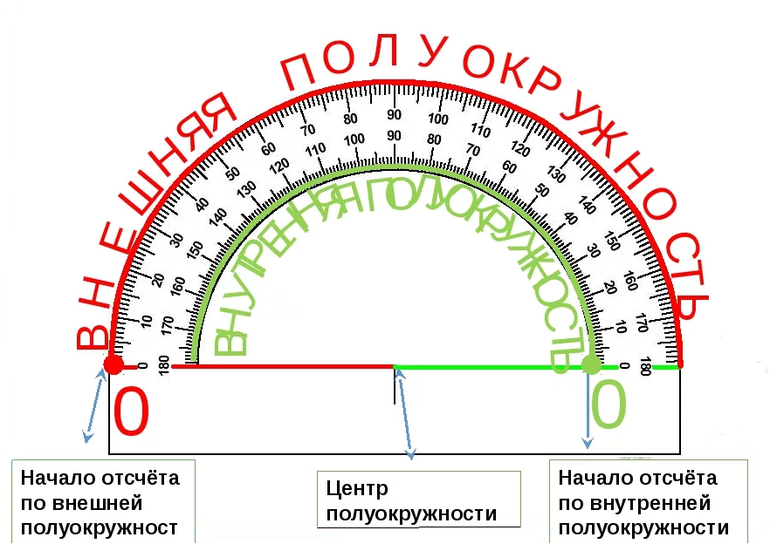
Для удобства на большинстве транспортиров сделано две шкалы, внутренняя и внешняя, которые отображают числа в каждой строке.

Построение угла

Берётся чистый лист бумаги в клетку. На нём карандашом отмечается точка, от которой проводиться прямая линия, как одна из сторон будущего угла. Эта черта служит для того, чтобы задать направление второй стороне. В простых упражнениях, для приобретения навыка построения угла, линия проводится горизонтально.

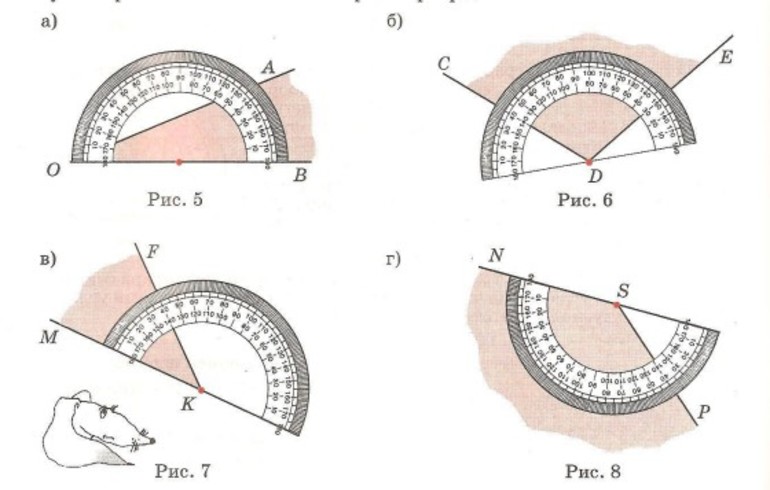
Центр основы транспортира располагается на любом из концов черты, который будет вершиной угла. Эта точка отмечается на бумаге карандашом. И именно к этому месту, внутри отверстия и присоединяется вершина угла, одна из сторон которого должна совпадать в горизонтальной плоскости с внутренней стороной линейки транспортира.

Затем на шкале отмечается необходимый градус. С внутренней стороны отверстия также обозначается точка возле этого градуса. И от вершины проводится прямая линия к этой точке. Таким образом, получается необходимый угол.

Для того чтобы правильно пользоваться транспортиром очень важно его выровнять, и точно прикладывать, для получения верных измерений.

Пересечённые линии в верхней части прямой кромки линейки должны совпадать с вершиной (конечной точкой), где соединяются два луча.

Измерение углов. Транспортир. Видеоурок. Математика 5 Класс

Какие-то вещи можно измерить, какие-то нельзя. Например, нельзя измерить дружбу или любовь. А расстояние, вес, температуру вполне можно. Чтобы что-то измерять, нужно всем договориться о единицах измерения.

Метр, дюйм, аршин – это и есть такие договоренности при измерении длины. Эталонный метр хранится во Франции, в Палате мер и весов. Килограмм, фунт, пуд – это договоренности для измерения массы. Эталонный килограмм тоже хранится в Палате мер и весов.

Единицы измерения придуманы для конкретных величин. В секундах не измерить вес, а в аршинах – время.

В геометрии такая же ситуация. Есть сантиметры, для измерения длин отрезков, но они не подходят для измерения углов. Для измерения углов есть свои единицы измерения. На этом уроке мы рассмотрим одну из них, а именно градусы.

Разделим полный угол на 360 равных частей. Для этого удобно использовать окружность. Поделим ее на 360 частей и соединим каждое полученное деление с центром. Получим 360 равных углов (см. Рис. 1).

Рис. 1. Окружность, разделенная на 360 равных углов

Один такой маленький угол назовем углом в 1° (см. Рис. 2).

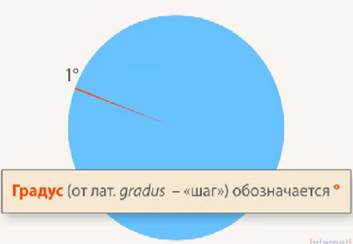
Рис. 2. 1 градус

Не важно, какого размера будет окружность, которую мы делим. Поделим обе окружности на 360 частей, получим равные углы в 1°, хотя стороны одного угла визуально длиннее, чем у другого (см. Рис. 3).

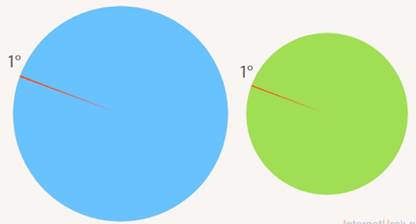
Рис. 3. Углы равны

Стороны углов можно продолжать бесконечно, от этого размер угла не меняется (см. Рис. 4).

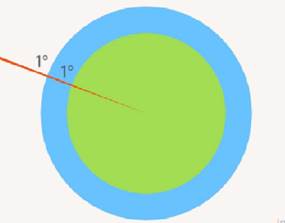
Рис. 4. Более явный пример равенства углов

Величина любого угла – это сколько раз в него умещается угол в 1°.

Вот мы видим угол 13° (см. Рис. 5).

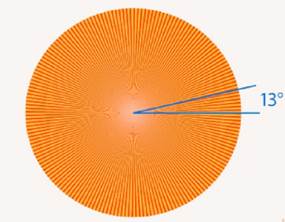
Рис. 5. Угол 13°

Понятно, что полный угол состоит из 360 таких углов. То есть он равен 360° (см. Рис. 6).

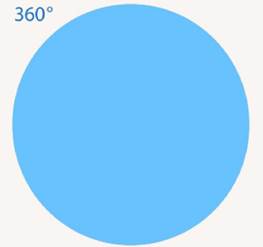
Рис. 6. Полный угол

Развернутый угол – это половина полного угла. Он равен 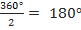 (см. Рис. 7).

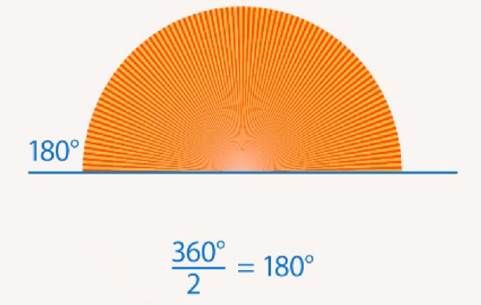
Рис. 7. Развернутый угол

Прямой угол является половиной развернутого и равен 90° (см. Рис. 8).

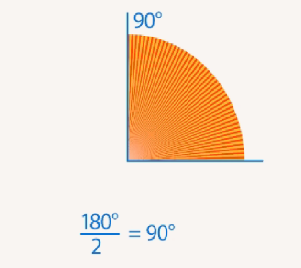
Рис. 8. Прямой угол

Эталон градуса нет нужды где-то хранить. Если нужно, то всегда можно полный угол разделить на 360 частей, или развернутый – на 180, или прямой – на 90.

Линейка нужна для того, чтобы измерить имеющийся отрезок или начертить отрезок нужной длины. Чтобы измерить угол или начертить угол нужной величины, мы тоже используем линейку, только не прямую, а круглую. Она называется транспортиром (см. Рис. 9).

Рис. 9. Транспортир

Единицы измерения на ней – градусы. Шкала начинается с нуля и заканчивается 180°.То есть максимальный угол, который мы можем измерить или начертить, – это 180°, развернутый.

Транспортиры могут быть разных размеров, но это не влияет на то, какого размера углы ими измеряют. Для более крупного транспортира у углов нужно чертить стороны длиннее.

1. Измерим пару углов.

Прямая часть транспортира совмещается с одной стороной угла, центр транспортира с вершиной угла. Смотрим, где оказалась вторая сторона угла, – 54° (см. Рис. 10, 11).

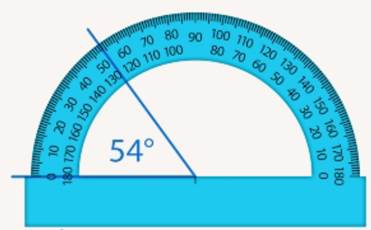
Рис. 10. Измерение угла

Проделаем то же самое со вторым углом, 137°.

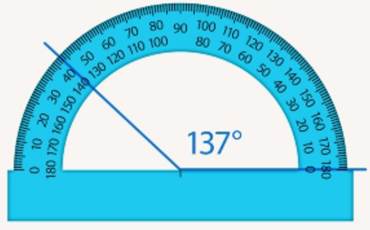
Рис. 11. Измерение угла

Если сторона угла не достает до шкалы, то ее нужно сначала продлить.

2. Начертим углы 29°, 81° и 140°.

Сначала чертим одну сторону угла по линейке (см. Рис. 12).

Рис. 12. Построение одной стороны угла

Отмечаем вершину. Совмещаем с транспортиром. Отмечаем точкой нужное значение угла – 29° (см. Рис. 13).

Рис. 13. Использование транспортира для построения углов

Убираем транспортир. Соединяем полученную точку с вершиной (см. Рис. 14).

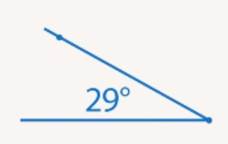
Рис. 14. Угол 29°

Точно так же строим два других угла (см. Рис. 15).

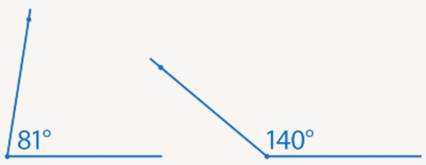
Рис. 15. Построение углов

Итак, мы с вами обсудили, что для измерения углов люди договорились использовать градусы. Градус – это 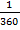 полного угла.

Инструментом для измерения и построения углов является транспортир.

Можно не использовать названия углов – полный, развернутый, прямой. Мы можем просто говорить – 360 градусов, 180 или 90 градусов.

На самом деле бывает, когда мы одни величины измеряем единицами, казалось бы, для них не предназначенными, «чужими» единицами.

Можно ли измерить расстояние в минутах? Да, мы часто используем этот способ. «От моего дома до школы 5 минут». Если быть точнее, то «5 минут пешком». Мы здесь используем известную всем величину – скорость пешехода. И величина «5 минут» на самом деле означает «расстояние, которое пешеход проходит за 5 минут». Скорость пешехода – 5 км/ч, 5 минут – это 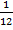 часа, умножим одно на другое. Получаем примерно 400 метров. Не очень точно, зато удобно.

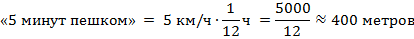
Точно по такому же принципу устроена другая единица измерения расстояния – световой год. Световой год – расстояние, которое проходит свет за 1 год. С помощью этой единицы меряют расстояния между звездами.

Очень распространенный пример использования «чужой» единицы измерения – это измерять вес в килограммах. На самом деле килограмм – единица измерения массы, а вес – это другая физическая величина. Если хотите подробнее узнать, в чем разница между массой и весом, и почему измерять вес в килограммах не верно, то наберите в поисковой системе «масса и вес» и получите множество пояснений по этому поводу.

Атмосферное давление мы до сих пор измеряем в миллиметрах (миллиметрах ртутного столба).

Хотя для угла есть свои «родные» единицы измерения – градусы, которые мы и проходим на этом уроке, все-таки его можно измерять и с помощью линейных величин, например сантиметров. Если нужно измерить угол 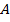, то можно достроить его до треугольника, так чтобы один угол был прямым, и разделить длину одной стороны на другую.

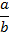
Получим величину угла 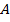, которая называется тангенсом.

Если увеличить треугольник, то ничего не изменится (см. Рис. 16).

  

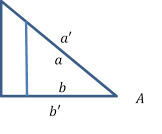
Рис. 16. Тангенс

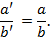
Ведь во сколько раз увеличилась одна сторона, во столько и вторая.

То есть величины часто можно измерять «чужими» единицами, но это чуть сложнее, там нужны некоторые дополнительные договоренности.

Существуют и другие единицы измерения углов.

1.        Минуты и секунды.

Как и метр можно делить на дециметры, сантиметры, миллиметры для более точных измерений, так и градусы делятся на более мелкие единицы измерения.

Если угол в 1° разделить на 60 равных частей, то величина полученного угла называется минута, 1′.

Если минуту поделить на 60 частей, то полученная величина называется секундой. Секунда – уже очень маленькая величина, но ее тоже можно делить дальше.

Почему вообще стали делить на 360 частей полный угол, ведь это не очень удобно? В древнем Вавилоне была шестидесятеричная система (у нас десятеричная). Им было удобно делить на 60.

2.        Грады.

Чтобы сделать измерение углов ближе к нашей десятичной системе счисления, были предложены грады. Для этого прямой угол делится на 100 частей. Полученная величина называется град. Полный угол составляет тогда 400 градов. Система не прижилась, и сейчас ее не используют.

3.        Радиан.

Если взять два радиуса окружности так, чтобы кусочек окружности между ними тоже был равен радиусу, то угол между радиусами мы и примем за новую единицу измерения. Он называется 1 рад (радиан). Эта мера используется наравне с градусной. У нее есть свои преимущества и свои недостатки по сравнению с градусами (см. Рис. 17).

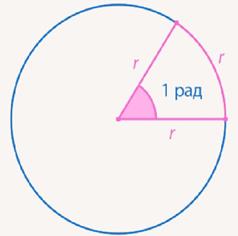
Рис. 17. Радианы

Например, теперь полный угол (вся окружность) состоит не из целого числа единичных углов. Полный угол состоит из 6 с лишним единичных углов. Не очень удобно, зато теперь длина дуги (части окружности) и угол хорошо связаны. Если взять окружность радиуса 1 см, то величина угла совпадает с длиной дуги. Угол 1 рад – дуга 1 см, угол 2 рад – длина дуги 2 см.

 

Список литературы

1. Зубарева И.И., Мордкович А.Г. Математика. 5 класс. – М.: Мнемозина, 2013.
2. Виленкин Н.Я. и др. Математика. 5 кл. – М.: Мнемозина, 2013.
3. Ерина Т.М. Математика 5кл. Раб. тетрадь к уч. Виленкина, 2013. – М.: Мнемозина, 2013.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Shkolo.ru (Источник).
2. Cleverstudents.ru (Источник).
3. Festival.1september.ru (Источник).

 

Домашнее задание

1. Зубарева И.И., Мордкович А.Г. Математика. 5 класс. – М.: Мнемозина, 2013. Стр. 144 № 522.
2. Начертите углы: 23°, 167°, 84°.
3. Ершова А.П., Голобородько В.В. Самостоятельные и контрольные работы по математике для 5 класса (5-е изд.) – 2010. Стр. 163 № 3.

Как правильно измерить угол

1.15. ИЗМЕРЕНИЕ ДИРЕКЦИОННЫХ УГЛОВ ПО КАРТЕ

Измерение транспортиром. Тонко очиненным карандашом, аккуратно по линейке, прочерчивают линию через главные точки условных знаков исходного пункта и ориентира. Длина прочерченной линии должна быть больше радиуса транспортира, считая от точки ее пересечения с вертикальной линией координатной сетки. Затем совмещают центр транспортира с точкой пересечения и поворачивают его, сообразуясь с величиной угла, как показано на рис. 27. Отсчет против прочерченной линии при положении транспортира, указанном на рис. 27, а, будет соответствовать величине дирекционного угла, а при положении транспортира, указанном на рис. 27,6, к полученному отсчету необходимо прибавить 180°.

При измерении дирекционного угла необходимо помнить, что дирекционный угол отсчитывается от северного направления вертикальной линии сетки по ходу часовой стрелки.

Средняя ошибка измерения дирекционного угла транспортиром, имеющимся на командирской линейке, примерно равна 1°. Большим транспортиром (с радиусом 8—10 см) угол на карте можно измерить со средней ошибкой 15′.

Рис. 27. Измерение дирекционных углов транспортиром

Измерение хордоугломером (рис. 28). Через главные точки условных знаков исходного пункта и ориентира проводят на карте тонкую прямую линию длиной не менее 12 см. Из точки пересечения этой линии с вертикальной линией сетки карты циркулем делают на них засечки радиусом, равным расстоянию на хордоугло-мере от 0 до 10 больших делений. Засечки делают на линиях, образующих острый угол.

Затем измеряют хорду — расстояние между отметками отложенных радиусов. Для этого левую иглу циркуля-измерителя с отложенной хордой передвигают по крайней левой вертикальной линии шкалы хордоугломера до тех пор, пока правая игла циркуля не совпадет с каким-либо пересечением наклонной и горизонтальной линии. При этом правую иглу необходимо передвигать строго на одном уровне с левой. В таком положении циркуля производят отсчет против его правой иглы. По верхней части шкалы отсчитывают большие и десятки малых делений. По левой части шкалы с ценой делений 0-01 уточняют величину угла. Пример измерения угла хордоугломером показан на рисунке.

С помощью хордоугломера измеряют острый угол от ближайшей вертикальной линии координатной сетки, а дирекционный угол отсчитывают от северного направления линии сетки по ходу часовой стрелки. Значение дирекционного угла определяют по изме-

Рис. 28. Измерение дирекционого угла хордоугломером

ренному углу в зависимости от четверти, в которой расположен ориентир. Зависимость между измеренным углом а’ и дирекционным углом а показана на рис. 29.

Углы хордоугломером можно измерить си средней ошибкой 0-01—0-02 дел. угл. (4— 8′).

Рис. 29. Переход от угла а’, измеренного хордоугломером, к дирекционному углу а

Измерение артиллерийским кругом. Центр круга совмещают с исходным пунктом (главной точкой условного знака) и круг устанавливают так, чтобы диаметр его 0—30 был параллелен вертикальным линиям координатной сетки, а нуль направлен на север. Затем масштабную линейку совмещают с главной точкой условного знака ориентира и на пересечении ребра линейки со шкалой круга считывают величину угла.

Артиллерийским кругом можно измерить дирекционный угол и без масштабной линейки (рис. 30). В этом случае предварительно прочерчивают на карте линию через главные точки условных знаков исходного пункта и ориентира. Затем артиллерийский круг устанавливают, как указано выше, и против прочерченной линии считывают по шкале круга величину дирекционного угла.

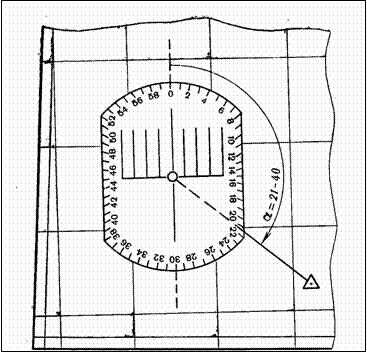
Рис. 30. Измерение дирекционного угла артиллерийским кругом

Артиллерийским кругом дирекционный угол. можно измерить со средней ошибкой 0-03 дел. угл.

При отделочных работах и строительстве бывает нужна четкая геометрия: перпендикулярные стены и иные конструкции, требующие прямого угла в 90 градусов. Обыкновенный угольник не может позволить проверить или разметить углы со сторонами в несколько метров. Описываемый же метод превосходно подходит для разметки или проверки любых углов — длинна сторон не ограничена. Основной инструмент для измерений — рулетка.

Мы будем рассматривать точную разметку прямого угла, а также метод проверки уже размеченных углов на стенах и других объектах.

Теорема Пифагора

Теорема основана на утверждении, что у прямоугольного треугольника сумма квадратов длин катетов равна квадрату длины гипотенузы. В виде формулы записывается это так:

Стороны a и b — катеты, между которыми угол равен ровно 90 градусов. Следовательно, сторона c — гипотенуза. Подставляя в эту формулу две известные величины, мы можем вычислить третью, неизвестную. А следовательно можем размечать прямые углы, а также проверять их.

Теорема Пифагора известна еще под названием «египетский треугольник». Это треугольник со сторонами 3, 4 и 5, причем совершенно не важно, в каких единицах длинны. Между сторонами 3 и 4 — ровно девяносто градусов. Проверим данное утверждение вышеприведенной формулой: a²+b²=c² = (3×3)+(4×4) = 9+16 = (5×5) = 25 — все сходится!

А теперь применим теорему на практике.

Проверка прямого угла

Начнем с самого простого — проверки прямого угла с помощью теоремы Пифагора. Самым частым примером в отделке и строительстве является проверка перпендикулярности стен. Перпендикулярные стены — это стены, расположенные друг к другу под прямым углом 90°.

Итак, берем любой проверяемый внутренний угол. На стенах (на одной высоте) или на полу отмечаем на обоих стенах отрезки произвольных длин. Длинна этих отрезков произвольная, по возможности нужно отмечать как можно больше, но чтобы между отметками на стенах удобно было мерить диагональ. Например, мы отметили 2,5 метра (или 250 см.) на одной стене и 3 метра (или 300 см.) на другой. Теперь длину отрезка каждой стены возводим в квадрат (умножаем саму на себя) и получившиеся произведения складываем. Выглядит это так: (2,5×2,5)+(3×3)=15,25 — это диагональ в квадрате. Теперь нужно извлечь из этого числа квадратный корень √15,25≈3,90 — 3,9 метра должна составлять диагональ между нашими отметками. Если измерение рулеткой показывает другую длину диагонали — проверяемый угол развернут и имеет отклонение от 90°.

Калькулятор расчета диагонали прямого угла

Извлечение квадратного корня никогда меня не привлекало — простому человеку не обойтись без калькулятора, к тому же, не на всех мобильных устройствах калькуляторы умеют извлекать его. Поэтому можно пользоваться упрощенным методом. Нужно лишь запомнить: у прямого угла со сторонами ровно 100 сантиметров, диагональ равна 141,4 см. Таким образом, у прямого угла со сторонами 2 м. — диагональ равна 282,8 см. То есть на каждый метр плоскости приходится 141,4 см. У этого метода один недостаток: от измеряемого угла нужно откладывать одинаковые расстояния на обеих стенах и отрезки эти должны быть кратны метру. Не буду утверждать, но по моей скромной практике — это гораздо удобнее. Хотя не стоит забывать о первоначальном способе совсем — в некоторых случаях он очень актуален.

Сразу же возникает вопрос: какое отклонение от вычисленной длинны диагонали считать нормой (погрешностью), а какое нет? Если проверяемый угол с отмеченными сторонами по 1 м. будет 89°, то диагональ уменьшится до 140 см. Из понимания этой зависимости можно сделать объективный вывод, что погрешность диагонали 141,4 см. в несколько миллиметров не даст отклонения в один целый градус.

Как проверить внешний угол? Проверка внешнего угла по сути не отличается, нужно лишь продлить линии каждой стены на полу (или земле, при помощи шнура) и получившийся внутренний угол измерить обычным способом.

Как разметить прямой угол рулеткой

Разметка может основываться как на общей теореме Пифагора, так и на принципе «египетского треугольника». Однако это только в теории линии просто чертятся на бумаге, «ловить» же все выбранные размеры растянутыми шнурами или линиями на полу — задача посложнее.

Поэтому я предлагаю упрощенный способ, основанный на диагонали 141,4 см. у треугольника со сторонами 100 см. Вся последовательность разметки изображена на картинках ниже. Важно не забывать: диагональ 141,4 см. нужно умножать на количество метров в отрезке А-Б. Отрезки А-Б и А-В должны быть равны и соответствовать целому числу в метрах. Картинки увеличиваются по клику!

Как разметить острый угол

Гораздо реже возникает надобность в создании острых углов, в частности 45°. Для формирования подобных фигур формулы более сложные, однако это не самое проблематичное. Гораздо сложнее свести все линии, начерченные или натянутые шнурами — дело это непростое. Поэтому я предлагаю использовать упрощенный метод. Сначала размечается прямой угол 90°, а затем диагональ 141,4 делится на нужное количество равных частей. Например, чтобы получить 45°, диагональ нужно поделить пополам и от точки А провести линию через место деления. Таким образом мы получим два угла по 45 градусов. Если поделить диагональ на 3 части, то получится три угла по 30 градусов. Думаю алгоритм вам понятен.

Собственно я рассказал все, что мог рассказать, надеюсь все изложил понятным языком и у вас больше не возникнет вопросов как размечать и проверять прямые углы. Стоит добавить, что уметь делать это должен любой отделочник или строитель, ведь полагаться на строительный угольник небольшого размера — непрофессионально.

С измерением длины, ширины и высоты домашнему мастеру приходится сталкиваться постоянно. Угол в 90° или 45° тоже не редко приходится выдерживать. Иначе качественно ремонт квартиры или изготовление самоделок не выполнить. Точности при выполнении линейных измерений 1 мм в подавляющем большинстве случаев достаточно, и для них подойдет рулетка или простая линейка.

Зачастую рулетки имеют дополнительно пузырьковый уровень, который позволяет выставить горизонтально мебель, холодильник и другие предметы. Но точность такого уровня не высокая из-за маленькой длины опорной плоскости рулетки. В дополнение колбочка с пузырьком воздуха в рулетках часто установлена не точно, что не обеспечивает горизонтальность и выполненной работы.

В продаже, для измерения линейных размеров представлен широкий ряд лазерных измерительных приборов, но, к сожалению, из-за высокой цены они не доступны для непрофессионалов.

Инструкция
по применению штангенциркуля (колумбуса)

Штангенциркуль – это линейный измерительный инструмент служащий для измерения наружных и внутренних размеров деталей включая глубину, с точностью 0,1 мм.

Измерить диаметр сверла, самореза и размеры других небольших деталей с достаточной точностью линейкой не получится. В таких случаях нужно использовать штангенциркуль, который позволяет измерять линейные размеры с точностью до 0,1 мм. С помощью штангенциркуля можно выполнить измерение толщины листового материала, внутреннего и внешнего диаметров трубы, диаметр высверленного отверстия, его глубину и другие измерения.

Штангенциркули бывают с отсчетом измеряемой величины по линейке и нониусу, циферблату часового типа и цифровому индикатору. Разновидность штангенциркуля с линейкой для измерения глубины отверстий профессионалы еще называют «Колумбус».

Доступным по цене, высоконадежным является штангенциркуль с нониусом типа ШЦ-1 с диапазоном измерений от 0 до 125 мм, что для большинства случаев вполне достаточно. Штангенциркуль ШЦ-1 дополнительно позволяет измерять диаметр отверстий и глубину.

В настоящее время в продаже появился цифровой пластиковый штангенциркуль китайского производства ценой менее $4, фотография которого представлена ниже.

Штангенциркуль из пластмассы, хотя его губки сделаны из карбона, назвать измерительным инструментом сложно, так как он не сертифицирован и поэтому точность показаний 0,1 мм заявленная производителем не гарантирована. В дополнение при частом использовании пластик быстро износится, и погрешность показаний увеличится.

Штангенциркуль из пластмассы, если его показания точны для домашних редких измерений вполне подойдет. Для проверки штангенциркуля можно измерять хвостовик сверла, на котором выбит размер или диаметр штыря электрической вилки.

Устройство и принцип работы нониуса штангенциркуля

Устроен классический штангенциркуль следующим образом. На измерительной штанге с помощью пазов установлена подвижная рамка. Для того, чтобы рамка плотно сидела, внутри установлена плоская пружина и предусмотрен винт, для жесткой ее фиксации. Фиксация необходима при проведении разметочных работ.

На штанге нанесена метрическая шкала с шагом 1 мм и цифрами обозначены сантиметровые деления. На рамке нанесена дополнительная шкала с 10 делениями, но с шагом 1,9 мм. Шкала на рамке называется нониусом в честь ее изобретателя португальского математика П.Нуниша. Штанга и рамка имеют измерительные губки для наружных и внутренних измерений. К рамке дополнительно закреплена линейка глубиномера.

Измерения выполняются зажимом между губками детали. После зажима рамка фиксируется винтом для того, чтобы она не сместилась. Количество миллиметров отсчитывается по шкале на штанге до первой риски нониуса. Десятые доли миллиметров отсчитываются по нониусу. Какой штрих по счету слева на право на нониусе совпадет с любой из рисок шкалы на штанге, столько и будет десятых долей миллиметра.

Как видно на фото, измеренный размер составляет 3,5 мм, так как от нулевой отметки шкалы на штанге до первой риски нониуса получилось 3 полных деления (3 мм) и на нониусе совпала с риской шкалы штанги риска пятого деления нониуса (одно деление на нониусе соответствует 0,1 мм измерений).

Примеры измерения штангенциркулем

Для измерения толщины или диаметра детали нужно развести губки штангенциркуля, вставить в них деталь и свести губки до соприкосновения с поверхностью детали. Надо проследить, чтобы плоскости губок при смыкании были параллельны плоскости измеряемой детали. Внешний диаметр трубы измеряется точно так же, как и размер плоской детали, только нужно, чтобы губки прикасались к диаметрально противоположным сторонам трубы.

Для того, чтобы измерять внутренний размер в детали или внутренний диаметр трубы, у штангенциркуля есть дополнительные губки для внутренних измерений. Их заводят в отверстие и раздвигают до упора в стенки детали. При измерении внутренних диаметров отверстий добиваются максимального показания, а при измерении в отверстии параллельных сторон, добиваются минимальных показаний.

В некоторых типах штангенциркулей губки не смыкаются до нуля и имеют собственную толщину, которая обычно на них выбита, например, число «10», хотя первая риска нониуса стоит на нулевой отметке. В случае измерения внутренних отверстий таким штангенциркулем к считанным показаниям по шкале нониуса добавляется 10 мм.

С помощью штангенциркуля типа колумбус, имеющего подвижную линейку глубиномера можно измерять глубину отверстий в деталях.

Для этого нужно полностью выдвинуть линейку глубиномера из штанги, вставить ее до упора в отверстие. Подвести до упора в поверхность детали торца штанги штангенциркуля, при этом не допуская выхода линейки глубиномера из отверстия.

На фотографии, для наглядности, я продемонстрировал измерение глубины отверстия, приложив линейку глубиномера штангенциркуля с внешней стороны отрезка трубы.

Примеры выполнения разметки деталей штангенциркулем

Штангенциркуль не предназначен для нанесения разметочных линий на материалах и деталях. Но если губки штангенциркуля для наружных измерений заточить на мелкозернистом наждачном круге, придав им острую форму, как показано на фотографии, то разметку штангенциркулем производить будет довольно удобно.

Снимать лишний металл с губок нужно очень аккуратно и медленно, не допуская цветов побежалости металла губок от сильного разогрева, иначе можно их испортить. Чтобы ускорить работу, для охлаждения губок, можно периодически окунать их на непродолжительное время в емкость с холодной водой.

Для того, чтобы отмерять полоску листового материала с параллельными сторонами, нужно раздвинуть губки штангенциркуля ориентируясь по шкале на заданный размер, одной губкой вести по торцу листа, а второй процарапать линию. Так как губки штангенциркуля закалены, они не истираются. Можно размечать как мягкие материалы, так и твердые (медь, латунь, сталь). Остаются хорошо видные риски.

С помощью заточенных остро губок штангенциркуля можно легко наметить линию окружности. Для этого в центре делается неглубокое отверстие диаметром около 1 мм, в него упираясь одной из губок, второй прочерчивают линию окружности.

Благодаря доработке формы губок штангенциркуля для наружных измерений, появилась возможность точно, удобно и быстро выполнять разметку деталей для их последующей механической обработки.

Как измерять микрометром на практике

Получить размер изделий с точностью 0,01 мм можно выполнив измерения микрометром. Их много модификаций, но самый распространенный это гладкий микрометр типа МК-25, обеспечивающий диапазон измерений от 0 до 25 мм с точностью 0,01 мм. Микрометром удобно измерять диаметр сверла, толщину листового материала, диаметр провода.

Микрометр представляет собой скобу, с одной стороны которой находится опорная пятка, а с другой имеется стебель и высокоточная резьба, в которую закручивается микровинт. На стебле нанесена метрическая шкала, по которой выполняется отсчет миллиметров. На микровинте имеется вторая шкала с 50 делениями, по которой отсчитываются сотые доли мм. Сумма этих двух величин является измеренным размером.

Для того, чтобы выполнить измерение микрометром, деталь размещают между пяткой и торцом микрометрического винта и вращают по часовой стрелке за ручку трещотки (находится на торце барабана микрометрического винта) до тех пор, пока трещотка не издаст три щелчка.

На стебле нанесено две шкалы с шагом 1 мм – основная оцифрованная через каждых 5 мм и дополнительная, сдвинутая относительно основной на 0,5 мм. Наличие двух шкал позволяет повысить тонность измерений.

Отсчет показаний выполняется следующим образом. Сначала считывают, сколько целых, не закрытых барабаном, миллиметров получилось по оцифрованной, нижней шкале на стебле. Далее проверяют по верхней шкале наличие риски, расположенной правее от риски нижней шкалы. Если риски не видно, то переходят к снятию показаний со шкалы на барабане. Если риска просматривается, значит, к целому числу полученных миллиметров добавляется еще 0,5 мм. Показания на барабане отсчитывают относительно прямой линии, нанесенной вдоль стебля между шкалами.

Например, размер измеренной детали составляет: 13 мм по нижней шкале, на верхней шкале открытой метки, правее открытой на нижней шкале нет, значить 0,5 мм добавлять не нужно, плюс 0,23 мм по шкале барабана, в результате сложения получаем: 13 мм+0 мм+0,23 мм=13,23 мм.

Микрометр с цифровым отсчетом результатов измерений применять удобнее и позволяет измерять с точностью до 0,001 мм.

Если, например, села батарейка, то цифровым микрометром можно выполнять измерения точно так же, как и гладким МК-25, так как имеется и система отсчета по делениям с точностью 0,01 мм. Цена микрометров с цифровым отсчетом результатов измерений высока и для домашнего мастера неподъемна.

Как измерять трубу большого диаметра

Губки штангенциркуля с диапазоном измерений от 0 до 125 мм имеют длину 40 мм и поэтому позволяют измерять трубы с внешним диаметром до 80 мм. В случае необходимости измерять трубу большего диаметра или при отсутствии под рукой штангенциркуля можно воспользоваться народным способом. Обвить трубу по окружности одним витком не растягивающейся нитки или проволоки, измерять длину этого витка с помощью простой линейки, а затем разделить полученный результат на число Π=3,14.

Онлайн калькулятор для расчета диаметра трубы по ее окружности
Суммарная длина намотки, мм:
Количество витков:

Не смотря на простоту, такой способ измерения диаметра трубы позволяет обеспечить точность 0,5 мм, что для домашнего мастера вполне достаточно. Для более точного измерения нужно намотать больше витков.

Как измерять угол

Для получения заданного угла при разметке можно воспользоваться транспортиром, с которым все познакомились еще в школе на уроках геометрии. Для измерения в быту точности его вполне достаточно.

На фотографии представлена пластмассовая линейка в виде треугольника, имеющего углы 45º и 90º, с встроенным транспортиром. С помощью него можно выполнить разметку и проверить точность полученного угла.

При выполнении разметки металлических деталей используют слесарный металлический угольник, обеспечивающие более высокую точность измерений.

Как пользоваться стуслом

Для получения прямого или угла 45º без разметки, удобно использовать приспособление, которое называется стусло. С помощью стусла удобно пилить в размер под углом наличники для дверей, багет, плинтуса и многое другое. Распил получается с требуемым углом автоматически.

Достаточно отмерять длину, вложить полоску материала между вертикальными стенками стусла и удерживая рукой выполнить распил. Для получения качественного торца доски следует использовать пилу с мелкими зубцами. Хорошо подходит ножовка по металлу. Удается распиливать даже лакированные доски без сколов лака.

Угол 45 0 при пилении с использования стусла, получается также легко, как и прямой. Благодаря высоким направляющим стенок стусла можно распиливать доски разной толщины.

Стусло можно купить готовое, но его не сложно сделать самостоятельно из подручного материала. Достаточно взять три доски из дерева или фанеры подходящего размера, и к боковым торцам одной из них саморезами прикрутить две другие. Сделать направляющие пропилы под требуемыми углами и приспособление стусло готово.

определение угла, измерение углов, обозначения и примеры

Угол – основная геометрическая фигура, которую разберем на протяжение всей темы. Определения, способы задания, обозначения и измерения угла. Разберем принципы выделения углов на чертежах. Вся теория проиллюстрирована и имеет большое количество наглядных чертежей.

Определение угла

Определение 1

Угол – простая важная фигура в геометрии. Угол напрямую зависит от определения луча, который в свою очередь состоит из базовых понятий точки, прямой и плоскости. Для досконального изучения необходимо углубиться по темам прямая на плоскости – необходимые сведения и плоскость – необходимые сведения.

Понятие угла начинается с понятий о точке, плоскости и прямой, изображенной на этой плоскости.

Определение 2

Дана прямая a на плоскости. На ней обозначим некоторую точку O. Прямая разделена точкой на две части, каждая из которых имеет название луч, а точка O – начало луча.

Иначе говоря, луч или полупрямая – это часть прямой, состоящая из точек заданной прямой, расположенных на одной стороне относительно начальной точки, то есть точки O.

Обозначение луча допустимо в двух вариациях: одной строчной или двумя прописными буквами латинского алфавита. При обозначении двумя буквами луч имеет название, состоящее из двух букв. Рассмотрим подробнее на чертеже.

Перейдем к понятию определения угла.

Определение 3

Угол – это фигура, расположенная в заданной плоскости, образованная двумя несовпадающими лучами, имеющими общее начало. Сторона угла является лучом, вершина – общее начало сторон.

Имеет место случай, когда стороны угла могут выступать в роли прямой линии.

Определение 4

Когда обе стороны угла расположены на одной прямой или его стороны служат как дополнительные полупрямые одной прямой, то такой угол называют развернутым.

На рисунке ниже изображен развернутый угол.

Точка на прямой

Чем измерить угол 🚩 вымерять треугольник 🚩 Школы

Самый широко известный и простой в использовании инструмент для измерения углов — транспортир. Для того, чтобы с помощью него измерить плоский угол, необходимо совместить центральное отверстие транспортира с вершиной угла, а нулевое деление — с одной из его сторон. Значение деления, которое пересечет вторая сторона угла и будет величиной угла. Таким образом можно измерить углы до 180 градусов. Если же необходимо измерить угол величиной свыше 180 градусов, достаточно измерить угол, образуемый его сторонами и вершиной и дополняющий его до 360 градусов (полного угла), а затем вычесть измеренную величину из 360 градусов. Полученная величина и будет величиной искомого угла.
Для измерения величины плоского угла достаточно дополнить угол еще одной стороной так, чтобы образовался прямоугольный треугольник. Измерив величины сторон полученного треугольника, можно получить значение любой тригонометрической функции угла, величину которого необходимо узнать. Зная значение синуса, косинуса, тангенса или котангенса угла, можно, воспользовавшись таблицей Брадиса, узнать величину угла.
Есть определенные известные величины углов, которые можно измерить с помощью школьной линейки-угольника. Выпускают два вида таких линеек, оба вида представляют из себя прямоугольные треугольники, выполненные из дерева, пластика или металла. Первый вид угольника — равнобедренный прямоугольный треугольник, два угла которого имеют величину 45 градусов. Второй вид — прямоугольный треугольник, один из углов которого равен 30 градусам, а второй — 60 градусам соответственно. Совместив одну из вершин угольника с вершиной угла и сторону — со стороной угла при совпадении другой стороны угла со смежной стороной угольника можно найти соответствующую величину угла. Таким образом, с помощью линеек-угольников можно найти величины углов в 30, 45, 60 и 90 градусов.
Инструменты, перечисленные в предыдущих пунктах, используются для измерения углов на плоскости. На практике — в геодезии, строительстве, топографии — используется специальный прибор для измерения так называемых горизонтальных и вертикальных углов под названием теодолит. Основными измерительными элементами теодолита являются специальные цилиндрические кольца (лимбы), на которые равномерно нанесена градусная разметка. Установленный с помощью специальной подставки в вершину угла прибор наводится с помощью зрительной трубы сначала на точку, находящуюся на одной стороне угла, где производится замер, затем на другой стороне угла, и снова производится замер. Разность замеров определяет величину угла в первом полуприеме. Затем производится второй полуприем — в обратном направлении. Среднее арифметическое значений, полученных в двух полуприемах является величиной измеряемого угла.

Угол. Измерение угла — урок. Математика, 5 класс.

Геометрическая фигура угол образуется из двух лучей с общей начальной точкой.

Общая точка называется вершиной угла, а лучи — сторонами угла.

Если угол образован дополнительными (или противоположными) лучами, то он называется развёрнутым.

 

Для названия угла часто используют три большие латинские буквы, название вершины угла пишется посередине.

Иногда угол можно назвать только одной буквой, которая находится у вершины.

Можно также познакомиться с греческим алфавитом и использовать маленькие буквы для названий углов.

Чаще используют: α,β,γ,δ,ϵ,η,ϕ,ω — и другие.

 

Попытаемся представить точку как что-то бесконечно маленькое, а прямую — как что-то бесконечно простирающееся в обе стороны.

 

 

Пример:

описание рисункa:

1. на рисунке показан угол ∡ABC, ∡B или ∡α;

2. также нарисован развёрнутый угол ∡KLM.

Так же как каждый отрезок имеет длину, которую можно измерить линейкой и выразить в единицах измерения, так и каждый угол имеет величину.

 

За единицу измерения углов принимают градус, что является 1180 частью развёрнутого угла.

Величина развёрнутого угла — \(180°\).

Углы измеряют транспортиром.

 

 

Особый угол, половина развёрнутого угла — прямой угол.

Прямой угол обозначают маленьким квадратиком внутри угла.

Величина прямого угла равна \(90°\).

 

Углы, величина которых меньше \(90°\), называются острыми.

 

Углы, величина которых больше \(90°\), называются тупыми.

Что такое транспортир? Правила измерения углов

Каждый школьник знает, что такое транспортир. Этот, казалось бы, неприглядный инструмент выполняет очень важные функции не только на уроках математики. О том,что он собой представляет, а также как правильно им пользоваться, расскажем далее.

Что такое транспортир?

Транспортиром называют предмет, с помощью которого каждый из нас может не только измерять углы, но и строить их. Внешне он напоминает полукруглую линейку со шкалой и делениями. Внизу, на ровной поверхности, расположена привычная нам прямая линейка для измерения отрезков. В верхней части — полукруг с двойной шкалой для измерений. В каждом из направлений шкала рассредоточена по транспортиру от 0 до 180 градусов.

Правила пользования

В школе объясняют, что такое транспортир, на уроках математики. Именно здесь есть необходимость в измерениях.

Для того чтобы нам узнать, чему равен один градус, нужно окружность поделить на 360 равных частей. Одна из таких частей и будет равна 1 градусу. Величина окружности никак не повлияет на градус! Это легко проверить.

Нарисуем две окружности разного диаметра и поделим каждую на 360 равных частей. Затем наложим меньшую окружность на большую и увидим, что линии совпали.

Измеряем угол

Транспортир помогает построить и измерить угол. Градус — это общепринятая единица, которой пользуются для измерения углов. Встречается несколько разновидностей углов:

• Острый. Таким называют угол до 90 градусов.
• Прямым является угол, равный 90 градусам.
• Тупой угол варьируется в диапазоне от 90 до 180 градусов.
• Развёрнутый угол представляет собой прямую линию или 180 градусов.
• Полный угол выглядит как окружность и составляет 360 градусов.

Нетрудно разобраться, как измерить угол. Для того чтобы узнать, какова величина угла, нам необходимо установить транспортир таким образом, чтобы его центр располагался в вершине угла, а прямая сторона совпала с одной из его сторон. Шкала укажет нам количество градусов данного угла. Вот таким нехитрым способом мы можем узнать, что за угол перед нами.

Для построения угла с заданным градусом следует приложить прямую часть транспортира к линии, а его центр — к началу линии. Впоследствии эта точка будет являться вершиной угла. Затем на шкале отыскиваем заданное число и ставим точку. Теперь транспортир можно снять и соединить отрезком начало линии (вершину угла) с отмеченной точкой.

Школьные канцтовары, произведенные разными компаниями, отличаются по материалу, цвету, размеру. Так вот: тем, у кого транспортир оказался больше длины угла, и не представляется возможным определить его величину, сторону угла необходимо продлить, используя прямую линейку.

Набор школьника

Неспроста учащиеся младшего звена не знакомы с транспортиром. При его применении должна быть заложена некая база знаний. Для полноценной работы с ним на уроке ребята изучают ряд сопутствующих предметов. Прежде чем узнать, что такое транспортир, школьники должны в совершенстве овладеть прямой линейкой, чертить ровные линии, изучить сложение и вычитание, освоить циркуль, знать геометрические фигуры и так далее. Весь этот процесс занимает время, и только окончив начальную школу, ученик может добавить транспортир в свой набор инструментов.

Ученикам сейчас предлагаются школьные канцтовары в огромном выборе. Транспортир не исключение. Производители стараются угодить самым требовательным запросам покупателей. Инструменты изготавливают в различной цветовой гамме. Яркие цвета всегда нравятся детям. Порой даже в одном классе не сыскать одинаковых транспортиров, что облегчает при утрате их поиск. Формы и размеры каждый выбирает на свой вкус.

Большинство таких товаров выпускают из пластмассы, и это значительно уменьшает его стоимость. Но есть деревянные и даже железные транспортиры. Как показывает практика, металлические хоть и непрозрачны, но практичнее в том плане, что шкала не стирается, а это позволяет гораздо дольше применять его в действии, с точностью определяя углы.

Транспортир не так востребован школьниками, как линейка, но он сопровождает учеников вплоть до выпускного экзамена. Некоторые из выпускников школы выбирают специальности, которые связаны с измерением и построением углов, проектированием зданий и сооружений, работой с чертежами. В силу своих профессий им постоянно приходится сталкиваться с транспортирами и его производными. Но и бывшие одноклассники нынешних инженеров, порой даже с глубочайшим гуманитарным уклоном, без труда вспомнят навыки обращения с этим предметом и определят количество градусов у любого угла.

Итог

Сегодня современные дети привыкли добывать любую информацию из интернета. Однако он никак не поможет в измерении углов. Лишь только умение пользоваться транспортиром даст возможность правильно их определять. Будущим инженерам и проектировщикам это бесспорно пригодится в работе, да и каждый образованный человек должен обладать навыками работы с транспортирами, поэтому уметь пользоваться таким инструментом должен каждый!