Геометрия внутренний угол — kak.ufolabs.ru
Данные геометрические фигуры окружают нас повсюду. Выпуклые многоугольники бывают природными, например, пчелиные соты или искусственными (созданными человеком). Эти фигуры используются в производстве различных видов покрытий, в живописи, архитектуре, украшениях и т.д. Выпуклые многоугольники обладают тем свойством, что все их точки располагаются по одну сторону от прямой, что проходит через пару соседних вершин этой геометрической фигуры. Существуют и другие определения. Выпуклым называется тот многоугольник, который расположен в единой полуплоскости относительно любой прямой, содержащей одну из его сторон.
Содержание статьи:
Выпуклые многоугольники
 В курсе элементарной геометрии всегда рассматриваются исключительно простые многоугольники. Чтобы понять все свойства таких геометрических фигур необходимо разобраться с их природой. Для начала следует уяснить, что замкнутой называется любая линия, концы которой совпадают. Причем фигура, образованная ею, может иметь самые разные конфигурации. Многоугольником называют простую замкнутую ломаную линию, у которой соседние звенья не располагаются на одной прямой. Ее звенья и вершины являются, соответственно, сторонами и вершинами этой геометрической фигуры. Простая ломаная не должна иметь самопересечений.
В курсе элементарной геометрии всегда рассматриваются исключительно простые многоугольники. Чтобы понять все свойства таких геометрических фигур необходимо разобраться с их природой. Для начала следует уяснить, что замкнутой называется любая линия, концы которой совпадают. Причем фигура, образованная ею, может иметь самые разные конфигурации. Многоугольником называют простую замкнутую ломаную линию, у которой соседние звенья не располагаются на одной прямой. Ее звенья и вершины являются, соответственно, сторонами и вершинами этой геометрической фигуры. Простая ломаная не должна иметь самопересечений.
Вершины многоугольника называют соседними, в том случае если они представляют собой концы одной из его сторон. Геометрическая фигура, у которой имеется n-е число вершин, а значит, и n-е количество сторон, называется n-угольником. Саму ломаную линию называют границей или контуром этой геометрической фигуры. Многоугольной плоскостью или плоским многоугольником называют конечную часть любой плоскости, им ограниченной. Соседними сторонами этой геометрической фигуры называют отрезки ломаной линии, исходящие из одной вершины. Они будут не соседними, если исходят их разных вершин многоугольника.
Другие определения выпуклых многоугольников
 В элементарной геометрии существует еще несколько эквивалентных по своему значению определений, указывающих на то, какой многоугольник называется выпуклым. Причем все эти формулировки в одинаковой степени верны. Выпуклым считается тот многоугольник, у которого:
В элементарной геометрии существует еще несколько эквивалентных по своему значению определений, указывающих на то, какой многоугольник называется выпуклым. Причем все эти формулировки в одинаковой степени верны. Выпуклым считается тот многоугольник, у которого:
• каждый отрезок, что соединяет две любые точки внутри него, полностью лежит в нем;
• внутри него лежат все его диагонали;
• любой внутренний угол не превышает 180°.
Многоугольник всегда разбивает плоскость на 2 части. Одна из них – ограниченная (она может быть заключена в круг), а другая — неограниченная. Первую называют внутренней областью, а вторую – внешней областью этой геометрической фигуры. Данный многоугольник является пересечением (иными словами — общей составляющей) нескольких полуплоскостей. При этом каждый отрезок, имеющий концы в точках, которые принадлежат многоугольнику, полностью принадлежит ему.
Разновидности выпуклых многоугольников
Определение выпуклого многоугольника не указывает на то, что их существует множество видов. Причем у каждого из них имеются определенные критерии. Так, выпуклые многоугольники, у которых есть внутренний угол равный 180°, называются слабовыпуклыми. Выпуклая геометрическая фигура, что имеет три вершины, называется треугольником, четыре — четырехугольником, пять — пятиугольником и т. д. Каждый из выпуклых n-угольников отвечает следующему важнейшему требованию: n должно равняться или быть больше 3. Каждый из треугольников является выпуклым. Геометрическая фигура данного типа, у которой все вершины располагаются на одной окружности, называется вписанной в окружность. Выпуклый многоугольник называют описанным, если все его стороны около окружности прикасаются к ней. Два многоугольника называют равными только в том случае, когда при помощи наложения их можно совместить. Плоским многоугольником называют многоугольную плоскость (часть плоскости), что ограничена этой геометрической фигурой.
Правильные выпуклые многоугольники
Правильными многоугольниками называют геометрические фигуры с равными углами и сторонами. Внутри них имеется точка 0, которая находится на одинаковом расстоянии от каждой из его вершин. Ее называют центром этой геометрической фигуры. Отрезки, соединяющие центр с вершинами этой геометрической фигуры называют апофемами, а те, что соединяют точку 0 со сторонами – радиусами.
Правильный четырехугольник – квадрат. Правильный треугольник называют равносторонним. Для таких фигур существует следующее правило: каждый угол выпуклого многоугольника равен 180° * (n-2)/ n,
где n – число вершин этой выпуклой геометрической фигуры.
Площадь любого правильного многоугольника определяют по формуле:
S = р * h,
где p равно половине суммы всех сторон данного многоугольника, а h равно длине апофемы.
Свойства выпуклых многоугольников
Выпуклые многоугольники имеют определенные свойства. Так, отрезок, который соединяет любые 2 точки такой геометрической фигуры, обязательно располагается в ней. Доказательство:
Предположим, что Р – данный выпуклый многоугольник. Берем 2 произвольные точки, например, А, В , которые принадлежат Р. По существующему определению выпуклого многоугольника эти точки расположены в одной стороне от прямой, что содержит любую сторону Р. Следовательно, АВ также имеет это свойство и содержится в Р. Выпуклый многоугольник всегда возможно разбить на несколько треугольников абсолютно всеми диагоналями, которые проведены из одной его вершины.
Углы выпуклых геометрических фигур
Углы выпуклого многоугольника – это углы, что образованы его сторонами. Внутренние углы находятся во внутренней области данной геометрической фигуры. Угол, что образован его сторонами, которые сходятся в одной вершине, называют углом выпуклого многоугольника. Углы, смежные с внутренними углами данной геометрической фигуры, называют внешними. Каждый угол выпуклого многоугольника, расположенный внутри него, равен:
180° — х,
где х – величина внешнего угла. Эта простая формула действует в отношении любых геометрических фигур такого типа.
В общем случае, для внешних углов существует следующие правило: каждый угол выпуклого многоугольника равен разности между 180° и величиной внутреннего угла. Он может иметь значения в пределах от -180° до 180°. Следовательно, когда внутренний угол составляет 120°, внешний будет иметь величину в 60°.
Сумма углов выпуклых многоугольников
 Сумма внутренних углов выпуклого многоугольника устанавливается по формуле:
Сумма внутренних углов выпуклого многоугольника устанавливается по формуле:
180° * (n-2),
где n – число вершин n-угольника.
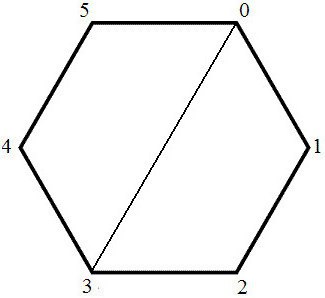
Сумма углов выпуклого многоугольника вычисляется довольно просто. Рассмотрим любую такую геометрическую фигуру. Для определения суммы углов внутри выпуклого многоугольника необходимо соединить одну из его вершин с другими вершинами. В результате такого действия получается (n-2) треугольника. Известно, что сумма углов любых треугольников всегда равна 180°. Поскольку их количество в любом многоугольнике равняется (n-2), сумма внутренних углов такой фигуры равняется 180° х (n-2).
Сумма углов выпуклого многоугольника, а именно любых двух внутренних и смежных с ними внешних углов, у данной выпуклой геометрической фигуры всегда будет равна 180°. Исходя из этого, можно определить сумму всех ее углов:
180 х n.
Сумма внутренних углов составляет 180° * (n-2). Исходя из этого, сумму всех внешних углов данной фигуры устанавливают по формуле:
180° * n-180°-(n-2)= 360°.
Сумма внешних углов любого выпуклого многоугольника всегда будет равна 360° (независимо от количества его сторон).
Внешний угол выпуклого многоугольника в общем случае представляется разностью между 180° и величиной внутреннего угла.
Другие свойства выпуклого многоугольника
Помимо основных свойств данных геометрических фигур, у них есть и другие, которые возникают при манипуляциях с ними. Так, любой из многоугольников может быть разделен на несколько выпуклых n-угольников. Для этого необходимо продолжить каждую из его сторон и разрезать эту геометрическую фигуру вдоль этих прямых линий. Разбить любой многоугольник на несколько выпуклых частей можно и таким образом, чтобы вершины каждого из кусков совпадали со всеми его вершинами. Из такой геометрической фигуры можно очень просто сделать треугольники путем проведения всех диагоналей из одной вершины. Таким образом, любой многоугольник, в конечном счете, можно разбить на определенное количество треугольников, что оказывается весьма полезным при решении различных задач, связанных с такими геометрическими фигурами.
Периметр выпуклого многоугольника
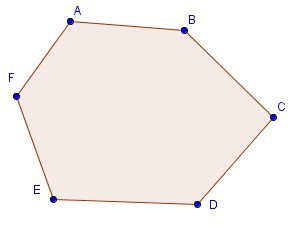
Отрезки ломаной линии, называемые сторонами многоугольника, чаще всего обозначаются следующими буквами: ab, bc, cd, de, ea. Это стороны геометрической фигуры с вершинами a, b, c, d, e. Сумма длины всех сторон этого выпуклого многоугольника называют его периметром.
Окружность многоугольника
Выпуклые многоугольники могут быть вписанными и описанными. Окружность, касающаяся всех сторон этой геометрической фигуры, называется вписанной в нее. Такой многоугольник называют описанным. Центр окружности, которая вписана в многоугольник, представляет собой точку пересечения биссектрис всех углов внутри данной геометрической фигуры. Площадь такого многоугольника равняется:
S = p * r,
где r – радиус вписанной окружности, а p – полупериметр данного многоугольника.
Окружность, содержащую вершины многоугольника, называют описанной около него. При этом данная выпуклая геометрическая фигура называется вписанной. Центр окружности, которая описана около такого многоугольника, представляет собой точку пересечения так называемых серединных перпендикуляров всех сторон.
Диагонали выпуклых геометрических фигур
Диагонали выпуклого многоугольника – это отрезки, которые соединяют не соседние вершины. Каждая из них лежит внутри этой геометрической фигуры. Число диагоналей такого n-угольника устанавливается по формуле:
N = n (n – 3)/ 2.
Число диагоналей выпуклого многоугольника играет важную роль в элементарной геометрии. Число треугольников (К), на которые возможно разбить каждый выпуклый многоугольник, вычисляется по следующей формуле:
К = n – 2.
Количество диагоналей выпуклого многоугольника всегда зависит от числа его вершин.
Разбиение выпуклого многоугольника
В некоторых случаях для решения геометрических задач необходимо разбить выпуклый многоугольник на несколько треугольников с непересекающимися диагоналями. Эту проблему можно решить путем выведения определенной формулы.
Определение задачи: назовем правильным некое разбиение выпуклого n-угольника на несколько треугольников диагоналями, пересекающимися только в вершинах этой геометрической фигуры.
Решение: Предположим, что Р1, Р2 , Р3 … , Pn – вершины этого n-угольника. Число Xn — количество его разбиений. Внимательно рассмотрим полученную диагональ геометрической фигуры Pi Pn. В любом из правильных разбиений Р1 Pn принадлежит определенному треугольнику Р1 Pi Pn, у которого 1<i<n. Исходя из этого и полагая, что і = 2,3,4 … , n-1, получается (n-2) группы этих разбиений, в которые включаются все возможные частные случаи.
Пусть і = 2 будет одной группой правильных разбиений, всегда содержащей диагональ Р2 Pn. Количество разбиений, которые входят в нее, совпадает с числом разбиений (n-1)-угольника Р2 Р3 Р4… Pn. Иными словами, оно равняется Xn-1.
Если і = 3, то эта другая группа разбиений будет всегда содержать диагонали Р3 Р1 и Р3 Pn. При этом количество правильных разбиений, что содержатся в данной группе, будет совпадать с числом разбиений (n-2)-угольника Р3 Р4… Pn. Другими словами, оно будет равняться Xn-2.
Пусть і = 4, тогда среди треугольников правильное разбиение непременно будет содержать треугольник Р1 Р4 Pn, к которому будет примыкать четырехугольник Р1 Р2 Р3 Р4, (n-3)-угольник Р4 Р5… Pn. Количество правильных разбиений такого четырехугольника равняется Х4, а число разбиений (n-3)-угольника равняется Xn-3. Исходя из всего изложенного, можно сказать, что полное количество правильных разбиений, которые содержатся в данной группе, равняется Xn-3 Х4. Другие группы, у которых і = 4, 5, 6, 7… будут содержать Xn-4 Х5, Xn-5 Х6, Xn-6 Х7 … правильных разбиений.
Пусть і = n-2, то количество правильных разбиений в данной группе будет совпадать с числом разбиений в группе, у которой i=2 (другими словами, равняется Xn-1).
Так как Х1 = Х2 = 0, Х3=1, Х4=2…, то число всех разбиений выпуклого многоугольника равно:
Xn = Xn-1 + Xn-2 + Xn-3 Х4 + Xn-4 Х5 + … + Х 5 Xn-4 + Х4 Xn-3 + Xn-2 + Xn-1.
Пример:
Х5 = Х4 + Х3 + Х4 = 5
Х6 = Х5 + Х4 + Х4 + Х5 = 14
Х7 = Х6 + Х5 + Х4 * Х4 + Х5 + Х6 = 42
Х8 = Х7 + Х6 + Х5 * Х4 + Х4 * Х5 + Х6 + Х7 = 132
Количество правильных разбиений, пересекающих внутри одну диагональ
При проверке частных случаев, можно прийти к предположению, что число диагоналей выпуклых n-угольников равняется произведению всех разбиений этой фигуры на (n-3).
Доказательство данного предположения: представим, что P1n = Xn * (n-3), тогда любой n-угольник возможно разбить на (n-2)-треугольников. При этом из них может быть сложен (n-3)-четырехугольник. Наряду с этим, у каждого четырехугольника будет диагональ. Поскольку в этой выпуклой геометрической фигуре могут быть проведены две диагонали, это значит, что и в любых (n-3)-четырехугольниках возможно провести дополнительные диагонали (n-3). Исходя из этого, можно сделать вывод, что в любом правильном разбиении имеется возможность провести (n-3)-диагонали, отвечающие условиям этой задачи.
Площадь выпуклых многоугольников
Нередко при решении различных задач элементарной геометрии появляется необходимость определить площадь выпуклого многоугольника. Предположим, что (Xi. Yi), i = 1,2,3… n представляет собой последовательность координат всех соседних вершин многоугольника, не имеющего самопересечений. В этом случае его площадь вычисляется по такой формуле:
S = ½ (∑ (Xi + Xi + 1) (Yi + Yi + 1)),
где (Х1, Y1) = (Xn +1, Yn + 1).
Источник: FB.ru
Читайте также
Геометрия. Урок 2. Углы — ЁП
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Угол – геометрическая фигура, образованная двумя лучами, выходящими из одной точки.
Стороны угла – лучи, которые образуют угол.
Вершина угла – точка, из которой выходят лучи.

Угол называют тремя заглавными латинскими буквами, которыми обозначены вершина и две точки, расположенные на сторонах угла.
Важно: в названии буква, обозначающая вершину угла, стоит между двумя буквами, обозначающими точки на сторонах угла. Так, угол, изображенный на рисунке, можно назвать: ∠AOB или ∠BOA, но ни в коем случае не ∠OAB,∠OBA,∠ABO,∠BAO.
Величину угла измеряют в градусах. ∠AOB=24°.

Биссектриса угла – это луч с началом в вершине угла, делящий его на два равных угла.
Или
Биссектриса угла – это геометрическое место точек, равноудаленных от сторон угла.

OD – биссектриса угла ∠AOB. Она делит этот угол на два равных угла.
∠AOD=∠BOD=∠AOB2
Точка D – произвольная точка на биссектрисе. Она равноудалена от сторон OA и OB угла ∠AOB.
Вертикальные углы – пара углов, у которых стороны одного угла являются продолжением сторон второго.
Свойство: вертикальные углы равны.
Смежные углы – пара углов, у которых одна сторона общая, а две другие стороны расположены на одной прямой.
Свойство: сумма смежных углов равна 180°.
Пример:

Пары углов
(1) и (3)
(2) и (4)
называются вертикальными.
По свойству вертикальных углов:
∠COD=∠AOB
∠BOD=∠AOC
Пары углов
(1) и (2)
(2) и (3)
(3) и (4)
(4) и (1)
называются смежными.
По свойству смежных углов:
∠COD+∠DOB=180°∠DOB+∠BOA=180°∠BOA+∠AOC=180°∠AOC+∠COD=180°
Прямая, пересекающая две заданные прямые, называется секущей этих прямых.

Существует пять видов углов, которые образуются при пересечении двух прямых секущей.
Пары углов:
(1) и (5)
(2) и (6)
(3) и (7)
(4) и (8)
называются соответственными.
(Легко запомнить: они соответствуют друг другу, похожи друг на друга).
Пары углов:
(3) и (5)
(4) и (6)
называются внутренними односторонними.
(Легко запомнить: лежат по одну сторону от секущей, между двумя прямыми).
Пары углов:
(1) и (7)
(2) и (8)
называются внешними односторонними.
(Легко запомнить: лежат по одну сторону от секущей по разные стороны от двух прямых).
Пары углов:
(3) и (6)
(4) и (5)
называются внутренними накрест лежащими.
(Легко запомнить: лежат между двумя прямыми, расположены наискосок друг относительно друга).
Пары углов:
(1) и (8)
(2) и (7)
называются внешними накрест лежащими.
(Легко запомнить: лежат по разные стороны от двух прямых, расположены наискосок друг относительно друга).
Если прямые, которые пересекает секущая, параллельны, то углы имеют следующие свойства:
- Соответственные углы равны.
- Внутренние накрест лежащие углы равны.
- Внешние накрест лежащие углы равны.
- Сумма внутренних односторонних углов равна 180°.
- Сумма внешних односторонних углов равна 180°.

Сумма углов произвольного n-угольника вычисляется по формуле:
Sn=180°⋅(n−2)
где n – это количество углов в n-угольнике.
Пользуясь этой формулой, можно вычислить сумму углов для произвольного n-угольника.
Сумма углов треугольника: S3=180°⋅(3−2)=180°
Сумма углов четырехугольника: S4=180°⋅(4−2)=360°
Сумма углов пятиугольника: S5=180°⋅(5−2)=540°
Так можно продолжать до бесконечности.
Правильный многоугольник – это выпуклый многоугольник, у которого все стороны равны и все углы равны.
На рисунках изображены примеры правильных многоугольников:
Чтобы найти величину угла правильного n-угольника, необходимо сумму углов этого многоугольника разделить на количество углов.
αn=180°⋅(n−2)n
Модуль геометрия: задания, связанные с углами
Скачать домашнее задание к уроку 2.
Угол / Начальные геометрические сведения / Справочник по геометрии 7-9 класс
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Начальные геометрические сведения
- Угол
Угол — геометрическая фигура
Мы знаем, что углом называется геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки.

Лучи — это стороны угла, а точка (их общее начало) — вершина угла
Изображать угол можно и так (не отмечаем точкой общее начало, считаем, что точка есть)

Обозначения угла
1)

На сторонах угла не отмечены точки (только обозначены большими латинскими буквами А и В)
Считается, что буква А обозначает любую точку на верхней стороне угла (по данному рисунку)
Точка В обозначает любую точку на нижней стороне угла (по данному рисунку)
Читаем: угол АОВ
Пишем:  АОВ
АОВ
2)
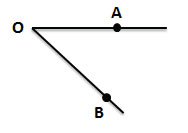
На сторонах угла отмечены и обозначены произвольные точки А и В
Читаем: угол АОВ
Пишем:  АОВ
АОВ
3)
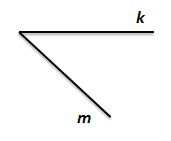
Стороны угла (лучи) обозначены малыми латинскими буквами k и m
Читаем: угол km
Пишем:  km
km
4)
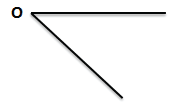
Обозначена только вершина угла
Читаем: угол О
Пишем: 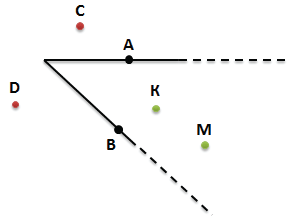 О
О
Развернутый угол
Построим прямую АВ и отметим на этой прямой точку О

Лучи ОА и ОВ лежат на одной прямой (являются дополнительными)
Угол АОВ называется развернутым

Угол на плоскости
Изобразим часть плоскости
(так как плоскость бесконечна, мы не можем изобразить ее всю, только часть ее)
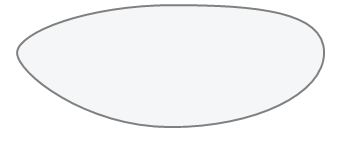
Построим на этой плоскости неразвернутый угол
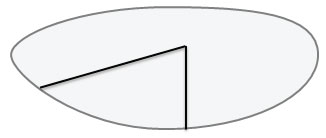
Этот угол делит плоскость на две части (области) — внешнюю и внутреннюю
Замечание
Любой угол разделяет плоскость на две части. Названия этих частей ( внутренняя область и внешняя область) применяется для неразвернутого угла.
Если угол развёрнутый, то любую из двух частей, на которые он разделяет плоскость, можно считать внутренней областью угла.
Расположение точек относительно угла
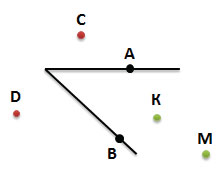
По рисунку определим положение отмеченных точек A, B, C, D, K, M
Точки А и В лежат на сторонах угла
Точки D и C лежат вне угла (во внешней области угла)
Точки К и М, лежат внутри угла (во внутренней области угла)
При необходимости мы можем продолжить стороны угла, например, чтобы уточнить положение точки М

Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Точки, прямые, отрезки
Провешивание прямой на местности
Луч
Равенство геометрических фигур
Сравнение отрезков
Сравнение углов
Длина отрезка
Единицы измерения длины, расстояний
Градусная мера угла
Измерение углов на местности
Смежные углы
Вертикальные углы
Перпендикулярные прямые
Построение прямых углов на местности
Начальные геометрические сведения
Правило встречается в следующих упражнениях:
7 класс
Задание 58, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 11, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 223, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 2, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 559, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 588, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 730, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 812, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 843, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 873, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
© budu5.com, 2020
Пользовательское соглашение
Copyright
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
Вписанные и центральные углы
Определение 1. Центральным угломназывают угол, вершина которого совпадает с центром окружности, а стороны являются радиусами радиусами (рис. 1).

Рис. 1
Определение 2. Вписанным углом называют угол, вершина которого лежит на окружности, а стороны являются хордами хордами (рис. 2).

Рис. 2
Напомним, что углы можно измерять в градусах и в радианах. Дуги окружности также можно измерять в градусах и в радианах, что вытекает из следующего определения.
Определение 3. Угловой мерой (угловой величиной) дуги окружности является величина центрального угла, опирающегося на эту дугу.
Теоремы о вписанных и центральных углах
| Фигура | Рисунок | Теорема |
| Вписанный угол |  | Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Посмотреть доказательство |
| Вписанный угол |  | Вписанные углы, опирающиеся на одну и ту же дугу равны. |
| Вписанный угол |  | Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды |
| Вписанный угол |  | Два вписанных угла, опирающихся на одну и ту же хорду, в сумме составляют 180°, если их вершины лежат по разные стороны от этой хорды |
| Вписанный угол |  | Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр |
| Окружность, описанная около прямоугольного треугольника |  | Середина гипотенузы прямоугольного треугольника является центром описанной Посмотреть доказательство |
| Вписанный угол |
Теорема: Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.
Посмотреть доказательство |
Теорема: Вписанные углы, опирающиеся на одну и ту же дугу равны.
|
Теорема: Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды
|
Теорема: Два вписанных угла, опирающихся на одну и ту же хорду, в сумме составляют 180°, если их вершины лежат по разные стороны от этой хорды
|
Теорема: Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр
|
| Окружность, описанная около прямоугольного треугольника |
Теорема: Середина гипотенузы прямоугольного треугольника является центром описанной
Посмотреть доказательство |
Теоремы об углах, образованных хордами, касательными и секущими
| Фигура | Рисунок | Теорема | Формула |
| Угол, образованный пересекающимися хордами |  | Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами. Посмотреть доказательство |  |
| Угол, образованный секущими, которые пересекаются вне круга | 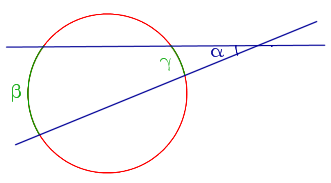 | Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами Посмотреть доказательство | 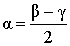 |
| Угол, образованный касательной и хордой, проходящей через точку касания |  | Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами Посмотреть доказательство | 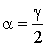 |
| Угол, образованный касательной и секущей | 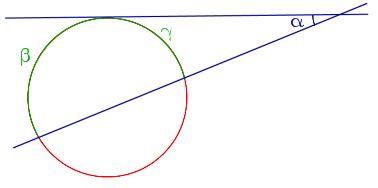 | Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами Посмотреть доказательство | 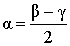 |
| Угол, образованный двумя касательными к окружности | 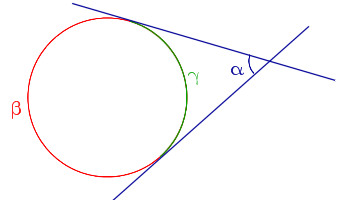 | Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами Посмотреть доказательство |  |
| Угол, образованный пересекающимися хордами хордами |
 |
Формула:  |
Теорема Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами. Посмотреть доказательство |
| Угол, образованный секущими секущими, которые пересекаются вне круга |
  |
Формула: 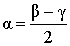 |
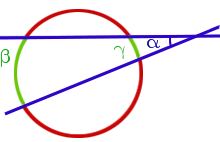
Теорема Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами Посмотреть доказательство |
| Угол, образованный касательной и хордой хордой, проходящей через точку касания |
 |
Формула: 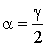 |
Теорема Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами Посмотреть доказательство |
| Угол, образованный касательной и секущей касательной и секущей |
  |
Формула: 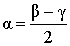 |
Теорема Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами Посмотреть доказательство |
| Угол, образованный двумя касательными касательными к окружности |
  |
Формулы:  |
Теорема Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами Посмотреть доказательство |
Доказательства теорем об углах, связанных с окружностью
Теорема 1. Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.
Доказательство. Рассмотрим сначала вписанный угол ABC, сторона BC которого является диаметром окружности диаметром окружности, и центральный угол AOC (рис. 5).

Рис. 5
Так как отрезки AO и BO являются радиусами окружности радиусами окружности, то треугольник AOB – равнобедренный, и угол ABO равен углу OAB. Поскольку угол AOC является внешним углом треугольника AOB, то справедливы равенства

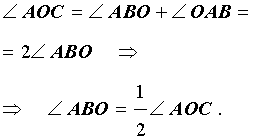

Таким образом, в случае, когда одна из сторон вписанного угла проходит через центр окружности, теорема 1 доказана.
Теперь рассмотрим случай, когда центр окружности лежит внутри вписанного угла (рис. 6).

Рис. 6
В этом случае справедливы равенства

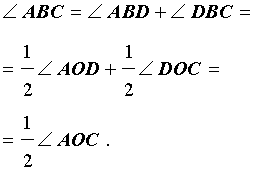

и теорема 1 в этом случае доказана.
Осталось рассмотреть случай, когда центр окружности лежит вне вписанного угла (рис. 7).
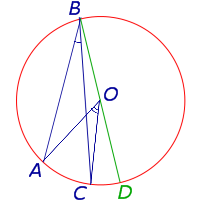
Рис. 7
В этом случае справедливы равенства
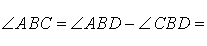
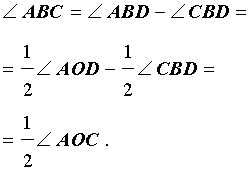

что и завершает доказательство теоремы 1.
Теорема 2. Величина угла, образованного пересекающимися хордами хордами, равна половине суммы величин дуг, заключённых между его сторонами.
Доказательство. Рассмотрим рисунок 8.
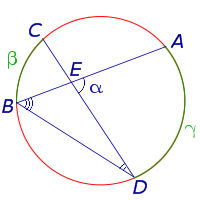
Рис. 8
Нас интересует величина угла AED, образованного пересекающимися в точке E хордами AB и CD. Поскольку угол AED – внешний угол треугольника BED, а углы CDB и ABD являются вписанными углами, то справедливы равенства


что и требовалось доказать.
Теорема 3. Величина угла, образованного секущими секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между сторонами этого угла.
Доказательство. Рассмотрим рисунок 9.

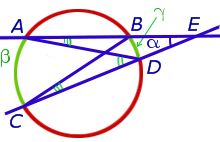
Рис. 9
Нас интересует величина угла BED, образованного пересекающимися в точке E секущими AB и CD. Поскольку угол ADC – внешний угол треугольника ADE, а углы ADC , DCB и DAB являются вписанными углами, то справедливы равенства

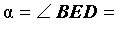
что и требовалось доказать.
Теорема 4. Величина угла, образованного касательной и хордой касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами.
Доказательство. Рассмотрим рисунок 10.


Рис. 10
Нас интересует величина угла BAC , образованного касательной AB и хордой AC . Поскольку AD – диаметр диаметр, проходящий через точку касания, а угол ACD – вписанный угол, опирающийся на диаметр, то углы DAB и DCA – прямые. Поэтому справедливы равенства
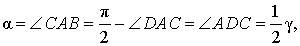

что и требовалось доказать
Теорема 5. Величина угла, образованного касательной и секущей касательной и секущей, равна половине разности величин дуг, заключённых между сторонами этого угла.
Доказательство. Рассмотрим рисунок 11.


Рис. 11
Нас интересует величина угла BED, образованного касательной AB и секущей CD. Заметим, что угол BDC – внешний угол треугольника DBE, а углы BDC и BCD являются вписанными углами. Кроме того, углы DBE и DCB, в силу теоремы 4, равны. Поэтому справедливы равенства
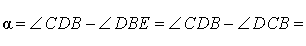

что и требовалось доказать.
Теорема 6.Величина угла, образованного двумя касательными к окружности касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами.
Доказательство. Рассмотрим рисунок 12.


Рис. 12
Нас интересует величина угла BED, образованного касательными AB и CD. Заметим, что углы BOD и BED в сумме составляют π радиан. Поэтому справедливо равенство
α = π – γ .
Далее получаем

что и требовалось доказать.

На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Углы многоугольника. Сумма внешних и внутренних углов
Внутренний угол многоугольника – это угол, образованный двумя смежными сторонами многоугольника. Например, ∠ABC является внутренним углом.

Внешний угол многоугольника – это угол, образованный одной стороной многоугольника и продолжением другой стороны. Например, ∠LBC является внешним углом.

Количество углов многоугольника всегда равно количеству его сторон. Это относится и к внутренним углам и к внешним. Несмотря на то, что для каждой вершины многоугольника можно построить два равных внешних угла, из них всегда принимается во внимание только один. Следовательно, чтобы найти количество углов любого многоугольника, надо посчитать количество его сторон.
Сумма внутренних углов
Сумма внутренних углов выпуклого многоугольника равна произведению 180° и количеству сторон без двух.
s = 2d(n — 2)
где s – это сумма углов, 2d – два прямых угла (то есть 2 · 90 = 180°), а n – количество сторон.
Если мы проведём из вершины A многоугольника ABCDEF все возможные диагонали, то разделим его на треугольники, количество которых будет на два меньше, чем сторон многоугольника:

Следовательно, сумма углов многоугольника будет равна сумме углов всех получившихся треугольников. Так как сумма углов каждого треугольника равна 180° (2d), то сумма углов всех треугольников будет равна произведению 2d на их количество:
s = 2d(n — 2) = 180 · 4 = 720°
Из этой формулы следует, что сумма внутренних углов является постоянной величиной и зависит от количества сторон многоугольника.
Сумма внешних углов
Сумма внешних углов выпуклого многоугольника равна 360° (или 4d).
s = 4d
где s – это сумма внешних углов, 4d – четыре прямых угла (то есть 4 · 90 = 360°).
Сумма внешнего и внутреннего угла при каждой вершине многоугольника равна 180° (2d), так как они являются смежными углами. Например, ∠1 и ∠2:

Следовательно, если многоугольник имеет n сторон (и n вершин), то сумма внешних и внутренних углов при всех n вершинах будет равна 2dn. Чтобы из этой суммы 2dn получить только сумму внешних углов, надо из неё вычесть сумму внутренних углов, то есть 2d(n — 2):
s = 2dn — 2d(n — 2) = 2dn — 2dn + 4d = 4d
Теорема о внешнем угле треугольника — Википедия
Материал из Википедии — свободной энциклопедии
Теорема о внешнем угле треугольника — одна из основных теорем планиметрии.
Внешний углом плоского треугольника при данной вершине называется угол, смежный с её внутренним углом внутреннему углу треугольника при этой вершине (см. рис.). Если внутренний угол при данной вершине треугольника образован двумя сторонами, выходящими из данной вершины, то внешний угол треугольника образован одной стороной, выходящей из данной вершины и продолжением другой стороны, выходящей из той же вершины.
- Внешний угол равен разности между 180° и внутренним углом, он может принимать значения от 0 до 180° не включительно.
- Теорема о внешнем угле треугольника: Внешний угол треугольника равен сумме двух оставшихся углов треугольника, не смежных с этим внешним углом. Иными словами, (см. рис.): d=a+c.{\displaystyle d=a+c.}
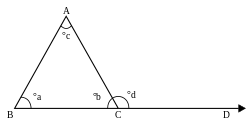 Внешним углом DCA плоского треугольника ABC при данной вершине C называется угол, смежный внутреннему углу ACB треугольника при этой вершине
Внешним углом DCA плоского треугольника ABC при данной вершине C называется угол, смежный внутреннему углу ACB треугольника при этой вершинеДоказательство (в обозначениях рис. выше)[править | править код]
Утверждение теоремы следует из теоремы о сумме углов треугольника, равной 180°.
Пусть ABC — произвольный треугольник с внешним углом d. Так как углы b и d — смежные, то их сумма равна 180°, то есть угол d = 180° — b. По теореме о сумме углов треугольника, угол b = 180° — (a + c). Из этого следует, что углы a + c = 180 — b. Так как d также равен 180 — b, то угол d = a + c. Что и требовалось доказать.
С другой стороны, если выполняется Теорема о внешнем угле треугольника, тогда справедливы следующая логическая цепь равенств:
- d=a+c{\displaystyle d=a+c}
- b+d=180∘=>{\displaystyle b+d=180^{\circ }=>}
- b+a+c=180∘.{\displaystyle b+a+c=180^{\circ }.}.
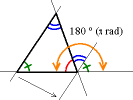 Иллюстрация к евклидовому доказательству теоремы о внешнем угле треугольника
Иллюстрация к евклидовому доказательству теоремы о внешнем угле треугольникаВ евклидовом доказательстве теоремы о внешнем угле треугольника, принадлежащем Евклиду, (а также и результата о том, то сумма всех трех внутренних углов треугольника равна 180°) сначала проводится прямая, параллельна стороне AB, проходящая через вершину C, а затем, используя свойство соответственных углов при двух параллельных прямых и одной секущей и о внутренних накрест лежащих углах при двух параллельных прямых, требуемое утверждение получают как иллюстрацию (см. рис.).[1].
Теорема о внешнем угле треугольника используется тогда, когда пытаются вычислить меры неизвестных углов в геометрии, в задачах с многоугольниками, где используются треугольники.
- Faber, Richard L. (1983), Foundations of Euclidean and Non-Euclidean Geometry, New York: Marcel Dekker, Inc., ISBN 0-8247-1748-1
- Greenberg, Marvin Jay (1974), Euclidean and Non-Euclidean Geometries/Development and History, San Francisco: W.H. Freeman, ISBN 0-7167-0454-4
- Heath, Thomas L. (англ.)русск.. The Thirteen Books of Euclid’s Elements (неопр.). — 2nd ed. [Facsimile. Original publication: Cambridge University Press, 1925]. — New York: Dover Publications, 1956.
- (3 vols.): ISBN 0-486-60088-2 (vol. 1), ISBN 0-486-60089-0 (vol. 2), ISBN 0-486-60090-4 (vol. 3).
- Henderson, David W. & Taimiņa, Daina (2005), Experiencing Geometry/Euclidean and Non-Euclidean with History (3rd ed.), Pearson/Prentice-Hall, ISBN 0-13-143748-8
- Venema, Gerard A. (2006), Foundations of Geometry, Upper Saddle River, NJ: Pearson Prentice Hall, ISBN 0-13-143700-3
- Wylie Jr., C.R. (1964), Foundations of Geometry, New York: McGraw-Hill
- Wheater, Carolyn C. (2007), Homework Helpers: Geometry, Franklin Lakes, NJ: Career Press, с. 88–90, ISBN 978-1-56414-936-7
Внутренний угол Википедия
 Тринадцатиугольник — многоугольник с 13 углами и 13 вершинами.
Тринадцатиугольник — многоугольник с 13 углами и 13 вершинами.Многоуго́льник — геометрическая фигура, обычно определяемая как часть плоскости, ограниченная замкнутой ломаной, звенья которой не пересекаются.
Варианты определений[ | ]
 Многоугольники
МногоугольникиСуществуют три различных варианта определения многоугольника; последнее определение является наиболее распространённым.
- Плоская замкнутая ломаная — наиболее общий случай;
- Плоская замкнутая ломаная без самопересечений, любые два соседних звена которой не лежат на одной прямой;
- Часть плоскости, ограниченная замкнутой ломаной без самопересечений — плоский многоугольник; в этом случае сама ломаная называется контуром многоугольника.
В любом случае вершины ломаной называются вершинами многоугольника, а её звенья — сторонами многоугольника.
Связанные определения[ | ]
- Вершины многоугольника называются соседними, если они являются концами одной из его сторон.
- Стороны многоугольника называются смежными, если они прилегают к одной вершине.
- Отрезки, соединяющие несоседние вершины многоугольника, называются диагоналями.
- Углом (или внутренним углом) многоугольника при данной вершине называется угол, образованный его сторонами, сходящимися в этой вершине, и находящийся во внутренней области многоугольника. В частности, угол может превосходить 180°, если многоугольник невыпуклый.
- Внешним углом выпуклого многоугольника при данной вершине называется угол, смежный внутреннему углу многоугольника при этой вершине. В общем случае внешний угол — разность между 180° и внутренним углом, он может принимать значения от −180° до 180°.
