Расчет радиуса круговой кривой по стрелам изгиба — геодезия
Радиус круговой кривой может быть выражен через стрелу изгиба по общеизвестной формуле:
т.е. величину стрелы изгиба можно рассматривать как кривизну, выраженную в определенном масштабе.
Положение в плане точек деления существующей кривой, а также проектной кривой относительно касательной АВ может быть установлено по величине отрезков 1—2, 2—5, 3—4 и т.д., равных ΔK, и углам поворота этих отрезков α1, α2, α3 и т.д.
Для расчета величин сдвижек железнодорожных кривых целесообразно выражать положение точек деления кривой в плане относительно касательной АВ через длину их эвольвент ω: 2′—2; 3’—3; 4’—4 … (см. рис. 48), которые для соответствующих точек равны:
Выражая в последней формуле величины углов поворота через стрелы изгиба согласно равенствам (III.22), в результате чего ΔK сократится, получим следующие формулы для длины эвольвенты:
Если сумму статических моментов стрел выразить через момент суммы стрел (через момент равнодействующей), то длина эвольвенты будет равна:
§
Стрела прогиба — это… Что такое Стрела прогиба?
- Стрела прогиба
максимальное смещение оси изгибаемого конструктивного элемента (балки, фермы, ригеля и т.п.) под действием внешних сил в направлении, перпендикулярном оси. Величина С. п. ограничивается нормами на проектирование строительных конструкций.
Большая советская энциклопедия. — М.: Советская энциклопедия. 1969—1978.
- Стрела подъёма
- Стрела-змея
Смотреть что такое «Стрела прогиба» в других словарях:
стрела прогиба — (строит.), максимальное смещение оси изгибаемого конструктивного элемента (балки, ригеля рамы, пояса фермы и т. п.) под действием внешних сил в направлении, перпендикулярном оси. Величина стрелы прогиба ограничивается нормами на проектирование… … Энциклопедический словарь
Стрела прогиба — – максимальное смещение по вертикали продольной оси срединной поверхности изгибаемого элемента от первоначального положения. [Большой энциклопедический политехнический словарь.] Стрела прогиба – максимальное смещение оси изгибаемого… … Энциклопедия терминов, определений и пояснений строительных материалов
СТРЕЛА ПРОГИБА — в строительстве максимальное смещение оси изгибаемого конструктивного элемента (балки, ригеля рамы, пояса фермы и т. п.) под действием внешних сил в направлении, перпендикулярном оси. Величина стрелы прогиба ограничивается нормами на… … Большой Энциклопедический словарь
СТРЕЛА ПРОГИБА — наибольший прогиб при изгибе бруса или пластины. Величина С. п. зависит от рода и формы тела, подвергнутого изгибу, а также от величины и распределения изгибающих сил. Технический железнодорожный словарь. М.: Государственное транспортное… … Технический железнодорожный словарь
СТРЕЛА ПРОГИБА — Макс. смещение оси изгибаемого конструктивного элемента (балки, фермы, ригеля и т. п.) под действием внеш. сил в направлении, перпендикулярном оси. Размер С. п. обычно нормируется … Большой энциклопедический политехнический словарь
СТРЕЛА ПРОГИБА — максимальное смещение по вертикали продольной оси срединной поверхности изгибаемого элемента от первоначального положения (Болгарский язык; Български) стрелка на огъването (Чешский язык; Čeština) průhyb (Немецкий язык; Deutsch) Durchbiegung;… … Строительный словарь
СТРЕЛА ПРОГИБА — максимальное смещение оси образца при изгибе. Одна из характеристик механических свойств чугунов … Металлургический словарь
стрела прогиба бандажа — 3.2 стрела прогиба бандажа: Разница между фактическими значениями внутреннего диаметра бандажа, измеренными по оси приложения нагрузки, до и после проведения испытания на конструкционную прочность. Источник: ГОСТ 398 2010: Бандажи черновые для… … Словарь-справочник терминов нормативно-технической документации
кривизна трубы общая (стрела прогиба) — 3.12 кривизна трубы общая (стрела прогиба): Максимальное смещение оси трубы в перпендикулярном ей направлении. Источник: СТО Газпром 2 4.1 228 2008: Технические требования к насосно компрессорным трубам для месторождений ОАО «Газпром» … Словарь-справочник терминов нормативно-технической документации
Ндп. Относительная стрела прогиба пера — Источник: ГОСТ 23537 79: Лопатки авиационных осевых компрессоров и турбин. Термины и определения оригинал документа … Словарь-справочник терминов нормативно-технической документации
Определение зависимости стрелы прогиба от нагрузки. — Студопедия.Нет
Определение модуля упругости кости по изгибу
Цель работы: изучение упругих свойств костной ткани,определение
модуля упругости костной ткани человека, дюралюминия и пластмассы.
В некоторых областях медицины, особенно в хирургии и ортопедии, при изучении опорно-двигательного аппарата человека, в вопросах протезирования важным является знание упругих свойств тканей организма и, в частности, костной ткани. Например, знание упругих характеристик костей необходимо для подбора нагрузок при вытяжениях.
Деформация-это изменение взаимного положения точек тела. Деформации могут возникать в твёрдых телах при воздействии внешних сил. При этом изменяются форма и размер тела и в теле возникают упругие силы, которые создают механическое напряжение 
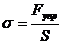
 , где Fупр— упругая сила; S- площадь сечения тела. В СИ размерность σ — Н/м2. В зависимости от изменения формы тела под действием внешних сил различают следующие виды деформации: растяжение, сжатие, сдвиг, кручение и изгиб. Если после прекращения действия внешних сил тело восстанавливает свою форму, то деформация называется
, где Fупр— упругая сила; S- площадь сечения тела. В СИ размерность σ — Н/м2. В зависимости от изменения формы тела под действием внешних сил различают следующие виды деформации: растяжение, сжатие, сдвиг, кручение и изгиб. Если после прекращения действия внешних сил тело восстанавливает свою форму, то деформация называется 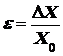 .
.
Для упругих деформаций справедлив закон Гука:
, или 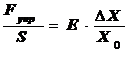
где E – модуль упругости (модуль Юнга).
При ΔX=X модуль упругости 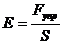 . Отсюда следует, что модуль Юнга численно равен механическому напряжению, возникающему в теле при относительной деформации равной единице, т.е. при увеличении размеров тела в два раза.
. Отсюда следует, что модуль Юнга численно равен механическому напряжению, возникающему в теле при относительной деформации равной единице, т.е. при увеличении размеров тела в два раза.
В широком интервале изменения величины внешних нагрузок зависимость механического напряжения в образце от его относительной деформации достаточно сложная, она определяется свойствами материала и не всегда подчиняется закону Гука .

На участке ОАВ деформация является упругой, но зависимость между s и ε на участке АВ становится нелинейной, поэтому точке А соответствует предел пропорциональности sпроп, а точке В – предел упругости sупр, поскольку при
На участке СК относительное удлинение ε образца растет при почти постоянном механическом напряжении, поэтому его называют участком (площадкой) текучести, а напряжение sт, с которого он начинается, – пределом текучести.
Следует подчеркнуть, что пластическое течение материала возникает только в том случае, когда действующие внешние силы становятся не меньше некоторого предела, соответствующего пределу текучести. Это отличает пластическое течение материала от течения вязкой жидкости, которое происходит под действием любых сил, как бы малы они не были.
На участке КД образец опять оказывает сопротивление деформации (т.е. s увеличивается с увеличением ε) и точке Д соответствует предел прочности (временное сопротивление) sпроч – это величина механического напряжения в образце, после которого он начинает необратимо разрушаться, так что на участке ДЕ относительная деформация растет даже при снижении механического напряжения. Прочность костей – показатель, без которого не может обойтись судебно-медицинская экспертиза.
Строение костной ткани достаточно сложно. В компактной костной ткани половину объёма составляет неорганический материал – гидроксилапатит. Это вещество представлено в форме микроскопических кристалликов. Другая часть объёма состоит из органического материала, главным образом коллагена(высокомолекулярное соединение, волокнистый белок, обладающий высокой эластичностью). Коллаген в кости образует фибриллы – тонкие длинные нити. Кристаллы неорганических веществ расположены между фибриллами и прочно прикреплены к ним. Способность кости к упругой деформации реализуется за счёт минерального вещества, а текучесть(пластическое деформирование) — за счёт коллагена.
Механические свойства костной ткани зависят от многих факторов: возраста, заболевания, индивидуальных условий роста. В норме плотность костной ткани 2400 кг/м3, а её модуль Юнга 2∙1010 Па; предел прочности при растяжении sпроч=100 МПа, относительная деформация достигает 1%.
При различных способах деформирования кость ведёт себя по-разному. Прочность на сжатие выше, чем на растяжение или изгиб. Так бедренная кость в продольном направлении выдерживает нагрузку 45000 Н, а при изгибе – 2500 Н.
Запас механической прочности весьма значителен и заметно превышает нагрузки, с которыми она встречается в обычных жизненных условиях. Живая кость в 5 раз прочнее железобетона. Бедренная и берцовая кости выдерживают нагрузку в 25-30 раз больше веса нормального человека.
Определение модуля упругости материала.
Существуют различные методы определения модуля упругости. В данной работе модуль упругости определяется из деформации изгиба.
Изгибом образца (стержня) называется деформация, при которой изменяется кривизна продольной оси образца (рис.2). Прямой стержень, работающий главным образом на изгиб, принято называть балкой. На рисунке 2 изображён стержень АВ, закрепленный одним концом в стене. Под влиянием силы Р он изгибается, как показано пунктиром. Расстояние между концами изогнутого и неизогнутого стержня называется стрелой прогиба f. Она является мерой деформации изгиба.

Под влиянием силы Р, изгибающей стержень книзу, его верхние слои растягиваются, нижние сжимаются, а на каком-то уровне по высоте стержня остается средний, нейтральный, слой, не изменяющий своей длины.
В теории сопротивления материалов доказывается, что если к одному из концов стержня длиной L, шириной b, и высотой h приложить нагрузку P, а другой конец закрепить, то стрелу прогиба f находят по формуле:
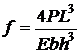
Откуда
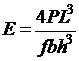 (2)
(2)
|

Описание установки. Установка для определения стрелы прогиба состоит из штатива, на котором закрепляются образец костной ткани и индикатор (рис.3.) У края образца закреплён крючок. При подвешивании на крючок грузов определённой величины кость будет прогибаться. Величину прогиба фиксирует индикатор. С помощью индикатора измеряют стрелу прогиба с точностью до 0,01 мм (работа индикатора рассматривается в лабораторной работе № 3).
Порядок выполнения лабораторной работы.
Определение зависимости стрелы прогиба от нагрузки.
1. Закрепите образец на штативе с помощью держателя.
2. Приведите в соприкосновение измерительную штангу индикатора с верхней поверхностью образца в месте крепления крючка на образце.
3. Установите стрелку индикатора в нулевое положение.
4. Нагружайте образец, путём подвешивания на крючок грузов.
5. Отмечайте для каждого груза соответствующую стрелу прогиба.
6. Результаты опыта занесите в таблицу 1.
7. По найденным значениям стрелы прогиба и соответствующим нагрузкам постройте график. Для этого по оси абсцисс откладывают нагрузку, а по оси ординат – стрелу прогиба.
Таблица 1.
Нагрузка
Материал | P=1Н | P=2Н | P=3Н | P=4Н | P=5Н | Р=6Н | ΣРi=21 |
| f,мм | f,мм | f,мм | f,мм | f,мм | f,мм | Σfi мм | |
| Кость | |||||||
| Дюраль | |||||||
| Гетинакс |
8. Под графиком запишите вывод относительно полученной зависимости.
Определение — стрела — прогиб
Определение — стрела — прогиб
Cтраница 1
Определение стрелы прогиба и предела прочности при сжатии-факультативно, если оно не оговорено ТУ заказа. [2]
Кроме определения стрелы прогиба и напряжений смятия иногда определяют суммарные напряжения сг2, возникающие в распределительном вале от совместного действия изгибающего и скручивающего моментов. [3]
Кроме определения стрелы прогиба и напряжений смятия иногда определяют суммарные напряжения as, возникающие в распределительном вале от совместного действия изгибающего и скручивающего моментов. [4]
Для определения стрелы прогиба лист материала кладут Йогнутой стороной вверх на горизонтальную плоскость. Параллельно краю листа прикладывают линейку с предпочтительной длиной 1000 мм. Масса линейки не должна оказывать влияния на результат измерения. Измеряют максимальное расстояние ( просвет) между линейкой и поверхностью листа. [5]
Для определения стрелы прогиба ремня необходимо приложить к ремню линейку и нажимать большим пальцем на ремень в его средней части с усилием: для двигателей автомобилей ГАЗ и ЗИЛ-3-4, для ЯМЗ — около 10 кгс, установив, таким образом, на сколько миллиметров прогнулся ремень. [6]
Для определения стрелы прогиба ремня необходимо приложить к ремню линейку и нажать большим пальцем на ремень в его средней части с усилием: для двигателей автомобилей ГАЗ и ЗИЛ — 3 — 4, для ЯМЗ — около 10 кгс, при этом прогиб ремня у двигателей ГАЗ должен быть 12 — 20, у ЗИЛ-120, 121 и ГАЗ-21 — 10 — 15, у ЯМЗ — 13 — 19, у автомобилей ЗИЛ-158, Урал-15 — 20 мм. [7]
При определении стрелы прогиба ступенчатых валов в расчет принимают некоторый усредненный диаметр. [8]
Формула (16.31) для определения стрелы прогиба в середине стержня при внецентренном приложении нагрузки является приближенной, так как изогнутая ось стержня принята в виде полуволны синусоиды. [9]
Контроль изогнутости требует определения стрелы прогиба в продольном сечении изделия при прокручивании его на ножах. [10]
Особенностью расчета этих шеверов является определение стрелы прогиба боковой поверхности зубьев и изменения толщины зуба по длине шевера. Если стрелу прогиба облегающего шевера увеличить, то при обработке на колесах образуются зубья бочкообразной формы ( фиг. Бочкообразные зубья уменьшаются ( по толщине) от середины к торцам колеса на 0 01 — 0 03 мм. Колеса с бочкообразными зубьями менее чувствительны к перекосу осей передачи, обеспечивают положение пятна касания посередине зуба, способствуют уменьшению шума передачи и других недостатков. Колеса с бочкообразными зубьями могут быть обработаны и обычными шеверами, но на станках со специальным устройством. [11]
Особенностью расчета этих шеверов является определение стрелы прогиба боковой поверхности зубьев и изменения толщины зуба по длине шевера. Если стрелу прогиба облегающего шевера увеличить, то при обработке на колесах образуются зубья бочкообразной формы ( фиг. Бочкообразные зубья уменьшаются ( по толщине) от середины к торцам колеса на 0 01 — 0 03 мм. Колеса — с бочкообразными зубьями менее чувствительны к перекосу осей передачи, обеспечивают положение пятна касания посередине зуба, способствуют уменьшению шума передачи и других недостатков. Колеса с бочкообразными зубьями могут быть обработаны и обычными шеверами, но на станках со специальным устройством. [12]
При заводских испытаниях рессор обычно ограничиваются определением стрелы прогиба рессоры при заданной рабочей нагрузке. [13]
На рис. 3 — 5 приведены данные для определения стрелы прогиба, напряжений в срединной поверхности и напряжений изгиба для квадратной пластинки по результатам уточненного решения [2]; на рис. 4 — 5 обозначено: А — угол пластинки; С — центр.
стрела прогиба — это… Что такое стрела прогиба?
- стрела прогиба
- стрела́ проги́ба
(строит.), максимальное смещение оси изгибаемого конструктивного элемента (балки, ригеля рамы, пояса фермы и т. п.) под действием внешних сил в направлении, перпендикулярном оси. Величина стрелы прогиба ограничивается нормами на проектирование строительных конструкций.
* * *
СТРЕЛА ПРОГИБАСТРЕЛА́ ПРОГИ́БА, в строительстве — максимальное смещение оси изгибаемого конструктивного элемента (балки, ригеля рамы, пояса фермы и т. п.) под действием внешних сил в направлении, перпендикулярном оси. Величина стрелы прогиба ограничивается нормами на проектирование строительных конструкций.
Энциклопедический словарь. 2009.
- стрела подъёма
- стрела-змея
Смотреть что такое «стрела прогиба» в других словарях:
Стрела прогиба — – максимальное смещение по вертикали продольной оси срединной поверхности изгибаемого элемента от первоначального положения. [Большой энциклопедический политехнический словарь.] Стрела прогиба – максимальное смещение оси изгибаемого… … Энциклопедия терминов, определений и пояснений строительных материалов
СТРЕЛА ПРОГИБА — в строительстве максимальное смещение оси изгибаемого конструктивного элемента (балки, ригеля рамы, пояса фермы и т. п.) под действием внешних сил в направлении, перпендикулярном оси. Величина стрелы прогиба ограничивается нормами на… … Большой Энциклопедический словарь
СТРЕЛА ПРОГИБА — наибольший прогиб при изгибе бруса или пластины. Величина С. п. зависит от рода и формы тела, подвергнутого изгибу, а также от величины и распределения изгибающих сил. Технический железнодорожный словарь. М.: Государственное транспортное… … Технический железнодорожный словарь
Стрела прогиба — максимальное смещение оси изгибаемого конструктивного элемента (балки, фермы, ригеля и т.п.) под действием внешних сил в направлении, перпендикулярном оси. Величина С. п. ограничивается нормами на проектирование строительных конструкций … Большая советская энциклопедия
СТРЕЛА ПРОГИБА — Макс. смещение оси изгибаемого конструктивного элемента (балки, фермы, ригеля и т. п.) под действием внеш. сил в направлении, перпендикулярном оси. Размер С. п. обычно нормируется … Большой энциклопедический политехнический словарь
СТРЕЛА ПРОГИБА — максимальное смещение по вертикали продольной оси срединной поверхности изгибаемого элемента от первоначального положения (Болгарский язык; Български) стрелка на огъването (Чешский язык; Čeština) průhyb (Немецкий язык; Deutsch) Durchbiegung;… … Строительный словарь
СТРЕЛА ПРОГИБА — максимальное смещение оси образца при изгибе. Одна из характеристик механических свойств чугунов … Металлургический словарь
стрела прогиба бандажа — 3.2 стрела прогиба бандажа: Разница между фактическими значениями внутреннего диаметра бандажа, измеренными по оси приложения нагрузки, до и после проведения испытания на конструкционную прочность. Источник: ГОСТ 398 2010: Бандажи черновые для… … Словарь-справочник терминов нормативно-технической документации
кривизна трубы общая (стрела прогиба) — 3.12 кривизна трубы общая (стрела прогиба): Максимальное смещение оси трубы в перпендикулярном ей направлении. Источник: СТО Газпром 2 4.1 228 2008: Технические требования к насосно компрессорным трубам для месторождений ОАО «Газпром» … Словарь-справочник терминов нормативно-технической документации
Ндп. Относительная стрела прогиба пера — Источник: ГОСТ 23537 79: Лопатки авиационных осевых компрессоров и турбин. Термины и определения оригинал документа … Словарь-справочник терминов нормативно-технической документации
Тема 6 определение перемещений при изгибе. Расчет балок на жесткость
6.1. Понятие об упругой линии. Прогиб и угол поворота. Дифференциальное уравнение упругой линии. Условие жесткости при изгибе
Чтобы судить о работе изгибаемых балок, недостаточно знать только напряжения, которые возникают в сечениях балки от заданной нагрузки. Вычисленные напряжения позволяют проверить прочность системы. Однако весьма прочные балки могут оказаться непригодными к эксплуатации из-за недостаточной жесткости. Если балка при нагружении сильно прогибается, то при эксплуатации сооружения, имеющего гибкие балки, появятся затруднения и, кроме того, могут возникнуть колебания балки с большими амплитудами, а вместе с тем и значительные дополнительные напряжения.
Под жесткостью следует понимать способность элеменов конструкций и деталей машин сопротивляться внешним нагрузкам без видимых деформаций. Расчет на жесткость заключается в оценке упругой податливости балки под действием приложенных нагрузок и подбор таких размеров поперечного сечения, при которых перемещения не будут превышать установленных нормами пределов. Для выполнения такого расчета необходимо научиться вычислять перемещения сечений балки под действием любой внешней нагрузки.
Рассмотрим деформацию
балки при простом изгибе. Ось балки
(Рис.6.1,а) под действием нагрузки,
расположенной в одной из главных
плоскостей инерции (в плоскости 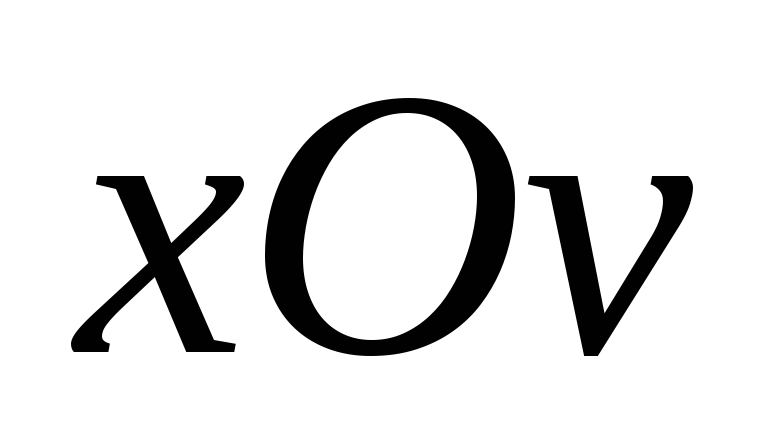 ),
искривляется в той же плоскости, а
поперечные сечения поворачиваются и
одновременно получают поступательные
перемещения. Искривленная ось балки
называетсяизогнутой
осью или упругой
линией. На рис.
6.1 упругая линия изображена тонкой
кривой.
),
искривляется в той же плоскости, а
поперечные сечения поворачиваются и
одновременно получают поступательные
перемещения. Искривленная ось балки
называетсяизогнутой
осью или упругой
линией. На рис.
6.1 упругая линия изображена тонкой
кривой.
Точка 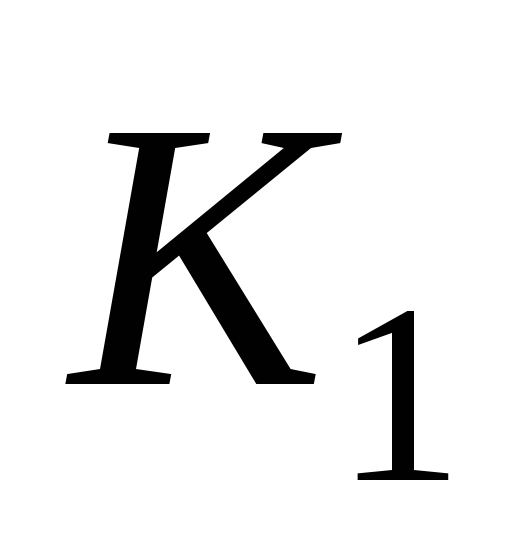 ,
лежащая на оси в сечении, отстоящем не
расстоянии
,
лежащая на оси в сечении, отстоящем не
расстоянии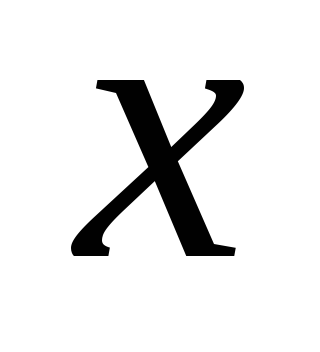 от начала координат, переместится в
точку
от начала координат, переместится в
точку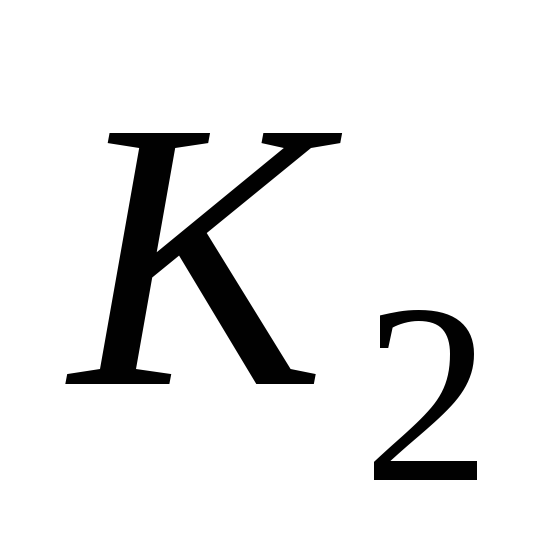 .
Обозначим перемещение произвольной
точки оси бруса в направлении оси
.
Обозначим перемещение произвольной
точки оси бруса в направлении оси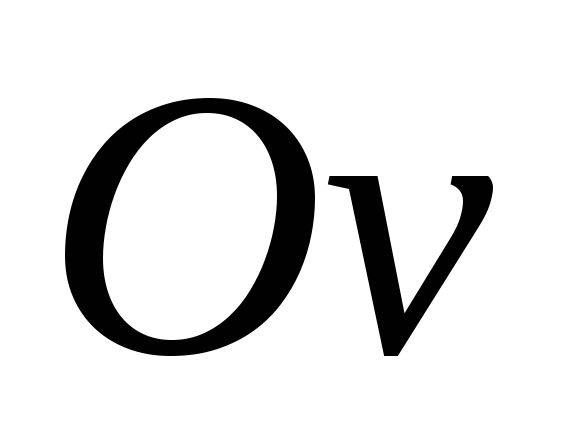 через
через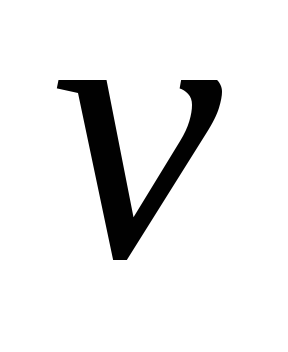 ,
а перемещение вдоль оси бруса – через
,
а перемещение вдоль оси бруса – через .
Если в точке
.
Если в точке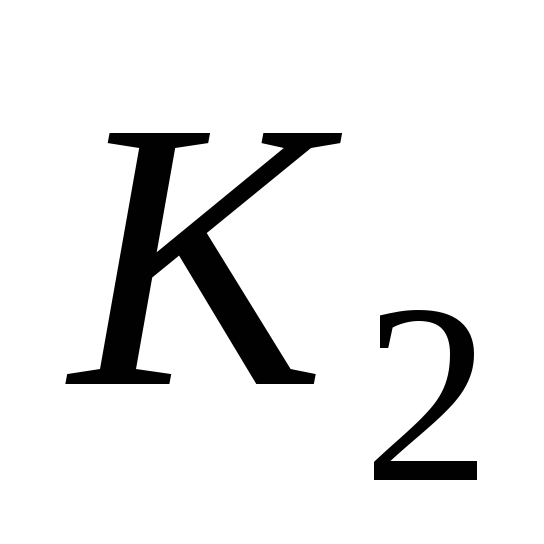 провести касательную к оси изогнутой
балки, то по отношению к первоначальному
положению оси она будет повернута на
угол
провести касательную к оси изогнутой
балки, то по отношению к первоначальному
положению оси она будет повернута на
угол .
Одновременно на тот же угол повернется
сечение в точке
.
Одновременно на тот же угол повернется
сечение в точке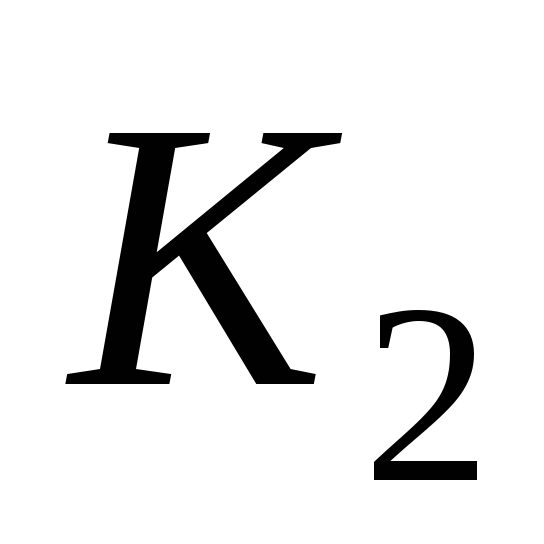 .
Таким образом, три величины
.
Таким образом, три величины 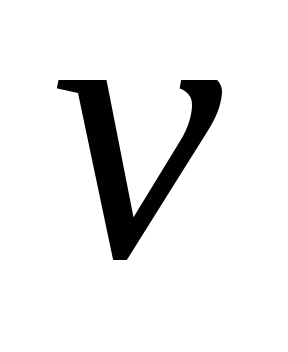 ,
, и
и являются компонентами перемещения
произвольного поперечного сечения
балки. Перемещение
являются компонентами перемещения
произвольного поперечного сечения
балки. Перемещение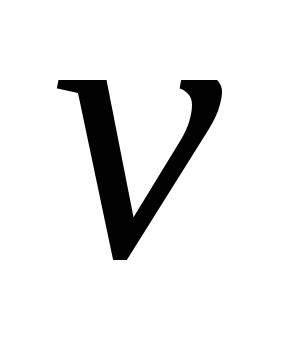 центра тяжести сечения по направлению,
перпендикулярному к оси балки, называетсяпрогибом.
Наибольший прогиб называется стрелой
прогиба и
обозначается буквой
центра тяжести сечения по направлению,
перпендикулярному к оси балки, называетсяпрогибом.
Наибольший прогиб называется стрелой
прогиба и
обозначается буквой 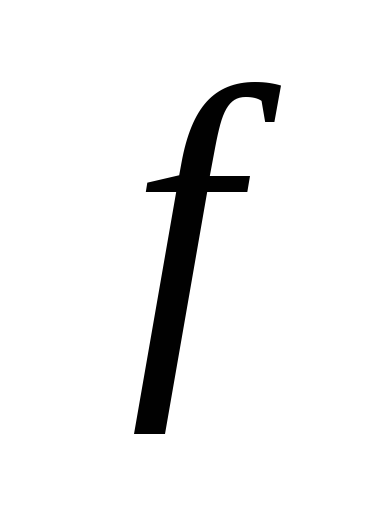 .
.
Угол  ,
на который каждое сечение поворачивается
по отношению к своему первоначальному
положению, называется углом поворота
сечения. Как уже отмечалось, угол поворота
также может быть определен как угол
между касательной к упругой линии и
осью
,
на который каждое сечение поворачивается
по отношению к своему первоначальному
положению, называется углом поворота
сечения. Как уже отмечалось, угол поворота
также может быть определен как угол
между касательной к упругой линии и
осью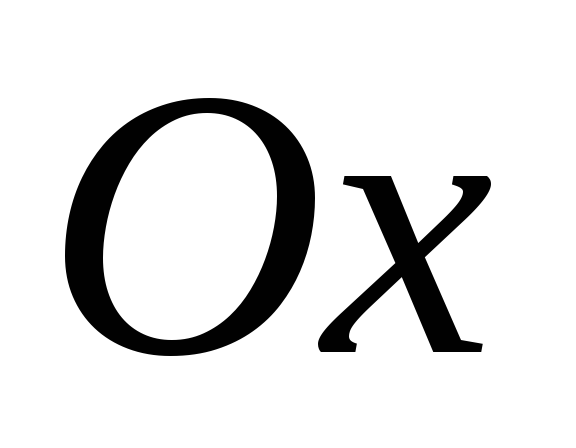 .
.

Рис.6.1
Проверка жесткости
балок сводится к требованию, в соответствии
с которым наибольший прогиб 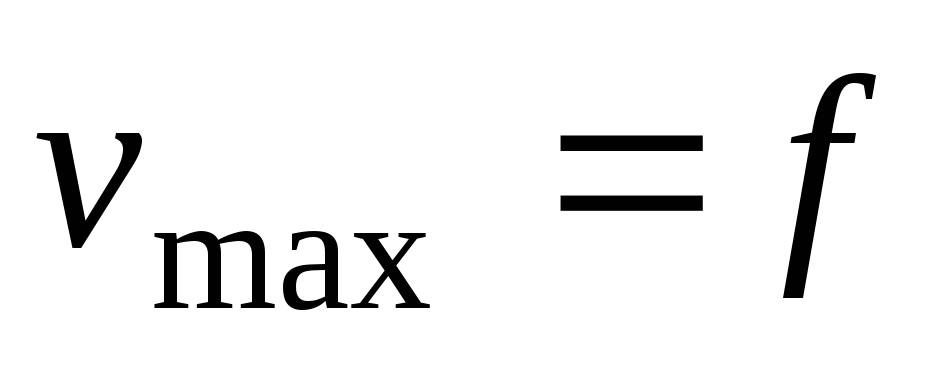 не должен превышать определенной доли
пролета:
не должен превышать определенной доли
пролета:
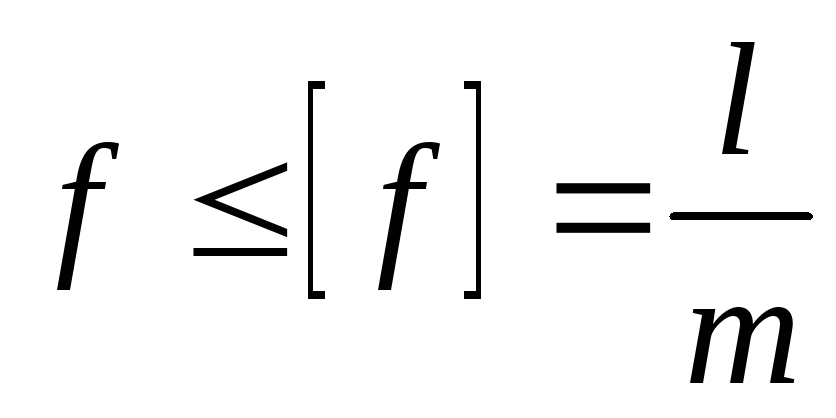 .
.
Число  устанавливается нормами проектирования
примерно в пределах от 300 до 1000. Для
ответственных сооружений, например,
для железнодорожных мостов, величина
устанавливается нормами проектирования
примерно в пределах от 300 до 1000. Для
ответственных сооружений, например,
для железнодорожных мостов, величина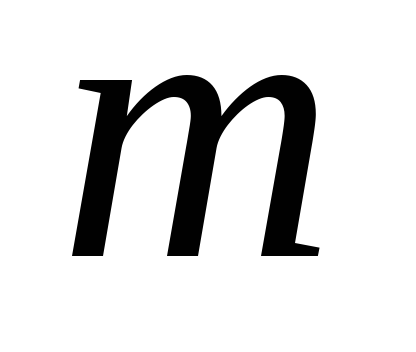 принимается равной 1000.
принимается равной 1000.
Отсюда видно, что
прогибы при изгибе, как правило, малы
по сравнению с пролетом балки. Это
позволяет внести некоторые упрощения.
Во-первых, при малых прогибах 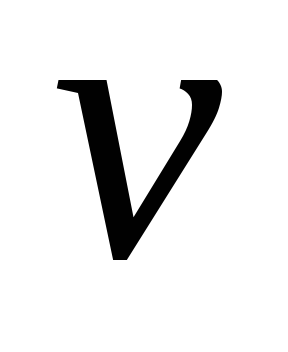 угол наклона касательной к оси изогнутой
балки можно определять с помощью
выражения:
угол наклона касательной к оси изогнутой
балки можно определять с помощью
выражения:
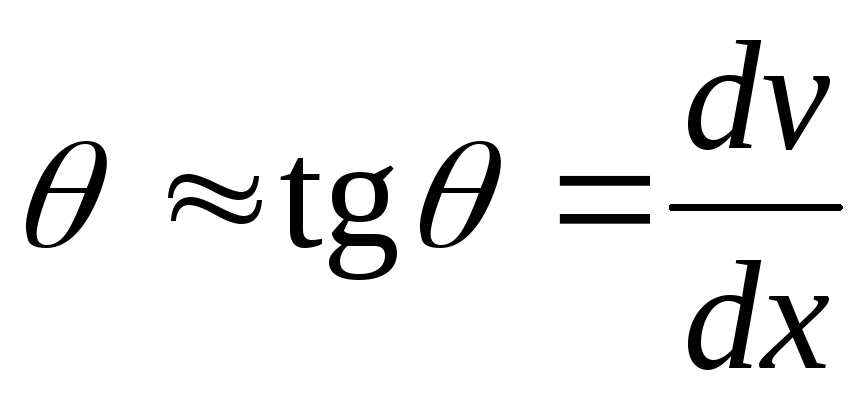 .
(6.1)
.
(6.1)
Во-вторых, горизонтальными
перемещениями  можно пренебречь, так как они существенно
меньше
можно пренебречь, так как они существенно
меньше (
(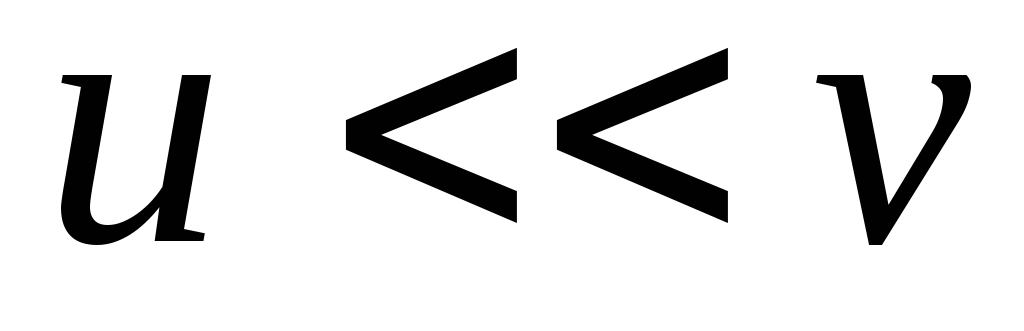 ).
В связи с этим при расчетах будем
пользоваться условной схемой перемещений,
изображенной на рис 6.1,б. Согласно этой
схеме каждая точка перемещается
перпендикулярно продольной оси бруса.
).
В связи с этим при расчетах будем
пользоваться условной схемой перемещений,
изображенной на рис 6.1,б. Согласно этой
схеме каждая точка перемещается
перпендикулярно продольной оси бруса.
Для определения полной картины деформаций необходимо получить уравнение упругой линии
 .
.
Исходя из физической природы изогнутой оси бруса, можем утверждать, что упругая линия должна быть непрерывной и гладкой кривой, следовательно, на протяжении всей оси бруса должны быть непрерывны функция и ее первая производная. Прогибы и углы поворота и являются перемещениями сечений балок при изгибе. Деформация того или иного участка балки определяется его кривизной.
При выводе формулы для нормальных напряжений при изгибе нами была получена связь между кривизной и изгибающим моментом:
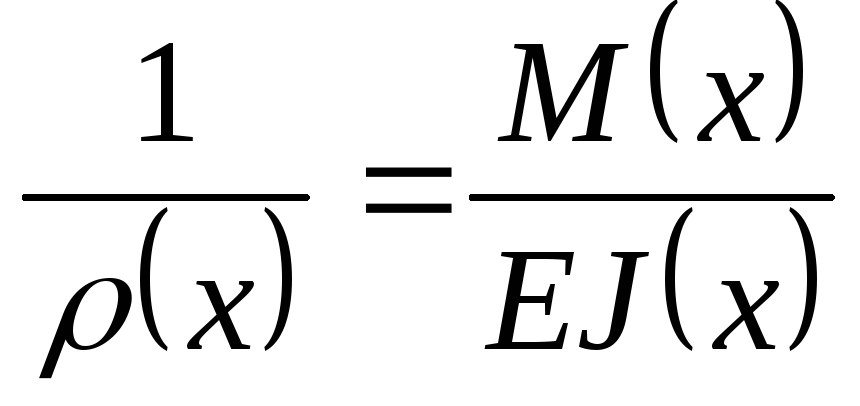 .
(6.2)
.
(6.2)
Из курса высшей математики известно следующее уравнение кривизны плоской кривой:
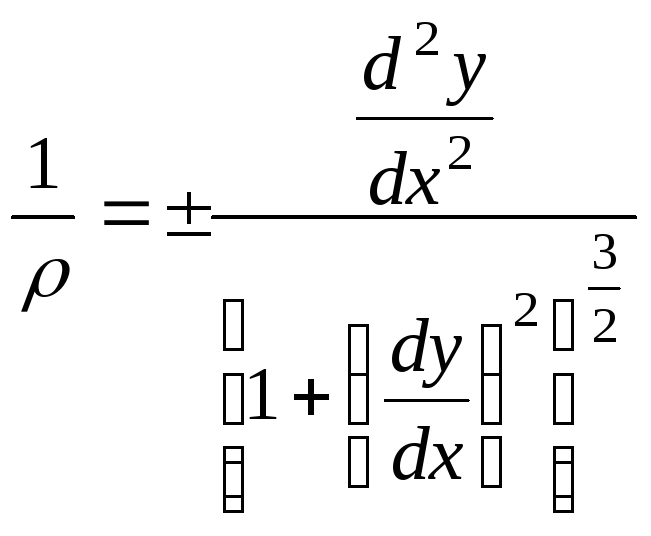 .
(6.3)
.
(6.3)
Подставляя значение
кривизны в равенство (6.2) и заменяя
координату  прогибом
прогибом ,
получим точное дифференциальное
уравнение упругой линии балки:
,
получим точное дифференциальное
уравнение упругой линии балки:
 .
(6.4)
.
(6.4)
Интегрирование этого
нелинейного дифференциального уравнения
связано с большими трудностями. Учитывая,
что на практике приходится иметь дело
с малыми прогибами и что тангенсы углов
наклона 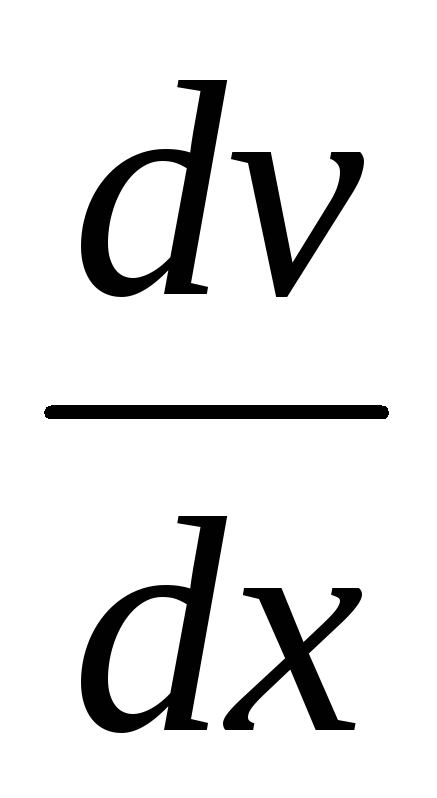 касательной к оси будут малы, квадратом
первой производной
касательной к оси будут малы, квадратом
первой производной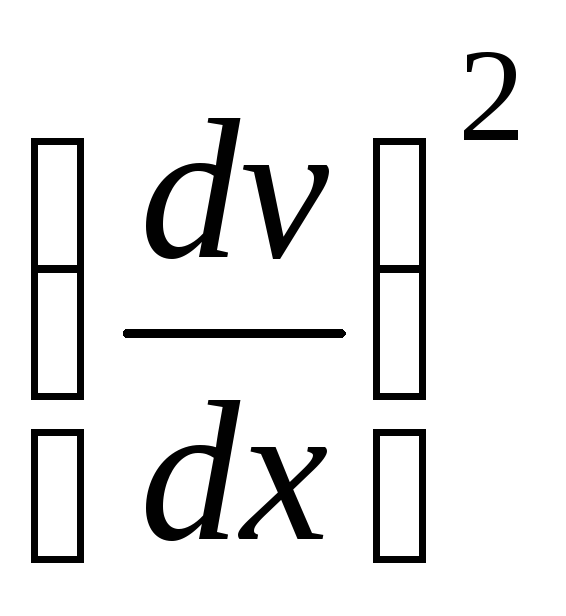 по
сравнению с единицей можно пренебречь.
Тогда получим приближенное (основное)
дифференциальное уравнение
по
сравнению с единицей можно пренебречь.
Тогда получим приближенное (основное)
дифференциальное уравнение
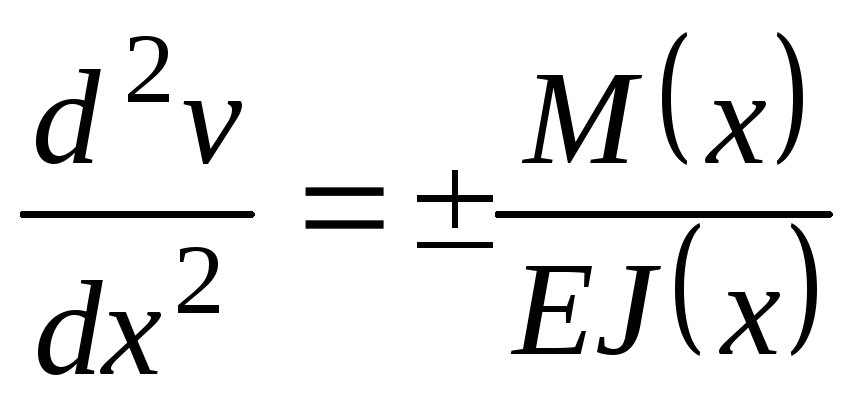 (6.5)
(6.5)
Два
знака в уравнении (6.5) поставлены потому,
что знак кривизны 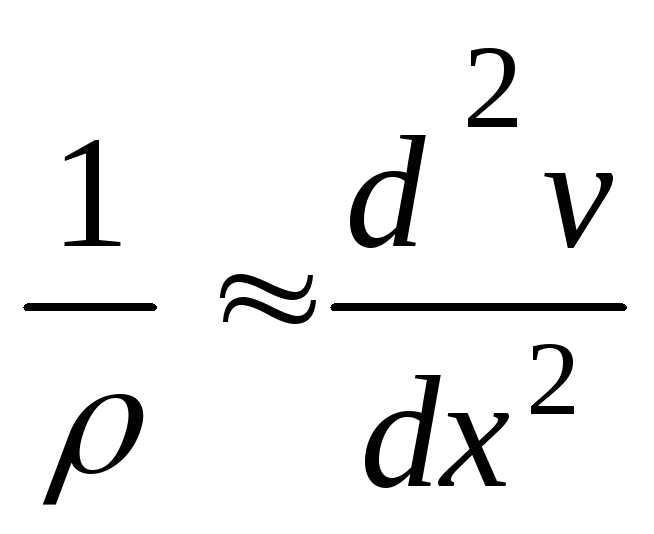 может не совпадать со знаком изгибающего
момента. Знак кривизны зависит от
направления осей координат. Знак
изгибающего момента был выбран в
зависимости от того, где расположены
растянутые волокна. Так, например, для
случая, когда ось
может не совпадать со знаком изгибающего
момента. Знак кривизны зависит от
направления осей координат. Знак
изгибающего момента был выбран в
зависимости от того, где расположены
растянутые волокна. Так, например, для
случая, когда ось направлена вверх, положительному моменту
(Рис.6.2,а) соответствует положительная
кривизна, а отрицательному – отрицательная
кривизна.
направлена вверх, положительному моменту
(Рис.6.2,а) соответствует положительная
кривизна, а отрицательному – отрицательная
кривизна.
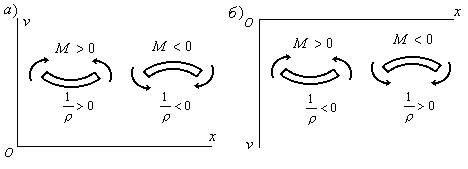
Рис 6.2
Таким
образом, в случае, когда ось  направлена вверх, знаки кривизны и
изгибающего момента совпадают. Поэтому
в дифференциальном уравнении берется
знак“+”.
Если ось
направлена вверх, знаки кривизны и
изгибающего момента совпадают. Поэтому
в дифференциальном уравнении берется
знак“+”.
Если ось 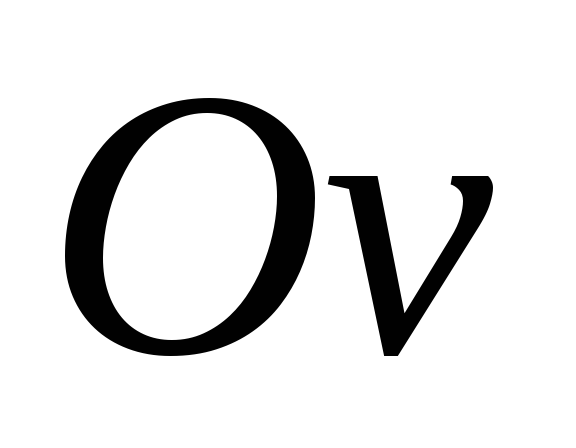 направлена вниз, то знаки у кривизны и
изгибающего момента будут различны
(Рис.6.2,б). Поэтому в этом случае в правой
части уравнения (6.5) берется знак“”.
направлена вниз, то знаки у кривизны и
изгибающего момента будут различны
(Рис.6.2,б). Поэтому в этом случае в правой
части уравнения (6.5) берется знак“”.
6.2. Метод непосредственного интегрирования приближенного (основного) дифференциального уравнения упругой линии
Решая
задачу аналитическим методом, углы
поворота 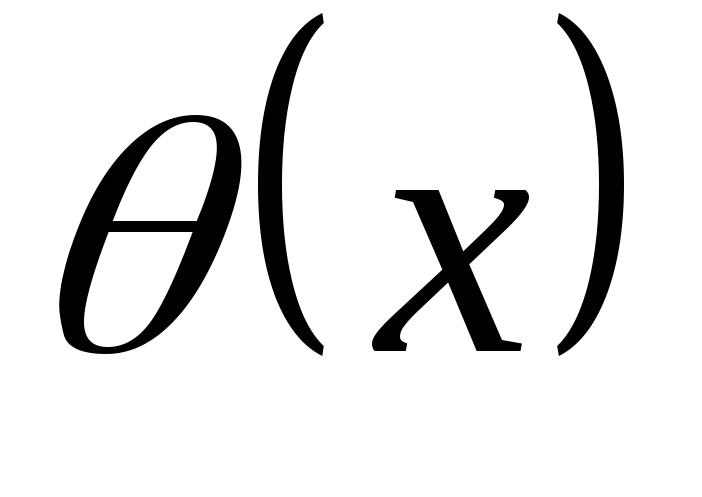 и прогибы
и прогибы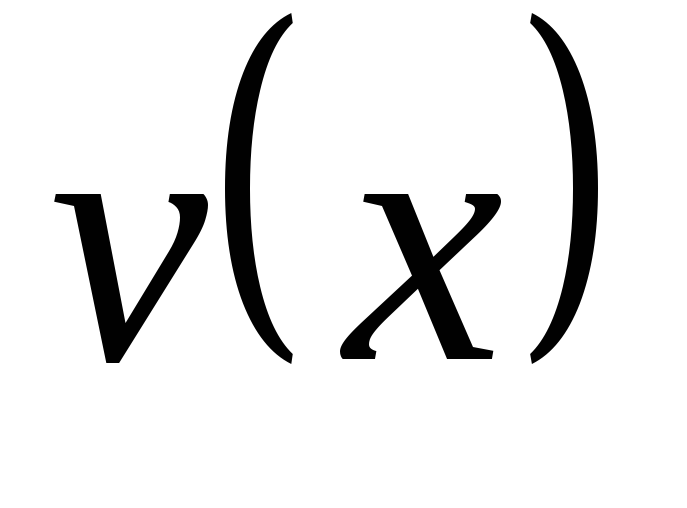 вычисляют последовательным интегрированием
приближенного дифференциального
уравнения (6.5). Проинтегрировав уравнение
(6.5) первый раз, получим выражение для
угла поворота
вычисляют последовательным интегрированием
приближенного дифференциального
уравнения (6.5). Проинтегрировав уравнение
(6.5) первый раз, получим выражение для
угла поворота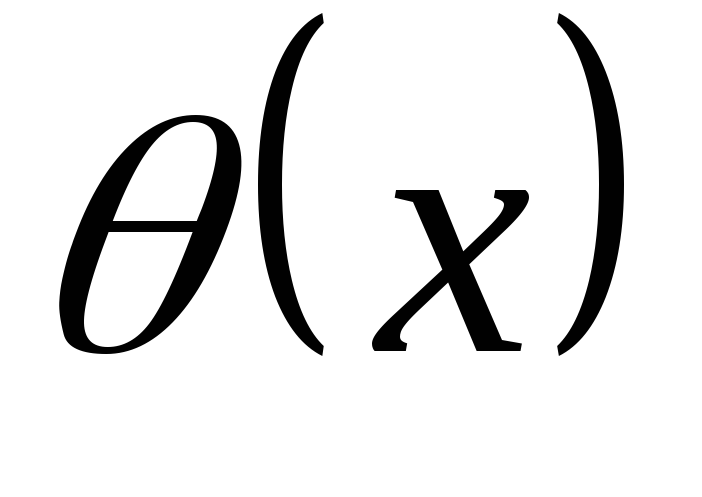 :
:
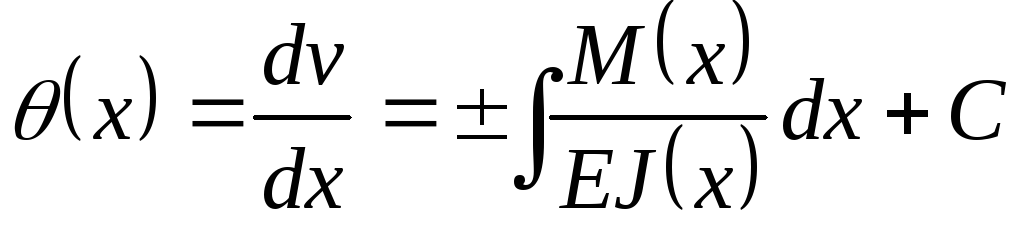 ,
(6.6)
,
(6.6)
где  постоянная интегрирования.
постоянная интегрирования.
Интегрируя
второй раз, получим выражение для прогиба 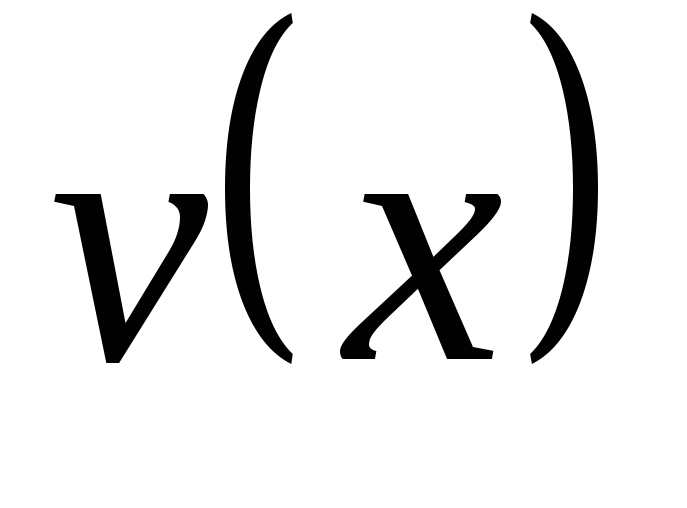 :
:
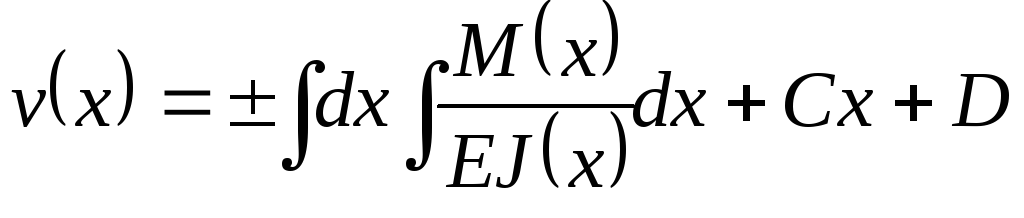 ,
(6.7)
,
(6.7)
где  и постоянные интегрирования.
и постоянные интегрирования.
Для вычисления интегралов, входящих в (6.6) и (6.7), необходимо сначала написать аналитические выражения для изгибающего момента и жесткости. Постоянные интегрирования находятся из граничных условий, которые зависят от условий перемещения границ участков балки.
Рассмотрим несколько примеров применения метода непосредственного интегрирования приближенного уравнения упругой линии балки.
Пример 6.1. Определить стрелу прогиба и угол поворота сечения В балки, изображенной на рис.6.3.

Рис.6.3
Решение:
1. Из условий равновесия определяем опорные реакции:
 ;
;  .
.
2.
Выбираем начало координат 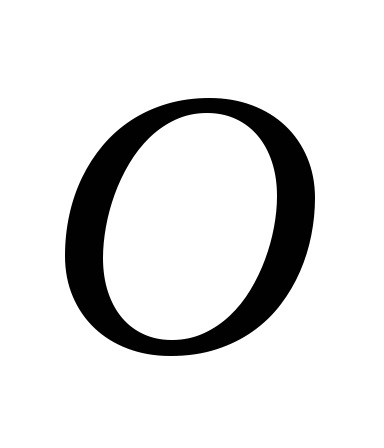 на левом конце балки, совмещая его с
точкой А. Ось
на левом конце балки, совмещая его с
точкой А. Ось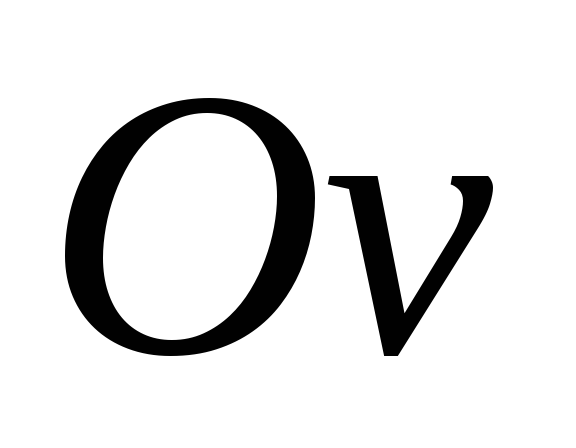 направляем вверх, ось
направляем вверх, ось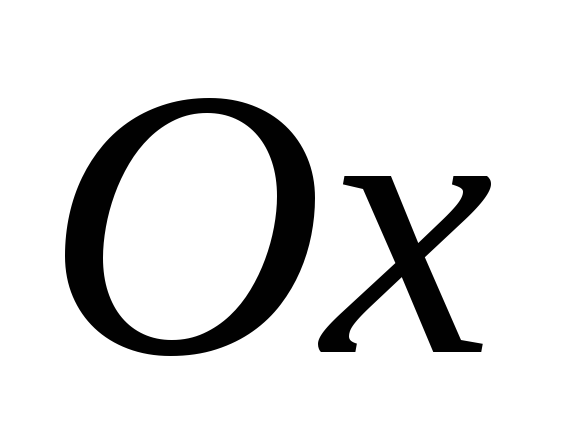 вправо.
вправо.
3.
Составляем уравнение изгибающего
момента в сечении 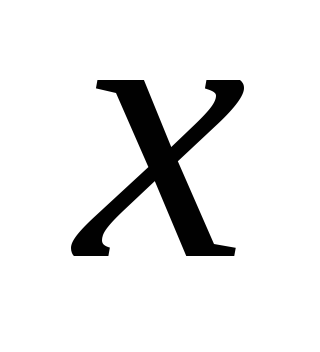 :
:
 .
.
4. Предполагая, что жесткость балки постоянна, записываем приближенное дифференциальное уравнение упругой линии балки:
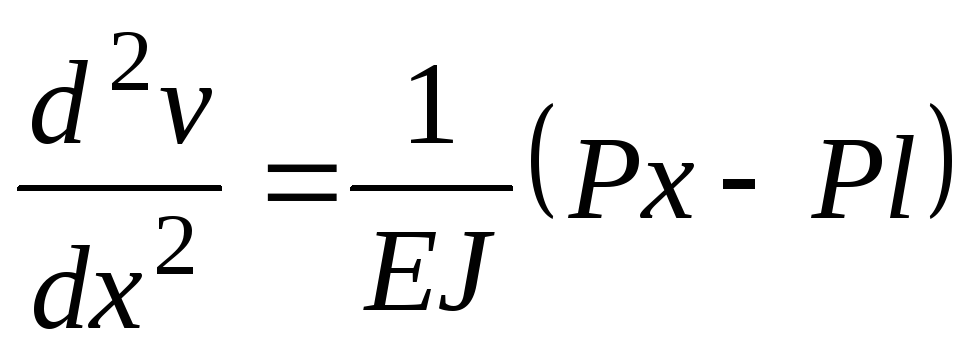 .
.
Знак
“+”
в уравнении упругой лиинии был принят
потому, что ось 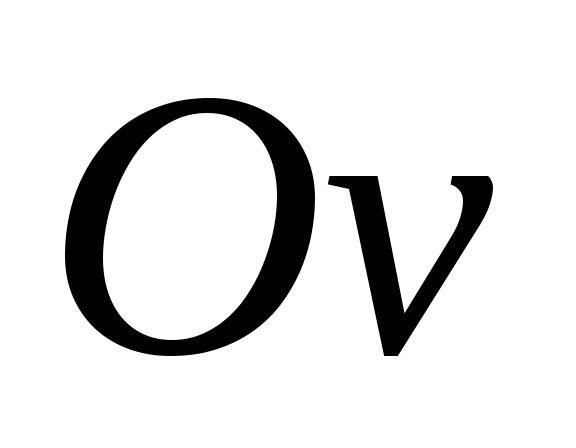 направлена вверх.
направлена вверх.
5. Интегрируем уравнение первый раз. Получаем:
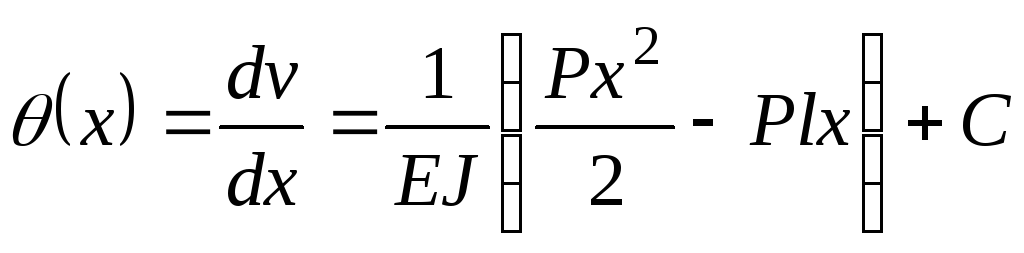 .
(а)
.
(а)
Интегрируя
еще раз, получаем уравнение для прогиба
в сечении 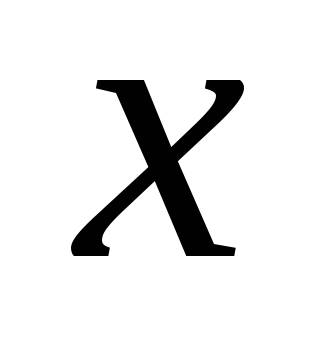 :
:
 .
(б)
.
(б)
Так как в заделке прогиб и угол поворота равны нулю, то для определения постоянных интегрирования граничные условия имеют вид:
при 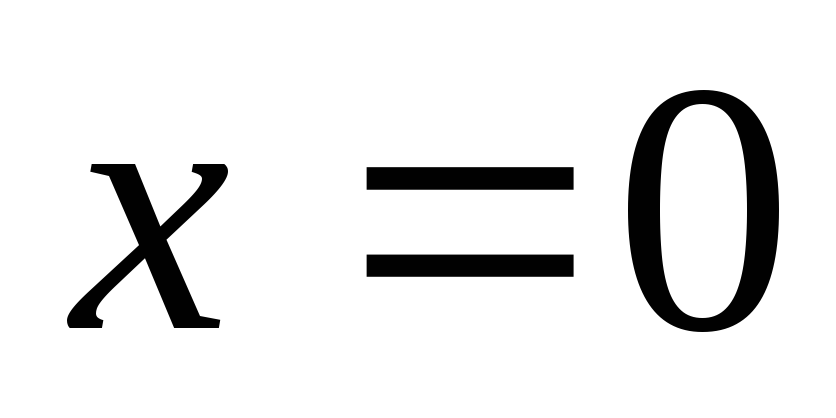
 ;
при
;
при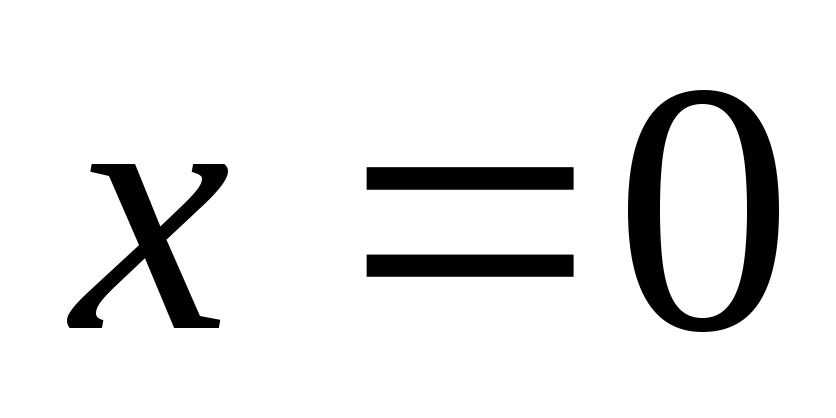
 .
.
Из
уравнения (а) видно, что постоянная  представляет собой угол поворота в
начале координат (сечении А). Задавая в
уравнении (а)
представляет собой угол поворота в
начале координат (сечении А). Задавая в
уравнении (а)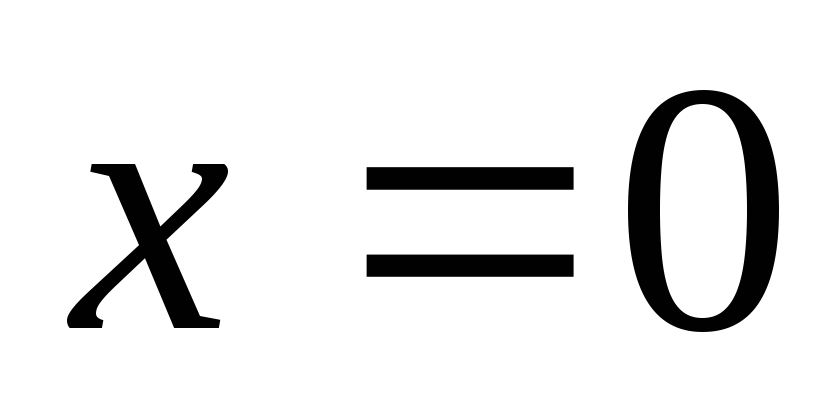 ,
находим
,
находим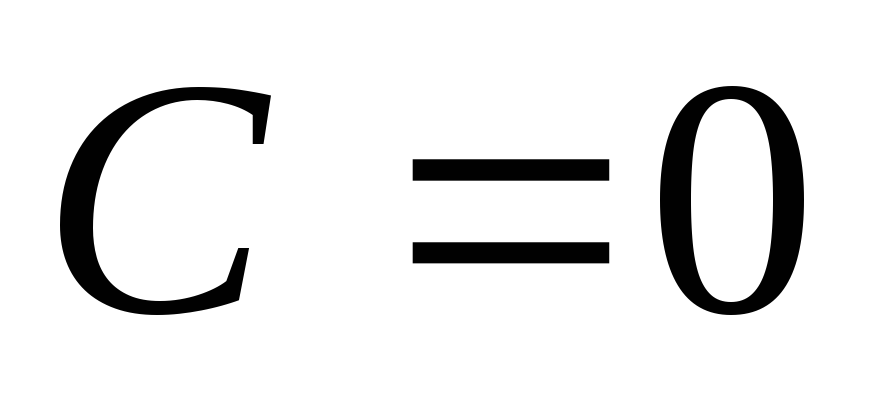 .
Из уравнения (б) следует, что постоянная
.
Из уравнения (б) следует, что постоянная
прогиб в начале координат. Задавая в
уравнении (б)
прогиб в начале координат. Задавая в
уравнении (б) 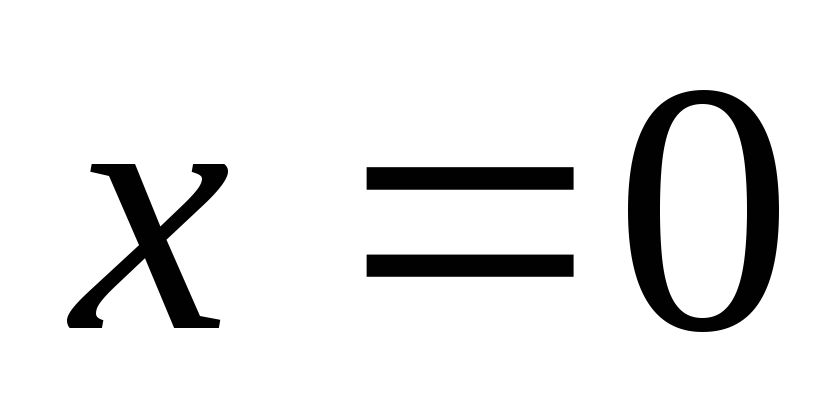 ,
получаем
,
получаем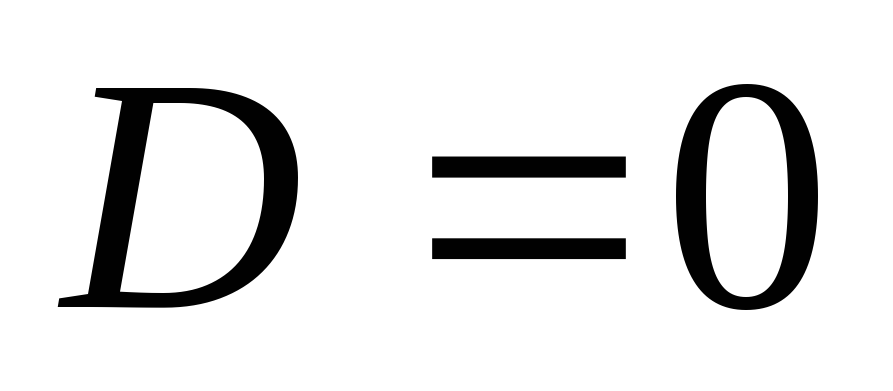 .
.
Таким образом, получаем следующие выражения для прогиба и угла поворота:
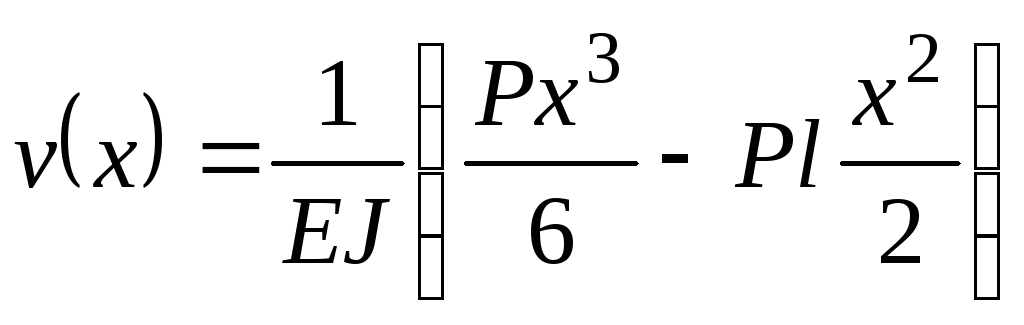 ,
,
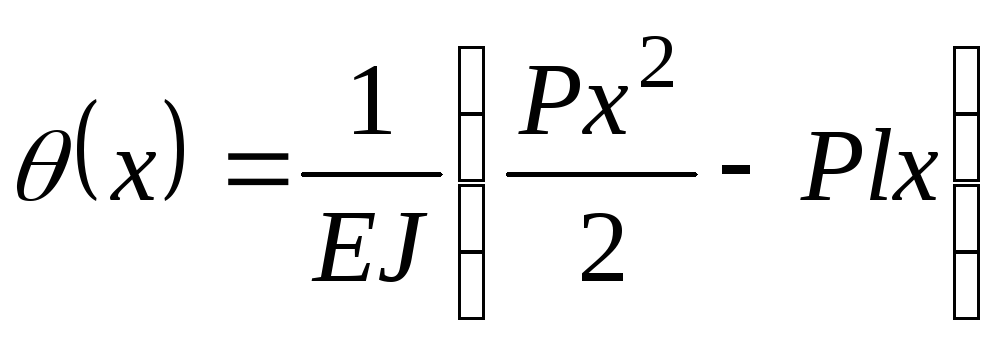 .
.
Подставляя
в первое уравнение 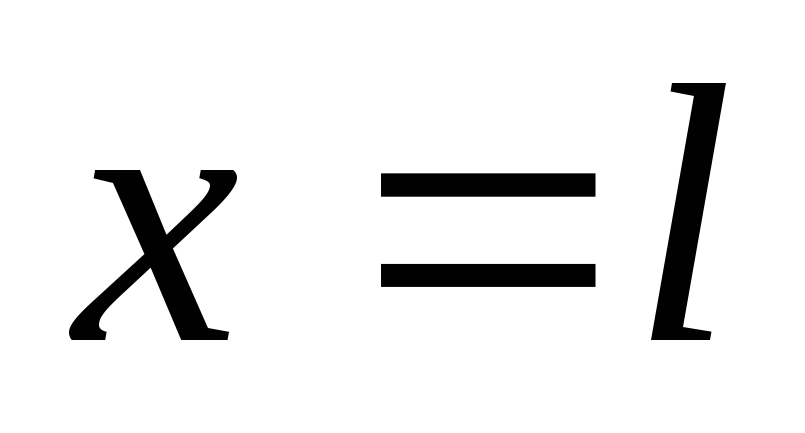 ,
найдем стрелу прогиба:
,
найдем стрелу прогиба:
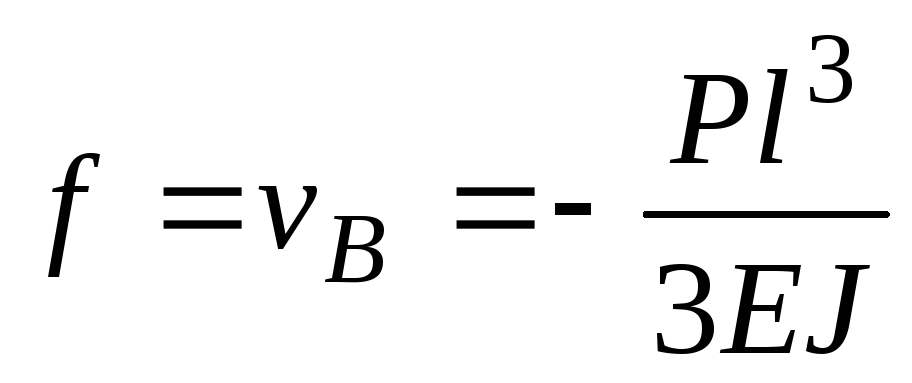 .
.
Подставляя
во второе уравнение 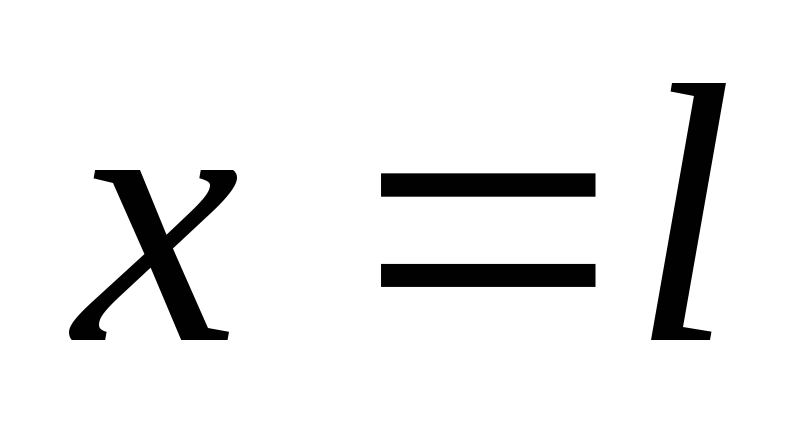 ,
найдем максимальный угол поворота
,
найдем максимальный угол поворота
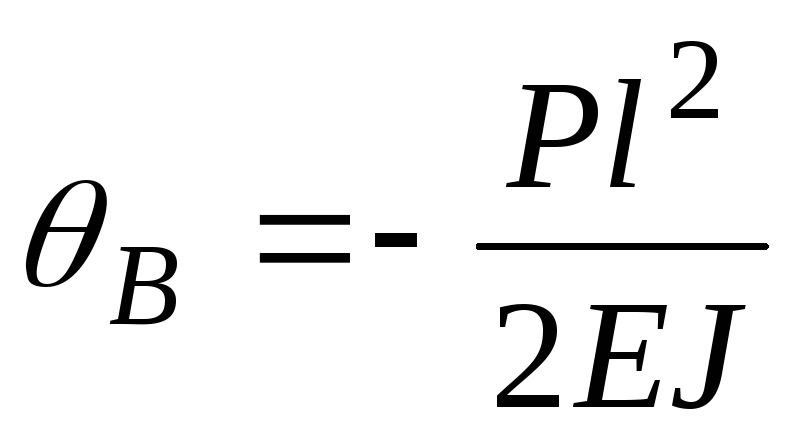 .
.
Знак
“”
у прогиба свидетельствует о том, что
его направление не совпадает с
положительным направлением оси 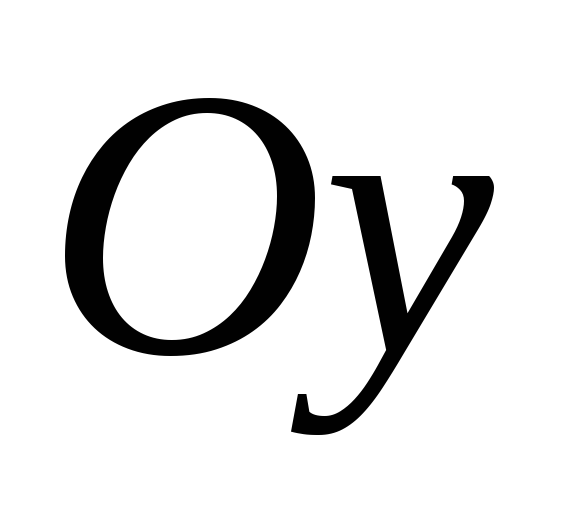 .
Знак“”
в выражении угла поворота показывает,
что сечение В повернулось не против, а
по часовой стрелке.
.
Знак“”
в выражении угла поворота показывает,
что сечение В повернулось не против, а
по часовой стрелке.
Пример 6.2. Определить стрелу прогиба двухопорной балки и углы поворота опорных сечений А и В (рис.6.4).

Рис.6.4
Решение:
1. Из условий равновесия определяем опорные реакции:
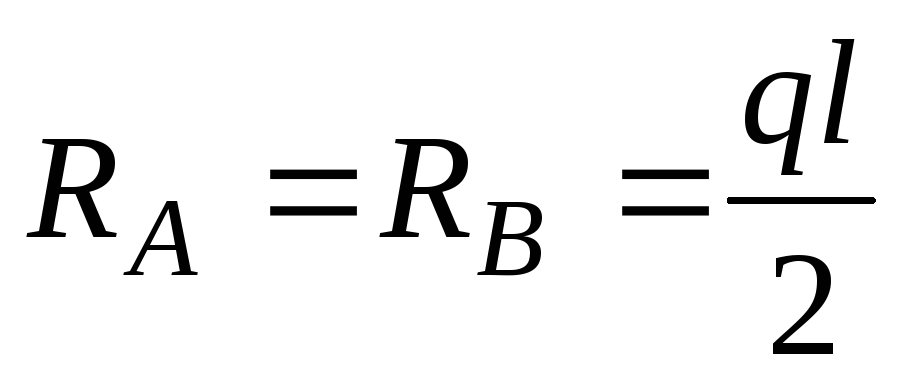 .
.
2.
Выбираем начало координат 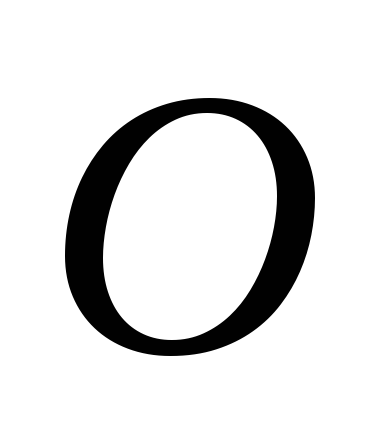 на левом конце балки, совмещая его с
точкой А. Ось
на левом конце балки, совмещая его с
точкой А. Ось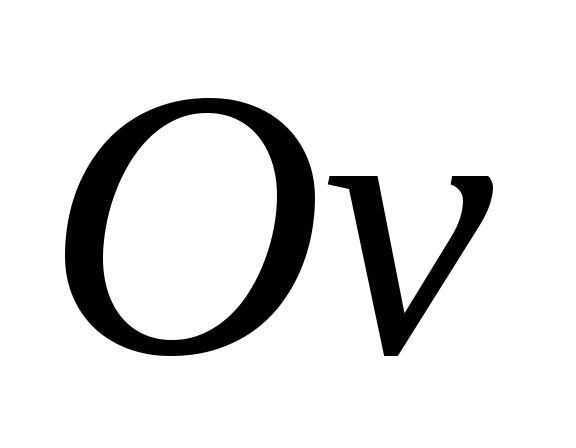 направляем вверх, ось
направляем вверх, ось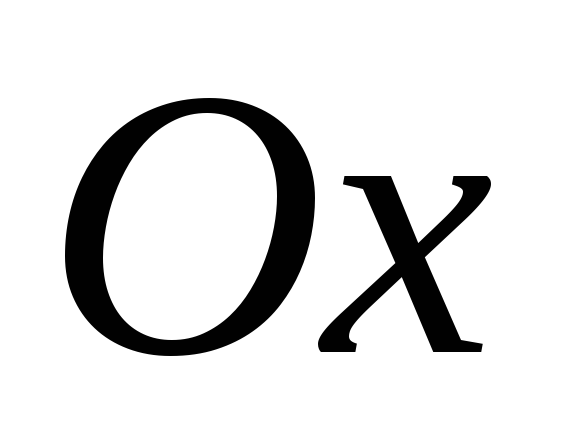
вправо.
вправо.
3.
Составляем уравнение изгибающего
момента в сечении 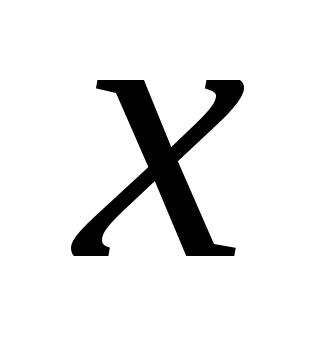 :
:
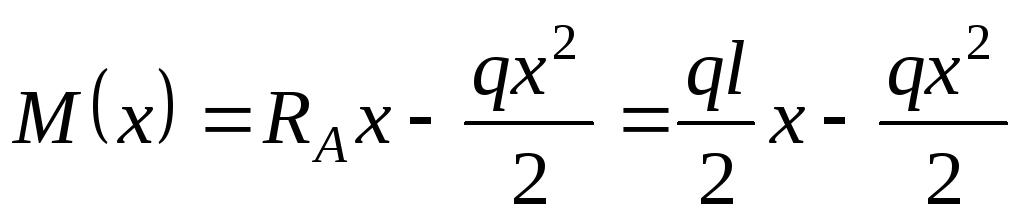 .
.
4. Предполагая, что жесткость балки постоянна, записываем приближенное дифференциальное уравнение упругой линии балки:
 .
.
Знак
“+”
в уравнении упругой лиинии был принят
потому, что ось  направлена вверх.
направлена вверх.
5. Интегрируем уравнение первый раз. Получим:
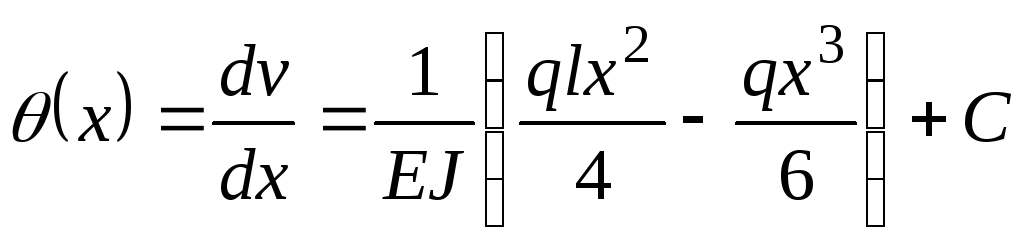 .
(в)
.
(в)
Интегрируя
еще раз, получаем уравнение для прогиба
в сечении  :
:
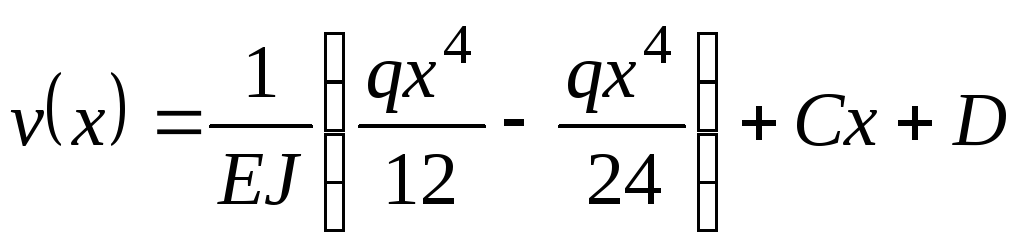 .
(г)
.
(г)
Постоянные интегрирования найдем из граничных условий:
при 
 ;
при
;
при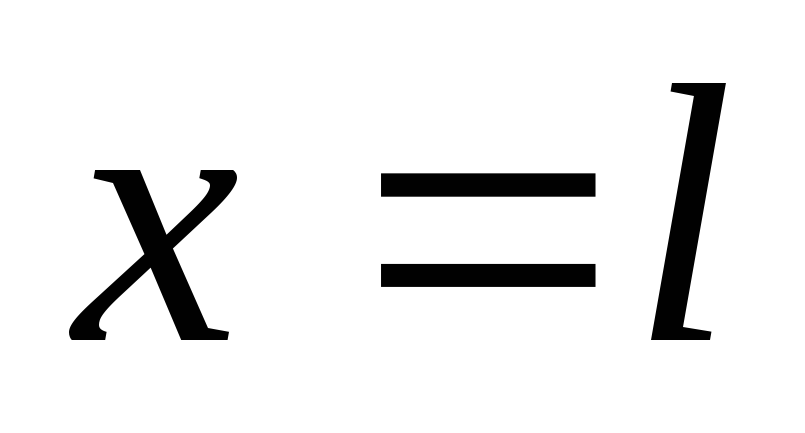
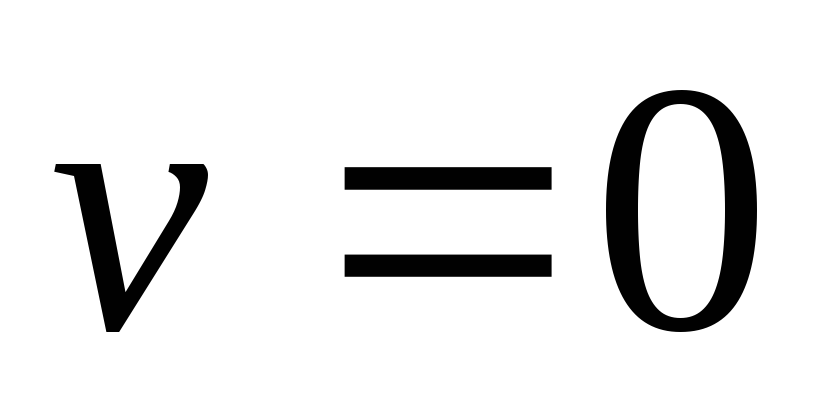 .
.
Подставляя
в уравнение (г) 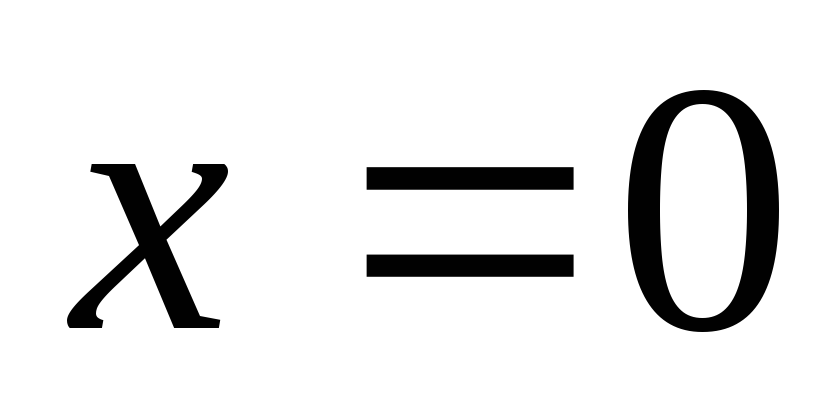 и приравнивая прогиб нулю, получим
и приравнивая прогиб нулю, получим ;
подставляя в это же уравнение
;
подставляя в это же уравнение ,
находим постоянную интегрирования
,
находим постоянную интегрирования :
:
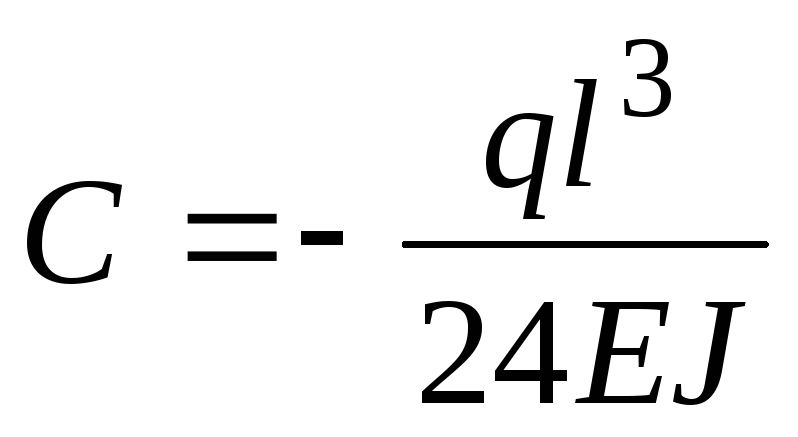 .
.
Найденные значения постоянных интегрирования подставим в уравнения (в) и (г) и получим уравнения углов поворота и прогибов:
 ;
;
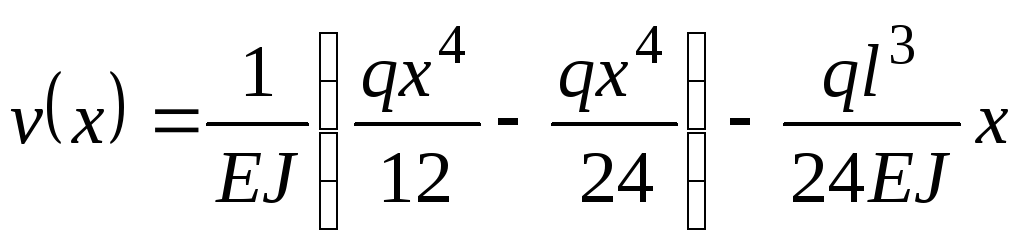 .
.
Подставляя 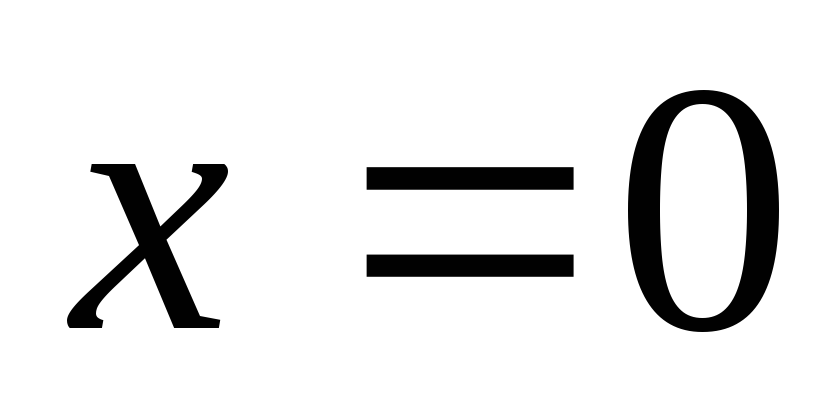 и
и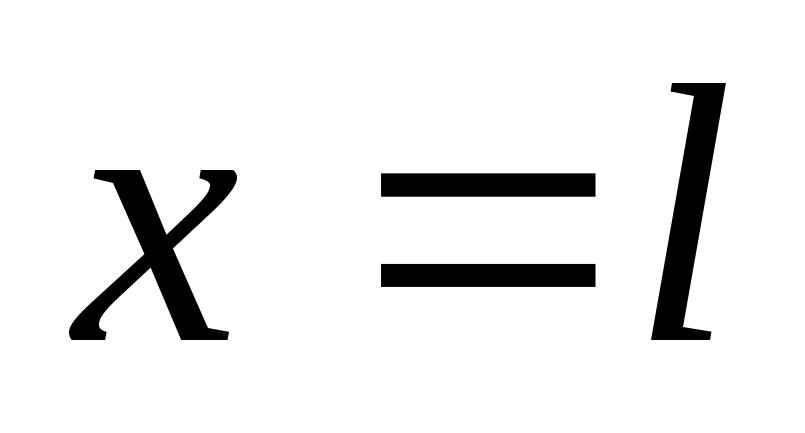 в первое уравнение, получим углы поворота
соответственно сечений А и В:
в первое уравнение, получим углы поворота
соответственно сечений А и В:
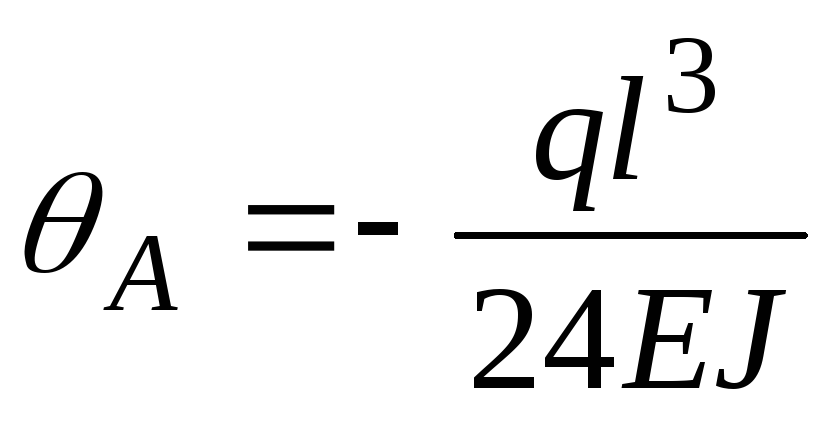 ;
; 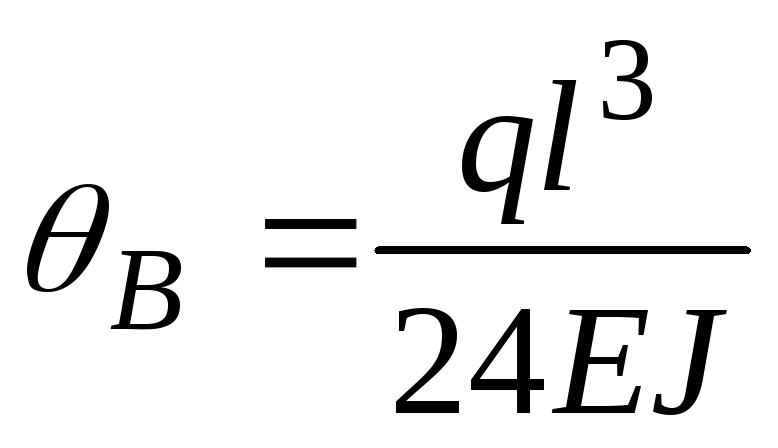 .
.
В
силу симметрии нагрузки максимальный
прогиб
будет посредине балки. Подставляя во
второе уравнение 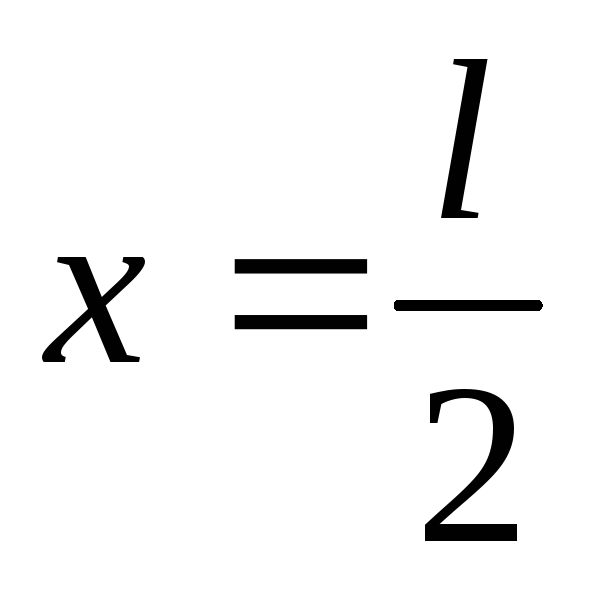 ,
получим:
,
получим:
 .
.
Как
и в предыдущем примере, знак “”
у прогиба свидетельствует о том, что
его направление не совпадает с
положительным направлением оси 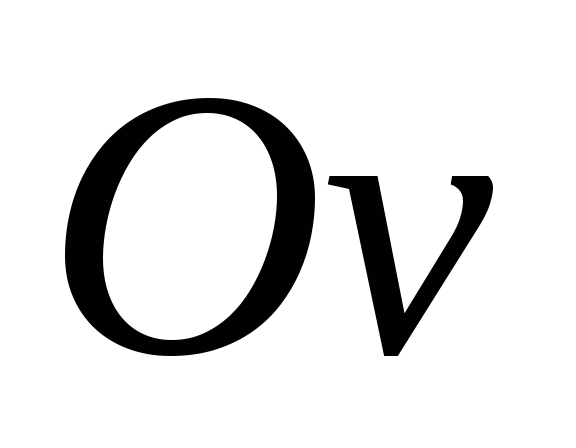 .
Знак“”
в выражении угла поворота
.
Знак“”
в выражении угла поворота  показывает, что сечение А повернулось
не против, а по часовой стрелке, знак“+”
в выражении угла поворота
показывает, что сечение А повернулось
не против, а по часовой стрелке, знак“+”
в выражении угла поворота  показывает, что сечение В повернулось
против часовой стрелки.
показывает, что сечение В повернулось
против часовой стрелки.
Пример 6.3. В сколько раз прогиб в сечении В на конце изображенной на рис.6.5 балки, больше, чем прогиб в сечении С посредине балки?
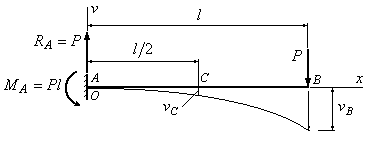
Рис.6.5
Решение:
Воспользуемся результатами, полученными в примере 6.1. Запишем окончательное выражение для прогиба:
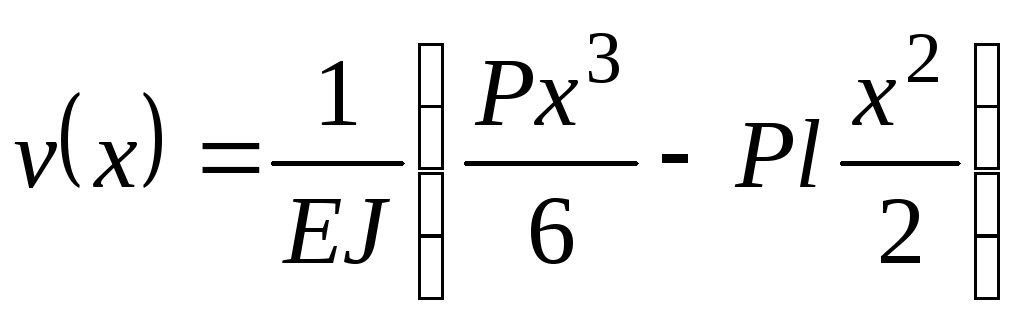
и подставим в это уравнение координаты точек С и В. Получим:
при 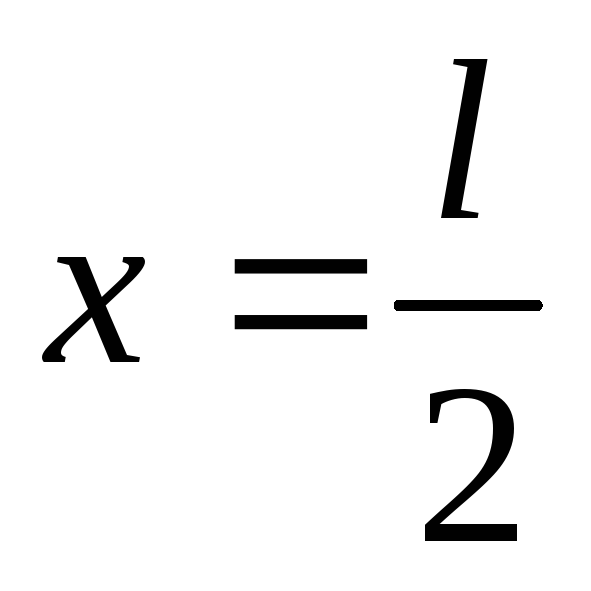
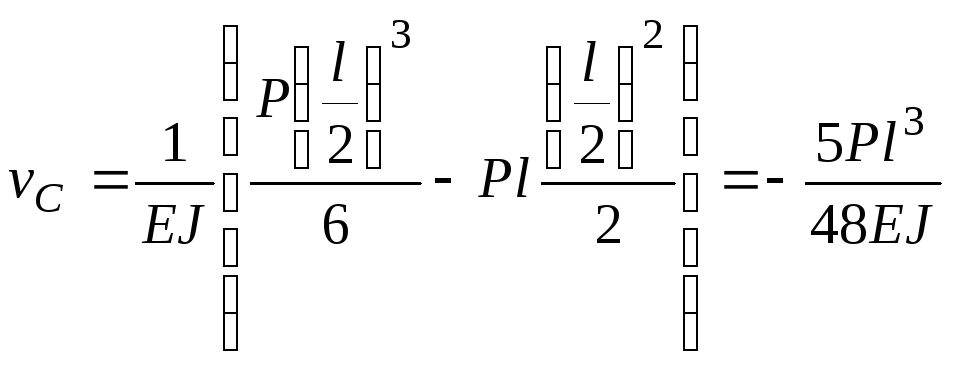 ;
;
при 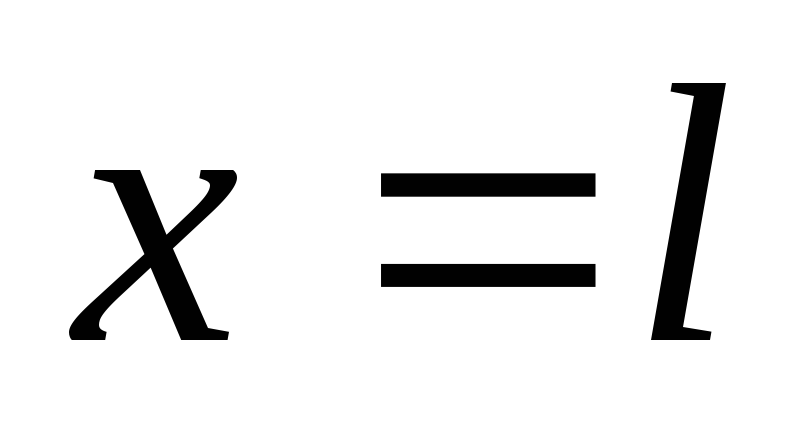
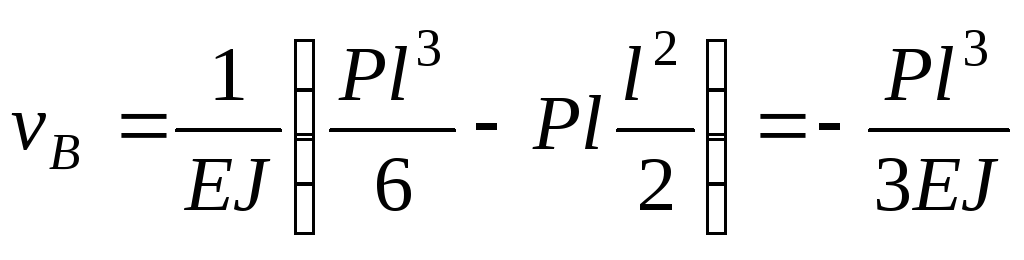 .
.
Сравнивая полученные величины прогибов, приходим к выводу, что прогиб в сечении В больше, чем прогиб в сечении С в 3,2 раза:
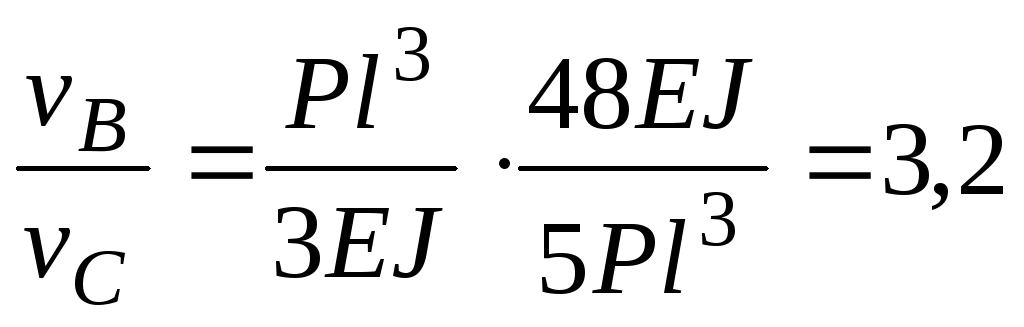 .
.
Пример 6.4. В сколько раз угол поворота сечения А на конце изображенной на рис.6.6 балки больше, чем угол поворота сечения В на расстоянии четверти пролета от левого конца балки?
Решение:
1.
Находим реакции: ;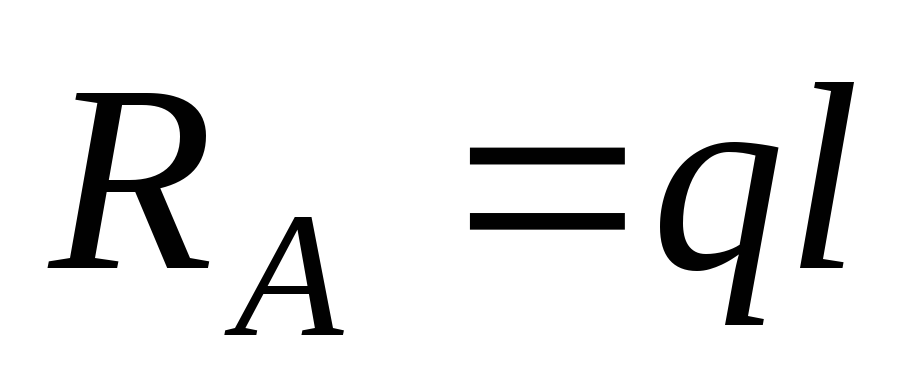 .
.
2.
Выбираем начало координат  на правом конце балки, совмещая его с
точкой А. Ось
на правом конце балки, совмещая его с
точкой А. Ось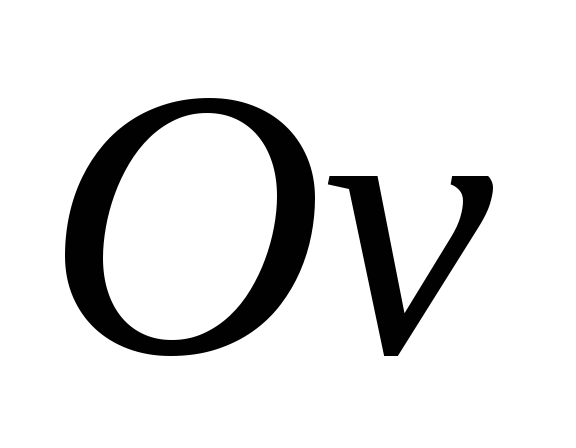 направляем вверх, ось
направляем вверх, ось
влево.
влево.

Рис.6.6
3.
Записываем выражение для изгибающего
момента в сечении 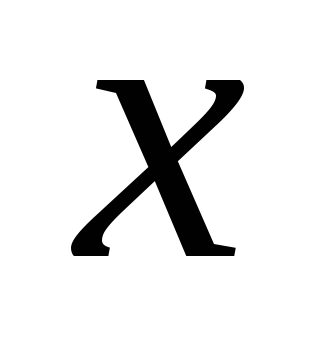 :
:
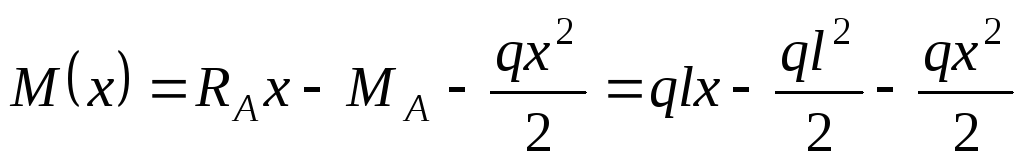 .
.
4. Составляем приближенное дифференциальное уравнение упругой линии балки:
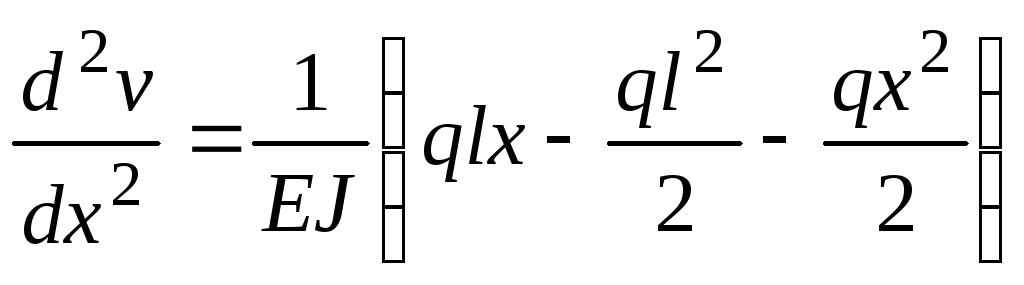 .
.
Знак
“+”
в уравнении упругой лиинии был принят
потому, что ось  направлена вверх.
направлена вверх.
5. Принимаем жесткость балки постоянной. Интегрируем дифференциальное уравнение. Получаем:
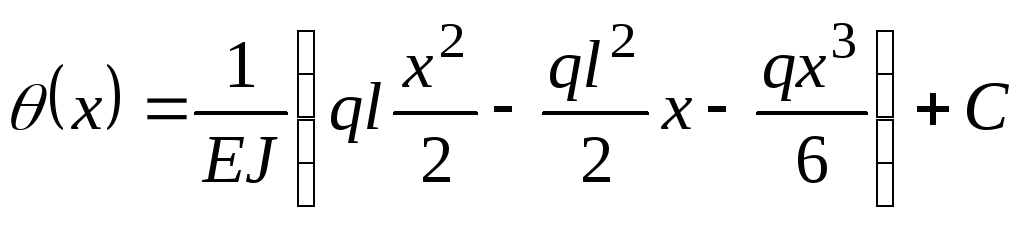 .(д)
.(д)
Постоянную интегрирования  в уравнении (д) найдем из условия, что
при
в уравнении (д) найдем из условия, что
при угол поворота в сечении А равен нулю.
Подставим в уравнение (д)
угол поворота в сечении А равен нулю.
Подставим в уравнение (д)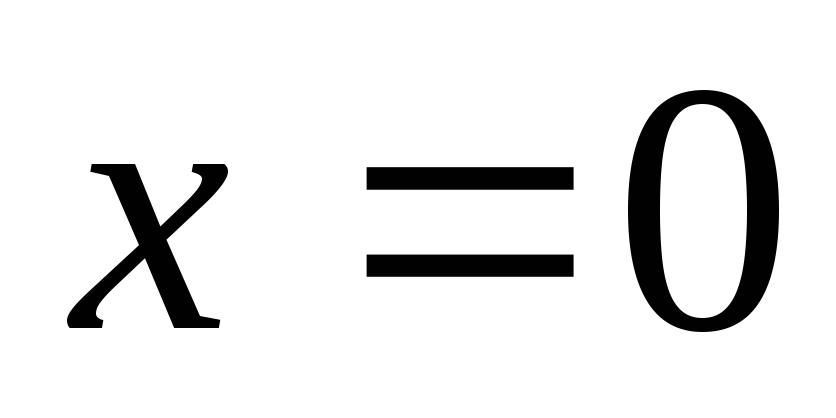 и приравняем нулю угол поворота сечения
А. Получим
и приравняем нулю угол поворота сечения
А. Получим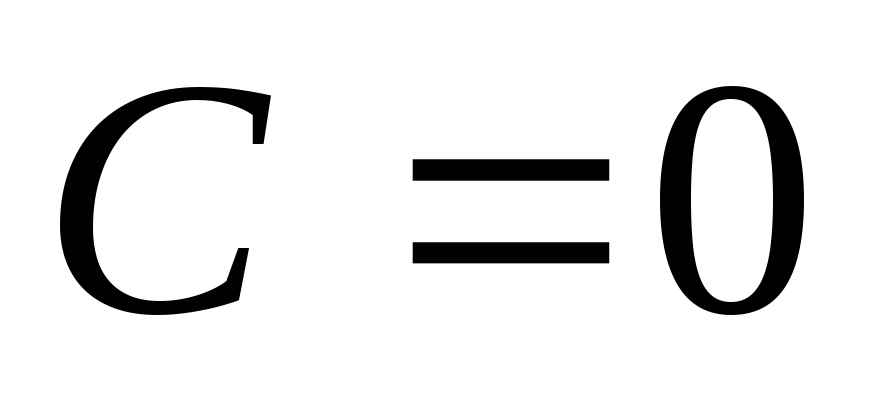 .
Тогда окончательно уравнение для угла
поворота принимает вид:
.
Тогда окончательно уравнение для угла
поворота принимает вид:
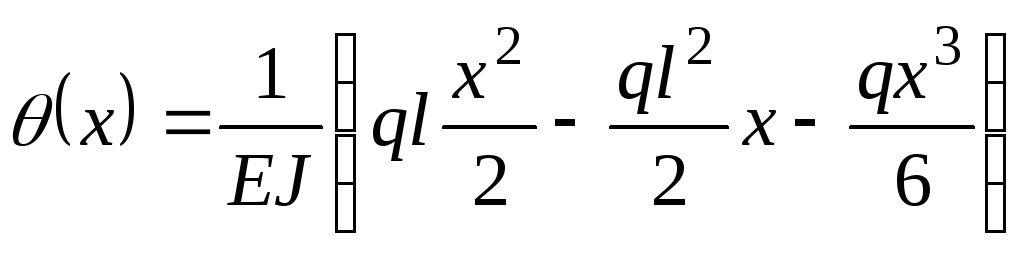 .(е)
.(е)
6.
Подставляем в уравнение (е) координату 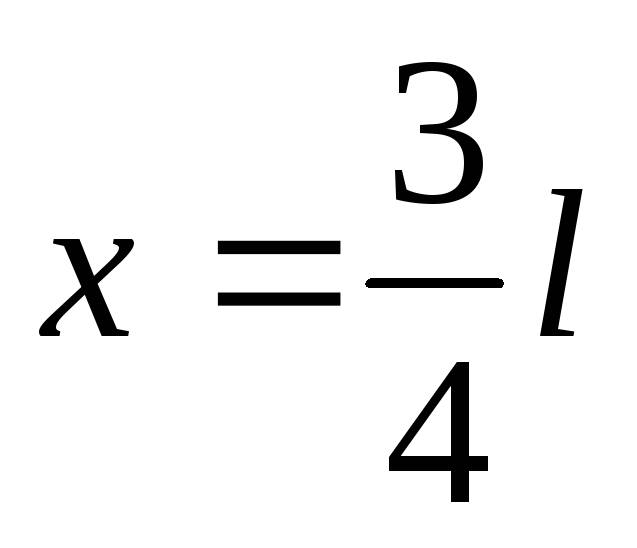 ,
получим угол поворота в сечении С:
,
получим угол поворота в сечении С:
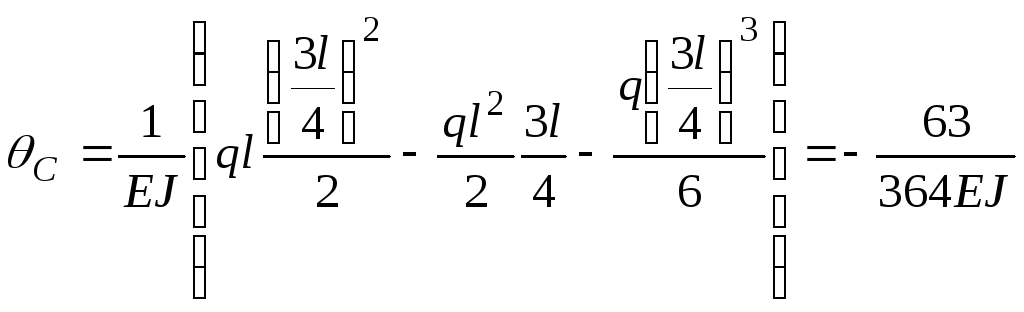 .
.
7.
Подставляем в уравнение (е) координату 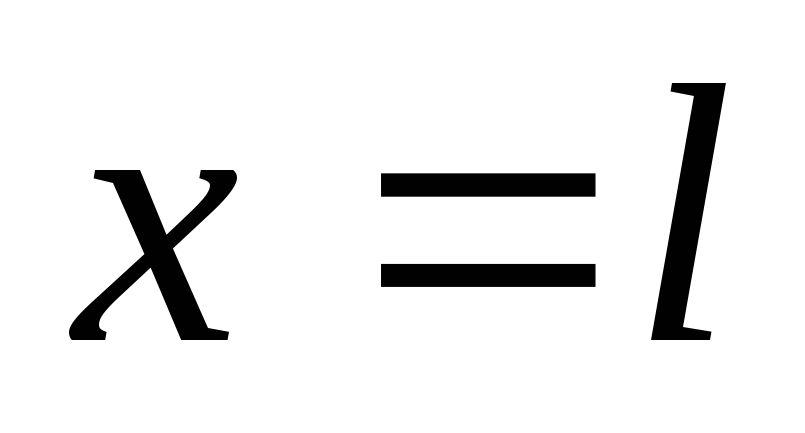 .
Получим угол поворота в сечении В:
.
Получим угол поворота в сечении В:
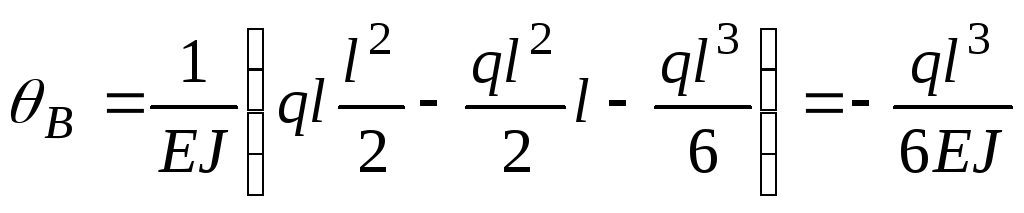 .
.
8. Сравнивая углы поворота в сечениях В и С, получим:
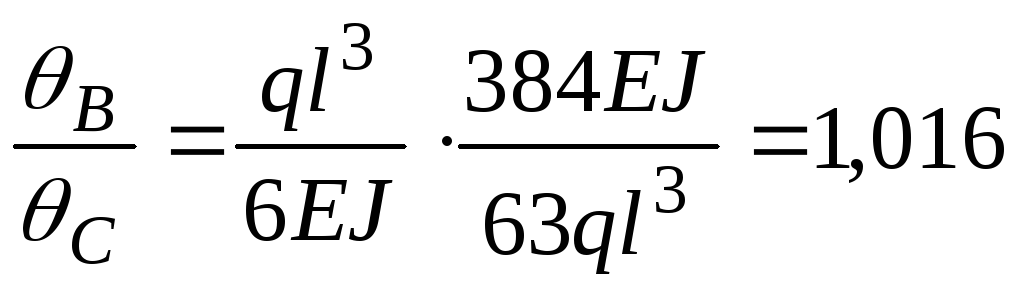 .
.
Таким образом, угол поворота в сечении В в 1,016 раза больше, чем угол поворота в сечении С.
Пример
6.5. Найти
стрелу прогиба (в мм) балки, изображенной
на рис.6.7, если жесткость поперечного
сечения балки равна  кНм2.
кНм2.

Рис.6.7
Решение:
Воспользуемся
решение задачи, ход которого изложен в
примере 6.4 и проинтегрируем выражение
(д). Получим уравнение для прогиба в
сечении 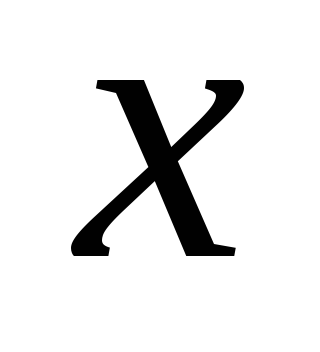 :
:
 .
(ж)
.
(ж)
Постоянные интегрирования в уравнении (ж) получим, воспользовавшись граничными усорвиями закрепления балки, в соответствии с которыми прогиб и угол поворота в жесткой заделке равны нулю:
при 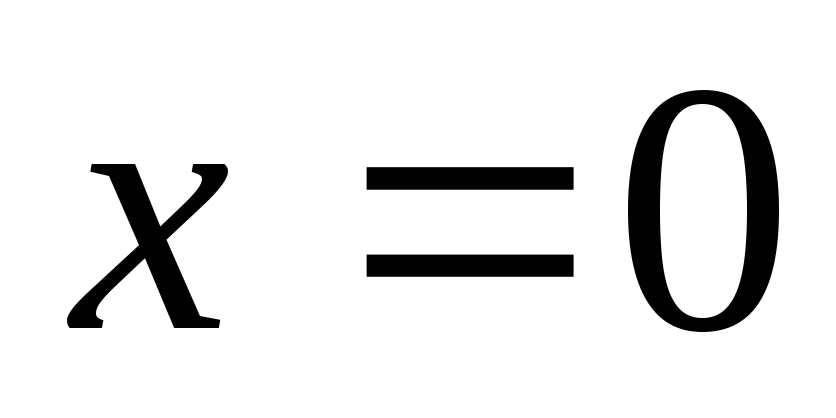
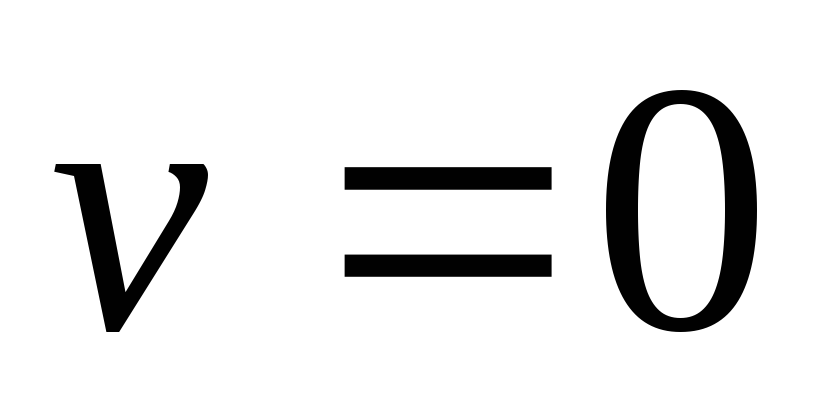 и
и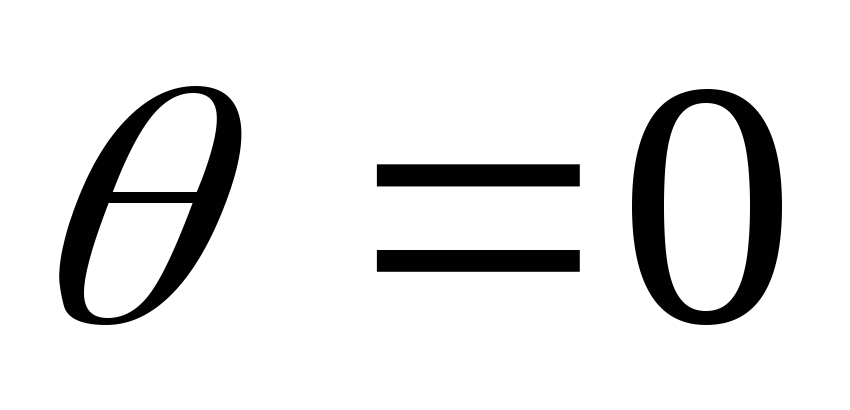 .
.
Подставляя 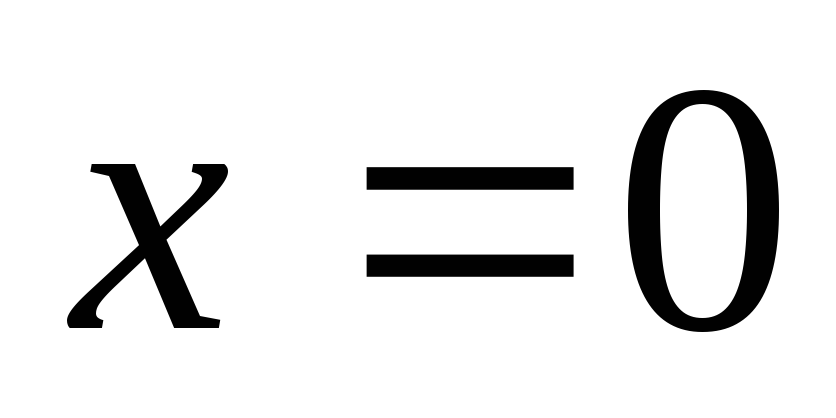 в уравнения (д) и (ж) и приравнивая
последовательно нулю угол поворота и
прогиб нулю, получим:
в уравнения (д) и (ж) и приравнивая
последовательно нулю угол поворота и
прогиб нулю, получим: ;
;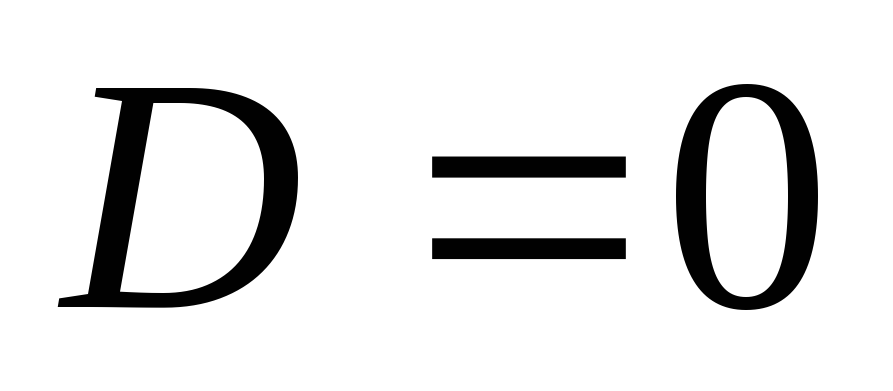 .
Тогда выражение для прогиба принимает
вид:
.
Тогда выражение для прогиба принимает
вид:
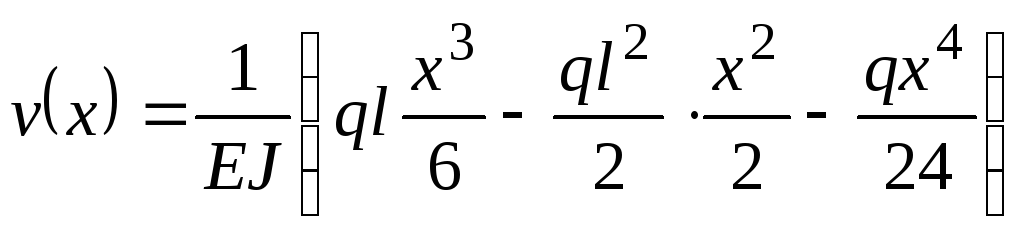 .
.
Подставляя
в это уравнение заданные значения
жесткости сечения, интенсивности
распределенной нагрузки, длину балки,
а также координату сечения В, в котором
определяется стрела прогиба ( ),
находим:
),
находим:
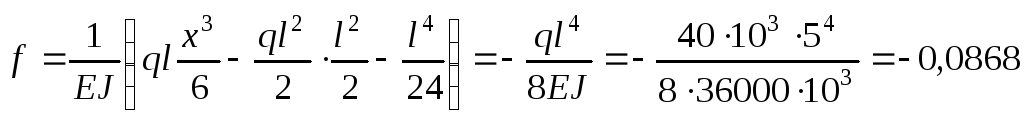 м
м мм.
мм.
Знак
“”
у прогиба свидетельствует о том, что
его направление не совпадает с
положительным направлением оси  .
.
Определение прогибов углов поворота (сопромат)

Определение прогибов и углов поворота поперечного сечения балки определяют с помощью универсального уравнения изогнутой оси балки (универсального уравнения упругой линии балки)
Формула (закон изменения) прогиба балки в сечении с координатой z и угол поворота сечения (рис. 7.15):
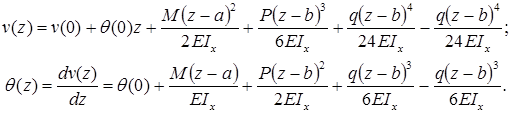
a и b – абсциссы точек приложения сосредоточенного момента M и сосредоточенной силы P, соответственно; c и d – координаты начала и конца участка, нагруженного распределенной нагрузкой.
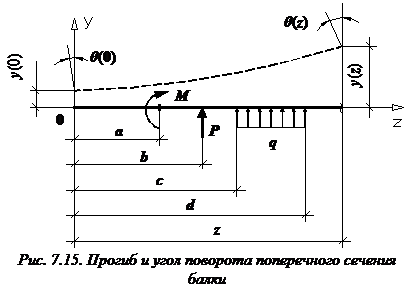
В формулы входят только внешние усилия, которые расположены левее сечения, в котором определяются перемещения балки.
Если какая-нибудь нагрузка имеет противоположное указанному на рисунке 7.15 направление, то у соответствующих слагаемых в формулах прогибов и углов поворота сечений следует поменять знак на противоположный.
Прогиб 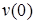 и угол поворота
и угол поворота 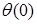 балки в начале координат (начальные параметры) определяются из условий закрепления балки.
балки в начале координат (начальные параметры) определяются из условий закрепления балки.
Уравнение упругой линии балки на примере
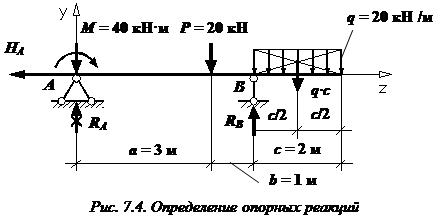
Определим прогиб балки на консоли при 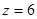 м, то есть
м, то есть 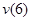 . Запишем универсальное уравнение упругой линии балки:
. Запишем универсальное уравнение упругой линии балки:
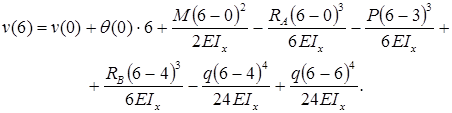
Прогиб балки в начале координат (на левой шарнирной опоре), равен нулю: 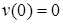 .
.
Для определения угла поворота в начале координат необходимо составить дополнительное условие: прогиб на правой опоре равен нулю.
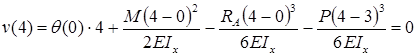 ,
,
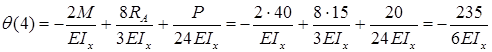 .
.
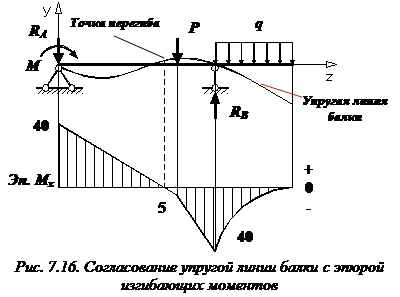
Прогиб консоли при z=6м:
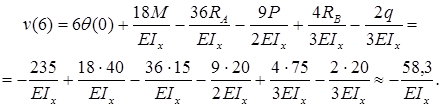
Знак «минус» говорит: прогиб балки на консоли происходит вниз. Число, стоящее в числителе, измеряется в килоньютонах на метр в кубе (кН·м3).
Примерный вид упругой линии балки показан на рис. 7.16.
Упругая линия балки должна быть согласована с эпюрой изгибающих моментов по дифференциальным зависимостям. Точка перегиба находится под сечением балки, в котором изгибающий момент равен нулю, что следует из закона Гука при изгибе.
