Длина высота широта – Географическая широта и географическая долгота. Географические координаты

Содержание

Географические координаты — Википедия

У этого термина существуют и другие значения, см. Координаты.

Географи́ческие координа́ты — обобщённое понятие о геодезических и астрономических координатах, когда уклонение отвесной линии не учитывают^[1]. Иными словами, при определении географических координат Земля принимается за шар. Географические координаты определяют положение точки на земной поверхности или, более широко, в географической оболочке. Географические координаты строятся по принципу сферических. Аналогичные координаты применяются для других планет, а также на небесной сфере^[2].

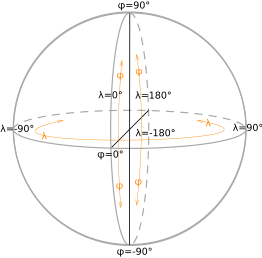
Широта́ — угол φ между местным направлением зенита и плоскостью экватора, отсчитываемый от 0° до 90° в обе стороны от экватора. Географическую широту точек, лежащих в северном полушарии, (северную широту) принято считать положительной, широту точек в южном полушарии — отрицательной. О широтах, близких к полюсам, принято говорить как о

высоких, а о близких к экватору — как о низких.

Из-за отличия формы Земли от шара, географическая широта точек несколько отличается от их геоцентрической широты, то есть от угла между направлением на данную точку из центра Земли и плоскостью экватора.

Широту места можно определить с помощью таких астрономических инструментов, как секстант или гномон (прямое измерение), также можно воспользоваться системами GPS или ГЛОНАСС (косвенное измерение).

Долгота́ — двугранный угол λ между плоскостью меридиана, проходящего через данную точку, и плоскостью начального нулевого меридиана, от которого ведётся отсчёт долготы. Долготу от 0° до 180° к востоку от нулевого меридиана называют восточной, к западу — западной. Восточные долготы принято считать положительными, западные — отрицательными.

Выбор нулевого меридиана произволен и зависит только от соглашения. Сейчас за нулевой меридиан принят Опорный меридиан, проходящий рядом с обсерваторией в Гринвиче, на юго-востоке Лондона. В качестве нулевого ранее выбирались меридианы обсерваторий Парижа, Кадиса, Пулкова и т. д.

От долготы зависит местное солнечное время.

Чтобы полностью определить положение точки трёхмерного пространства, необходима третья координата — высота. Расстояние до центра планеты не используется в географии: оно удобно лишь при описании очень глубоких областей планеты или, напротив, при расчёте орбит в космосе.

В пределах географической оболочки применяется обычно высота над уровнем моря, отсчитываемая от уровня «сглаженной» поверхности — геоида. Такая система трёх координат оказывается ортогональной, что упрощает ряд вычислений. Высота над уровнем моря удобна ещё тем, что связана с атмосферным давлением.

Расстояние от земной поверхности (ввысь или вглубь) часто используется для описания места, однако ‘не’ служит координатой.

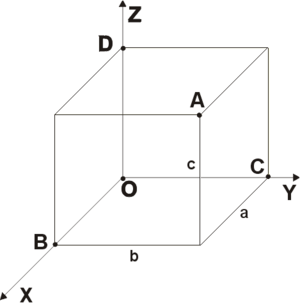
В навигации в качестве начала системы координат выбирается центр масс транспортного средства (ТС). Переход начала координат из инерциальной системы координат в географическую (то есть из Oi{\displaystyle O_{i}} в Og{\displaystyle O_{g}}) осуществляется исходя из значений широты и долготы. Координаты центра географической системы координат Og{\displaystyle O_{g}} в инерциальной принимают значения (при расчёте по шарообразной модели Земли):

Xog=(R+h)cos⁡(φ)cos⁡(Ut+λ){\displaystyle X_{og}=(R+h)\cos(\varphi )\cos(Ut+\lambda )}

Yog=(R+h)cos⁡(φ)sin⁡(Ut+λ){\displaystyle Y_{og}=(R+h)\cos(\varphi )\sin(Ut+\lambda )}

Zog=(R+h)sin⁡(φ){\displaystyle Z_{og}=(R+h)\sin(\varphi )}

где R — радиус земли , U — угловая скорость вращения Земли, h — высота над уровнем моря, φ{\displaystyle \varphi } — широта, λ{\displaystyle \lambda } — долгота, t — время.

Ориентация осей в географической системе координат (Г. С. К.) выбирается по схеме:

Ось X (другое обозначение — ось E) — ось, направленная на восток.

Ось Y (другое обозначение — ось N) — ось, направленная на север.

Ось Z (другое обозначение — ось Up) — ось, направленная вертикально вверх.

Ориентация трёхгранника XYZ,из-за вращения земли и движения Т. С. постоянно смещается с угловыми скоростями^[3].

ωE=−VN/R{\displaystyle \omega _{E}=-V_{N}/R}

ωN=VE/R+Ucos⁡(φ){\displaystyle \omega _{N}=V_{E}/R+U\cos(\varphi )}

ωUp=VERtg(φ)+Usin⁡(φ){\displaystyle \omega _{Up}={\frac {V_{E}}{R}}tg(\varphi )+U\sin(\varphi )}

где R — радиус земли , U — угловая скорость вращения Земли, VN{\displaystyle V_{N}} — скорость транспортного средства на север, VE{\displaystyle V_{E}} — на восток, φ{\displaystyle \varphi } — широта, λ{\displaystyle \lambda } — долгота.

Основным недостатком в практическом применении Г. С. К. в навигации является большие величины угловой скорости этой системы в высоких широтах, возрастающие вплоть до бесконечности на полюсе. Поэтому вместо Г. С. К. используется полусвободная в азимуте СК.

Полусвободная в азимуте система координат[править | править код]

Полусвободная в азимуте С. К. отличается от Г. С. К. только одним уравнением, которое имеет вид:

ωUp=Usin⁡(φ){\displaystyle \omega _{Up}=U\sin(\varphi )}

Соответственно, система имеет тоже начальное положение, осуществляется по формуле^[3]

N=Ywcos⁡(ε)+Xwsin⁡(ε){\displaystyle N=Y_{w}\cos(\varepsilon )+X_{w}\sin(\varepsilon )}

E=−Ywsin⁡(ε)+Xwcos⁡(ε){\displaystyle E=-Y_{w}\sin(\varepsilon )+X_{w}\cos(\varepsilon )}

В реальности все расчёты ведутся именно в этой системе, а потом, для выдачи выходной информации происходит преобразование координат в ГСК.

Форматы записи географических координат[править | править код]

Для записи географических координат может использоваться любой эллипсоид (или геоид), но чаще всего используются WGS 84 и Красовского (на территории РФ).

Координаты (широта от −90° до +90°, долгота от −180° до +180°) могут записываться:

Разделителем десятичной дроби может служить точка или запятая. Положительные знаки координат представляются (в большинстве случаев опускаемым) знаком «+» либо буквами:

«N» или «с. ш.» — северная широта,

«E» или «в. д.» — восточная долгота.

Отрицательные знаки координат представляются либо знаком «−», либо буквами:

«S» или «ю. ш.» — южная широта,
«W» или «з. д.» — западная долгота.

Буквы могут стоять как впереди, так и сзади. Единых правил записи координат не существует.

На картах поисковых систем по умолчанию показываются координаты в градусах с десятичной дробью со знаком «−» для отрицательной долготы. На картах Google и картах Яндекс вначале широта, затем долгота (до октября 2012 на картах Яндекс был принят обратный порядок: сначала долгота, потом широта). Эти координаты видны, например, при прокладке маршрутов от произвольных точек. При поиске распознаются и другие форматы.

В то же время часто используется и исконный способ записи с градусами, минутами и секундами. В настоящее время координаты могут записываться одним из множества способов или дублироваться двумя основными (с градусами и с градусами, минутами и секундами)

[4]. Как пример, варианты записи координат знака «Нулевой километр автодорог Российской Федерации» — 55°45′21″ с. ш. 37°37′04″ в. д.^HGЯOL:

55,755831°, 37,617673° — градусы
N55.755831°, E37.617673° — градусы (+ доп. буквы)
55°45.35′N, 37°37.06′E — градусы и минуты (+ доп. буквы)
55°45′20.9916″N, 37°37′3.6228″E — градусы, минуты и секунды (+ доп. буквы)

При необходимости форматы можно пересчитать самостоятельно: 1° = 60′ (минутам), 1′ (минута) = 60″ (секундам). Также можно использовать специализированные сервисы. См. ссылки.

Широта — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 6 марта 2018; проверки требуют 7 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 6 марта 2018; проверки требуют 7 правок.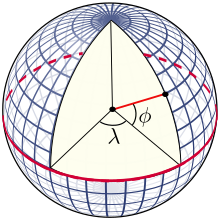

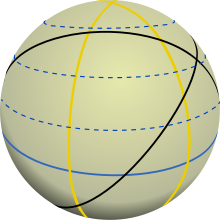Широта (φ) и долгота (λ) на сфере.

Экватор (синий) делит шар пополам и пересекает меридианы (жёлтый) под углом 90°. Все сплошные линии этого рисунка — ортодромии. Пунктирные линии — параллели (все точки такой линии имеют одинаковую широту)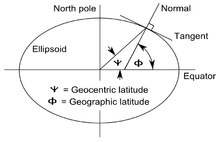

Различие между геодезической широтой (φ) и геоцентрической (ψ)

Широта́ — координата в ряде систем сферических координат, определяющая положение точек на поверхности Земли и других небесных тел, а также на небесной сфере (см. эклиптическая широта, галактическая широта)^[1].

Широту принято отсчитывать от экватора на север. Таким образом, широта точек, лежащих в северном полушарии, положительна, а в южном — отрицательна. Широта любой точки экватора равна 0°, северного полюса — +90°, южного полюса — −90°

[1]. У всех точек одной параллели широта одинакова. Широты, близкие к экватору, называют «низкими», а близкие к полюсам — «высокими».

Широту на поверхности Земли можно определять разными способами с немного различным результатом^[1]:

астрономическая широта ϕ{\displaystyle \phi } — угол между отвесной линией (перпендикуляром к геоиду) и плоскостью экватора Земли. Равна угловой высоте полюса мира. Определяется с помощью астрономических наблюдений;
геодезическая широта ϕs{\displaystyle \phi _{s}} — угол между перпендикуляром к эллипсоиду, приблизительно описывающему форму Земли (земному эллипсоиду), и плоскостью экватора этого эллипсоида. Рассчитывается по измерениям, сделанным на земной поверхности;
геоцентрическая широта ϕg{\displaystyle \phi _{g}} — угол между радиусом, проведённым из центра земного эллипсоида, и плоскостью его экватора^[1]. Отличается от геодезической широты из-за отличия земного эллипсоида от сферы.

Различия этих величин небольшие. Разница геодезической и геоцентрической широты ϕs−ϕg{\displaystyle \phi _{s}-\phi _{g}} достигает максимума (около 12′) при ϕg=45∘{\displaystyle \phi _{g}=45^{\circ }}; на экваторе и полюсах она равна нулю^[1]^[2].

Широту места можно определить с помощью таких астрономических инструментов как секстант или гномон (прямое измерение), также можно воспользоваться системами GPS или ГЛОНАСС (косвенное измерение). От широты, как и от времени года, зависит продолжительность дня.

Географическая широта и географическая долгота. Географические координаты

Видеоурок «Географическая широта и географическая долгота. Географические координаты» поможет вам получить представление о географической широте и географической долготе. Учитель расскажет, как правильно определять географические координаты.

Цель урока: определить понятия «географическая широта», «географическая долгота» и научиться определять географические координаты.

Географическую широту определяют с помощью параллелей. Широта может быть северной (те параллели, которые находятся севернее экватора) и южной (те параллели, которые лежат южнее экватора). Значение широт измеряется в градусах и минутах. Географическая широта может иметь значения от 0 до 90 градусов.

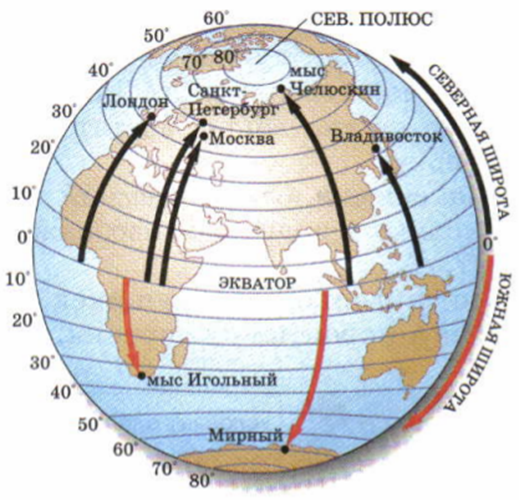
Рис. 1. Определение широт (Источник)

Географическая широта – длина дуги в градусах от экватора до заданной точки.

Чтобы определить широту объекта, надо найти параллель, на которой находится этот объект.

Например, широта Москвы – 55 градусов и 45 минут северной широты, записывается это так: Москвы 55°45′ с.ш.; широта Нью-Йорка – 40°43′ с.ш.; Сидней – 33°52′ ю.ш.

Географическую долготу определяют по меридианам. Долгота может быть западной (от 0 меридиана на запад до 180 меридиана) и восточной (от 0 меридиана на восток до 180 меридиана). Значение долгот измеряется в градусах и минутах. Географическая долгота может иметь значения от 0 до 180 градусов.

Географическая долгота – длина дуги экватора в градусах от начального меридиана (0 градусов) до меридиана заданной точки.

Начальным меридианом считается Гринвичский меридиан (0 градусов).

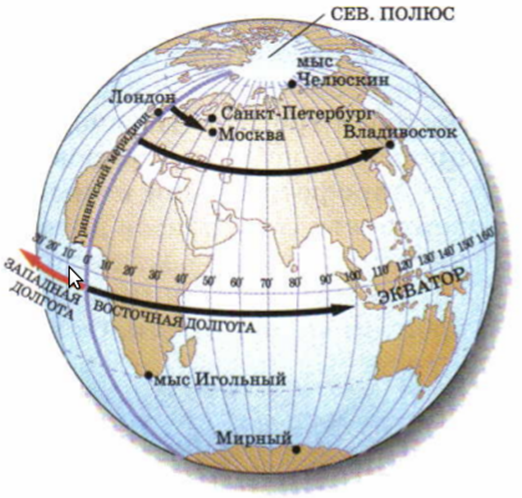
Рис. 2. Определение долгот (Источник)

Чтобы определить долготу, нужно найти меридиан, на котором находится заданный объект.

Например, долгота Москвы – 37 градусов и 37 минут восточной долготы, записывается это так: 37°37′ в.д.; долгота Мехико – 99°08′ з.д.

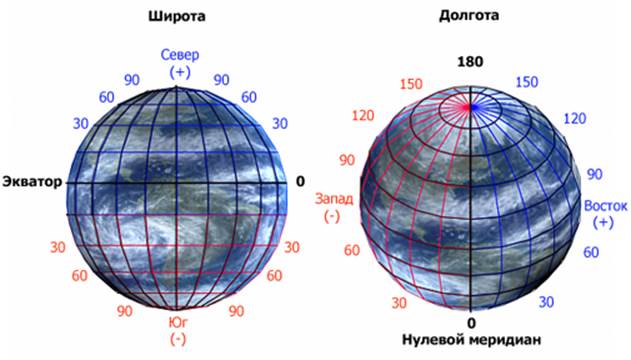
Рис. 3. Географическая широта и географическая долгота

Для точного определения местонахождения объекта на поверхности Земли надо знать его географическую широту и географическую долготу.

Географические координаты – величины, определяющие положение точки на земной поверхности с помощью широт и долгот.

Например, Москва имеет следующие географические координаты: 55°45′ с.ш. и 37°37′ в.д. Город Пекин имеет следующие координаты: 39°56′ с.ш. 116°24′ в.д. Сначала записывается значение широты.

Иногда требуется найти объект по уже заданным координатам, для этого надо сначала предположить, в каких полушариях находится данный объект.

Домашнее задание

Параграфы 12, 13.

1. Что такое географическая широта и долгота?

Список литературы

Основная

1. Начальный курс географии: Учеб. для 6 кл. общеобразоват. учреждений / Т.П. Герасимова, Н.П. Неклюкова. – 10-е изд., стереотип. – М.: Дрофа, 2010. – 176 с.

2. География. 6 кл.: атлас. – 3-е изд., стереотип. – М.: Дрофа, ДИК, 2011. – 32 с.

3. География. 6 кл.: атлас. – 4-е изд., стереотип. – М.: Дрофа, ДИК, 2013. – 32 с.

4. География. 6 кл.: конт. карты. – М.: ДИК, Дрофа, 2012. – 16 с.

Энциклопедии, словари, справочники и статистические сборники

1. География. Современная иллюстрированная энциклопедия / А.П. Горкин. – М.: Росмэн-Пресс, 2006. – 624 с.

Литература для подготовки к ГИА и ЕГЭ

1. География: начальный курс. Тесты. Учеб. пособие для учащихся 6 кл. – М.: Гуманит. изд. центр ВЛАДОС, 2011. – 144 с.

2. Тесты. География. 6-10 кл.: Учебно-методическое пособие / А.А. Летягин. – М.: ООО «Агентство «КРПА «Олимп»: «Астрель», «АСТ», 2001. – 284 с.

Материалы в сети Интернет

1. Федеральный институт педагогических измерений (Источник).

2. Русское Географическое Общество (Источник).

3. Geografia.ru (Источник).

Высота над уровнем моря — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 10 ноября 2019; проверки требуют 6 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 10 ноября 2019; проверки требуют 6 правок.

Высота́ над у́ровнем мо́ря, высота́ — линейная мера разности потенциалов в точке земной поверхности и в начале счёта высот (исходном пункте). В исходном пункте высота принимается равной нулю.

Разность потенциалов силы тяжести в полной мере характеризует положение двух точек по высоте: вода течёт из точки с меньшим потенциалом в точку с большим потенциалом.

Следует отличать следующие понятия:

высоту (разность высот) в используемой системе от простой суммы нивелирных превышений: сумма нивелирных превышений зависит от пути, по которому выполнено геометрическое нивелирование.
высоту (разность высот) в используемой системе от геодезической высоты точки. Геодезическая высота точки — расстояние от точки до поверхности отсчётного земного эллипсоида, она не связана с разностью потенциалов (т. е. вода может течь в сторону возрастания геодезической высоты). Геодезическая высота отличается от высоты над уровнем моря на аномалию высоты.

История понятия

К середине XIX в. стало ясно, что при определении высот из геометрического нивелирования нельзя более полагать выводимые превышения равными разностям расстояний от центра Земли — необходимо иметь в виду нецентральность земного гравитационного поля, непараллельность уровенных поверхностей потенциала земной силы тяжести. А. П. Болотов ^[1], следуя французскому академику Л. Пюиссану ^[2]^[3] отметил возможность счета высот по перпендикулярам к сфероидальным поверхностям, параллельным поверхности океана. Л. Пюиссан в книге 1805 г. описал принципы геометрического нивелирования, не использовав сам термин «нивелирование» (сс. 230—237), но имея в виду поправки за рефракцию по Лапласу (сс. 223—229). Разности высот считал равными разностям расстояний до центра сферической Земли. Термин «нивелирование» появился в книге Пюиссана 1807 г. ^[4] Лаплас ^[5] дал описание астрономической и земной рефракции и измерение высоты барометром.

Внимание геодезистов к этому кругу вопросов привлекла в 1870 г. невязка в ~1,2 м полигона геометрического нивелирования, пересекшего Альпы у Симплона и Сен-Готарда. Позднее выяснилось, что эта невязка — результат просчета и влияние силы тяжести в подобных случаях едва ли будет больше дециметра. Теодор Ванд ^[6], Г. Захарие (G. Zachariae), Ф. Р. Гельмерт опубликовали свои работы о счете высот в земном гравитационном поле в этот период. Вклад выдающегося немецкого геодезиста Гельмерта ^[7] (и последующие публикации) особенно значителен. Именно он правильно оценил упомянутое влияние, им предложены динамические высоты, до сих пор сохранившие свою роль в теории и практике нивелирования (термин появился позднее) и метод вычисления ортометрических высот, служивший в нашей стране до замены таких высот нормальными. Разрабатывая теорию ортометрических высот — высот над геоидом Гаусса-Листинга, Гельмерт отметил принципиальную невозможность точного их определения по результатам измерений на земной поверхности.

В 1945 г. М. С. Молоденский (ЦНИИГАиК) впервые использовал нормальные высоты для решения задачи совместного определения фигуры Земли и внешнего гравитационного поля ^[8]. Дальнейшее развитие система нормальных высот получила в работах канд. техн. наук В. Ф. Еремеева (ЦНИИГАиК), и окончательно разработана к 1972 г. ^[9]

Основные системы высот над уровнем моря

Динамическая высота (перевод разности потенциалов на линейную меру делением на постоянную величину, близкую к средней силе тяжести, например, среднее значение нормальной силы тяжести на широте 45°). Динамические высоты удобно применять вблизи одной и той же уровенной поверхности замкнутого водоёма или гидротехнического сооружения, в этом случае измеренные превышения не будут отличаться от соответствующей разности динамических высот. Применение динамических высот для решения геодезических задач неудобно, поскольку потребуется вводить поправку за переход к динамическим даже в линии нивелирования низкой точности.
Ортометрическая высота (отрезок силовой линии реального поля силы тяжести от геоида Брунса до точки земной поверхности; разность потенциалов переводится в линейную меру делением на среднее интегральное значение реальной силы тяжести вдоль этого отрезка). Приращения ортометрической высоты по вертикали в точности равны приращению длины.
Нормальная высота (отрезок силовой линии нормального поля силы тяжести от поверхности уровенного эллипсоида вверх до точки, в которой разность нормального потенциала равна разности реального потенциала; разность потенциалов переводится в линейную меру делением на величину среднего интегрального значения нормальной силы тяжести вдоль этого отрезка). Отметки нормальных высот, хотя и в общем случае непостоянны для одной и той же уровенной поверхности, лучше характеризуют уровенные поверхности с разными потенциалами, чем ортометрические. Приращения нормальной высоты по вертикали не равны приращению длины и соответствуют затуханию аномального гравитационного поля с высотой.
Нормально-ортометрическая высота (отрезок силовой линии нормального поля силы тяжести от земной поверхности вниз до точки, в которой разность нормального потенциала равна разности реального потенциала; разность потенциалов переводится в линейную меру делением на величину среднего интегрального значения нормальной силы тяжести вдоль этого отрезка).

Исходный пункт счёта высот

В России и в Казахстане высоты точек земной поверхности над уровнем моря отсчитывают от среднемноголетнего уровня Балтийского моря, зафиксированного отметкой на Кронштадтском футштоке.

Балтийская система высот

В России в качестве государственной системы высот используется Балтийская система нормальных высот 1977 года, определенная по результатам уравнивания измерений на пунктах государственной нивелирной сети I и II классов главной высотной основы, выполненного ГУГК СССР в 1977 году. Отсчёт нормальных высот в Балтийской системе нормальных высот 1977 года ведется от нуля Кронштадтского футштока. За нуль Кронштадтского футштока принята горизонтальная черта на медной пластине Тонберга, укрепленной в устое Синего моста через Обводной канал в г. Кронштадте. Отметка горизонтальной черты пластины Тонберга равна 0,000 м. Строго говоря, исходным пунктом служит вековой репер вблизи футштока, связанный с началом счёта высот.

Примеры

Высоты горных вершин над уровнем моря определены наклонным визирным лучом из тригонометрическим нивелированием с точностью около 1 м, тогда как геодезическая высота вершины над отсчётным эллипсоидом может быть определена с точностью до 1 см с помощью геодезических ГНСС-приёмников.

См. также

Примечания

↑ Болотов А. П. Геодезия или руководство к исследованию общего вида Земли, построению карт и производству тригонометрической и топографической съемок и нивелировок. Часть II: проекции карт, нивелирование, топография.. — СПб.: К. Вингебер, 1837. — 445 с.
↑ Puissant L. Traité de géodésie ou exposition des méthodes astronomiques et trigonométriques, appliquées soit à la mesure de la terre, soit à la confection du canevas des cartes et des plans. — 1. — Paris: Courcier, 1807. — С. 230.
↑ Puissant L. Traité de géodésie ou exposition des méthodes astronomiques et trigonométriques, appliquées soit à la mesure de la terre, soit à la confection du canevas des cartes et des plans. — 2. — Paris: Courcier, 1819. — С. 350.
↑ Puissant L. Traité de topographie, d’arpentage et de nivellement. — Paris: Courcier, 1807. — 332 с.
↑ Laplace Pierre-Simon. Traité de Mécanique céleste, t. 4. — 1. — Paris: L’Imprimerie Royale, 1805.
↑ Wand Th. Die Principien der mathematischen Physik und Potentialtheorie. — Leipzig: B. G. Teubner, 1871. — 184 с.
↑ F. R. Helmert. Zur Theorie des geometrischen Nivellirens (Deutsch) // Astronomische Nachrichten : журнал. — 1873. — Т. 81, № 19. — С. 298-300. — ISSN 1521-3994.
↑ Молоденский М. С. Основные вопросы геодезической гравиметрии. — Труды ЦНИИГАиК, вып. 42. — Москва: Геодезиздат, 1945. — 108 с.
↑ Еремеев В. Ф., Юркина М. И. Теория высот в гравитационном поле Земли. — Труды ЦНИИГАиК, вып. 191. — Москва: Недра, 1972. — 144 с.
↑ Mount Everest — Peakbagger.com
↑ BBC Russian — В мире — Китай согласился «приподнять» Эверест на 4 метра

Источники

Ссылки

Гравиметрия и геодезия (Бровар Б.В., Юркина М.И., Тулин В.А., Спиридонов А.И., Демьянов Г.В., Галаганов О.Н., Родкин М.В., Таранов В.А., Кафтан В.И., Жаров В.Е., Авсюк Ю.Н., Светлосанова З.П., Толчельникова С.А., Пик М.В., Молоденский С.М., Денисов В.И., Мельников В.Н., Измайлов В.П., Карагиоз О.В., Колосницын Н.И., Нейман Ю.М., Бывшев В.А., Гусев Н.А., Баграмянц В.О., Копаев А.В., Сорока А.И., Непоклонов В.Б., Кузнецов Ю.Г., Майоров А.Н., Щеглов С.Н., Медведев П.П., Лебедев С.А., Зуева А.Н., Плешаков Д.И., Дубовской В.Б., Конопихин А.А., Соловьев Ю.Ю., Чуйкова Н.А., Пасынок С.Л., Максимова Т.Г., Казарян С.А., Васин М.Г., Попков Д.И., Леонтьев В.И., Сбитнев А.В., Жильников В.Г., Латышев Д.Д., Четверикова А.А.) М.: Научный мир, 2010, 562 с. ISBN: 978-5-91522-189-4

Литература

Измерение расстояний с помощью градусной сетки — урок. География, 5 класс.

С помощью градусной сетки на географической карте и глобусе можно определять расстояния. Все меридианы — одинаковой длины, поэтому известно, что длины их дуг величиной $1°$ составляют $111,3$ км.

Длины дуг величиной $1°$ для разных параллелей неодинаковы — они уменьшаются от экватора к полюсам. Для расчётов используют таблицу значений длин дуг $1°$ параллелей для разных широт:

Широта	Длина $1°$, км
$0°$	$111,3$
$5°$	$110,9$
$10°$	$109,6$
$15°$	$107,6$
$20°$	$104,6$
$25°$	$102,1$
$30°$	$96,5$
$35°$	$91,3$
$40°$	$85,4$
$45°$	$78,8$
$50°$	$71,7$
$55°$	$64,0$
$60°$	$55,8$
$65°$	$47,2$
$70°$	$38,2$
$75°$	$28,9$
$80°$	$19,4$
$85°$	$9,7$
$90°$	$0$

Определение расстояний по параллели

Длины дуг величиной $1°$ для разных параллелей неодинаковы — они уменьшаются от экватора к полюсам.

$А =$ ($д1$$+$ $д2$) $·$ $104,6$ (длина $1°$ на широте $20°$) $=$ ($10° +$ $20°$) $·$ $104,6 =$ $30°$ $·$ $104,6 =$ $3 138$ км.

$Б =$ ($д1$ $–$ $д2$) $·$ $109,6 =$ ($20° –$ $10°$) $·$ $109,6 =$ $10° ·$ $109,6 =$ $1 096$ км.

$В =$ ($д2$ $–$ $д1$) $·$ $96,5 =$ ($90° –$ $60°$) $·$ $96,5 =$ $30° ·$ $96,5 =$ $2 895$ км.

Определение расстояний по меридиану

Длина дуги $1°$ меридиана приблизительно равна $111,3$ км ($20 000$ км $:$ $180° =$ $111,3$ км).

$А =$ ($ш1$$+$ $ш2$) $·$ $111,3 =$ ($20° +$ $10°$) $·$ $111,3 =$ $30° ·$ $111,3 =$ $3 339$ км.

$Б =$ ($ш1$ $–$ $ш2$) $·$ $111,3 =$ ($40° –$ $10°$) $·$ $111,3 =$ $30° ·$ $111,3 =$ $3 339$ км.

$В =$ ($ш2$ $–$ $ш1$) $·$ $111,3 =$ ($30° –$ $10°$) $·$ $111,3 =$ $20° ·$ $111,3 =$ $2 226$ км.

Система координат — Википедия

Систе́ма координа́т — комплекс определений, реализующий метод координат, то есть способ определять положение и перемещение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки.

В математике координаты — совокупность чисел, сопоставленных точкам многообразия в некоторой карте определённого атласа.

В элементарной геометрии координаты — величины, определяющие положение точки на плоскости и в пространстве. На плоскости положение точки чаще всего определяется расстояниями от двух прямых (координатных осей), пересекающихся в одной точке (начале координат) под прямым углом; одна из координат называется ординатой, а другая — абсциссой. В пространстве по системе Декарта положение точки определяется расстояниями от трёх плоскостей координат, пересекающихся в одной точке под прямыми углами друг к другу, или сферическими координатами, где начало координат находится в центре сферы.

В географии координаты выбираются как (приближённо) сферическая система координат — широта, долгота и высота над известным общим уровнем (например, океана). См. Географические координаты.

В астрономии небесные координаты — упорядоченная пара угловых величин (например, прямое восхождение и склонение), с помощью которых определяют положение светил и вспомогательных точек на небесной сфере. В астрономии употребляют различные системы небесных координат. Каждая из них по существу представляет собой сферическую систему координат (без радиальной координаты) с соответствующим образом выбранной фундаментальной плоскостью и началом отсчёта. В зависимости от выбора фундаментальной плоскости система небесных координат называется горизонтальной (плоскость горизонта), экваториальной (плоскость экватора), эклиптической (плоскость эклиптики) или галактической (галактическая плоскость).

Наиболее используемая система координат — прямоугольная система координат (также известная как декартова система координат).

Координаты на плоскости и в пространстве можно вводить бесконечным числом разных способов. Решая ту или иную математическую или физическую задачу методом координат, можно использовать различные координатные системы, выбирая ту из них, в которой задача решается проще или удобнее в данном конкретном случае. Известным обобщением системы координат являются системы отсчёта и системы референции.

Точка P и её координаты в трёхмерной системе координат (с осью Х, направленной к читателю)

В этом разделе даются разъяснения к наиболее употребляемым системам координат в элементарной математике.

Декартовы координаты[править | править код]

Расположение точки P на плоскости определяется декартовыми координатами с помощью пары чисел (x,y):{\displaystyle (x,y):}

x{\displaystyle x} — расстояние от точки P до оси y с учетом знака
y{\displaystyle y} — расстояние от точки P до оси x с учетом знака

В пространстве необходимы уже три координаты (x,y,z):{\displaystyle (x,y,z):}

x{\displaystyle x} — расстояние от точки P до плоскости yz
y{\displaystyle y} — расстояние от точки P до плоскости xz
z{\displaystyle z} — расстояние от точки P до плоскости xy

Полярные координаты[править | править код]

Полярные координаты.

В полярной системе координат, применяемой на плоскости, положение точки P определяется её расстоянием до начала координат r = |OP| и углом φ её радиус-вектора к оси Ox.

В пространстве применяются обобщения полярных координат — цилиндрические и сферические системы координат.

Цилиндрические координаты[править | править код]

Цилиндрические координаты.

Цилиндрические координаты — трёхмерный аналог полярных, в котором точка P представляется упорядоченной тройкой (r,φ,z).{\displaystyle (r,\varphi ,z).} В терминах декартовой системы координат,

0⩽r{\displaystyle 0\leqslant {r}} (радиус) — расстояние от оси z до точки P,
0⩽φ<360∘{\displaystyle 0\leqslant \varphi <360^{\circ }} (азимут или долгота) — угол между положительной («плюсовой») частью оси x и отрезком, проведённым от полюса до точки P и спроектированной на плоскость xy.
z{\displaystyle z} (высота) равна декартовой z-координате точки P.

Примечание: в литературе для первой (радиальной) координаты иногда используется обозначение ρ, для второй (угловой, или азимутальной) — обозначение θ, для третьей координаты — обозначение h.

Полярные координаты имеют один недостаток: значение φ не определено при r = 0.

Цилиндрические координаты полезны для изучения систем, симметричных относительно некоторой оси. Например, длинный цилиндр с радиусом R в декартовых координатах (с осью z, совпадающей с осью цилиндра) имеет уравнение x2+y2=R2,{\displaystyle x^{2}+y^{2}=R^{2},} тогда как в цилиндрических координатах оно выглядит гораздо проще, как r = R.

Сферические координаты[править | править код]

$x^{2}+y^{2}=R^{2},$ Сферические координаты.

Сферические координаты — трёхмерный аналог полярных.

В сферической системе координат расположение точки P определяется тремя компонентами: (ρ,φ,θ).{\displaystyle (\rho ,\varphi ,\theta ).} В терминах декартовой системы координат,

0⩽ρ{\displaystyle 0\leqslant \rho } (радиус) — расстояние от точки P до полюса,
0⩽φ⩽360∘{\displaystyle 0\leqslant \varphi \leqslant 360^{\circ }} (азимут или долгота) — угол между положительной («плюсовой») полуосью x и проекцией отрезка, проведённого из полюса до точки P, на плоскость xy.
0⩽θ⩽180∘{\displaystyle 0\leqslant \theta \leqslant 180^{\circ }} (широта или полярный угол) — угол между положительной («плюсовой») полуосью z и отрезком, проведённым из полюса до точки P.

Примечание: в литературе иногда азимут обозначается θ, а полярный угол — φ. Иногда для радиальной координаты используется r вместо ρ. Кроме того, диапазон углов для азимута может выбираться как (−180°, +180°] вместо диапазона [0°, +360°). Наконец, полярный угол может отсчитываться не от положительного направления оси z, а от плоскости xy; в этом случае он лежит в диапазоне [−90°, +90°], а не в диапазоне [0°, 180°]. Иногда порядок координат в тройке выбирается отличным от описанного; например, полярный и азимутальный углы могут быть переставлены.

Сферическая система координат также имеет недостаток: φ и θ не определены, если ρ = 0; угол φ не определён также и для граничных значений θ = 0 и θ = 180° (или для θ = ±90°, в случае принятия соответствующего диапазона для этого угла).

Для построения точки P по её сферическим координатам нужно от полюса вдоль положительной полуоси z отложить отрезок, равный ρ, повернуть его на угол θ вокруг оси y в направлении положительной полуоси x, и затем повернуть на угол θ вокруг оси z в направлении положительной полуоси y.

Сферические координаты полезны при изучении систем, симметричных относительно точки. Так, уравнение сферы с радиусом R в декартовых координатах с началом отсчёта в центре сферы выглядит как x2+y2+z2=R2,{\displaystyle x^{2}+y^{2}+z^{2}=R^{2},} тогда как в сферических координатах оно становится намного проще: ρ=R.{\displaystyle \rho =R.}

Другие распространённые системы координат[править | править код]

Аффинная (косоугольная) система координат — прямолинейная система координат в аффинном пространстве. На плоскости задается точкой начала координат О и двумя упорядоченными неколлинеарными векторами, которые представляют собой аффинный базис. Осями координат в данном случае называются прямые, проходящие через точку начала координат параллельно векторам базиса, которые, в свою очередь, задают положительное направление осей. В трехмерном пространстве, соответственно, аффинная система координат задается тройкой линейно независимых векторов и точкой начала координат. Для определения координат некоторой точки М вычисляются коэффициенты разложения вектора ОМ по векторам базиса^[1].
Барицентрические координаты были впервые введены в 1827 году А. Мебиусом, решавшим вопрос о центре тяжести масс, расположенных на вершинах треугольника. Они аффинно инвариантны, представляют собой частный случай общих однородных координат. Точка с барицентрическими координатами расположена в n-мерном векторном пространстве Eⁿ, а собственно координаты при этом относятся к фиксированной системе точек, которые не лежат в (n−1)-мерном подпространстве. Барицентрические координаты используются также и в алгебраической топологии применительно к точкам симплекса^[2].
Биангулярные координаты — частный случай бицентрических координат, система координат на плоскости, задаваемая двумя фиксированными точками С₁ и С₂, через которые проводится прямая, выступающая в качестве оси абсцисс. Позиция некоторой точки P, которая не лежит на этой прямой, определяется углами PC₁C₂ и PC₂C₁.
Биполярные координаты ^[3] характеризуются тем, что в качестве координатных линий на плоскости в этом случае выступают два семейства окружностей с полюсами A и B, а также семейство окружностей, ортогональных к ним. Преобразование биполярных координат в декартовы прямоугольные осуществляется посредством специальных формул. Биполярные координаты в пространстве называются бисферическими; в этом случае координатными поверхностями являются сферы, поверхности, образуемые вращением дуг окружностей, а также полуплоскости, проходящие через ось O_z^[4].
Бицентрические координаты — всякая система координат, которая основана на двух фиксированных точках и в рамках которой положение некоторой другой точки определяется, как правило, степенью её удаления или вообще позицией относительно этих двух основных точек. Системы подобного рода могут быть довольно полезны в определённых сферах научных исследований^[5]^[6].
Бицилиндрические координаты — система координат, которая образуется в том случае, если система биполярных координат на плоскости O_xy параллельно переносится вдоль оси O_z. В качестве координатных поверхностей в этом случае выступают семейство пар круговых цилиндров, оси которых параллельны, семейство ортогональных к ним круговых цилиндров, а также плоскость. Для перевода бицилиндрических координат в декартовы прямоугольные для трехмерного пространства также применяются специальные формулы^[7].
Конические координаты — трехмерная ортогональная система координат, состоящая из концентрических сфер, которые описываются посредством их радиуса, и двух семейств перпендикулярных конусов, расположенных вдоль осей x и z^[8].
Координаты Риндлера используются преимущественно в рамках теории относительности и описывают ту часть плоского пространства-времени, которая обыкновенно называется пространством Минковского. В специальной теории относительности равномерно ускоряющаяся частица находится в гиперболическом движении, и для каждой такой частицы в координатах Риндлера может быть выбрана такая точка отсчёта, относительно которой она покоится.
Параболические координаты — это двумерная ортогональная система координат, в которой координатными линиями является совокупность конфокальных парабол. Трехмерная модификация параболических координат строится путём вращения двумерной системы вокруг оси симметрии этих парабол. У параболических координат также имеется определенный спектр потенциальных практических приложений: в частности, они могут использоваться применительно к эффекту Штарка. Параболические координаты связаны определенным отношением с прямоугольными декартовыми^[9].
Проективные координаты существуют, согласно наименованию, в проективном пространстве П_n (К) и представляют собой взаимно однозначное соответствие между его элементами и классами конечных подмножеств элементов тела К, характеризующихся свойствами эквивалентности и упорядоченности. Для определения проективных координат проективных подпространств достаточно определить соответствующие координаты точек проективного пространства. В общем случае относительно некоторого базиса проективные координаты вводятся чисто проективными средствами^[10].
Тороидальная система координат — трехмерная ортогональная система координат, получаемая в результате вращения двумерной биполярной системы координат вокруг оси, разделяющей два её фокуса. Фокусы биполярной системы, соответственно, превращаются в кольцо с радиусом а, лежащее на плоскости xy тороидальной системы координат, в то время как ось z становится осью вращения системы. Фокальное кольцо также называют иногда базовой окружностью^[11].
Трилинейные координаты являются одним из образцов однородных координат и имеют своей основой заданный треугольник, так что положение некоторой точки определяется относительно сторон этого треугольника — главным образом степенью удаленности от них, хотя возможны и другие вариации. Трилинейные координаты могут быть относительно просто преобразованы в барицентрические; кроме того, они также конвертируемы в двумерные прямоугольные координаты, для чего используются соответствующие формулы^[12].
Цилиндрические параболические координаты — трехмерная ортогональная система координат, получаемая в результате пространственного преобразования двумерной параболической системы координат. Координатными поверхностями, соответственно, служат конфокальные параболические цилиндры. Цилиндрические параболические координаты связаны определенным отношением с прямоугольными, могут быть применены в ряде сфер научных исследований^[13].
Эллипсоидальные координаты — эллиптические координаты в пространстве. Координатными поверхностями в данном случае являются эллипсоиды, однополостные гиперболоиды, а также двуполостные гиперболоиды, центры которых расположены в начале координат. Система ортогональна. Каждой тройке чисел, являющихся эллипсоидальными координатами, соответствуют восемь точек, которые относительно плоскостей системы O_xyz симметричны друг другу^[14].

Переход из одной системы координат в другую[править | править код]

Декартовы и полярные[править | править код]

x=rcos⁡φ,{\displaystyle x=r\,\cos \varphi ,}

y=rsin⁡φ,{\displaystyle y=r\,\sin \varphi ,}

r=x2+y2,{\displaystyle r={\sqrt {x^{2}+y^{2}}},}

φ=arctg⁡yx+πu0(−x)sgn⁡y,{\displaystyle \varphi =\operatorname {arctg} {\frac {y}{x}}+\pi u_{0}(-x)\,\operatorname {sgn} y,}

где u₀ — функция Хевисайда с u0(0)=0,{\displaystyle u_{0}(0)=0,} а sgn — функция signum. Здесь функции u₀ и sgn используются как «логические» переключатели, аналогичные по значению операторам «если .. то» (if…else) в языках программирования. Некоторые языки программирования имеют специальную функцию atan2 (y, x), которая возвращает правильный φ в необходимом квадранте, определённом координатами x и y.

Декартовы и цилиндрические[править | править код]

x=rcos⁡φ,{\displaystyle x=r\,\cos \varphi ,}

y=rsin⁡φ,{\displaystyle y=r\,\sin \varphi ,}

z=z.{\displaystyle z=z.\quad }

r=x2+y2,{\displaystyle r={\sqrt {x^{2}+y^{2}}},}

φ=arctg⁡yx+πu0(−x)sgn⁡y,{\displaystyle \varphi =\operatorname {arctg} {\frac {y}{x}}+\pi u_{0}(-x)\,\operatorname {sgn} y,}

z=z.{\displaystyle z=z.\quad }

(dxdydz)=(rcos⁡θ−rsin⁡φ0rsin⁡θrcos⁡φ0001)⋅(drdφdz),{\displaystyle {\begin{pmatrix}dx\\dy\\dz\end{pmatrix}}={\begin{pmatrix}r\cos \theta &-r\sin \varphi &0\\r\sin \theta &r\cos \varphi &0\\0&0&1\end{pmatrix}}\cdot {\begin{pmatrix}dr\\d\varphi \\dz\end{pmatrix}},}

(drdφdz)=(xx2+y2yx2+y20−yx2+y2xx2+y20001)⋅(dxdydz).{\displaystyle {\begin{pmatrix}dr\\d\varphi \\dz\end{pmatrix}}={\begin{pmatrix}{\frac {x}{\sqrt {x^{2}+y^{2}}}}&{\frac {y}{\sqrt {x^{2}+y^{2}}}}&0\\{\frac {-y}{\sqrt {x^{2}+y^{2}}}}&{\frac {x}{\sqrt {x^{2}+y^{2}}}}&0\\0&0&1\end{pmatrix}}\cdot {\begin{pmatrix}dx\\dy\\dz\end{pmatrix}}.}

Декартовы и сферические[править | править код]

x=ρsin⁡θcos⁡φ,{\displaystyle {x}=\rho \,\sin \theta \,\cos \varphi ,\quad }

y=ρsin⁡θsin⁡φ,{\displaystyle {y}=\rho \,\sin \theta \,\sin \varphi ,\quad }

z=ρcos⁡θ;{\displaystyle {z}=\rho \,\cos \theta ;\quad }

ρ=x2+y2+z2,{\displaystyle {\rho }={\sqrt {x^{2}+y^{2}+z^{2}}},}

θ=arccos⁡zρ=arctg⁡x2+y2z,{\displaystyle {\theta }=\arccos {\frac {z}{\rho }}=\operatorname {arctg} {\frac {\sqrt {x^{2}+y^{2}}}{z}},}

φ=arctg⁡yx+πu0(−x)sgn⁡y.{\displaystyle {\varphi }=\operatorname {arctg} {\frac {y}{x}}+\pi \,u_{0}(-x)\,\operatorname {sgn} y.}

(dxdydz)=(sin⁡θcos⁡φρcos⁡θcos⁡φ−ρsin⁡θsin⁡φsin⁡θsin⁡φρcos⁡θsin⁡φρsin⁡θcos⁡φcos⁡θ−ρsin⁡θ0)⋅(dρdθdφ),{\displaystyle {\begin{pmatrix}dx\\dy\\dz\end{pmatrix}}={\begin{pmatrix}\sin \theta \cos \varphi &\rho \cos \theta \cos \varphi &-\rho \sin \theta \sin \varphi \\\sin \theta \sin \varphi &\rho \cos \theta \sin \varphi &\rho \sin \theta \cos \varphi \\\cos \theta &-\rho \sin \theta &0\end{pmatrix}}\cdot {\begin{pmatrix}d\rho \\d\theta \\d\varphi \end{pmatrix}},}

(dρdθdφ)=(x/ρy/ρz/ρxzρ2×2+y2yzρ2×2+y2−(x2+y2)ρ2×2+y2−yx2+y2xx2+y20)⋅(dxdydz).{\displaystyle {\begin{pmatrix}d\rho \\d\theta \\d\varphi \end{pmatrix}}={\begin{pmatrix}x/\rho &y/\rho &z/\rho \\{\frac {xz}{\rho ^{2}{\sqrt {x^{2}+y^{2}}}}}&{\frac {yz}{\rho ^{2}{\sqrt {x^{2}+y^{2}}}}}&{\frac {-(x^{2}+y^{2})}{\rho ^{2}{\sqrt {x^{2}+y^{2}}}}}\\{\frac {-y}{x^{2}+y^{2}}}&{\frac {x}{x^{2}+y^{2}}}&0\end{pmatrix}}\cdot {\begin{pmatrix}dx\\dy\\dz\end{pmatrix}}.}

Цилиндрические и сферические[править | править код]

r=ρsin⁡θ,{\displaystyle {r}=\rho \,\sin \theta ,}

φ=φ,{\displaystyle {\varphi }=\varphi ,\quad }

z=ρcos⁡θ;{\displaystyle {z}=\rho \,\cos \theta ;}

ρ=r2+z2,{\displaystyle {\rho }={\sqrt {r^{2}+z^{2}}},}

θ=arctg⁡zr+πu0(−r)sgn⁡z,{\displaystyle {\theta }=\operatorname {arctg} {\frac {z}{r}}+\pi \,u_{0}(-r)\,\operatorname {sgn} z,}

φ=φ.{\displaystyle {\varphi }=\varphi .\quad }

(drdφdh)=(sin⁡θρcos⁡θ0001cos⁡θ−ρsin⁡θ0)⋅(dρdθdφ),{\displaystyle {\begin{pmatrix}dr\\d\varphi \\dh\end{pmatrix}}={\begin{pmatrix}\sin \theta &\rho \cos \theta &0\\0&0&1\\\cos \theta &-\rho \sin \theta &0\end{pmatrix}}\cdot {\begin{pmatrix}d\rho \\d\theta \\d\varphi \end{pmatrix}},}

(dρdθdφ)=(rr2+z20zr2+z2−zr2+z20rr2+

высокие широты — это… Что такое высокие широты?

высокие широты: high latitudes

высокие частоты
высокий

Смотреть что такое «высокие широты» в других словарях:

высокие широты — Условное название приполярных областей земного шара, ограниченных примерно 65° северной и южной широты … Словарь по географии
Высокие широты — (high latitudes)High latitudes, термин, которым часто называют околополюсные широты к С. и Ю. от 60о … Страны мира. Словарь
Климат — (от греч. klíma, родительный падеж klímatos, буквально наклон; подразумевается наклон земной поверхности к солнечным лучам) многолетний режим погоды, свойственный той или иной местности на Земле и являющийся одной из ее географических… … Большая советская энциклопедия
Земля (планета) — Земля (от общеславянского зем пол, низ), третья по порядку от Солнца планета Солнечной системы, астрономический знак Å или, ♀. I. Введение З. занимает пятое место по размеру и массе среди больших планет, но из планет т. н. земной группы, в… … Большая советская энциклопедия
Земля — I Земля (от общеславянского зем пол, низ) третья по порядку от Солнца планета Солнечной системы, астрономический знак ⊕ или, ♀. I. Введение З. занимает пятое место по размеру и массе среди больших планет, но из планет т … Большая советская энциклопедия
Климат — (греч. κλίμα, κλίματος означает наклон солнца, иначе сказать, полуденную высоту солнца). Древние географы делили Землю на климатические пояса в зависимости от этого явления и длины дня, принимая в расчет так называемые астрономические климаты,… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
климат — а; м. [от греч. klima (klimatos) наклон (солнечных лучей)] 1. Многолетний режим погоды, свойственный той или иной местности на Земле и являющийся одной из её географических характеристик. Изменение климата. Жаркий, умеренный, континентальный,… … Энциклопедический словарь
Арктика — сев. полярная обл. Земли. Название от греч. арктикос северный, полярный из греч. арктос медведь сев. полярная обл. находится непосредственно под созвездием Большой Медведицы. Географические названия мира: Топонимический словарь. М: АСТ. Поспелов… … Географическая энциклопедия
Узкозубая акула — Научная класс … Википедия
КООРДИНАТНАЯ СЕТКА — в топографии сеть воображаемых линий, опоясывающих земной шар в широтном и меридиональном направлениях, с помощью которой можно точно определить положение любой точки на земной поверхности. Отсчет широт ведется от экватора большой окружности,… … Энциклопедия Кольера
координатная сетка — в топографии сеть воображаемых линий, опоясывающих земной шар в широтном и меридиональном направлениях, с помощью которой можно точно определить положение любой точки на земной поверхности. Отсчет широт ведется от экватора – большой окружности,… … Географическая энциклопедия

Книги

Высокие широты. 100 фотографий, Хворостов Сергей Николаевич. «Высокие широты. 100 фотографий»-книга посвящена Арктике и Антарктике, экстремальным экспедициям, обитателям полярных широт и всем тем, кто связал свою жизнь с полюсами. Есть на Земле такие… Подробнее Купить за 1771 руб
Высокие широты. 100 фотографий, Хворостов С.. «Высокие широты. 100 фотографий»-книга посвящена Арктике и Антарктике, экстремальным экспедициям, обитателям полярных широт и всем тем, кто связал свою жизнь с полюсами. Есть на Земле такие… Подробнее Купить за 1450 руб
Высокие широты, Образцов П.А.. Книга повествует об открытии и освоении Арктики и Антарктики, этих двух полюсов холода и мужества, об отважных героях, благодаря которым человечество узнало о природе, животном мире самых… Подробнее Купить за 591 руб

Другие книги по запросу «высокие широты» >>

Широта	Длина \(1°\), км
\(0°\)	\(111,3\)
\(5°\)	\(110,9\)
\(10°\)	\(109,6\)
\(15°\)	\(107,6\)
\(20°\)	\(104,6\)
\(25°\)	\(102,1\)
\(30°\)	\(96,5\)
\(35°\)	\(91,3\)
\(40°\)	\(85,4\)
\(45°\)	\(78,8\)
\(50°\)	\(71,7\)
\(55°\)	\(64,0\)
\(60°\)	\(55,8\)
\(65°\)	\(47,2\)
\(70°\)	\(38,2\)
\(75°\)	\(28,9\)
\(80°\)	\(19,4\)
\(85°\)	\(9,7\)
\(90°\)	\(0\)