Какой буквой в физике обазначается длина?
Другие предметы …..й@ ЛёЛьК@………)))))))) 2 (239) Какой буквой в физике обазначается длина? 8 летОтветы
ВОЛЬНЫЙ СТРЕЛОК 4 (656)Избранные
КАТЕГОРИИ
Авто, Мото Автострахование Выбор автомобиля, мотоцикла Оформление авто-мото сделок ГИБДД, Обучение, Права Сервис, Обслуживание, Тюнинг ПДД, Вождение Прочие Авто-темы Автоспорт Бизнес, Финансы Макроэкономика Производственные предприятия Собственный бизнес Страхование Банки и Кредиты Недвижимость, Ипотека Бухгалтерия, Аудит, Налоги Остальные сферы бизнеса Долги, Коллекторы Знакомства, Любовь, Отношения Любовь Знакомства Отношения Расставания Дружба Прочие взаимоотношения Компьютеры, Связь Интернет Железо Программное обеспечение Прочее компьютерное Мобильные устройства Офисная техника Мобильная связь Образование Детские сады Школы ВУЗы, Колледжи Дополнительное образование Образование за рубежом Прочее образование Философия, Непознанное Мистика, Эзотерика Психология Религия, Вера Прочее непознанное Философия Путешествия, Туризм Самостоятельный отдых Документы Отдых в России Отдых за рубежом Прочее туристическое Семья, Дом, Дети Строительство и Ремонт Беременность, Роды Воспитание детей Мебель, Интерьер Домашняя бухгалтерия Домоводство Загородная жизнь Свадьба, Венчание, Брак Организация быта Прочие дела домашние Спорт Футбол Хоккей Экстрим Другие виды спорта Занятия спортом События, результаты Спортсмены Зимние виды спорта Стиль, Мода, Звезды Мода Светская жизнь и Шоубизнес Прочие тенденции стиля жизни Стиль, Имидж Темы для взрослых Другое О проектах Mail.ru Ответы Mail.ru Почта Mail.ru Прочие проекты Новости Mail.ru Агент Mail.ru Мой Мир Mail.ru ICQ Облако Mail.ru Красота и Здоровье Коррекция веса Здоровый образ жизни Врачи, Клиники, Страхование Болезни, Лекарства Косметика, Парфюмерия Баня, Массаж, Фитнес Уход за волосами Маникюр, Педикюр Детское здоровье Салоны красоты и СПА Прочее о здоровье и красоте Животные, Растения Домашние животные Комнатные растения Сад-Огород Дикая природа Прочая живность Города и Страны Вокруг света Карты, Транспорт, GPS Климат, Погода, Часовые пояса Коды, Индексы, Адреса ПМЖ, Недвижимость Прочее о городах и странах Общество, Политика, СМИ Общество Политика Прочие социальные темы Средства массовой информации Еда, Кулинария Закуски и Салаты Первые блюда Вторые блюда Напитки Десерты, Сладости, Выпечка Консервирование Торжество, Праздник Готовим детям Готовим в … Покупка и выбор продуктов На скорую руку Прочее кулинарное Фотография, Видеосъемка Обработка и печать фото Обработка видеозаписей Выбор, покупка аппаратуры Уход за аппаратурой Техника, темы, жанры съемки Прочее фото-видео Товары и Услуги Идеи для подарков Техника для дома Прочие промтовары Сервис, уход и ремонт Прочие услуги Досуг, Развлечения Хобби Концерты, Выставки, Спектакли Охота и Рыбалка Клубы, Дискотеки Рестораны, Кафе, Бары Советы, Идеи Игры без компьютера Прочие развлечения Новый Год День Святого Валентина Восьмое марта Наука, Техника, Языки Гуманитарные науки Естественные науки Лингвистика Техника Работа, Карьера Написание резюме Подработка, временная работа Кадровые агентства Отдел кадров, HR Профессиональный рост Смена и поиск места работы Обстановка на работе Трудоустройство за рубежом Прочие карьерные вопросы Гороскопы, Магия, Гадания Гороскопы Гадания Сны Прочие предсказания Магия Юридическая консультация Административное право Гражданское право Конституционное право Семейное право Трудовое право Уголовное право Финансовое право Жилищное право Право социального обеспечения Военная служба Паспортный режим, регистрация Прочие юридические вопросы Юмор Золотой фонд Искусство и Культура Музыка Литература Кино, Театр Живопись, Графика Архитектура, Скульптура Прочие искусства Компьютерные и Видео игры Прочие Браузерные Клиентские Консольные Мобильные Программирование Другие языки и технологии Java JavaScript jQuery MySQL Perl PHP Python Веб-дизайн Верстка, CSS, HTML, SVG Системное администрирование Домашние задания Другие предметы Литература Математика Алгебра Геометрия Иностранные языки Химия Физика Биология История География Информатика Экономика Русский язык Обществознание Плесский колледж бизнеса и туризма AmwayVlasovi GS Logistica SpezServis manul_toy© Mail.Ru, 2018
Чертёжный шрифт — Википедия
| Чертёжный шрифт | |
|---|---|
 | |
| Стиль | рублёный, пропорциональный, минималистичный |
| Классификация | технический |
| Использование | в чертежах |
| Набор символов | русский, латинский, греческий алфавиты, технические символы |
 Медиафайлы на Викискладе Медиафайлы на Викискладе | |
Чертёжный шрифт — рукописный и компьютерный шрифт, который применяется для оформления чертежей и других технических документов. Шрифт стандартизован, его описывает международный стандарт ISO 3098 и такие национальные стандарты, как ГОСТ 2.304-81 и DIN 6776-1. Надписи чертёжным шрифтом могут выполняются от руки с использованием прямоугольной или наклонной сетки, могут использоваться трафареты и сухой перенос, а также компьютерный набор.[1]
Согласно требованиям системы стандартов ЕСКД все надписи на чертежах должны быть выполнены чертёжным шрифтом по ГОСТ 2.304-81[источник не указан 374 дня], а в текстовых документах чертёжный шрифт должен использоваться при рукописном способе выполнения[2].
Стандарт устанавливает высоту и ширину символов, толщину линии, расстояния между символами строками и словами.
Главным требованием к шрифту было, чтобы текст был прост в написании и удобен в прочтении.[источник не указан 374 дня] ISO 3098 и ГОСТ 2.304-81 определяет написание для латинского, кириллического и греческого алфавитов, арабских и римских цифр.
Международный стандарт ISO 3098 состоит из шести частей под общим наименованием «Документация техническая на продукцию. Шрифт для надписей и обозначений»:[3][4]
- ISO 3098-1:2015 Общие требования
- ISO 3098-2:2000 Латинский алфавит, цифры и знаки
- ISO 3098-3:2000 Греческий алфавит
- ISO 3098-4:2000 Диакритические и специальные знаки для латинского алфавита
- ISO 3098-5:1997 Шрифт из букв латинского алфавита, цифр и знаков для систем автоматизированного проектирования
- ISO 3098-6:2000 Кириллица
Входящий в Единую систему конструкторской документации (ЕСКД) межгосударственный стандарт ГОСТ 2.304-81 Шрифты чертёжные введён в 1982 году, полностью соответствует стандартам Совета экономической взаимопомощи СТ СЭВ 851-78-СТ СЭВ 855-78 и заменяет предшествовавший стандарт ГОСТ 2.304-68.
Стандарт Немецкого института стандартизации DIN 6776-1 «Чертежи технические. Надписи, шрифтовые знаки» соответствует стандарту ISO 3098.
 Размеры шрифта: высота прописных (h) и строчных (c) букв, ширина буквы g, толщина линии d
Размеры шрифта: высота прописных (h) и строчных (c) букв, ширина буквы g, толщина линии dВысота шрифта[править | править код]
Размером шрифта называется высота прописных (заглавных) букв в миллиметрах. Размер (высота) шрифта обозначается буквой h.
Стандарт устанавливает следующие размеры шрифта: 1,8; 2,5; 3,5; 5; 7; 10; 14; 20; 28; 40. Размер 1,8 не рекомендуется, но допускается. Размеры 1,8 и 2,5 не допускаются, если чертёж выполняется карандашом. Для стандартного чертежа предпочтительными являются размеры 3,5; 5 и 7. Высота строчных букв равна предыдущему размеру шрифта. Так, если размер шрифта — 10, то высота прописных букв — 10 мм, а высота строчных —7.
Выносные элементы[править | править код]
Термин «высота шрифта» не учитывает выносных элементов символов, которые выполняются за счёт промежутков между строками. Выносные элементы имеют прописные буквы Д, Й, Ц, Щ и строчные буквы
Толщина линии шрифта[править | править код]
Толщина линии шрифта обозначается буквой d.
Существуют два типа шрифтов — тип А, у которого толщина линии в 14 раз меньше его размера (d = 1/14 h) и тип Б (в ISO 3098 обозначается латинской «B»), у которого толщина линии в 10 раз меньше его размера (d = 1/10 h). Поскольку ширина шрифта прямо пропорциональна толщине линии, шрифт А более узок, чем Б.
Ширина шрифта[править | править код]
Чертёжный шрифт является пропорциональным, то есть разные буквы могут иметь разную ширину.
Ширина шрифта обозначается буквой g и является прямо пропорциональной величине d. Самая широкая буква шрифта — Щ (g = 9d). Самые узкие буквы шрифта — з, с (g = 4d).
Ширина всех русских букв приведена в таблице.
| Ширина | Буква |
|---|---|
| 9d | Щ |
| 8d | Ж, Ф, Ш, Ъ, Ы |
| 7d | Д, М, Х, Ю, ж, т, ф, ш, щ, ы, ю |
| 6d | Б, В, Е, И, К, Л, Н, О, П, Р, Т, У, Ч, Э, Я, а, м, ц, ъ |
| 5d | Г, З,С, б, в, г, д, е, и, й, к, л, н, о, п, р, у, х, ч, ь, э, я |
| 4d | з, с |
Расстояния[править | править код]
Расстояния между буквами и цифрами делают вдвое больше толщины линии, то есть равными 2d. Расстояния между словами и числами делают такими, чтобы в них могла поместиться буква O, то есть равными 6d. Расстояния между нижними границами строк делают равными 17d.
| Параметры шрифта | Обозначение | Относительный размер | Размеры, мм | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Размер шрифта — высота прописных букв | h | (14/14)h | 2,5 | 3,5 | 5 | 7 | 10 | 14 | 20 |
| Высота строчных букв | c | (10/14)h | 1,8[T 1] | 2,5 | 3,5 | 5 | 7 | 10 | 14 |
| Расстояние между буквами | a | (2/14)h | 0,35 | 0,5 | 0,7 | 1 | 1,4 | 2 | 2,8 |
| Минимальный шаг строк (высота вспомогательной сетки) | b | (20/14)h | 3,5 | 5 | 7 | 10 | 14 | 20 | 28 |
| Минимальное расстояние между словами | e | (6/14)h | 1,05 | 1,5 | 2,1 | 3 | 4,2 | 6 | 8,4 |
| Толщина линий шрифта | d | (1/14)h | 0,18 | 0,25 | 0,35 | 0,5 | 0,7 | 1 | 1,4 |
| Параметры шрифта | Обозначение | Относительный размер | Размеры, мм | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Размер шрифта — высота прописных букв | h | (10/10)h | 1,8[T 1] | 2,5 | 3,5 | 5 | 7 | 10 | 14 | 20 |
| Высота строчных букв | c | (7/10)h | 1,3[T 1] | 1,8[T 1] | 2,5 | 3,5 | 5 | 7 | 10 | 14 |
| Расстояние между буквами | a | (2/10)h | 0,35 | 0,5 | 0,7 | 1 | 1,4 | 2 | 2,8 | 4 |
| Минимальный шаг строк (высота вспомогательной сетки) | b | (14/10)h | 3,1 | 3,5 | 5 | 7 | 10 | 14 | 20 | 28 |
| Минимальное расстояние между словами | e | (6/10)h | 1,1 | 1,5 | 2,1 | 3 | 4,2 | 6 | 8,4 | 12 |
| Толщина линий шрифта | d | (1/10)h | 0,18 | 0,25 | 0,35 | 0,5 | 0,7 | 1 | 1,4 | 2 |
- ↑ 1 2 3 4 Размер шрифта 1,8 мм отсутствует в ISO 3098 и «не рекомендуется» стандартом ГОСТ 2.304-81
В чертежах допускается, как прямой, так и наклонный (наклон составляет примерно 75°) шрифт. Наклон можно начертать с помощью двух угольников. Принцип начертания шрифта при этом не изменяется, меняют направление только вертикальные линии сетки.
Набор трафаретов для нанесения шрифтов DIN 6776В тех случаях, когда требуется сделать надпись чертёжным шрифтом вручную, проводят верхнюю и нижнюю линию строки. Для выполнения средних элементов букв Б, В, Е, Н, Р, У, Ч, Ъ, Ы, Я проводят горизонтальную линию посредине строки. Для букв З, О, Ф, Ю проводят ещё две горизонтальные линии, указывающие границы скруглений.
Существуют специальные трафареты для быстрого выполнения надписей.
- ГОСТ 2.304-81 «Единая система конструкторской документации. Шрифты чертежные».
- А. Д. Ботвиников, В. Н. Виноградов, И. С. Вышнепольский. Техника выполнения чертежей и правила их оформления. Правила оформления чертежей. 2.4. Шрифты чертёжные // Черчение 9 класс. — Москва: ACT, Астрель, 2008. — С. 22—25. — 223 с. — ISBN 978-5-17-045068-8.
- osifont — свободный шрифт, соответствующий ISO 3098
Ø — Википедия
Материал из Википедии — свободной энциклопедии
| Буква латиницы O с диагональным штрихом | |
|---|---|
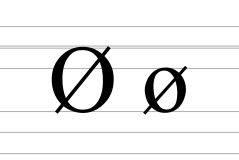
| Øø | |
Изображение
| |
| Ø: latin capital letter o with stroke ø: latin small letter o with stroke | |
| Юникод | Ø: U+00D8 ø: U+00F8 |
| HTML-код | Ø: ø: |
| UTF-16 | Ø: 0xD8 ø: 0xF8 |
| Ø: %C3%98 ø: %C3%B8 | |
| Мнемоника | Ø: Øø: ø |
Ø, ø (O с диагональным штрихом) — буква расширенной латиницы, используемая в датском, норвежском и фарерском алфавитах для передачи огублённого гласного переднего ряда средне-верхнего подъёма. Также ранее использовалась в Юнифоне для английского языка[1].
Для более точной фонетической передачи французского eu, немецкого ö, скандинавского ø (которые не подразумевают смягчения согласных) в начале XX века предлагался вариант транслитерации на русский язык при помощи буквы Ӭ.
| Символ (TeX) (Команда (TeX)) | Символ (Юникод) | Название | Значение | Пример |
|---|---|---|---|---|
| Произношение | ||||
| Раздел математики | ||||
| ⇒{\displaystyle \Rightarrow } (\Rightarrow) →{\displaystyle \rightarrow } (\rightarrow) ⊃{\displaystyle \supset } (\supset) | ⇒ → ⊃ | Импликация, следование | A⇒B{\displaystyle A\Rightarrow B} означает «если A{\displaystyle A} верно, то B{\displaystyle B} также верно». (→ может использоваться вместо ⇒ или для обозначения функции, см. ниже.) (⊃ может использоваться вместо ⇒ или для обозначения надмножества, см. ниже.). | x=2⇒x2=4{\displaystyle x=2\Rightarrow x^{2}=4} верно, но x2=4⇒x=2{\displaystyle x^{2}=4\Rightarrow x=2} неверно (так как x=−2{\displaystyle x=-2} также является решением). |
| «влечёт» или «если…, то» или «отсюда следует» | ||||
| везде | ||||
| ⇔{\displaystyle \Leftrightarrow } (\Leftrightarrow) | ⇔ | Равносильность | A⇔B{\displaystyle A\Leftrightarrow B} означает «A{\displaystyle A} верно тогда и только тогда, когда B{\displaystyle B} верно». | x+5=y+2⇔x+3=y{\displaystyle x+5=y+2\Leftrightarrow x+3=y} |
| «если и только если» или «равносильно» | ||||
| везде | ||||
| ∧{\displaystyle \wedge } (\wedge) | ∧ | Конъюнкция | A∧B{\displaystyle A\wedge B} истинно тогда и только тогда, когда A{\displaystyle A} и B{\displaystyle B} оба истинны. | (n>2)∧(n<4)⇔(n=3){\displaystyle (n>2)\wedge (n<4)\Leftrightarrow (n=3)}, если n{\displaystyle n} — натуральное число. |
| «и» | ||||
| Математическая логика | ||||
| ∨{\displaystyle \vee } (\vee) | ∨ | Дизъюнкция | A∨B{\displaystyle A\vee B} истинно, когда хотя бы одно из условий A{\displaystyle A} и B{\displaystyle B} истинно. | (n⩽2)∨(n⩾4)⇔n≠3{\displaystyle (n\leqslant 2)\vee (n\geqslant 4)\Leftrightarrow n\neq 3}, если n{\displaystyle n} — натуральное число. |
| «или» | ||||
| Математическая логика | ||||
| ¬{\displaystyle \neg } (\neg) | ¬ | Отрицание | ¬A{\displaystyle \neg A} истинно тогда и только тогда, когда ложно A{\displaystyle A}. | ¬(A∧B)⇔(¬A)∨(¬B){\displaystyle \neg (A\wedge B)\Leftrightarrow (\neg A)\vee (\neg B)} x∉S⇔¬(x∈S){\displaystyle x\notin S\Leftrightarrow \neg (x\in S)} |
| «не» | ||||
| Математическая логика | ||||
| ∀{\displaystyle \forall } (\forall) | ∀ | Квантор всеобщности | ∀x,P(x){\displaystyle \forall x,P\left(x\right)} обозначает «P(x){\displaystyle P\left(x\right)} верно для всех x{\displaystyle x}». | ∀n∈N,n2⩾n{\displaystyle \forall n\in \mathbb {N} ,\;n^{2}\geqslant n} |
| «Для любых», «Для всех», «Для всякого» | ||||
| Математическая логика | ||||
| ∃{\displaystyle \exists } (\exists) | ∃ | Квантор существования | ∃x,P(x){\displaystyle \exists x,\;P\left(x\right)} означает «существует хотя бы один x{\displaystyle x} такой, что верно P(x){\displaystyle P\left(x\right)}» | ∃n∈N,n+5=2n{\displaystyle \exists n\in \mathbb {N} ,\;n+5=2n} (подходит число 5) |
| «существует» | ||||
| Математическая логика | ||||
| ={\displaystyle =} | = | Равенство | x=y{\displaystyle x=y} обозначает «x{\displaystyle x} и y{\displaystyle y} обозначают одно и то же значение». | 1 + 2 = 6 − 3 |
| «равно» | ||||
| везде | ||||
| :={\displaystyle :=} :⇔{\displaystyle :\Leftrightarrow } | := :⇔
| Определение | x:=y{\displaystyle x:=y} означает «x{\displaystyle x} по определению равен y{\displaystyle y}». P:⇔Q{\displaystyle P:\Leftrightarrow Q} означает «P{\displaystyle P} по определению равносильно Q{\displaystyle Q}» | ch(x):=12(ex+e−x){\displaystyle {\rm {ch}}\left(x\right):={1 \over 2}\left(e^{x}+e^{-x}\right)} (определение гиперболического косинуса) A⊕B:⇔(A∨B)∧¬(A∧B){\displaystyle A\oplus B:\Leftrightarrow (A\vee B)\wedge \neg (A\wedge B)} (определение исключающего «ИЛИ») |
| «равно/равносильно по определению» | ||||
| везде | ||||
| {,}{\displaystyle \{,\}} | { } | Множество элементов | {a,b,c}{\displaystyle \{a,\;b,\;c\}} означает множество, элементами которого являются a{\displaystyle a}, b{\displaystyle b} и c{\displaystyle c}. | N={1,2,…}{\displaystyle \mathbb {N} =\{1,\;2,\;\ldots \}} (множество натуральных чисел) |
| «Множество…» | ||||
| Теория множеств | ||||
| {|}{\displaystyle \{|\}} | {|} | Множество элементов, удовлетворяющих условию | {x|P(x)}{\displaystyle \{x\,|\,P\left(x\right)\}} означает множество всех x{\displaystyle x} таких, что верно P(x){\displaystyle P\left(x\right)}. | {n∈N|n2<20}={1,2,3,4}{\displaystyle \{n\in \mathbb {N} \,|\,n^{2}<20\}=\{1,\;2,\;3,\;4\}} |
| «Множество всех… таких, что верно…» | ||||
| Теория множеств | ||||
| ∅{\displaystyle \varnothing } (\varnothing) {}{\displaystyle \{\}} | ∅ {} | Пустое множество | {}{\displaystyle \{\}} и ∅{\displaystyle \varnothing } означают множество, не содержащее ни одного элемента. | {n∈N|1<n2<4}=∅{\displaystyle \{n\in \mathbb {N} \,|\,1<n^{2}<4\}=\varnothing } |
| «Пустое множество» | ||||
| Теория множеств | ||||
| ∈{\displaystyle \in } (\in) ∉{\displaystyle \notin } (\notin) | ∈ ∉ | Принадлежность/непринадлежность к множеству | a∈S{\displaystyle a\in S} означает «a{\displaystyle a} является элементом множества S{\displaystyle S}» a∉S{\displaystyle a\notin S} означает «a{\displaystyle a} не является элементом множества S{\displaystyle S}» | 2∈N{\displaystyle 2\in \mathbb {N} } 12∉N{\displaystyle {1 \over 2}\notin \mathbb {N} } |
| «принадлежит», «из» «не принадлежит» | ||||
| Теория множеств | ||||
| ⊆{\displaystyle \subseteq } (\subseteq) ⊂{\displaystyle \subset } (\subset) | ⊆ ⊂ | Подмножество | A⊆B{\displaystyle A\subseteq B} означает «каждый элемент из A{\displaystyle A} также является элементом из B{\displaystyle B}». A⊂B{\displaystyle A\subset B} обычно означает то же, что и A⊆B{\displaystyle A\subseteq B}. Однако некоторые авторы используют ⊂{\displaystyle \subset }, чтобы показать строгое включение (то есть ⊊{\displaystyle \subsetneq }). | (A∩B)⊆A{\displaystyle (A\cap B)\subseteq A} Q⊆R{\displaystyle \mathbb {Q} \subseteq \mathbb {R} } |
| «является подмножеством», «включено в» | ||||
| Теория множеств | ||||
| ⊇{\displaystyle \supseteq } (\supseteq) ⊃{\displaystyle \supset } (\supset) | ⊇ ⊃ | Надмножество | A⊇B{\displaystyle A\supseteq B} означает «каждый элемент из B{\displaystyle B} также является элементом из A{\displaystyle A}». A⊃B{\displaystyle A\supset B} обычно означает то же, что и A⊇B{\displaystyle A\supseteq B}. Однако некоторые авторы используют ⊃{\displaystyle \supset }, чтобы показать строгое включение (то есть ⊋{\displaystyle \supsetneq }). | (A∪B)⊇A{\displaystyle (A\cup B)\supseteq A} R⊇Q{\displaystyle \mathbb {R} \supseteq \mathbb {Q} } |
| «является надмножеством», «включает в себя» | ||||
| Теория множеств | ||||
| ⊊{\displaystyle \subsetneq } (\subsetneq) | ⊊ | Собственное подмножество | A⊊B{\displaystyle A\subsetneq B} означает A⊆B{\displaystyle A\subseteq B} и A≠B{\displaystyle A\neq B}. | N⊊Q{\displaystyle \mathbb {N} \subsetneq \mathbb {Q} } |
| «является собственным подмножеством», «строго включается в» | ||||
| Теория множеств | ||||
| ⊋{\displaystyle \supsetneq } (\supsetneq) | ⊋ | Собственное надмножество | A⊋B{\displaystyle A\supsetneq B} означает A⊇B{\displaystyle A\supseteq B} и A≠B{\displaystyle A\neq B}. | Q⊋N{\displaystyle \mathbb {Q} \supsetneq \mathbb {N} } |
| «является собственным надмножеством», «строго включает в себя» | ||||
| Теория множеств | ||||
| ∪{\displaystyle \cup } (\cup) | ∪ | Объединение | A∪B{\displaystyle A\cup B} означает множество, содержащее все элементы из A{\displaystyle A} и B{\displaystyle B} | A⊆B⇔A∪B=B{\displaystyle A\subseteq B\Leftrightarrow A\cup B=B} |
| «Объединение … и …», «…, объединённое с …» | ||||
| Теория множеств | ||||
| ∩{\displaystyle \cap } (\cap) | ⋂ | Пересечение | A∩B{\displaystyle A\cap B} означает множество одинаковых элементов, принадлежащих и A{\displaystyle A}, и B{\displaystyle B}. | {x∈R|x2=1}∩N={1}{\displaystyle \{x\in \mathbb {R} \,|\,x^{2}=1\}\cap \mathbb {N} =\{1\}} |
| «Пересечение … и … «, «…, пересечённое с …» | ||||
| Теория множеств | ||||
| ∖{\displaystyle \setminus } (\setminus) | \ | Разность множеств | A∖B{\displaystyle A\setminus B} означает множество элементов, принадлежащих A{\displaystyle A}, но не принадлежащих B{\displaystyle B}. | {1,2,3,4}∖{3,4,5,6}={1,2}{\displaystyle \{1,\;2,\;3,\;4\}\setminus \{3,\;4,\;5,\;6\}=\{1,\;2\}} |
| «разность … и …», «минус», «… без …» | ||||
| Теория множеств | ||||
| →{\displaystyle \to } (\to) | → | Функция (отображение) | f:X→Y{\displaystyle f\colon X\to Y} означает функцию f{\displaystyle f} с областью определения X{\displaystyle X} и областью значений Y{\displaystyle Y}. | Функция f:Z→N∪{0}{\displaystyle f\colon \mathbb {Z} \to \mathbb {N} \cup \{0\}}, определённая как f(x)=x2{\displaystyle f\left(x\right)=x^{2}} |
| «из … в …», | ||||
| везде | ||||
| ↦{\displaystyle \mapsto } (\mapsto) | ↦ | Отображение | f:x↦f(x){\displaystyle f\colon x\mapsto f\left(x\right)} означает, что образом x{\displaystyle x} после применения функции f{\displaystyle f} будет f(x){\displaystyle f\left(x\right)}. | Функцию, определённую как |