Диаметр — это… Что такое Диаметр?
Диаметр в изначальном значении это отрезок, соединяющий две точки на окружности и проходящий через центр окружности, а также длина этого отрезка. Диаметр равен двум радиусам.
Диаметр геометрических фигур
Диаметр окружности, круга, сферы, шара
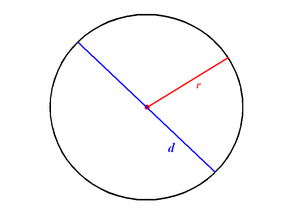Радиус (r) и диаметр (d) окружностиДиаметр — это хорда (отрезок, соединяющий две точки) на окружности (сфере, поверхности шара), и проходящий через центр этой окружности (сферы, шара). Также диаметром называют длину этого отрезка. Диаметр окружности является хордой, проходящей через её центр; такая хорда имеет максимальную длину. По величине диаметр равен двум радиусам.
Символ диаметра
Символ диаметра «⌀» (может не отображаться в некоторых браузерах) схож начертанием со строчной перечёркнутой буквой «o». В Юникоде он находится под десятичным номером 8960 или шестнадцатеричным номером 2300 (может быть введён в HTML-код как ⌀ или %%c (буква c — латинская) или \U+2205 в текстовой строке.
Во многих случаях символ диаметра может не отображаться, так как он редко включается в шрифты — например, он присутствует в Arial Unicode MS (поставляется с Microsoft Office, при установке именуется «Универсальный шрифт»), DejaVu (свободный), Code2000 (условно-бесплатный) и некоторых других.
Следует отличать символ диаметра «⌀» от других похожих на него символов:
Вариации и обобщения
Понятие диаметра допускает естественные обобщения на некоторые другие геометрические объекты.
- Под диаметром конического сечения понимается прямая проходящая через середины двух параллельных хорд.
- Под диаметром метрического пространства понимается точная верхняя грань расстояний между парами его точек. В частности:
- Диаметр графа — это максимальное из расстояний между парами его вершин. Расстояние между вершинами определяется как наименьшее число рёбер, которые необходимо пройти, чтобы добраться из одной вершины в другую. Иначе говоря, это расстояние между двумя вершинами графа, максимально удаленными друг от друга.
- Диаметр геометрической фигуры — максимальное расстояние между точками этой фигуры.
- Диаметром множества , лежащего в метрическом пространстве с метрикой , называется величина . Например, диаметр n-размерного гиперкуба со стороной s равен
- .
См. также
Литература
Способы вставки символа (значок) диаметра «Ø» (в том числе и в Word), их особенности
На компьютерной клавиатуре присутствуют не все символы. Нет на ней и символа диаметра. Общепринятое обозначение диаметра выглядит следующим образом — «Ø». Но при этом существует масса способов вставить его во многих различных приложениях. Наиболее популярным среди них является использование кодов ASCII. Второй способ связан с офисным пакетом компании Microsoft и работает только там. Третий метод это применение буфера обмена. Для его исполнения нужен непосредственно сам значок диаметра, который при помощи функции «копирования» и «вставки» будет вставлен в нужное приложение.
Все способы будут подробно рассмотрены и представлены в этой статье.
В каких ситуациях появляется потребность символа диаметра?
Перечислять примеры применения значка диаметра можно бесконечно долго, но и так понятно, что в некоторых ситуациях без него приходится достаточно трудно либо не комфортно. Именно поэтому далее по тексту мы рассмотрим три способа вставки символа диаметра в электронный документ.
Первый способ
Самым популярным способом можно назвать использование кодов ASCII. Он может быть осуществлен непосредственно самой ОС Windows. Для его реализации важно знать код – «0216», который в таблице кодов ASCII распознается как знак «Ø». Алгоритм ввода будет таковым:
- Выбираем язык ввода «английский».
- Следим за тем, чтобы клавиша «Num Lock» была включена, если сверху кнопки она не горит, то нужно ее включить.
- После чего заходим в наше приложение. Следующим действием наводим наш указатель «мыши» (стрелочку) на рабочую зону и кликаем один раз левой кнопкой. Курсор должен замигать.
- Теперь нажимаем клавишу «Alt» (неважно с какой стороны, слева или справа). После чего, не отжимая ее, на клавиатуре справа нажимаем
Главное достоинство данного способа это то, что он универсален. Он может работать во многих существующих приложениях. Особенность способа состоит в том что сам символ, в качестве исходника не нужен. Недостаток данного метода в том, что всегда нужно знать код.
Второй способ
Программа Word и другие приложения взаимозаменяемый метод ввода «Ø» связан с определенным набором таких программных приложений, как: Microsoft Office Word, Excel и других.
Теперь можно наблюдать открывшееся окно вставки. Находим нужный нам знак «Ø» за счет прокрутки найденных символов. В этом нам поможет колесо мыши. После удачного поиска «Ø», выделяем его одним нажатием левой кнопки мыши и кликаем кнопку «Вставить». После этого закрываем окно. Затем наверняка появиться значок диаметра в Word (в рабочей зоне). Отрицательная сторона данного способа в том, что он будет работать только в одной группе программных продуктов. Поэтому везде его применить невозможно.
Третий способ
Так же одним из способов вставки «Ø» является применение буфера обмена и использование функций «Копировать» и «Вставить». Буфер обмена это определенная часть памяти компьютерной операционной системы, которая предназначена для временного хранения информации. Сначала требуется найти где-нибудь такой символ.
В качестве примера, можно значок диаметра вставить в ворд (word) в соответствии с вышеизложенным алгоритмом. После чего его выделяем и копируем (по желанию можно использовать так называемые горячие клавиши «Ctrl»+»C»). Затем заходим в иное приложение и осуществляем действие вставки («Ctrl»+»V»). Отрицательная сторона данного способа заключается в том, что в любом случае нужен исходный символ. А так бывает далеко не всегда.
Каждый пользователь может выбрать для себя наиболее подходящий способ вставки символа (знака) диаметра — «Ø», учитывая свой индивидуальный подход и персональные навыки.
Видео
В видео — наглядный пример, как вставить в Word значок диаметра.
Окружность, радиус, диаметр, число Пи, сектор, касательная
Окружность — геометрическое место точек плоскости, расстояние от которых до центра окружности равно.
Центр окръжности
Радиус: расстояние от центра окружности до его границы.
Диаметр: наибольшее расстояние от одной границы окружности до другой. Диаметр равен двум радиусам.
$d = 2\cdot r$
Периметр (длина окружности): длина границы окружности.
Длина окружности $= \pi \cdot$ диаметр $= 2 \cdot \pi \cdot$ радиус
Длина окружности $= \pi \cdot d = 2 \cdot \pi \cdot r$
$\pi$ — pi: число, равное 3,141592… или $\approx \frac{22}{7}$, то есть отношение $\frac{\text{длины окружности}}{\text{диаметр}}$ любого окружности.
Дуга: изогнутая линия, которая является частью окружности.
Дуги окружности измеряется в градусах или радианах.
Например: 90° или $\frac{\pi}{2}$ — четверть круга,
180° или $\pi$ — половина круга.
Сумма всех дуг окружности составляет 360° или $2\pi$
Хорда: отрезок прямой, соединяющей две точки на окружности.
Сектор: похож на часть пирога (клин).
Касательная к окружности: прямая, перпендикулярна к радиусу, и имеющая ТОЛЬКО одну общую точку с окуржностью.
Формулы
Длина окружности $=\pi \cdot \text{диаметр} = 2\cdot \pi \cdot \text{радиус}$
Площадь круга $= \pi \cdot$ радиус2
Радиус обозначается как r, диаметр как d, длина окружности как P и площадь как S.
$P = \pi \cdot d = 2\cdot \pi \cdot r$
$S = \pi \cdot r^2$
Площадь сектора круга
Площадь сектора круга K: (с центральным углом $\theta$ и радиусом $r$).
Если угол $\theta$ в градусах, тогда площадь = $\frac{\theta}{360} \pi r^2$
Если угол $\theta$ в радианах, тогда площадь, тогда площадь = $\frac{\theta}{2} r^2$
Углы
Центральный угол
Если длина дуги составляет $\theta$ градуов или радиан, то значение центрального угла также $\theta$ (градусов или радиан).
Если вы знаете длину дуги (в дюймах, ярдах, футах, сантиметрах, метрах …) вы можете найти значение её соответствующего центрального угла ($\theta$) по формуле:
$\theta = 360 \cdot \frac{l}{P} = \frac{360 \cdot l}{2 \cdot \pi \cdot r} = \frac{180 \cdot l}{\pi \cdot r}$
$l$ — длина дуги.
Вписанный угол
Вписанный угол это угол с вершиной на окружности и со сторонами, которые содержат хорды окружности.
На рисунке, угол APB это вписанный угол.
Пример:
$\widehat{AB} = 84^\circ$
$\angle APB = \frac{84}{2} = 42^\circ$
Углы между двумя хордами
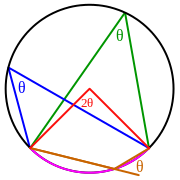
Случай 1: два секущие пересекаются внутри окружности.
Когда две секущие пересекаются внутри окружности, величина образованных угла, в два раза меньше суммы величин дуг, на которые они опираются. На рисунке дуга AB и дуга CD равны 60° и 50° тогда углы 1 и 2 равны $\frac{1}{2}(60^\circ + 50^\circ)=55^\circ$
Случай 2: две секущие пересекаются вне окружности.
Иногда секущие пересекаются за пределами окружности. Когда это случается, величина образующихся углов равна половине разности дуг, на которые они опираются.
$\angle ABC =\frac{1}{2}(x — y)$
На рисунке дуга AB=80° и дуги CD=30°.
$\angle ABC = \frac{1}{2}(80 — 30) = \frac{1}{2} \cdot 50 = 25^\circ$
Хорды
Если две хорды пересекаются внутри окружности, как на рисунке выше, тогда:
$AX \cdot XB = CX \cdot XD$
Окружность — Википедия
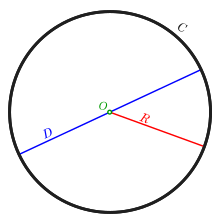Окружность (C), её центр (O), радиус (R) и диаметр (D)Окру́жность — замкнутая плоская кривая, которая состоит из всех точек на плоскости, равноудалённых от заданной точки[1]: эта точка называется центром окружности. Отрезок, соединяющий центр с какой-либо точкой окружности, называется радиусом; радиусом называется также и длина этого отрезка. Окружность разбивает плоскость на две части[2] — конечную внутреннюю и бесконечную внешнюю. Внутренность окружности называется кругом; граничные точки (то есть саму окружность) в зависимости от подхода, круг может включать или не включать.
Построение окружности циркулемПрактическое построение окружности возможно с помощью циркуля.
Окружность нулевого радиуса (вырожденная окружность) является точкой, далее этот случай исключается из рассмотрения, если не оговорено иное.
Окружность называется единичной, если её радиус равен единице. Единичная окружность является одним из основных объектов тригонометрии.
Далее всюду буква R{\displaystyle R} обозначает радиус окружности.
Прямая может иметь с окружностью не более двух общих точек.
Прямая, пересекающая окружность в двух различных точках, называется секущей. Отрезок секущей, расположенный внутри окружности, называется хордой. Хорда, проходящая через центр окружности, называется диаметром; тот же термин используется для его длины. Диаметр вдвое больше радиуса: D=2R,{\displaystyle D=2R,} он делит окружность на две равные части и поэтому является её осью симметрии. Диаметр больше любой другой хорды[3].
Хорда разбивает круг на две части, называемые сегментами круга. Два различных радиуса тоже разбивают круг на две части, называемые секторами круга (см. рисунки)[3].
Любые две несовпадающие точки окружности делят её на две части. Каждая из этих частей называется дугой окружности. Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром.
Для заданной окружности имеют место следующие свойства[3].
- Хорды, равноотстоящие от центра, равны. Обратно, если две хорды равны по длине, то они одинаково удалены от центра.
- Равным хордам соответствуют равные дуги, и наоборот.
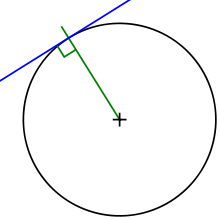
Прямая, имеющая с окружностью ровно одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности. Касательная к окружности всегда перпендикулярна её радиусу (и диаметру), проведенному в точке касания. То есть радиус является одновременно и нормалью к окружности[4].
Отрезки касательных к окружности, проведённых из одной точки, не лежащей на окружности, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности[5].
-
Вписанный угол θ равен половине величины центрального угла 2θ, опирающегося на ту же самую дугу (розового цвета)
-
К расчёту длины дуги и хорды
Центральный угол — угол с вершиной в центре окружности. Центральный угол может быть принят как угловая мера дуги, на которую он опирается. Центральный угол, образуемый дугой окружности, равной по длине радиусу, в математике принимается в качестве единицы измерения углов, и называется радиан.
Из определения радиана следует, что длина L{\displaystyle L} любой дуги окружности связана с центральным углом θ{\displaystyle \theta }, опирающимся на эту дугу, простым соотношением[6]: L=Rθ.{\displaystyle L=R\theta .} (при этом длина хорды, стягивающей ту же дугу, равна 2Rsinθ2<L{\displaystyle 2R\sin {\theta \over 2}<L}). Поскольку длина окружности равна 2πR{\displaystyle 2\pi R}, с ростом угла значение его радианной меры меняется от 0 до 2π.{\displaystyle 2\pi .}
Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают эту окружность.
Внешний угол для вписанного угла — угол, образованный одной стороной и продолжением другой стороны вписанного угла (угол θ коричневого цвета на рис.). Внешний угол для вписанного угла равен вписанному углу, опирающемуся на ту же хорду с другой стороны.
Угол между окружностью и прямой — угол между секущей прямой и одной из двух касательных к окружности в точке пересечения прямой и окружности.
Свойства вписанных углов:
- Вписанный угол либо равен половине центрального угла, опирающегося на его дугу, либо дополняет половину этого угла до 180°. Вписанный угол, опирающийся на дугу длиной в половину окружности, всегда прямой (равен 90°).
- Вписанный угол не меняет своей величины при перемещении его вершины вдоль окружности.
- Два вписанных угла, опирающиеся на одну и ту же дугу, равны.
Другие свойства:
- Угол между двумя секущими, проведёнными из точки, лежащей вне окружности, равен полуразности мер дуг, лежащих между секущими.
- Угол между пересекающимися хордами равен полусумме мер дуги, лежащей в угле, и дуги напротив неё.
- Угол между касательной и хордой, имеющими общую точку, равен половине угловой меры дуги, стягиваемой хордой.
- Изопериметрическое неравенство: Из всех замкнутых кривых данной длины окружность ограничивает область максимальной площади.
- Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.
- Говорят, что две окружности касаются, если они имеют единственную общую точку. Точка касания двух окружностей лежит на прямой, проходящей через их центры.
- Теорема о секущих: Если через произвольную точку E{\displaystyle E} проведена секущая, то произведение расстояний от этой точки до точек пересечения секущей с окружностью не зависит от выбора секущей (и равно абсолютной величине степени точки относительно окружности). Если точка E{\displaystyle E} лежит вне окружности, то из нее к окружности можно провести касательную. Квадрат длины отрезка касательной до точки касания будет равен той же величине.
- Как частный случай предыдущего, при пересечении двух хорд в произвольной точке E{\displaystyle E} получаются отрезки, произведение длин которых у одной хорды равно соответствующему произведению у другой (см. рисунок), т. е. AE⋅EB=CE⋅ED{\displaystyle AE\cdot EB=CE\cdot ED}.
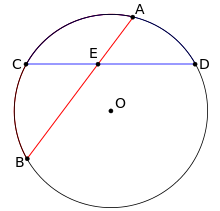AE⋅EB=CE⋅ED{\displaystyle AE\cdot EB=CE\cdot ED} 
Если радиус круга равен 1, то его окружность равна 2π.Длина окружности:
- C=2πR=πD.{\displaystyle C=2\pi R=\pi D.}
Радиус окружности:
- R=C2π=D2.{\displaystyle R={\frac {C}{2\pi }}={\frac {D}{2}}.}
Диаметр окружности:
- D=Cπ=2R.{\displaystyle D={\frac {C}{\pi }}=2R.}
Площадь круга радиуса R:
- S=πR2=πD24.{\displaystyle S=\pi R^{2}={\frac {\pi D^{2}}{4}}.}
Площадь сектора, ограниченного центральным углом α, измеряемым в градусах, радиусом R:
- S=πR2α360∘.{\displaystyle S=\pi R^{2}{\frac {\alpha }{360^{\circ }}}.}
Площадь сегмента, ограниченного дугой окружности, центральным углом α, хордой:
- S=πR2α360∘−R2sinα2.{\displaystyle S=\pi R^{2}{\frac {\alpha }{360^{\circ }}}-{\frac {R^{2}\sin \alpha }{2}}.}
Окружность, наряду с прямой, является самой распространённой кривой практически во всех областях человеческой деятельности. История её исследования и применения уходит в глубокую древность; особенную важность придало этой теме изобретение колеса. Античные учёные рассматривали прямые и окружности как единственный пример «совершенных» кривых, поэтому в геометрии считались допустимыми только построения с помощью циркуля и линейки, а движение планет моделировалось как наложение вращений по окружностям. Теории окружностей посвящена III книга «Начал» Евклида.
Также в древности было открыто, что отношение длины окружности к её диаметру (число π) одно и то же для всех окружностей. Исторически важной темой многовековых исследований было уточнение этого отношения, а также попытки решить проблему «квадратуры круга». В дальнейшем развитие теории окружностей привело к созданию тригонометрии, теории колебаний и многих других практически важных разделов науки и техники.
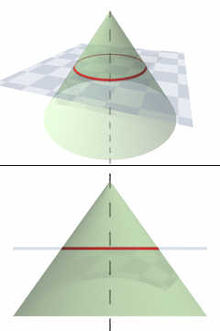Окружность получается как сечение конуса плоскостью, перпендикулярной его осиАналитическая геометрия окружностей[править | править код]
С точки зрения аналитической геометрии, окружность является простой плоской алгебраической кривой второго порядка. Окружность является частным случаем эллипса, у которого полуоси равны, и поэтому окружность относится к коническим сечениям.
Декартовы координаты[править | править код]
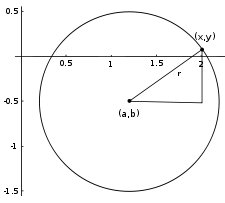Окружность радиуса r = 1, центр (a, b) = (1.2, −0.5)Общее уравнение окружности записывается как:
- x2+y2+Ax+By+C=0,{\displaystyle x^{2}+y^{2}+Ax+By+C=0,}
или
- (x−x0)2+(y−y0)2=R2,{\displaystyle \left(x-x_{0}\right)^{2}+\left(y-y_{0}\right)^{2}=R^{2},}
где
- 2×0=−A,2y0=−B,2R=A2+B2−4C.{\displaystyle 2x_{0}=-A,\;2y_{0}=-B,\;2R={\sqrt {A^{2}+B^{2}-4C}}.}
Точка (x0,y0){\displaystyle \left(x_{0},y_{0}\right)} — центр окружности, R{\displaystyle R} — её радиус.
Уравнение окружности радиуса R{\displaystyle R} с центром в начале координат:
- x2+y2=R2.{\displaystyle x^{2}+y^{2}=R^{2}.}
Уравнение окружности, проходящей через точки (x1,y1),(x2,y2),(x3,y3),{\displaystyle \left(x_{1},y_{1}\right),\left(x_{2},y_{2}\right),\left(x_{3},y_{3}\right),} не лежащие на одной прямой (с помощью определителя):
- |x2+y2xy1x12+y12x1y11x22+y22x2y21x32+y32x3y31|=0.{\displaystyle {\begin{vmatrix}x^{2}+y^{2}&x&y&1\\x_{1}^{2}+y_{1}^{2}&x_{1}&y_{1}&1\\x_{2}^{2}+y_{2}^{2}&x_{2}&y_{2}&1\\x_{3}^{2}+y_{3}^{2}&x_{3}&y_{3}&1\end{vmatrix}}=0.}
Тогда в явном виде координаты центра окружности определяются по формулам:
- x0=−12y1(x22+y22−x32−y32)+y2(x32+y32−x12−y12)+y3(x12+y12−x22−y22)x1(y2−y3)+x2(y3−y1)+x3(y1−y2){\displaystyle x_{0}=-{\frac {1}{2}}{\frac {y_{1}(x_{2}^{2}+y_{2}^{2}-x_{3}^{2}-y_{3}^{2})+y_{2}(x_{3}^{2}+y_{3}^{2}-x_{1}^{2}-y_{1}^{2})+y_{3}(x_{1}^{2}+y_{1}^{2}-x_{2}^{2}-y_{2}^{2})}{x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2})}}}
- y0=12×1(x22+y22−x32−y32)+x2(x32+y32−x12−y12)+x3(x12+y12−x22−y22)x1(y2−y3)+x2(y3−y1)+x3(y1−y2){\displaystyle y_{0}={\frac {1}{2}}{\frac {x_{1}(x_{2}^{2}+y_{2}^{2}-x_{3}^{2}-y_{3}^{2})+x_{2}(x_{3}^{2}+y_{3}^{2}-x_{1}^{2}-y_{1}^{2})+x_{3}(x_{1}^{2}+y_{1}^{2}-x_{2}^{2}-y_{2}^{2})}{x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2})}}}
Окружность также можно описать с помощью параметрического уравнения:
- {x=x0+Rcosφy=y0+Rsinφ,0⩽φ<2π.{\displaystyle {\begin{cases}x=x_{0}+R\cos \varphi \\y=y_{0}+R\sin \varphi \end{cases}},\;\;\;0\leqslant \varphi <2\pi .}
В декартовой системе координат окружность не является графиком функции, но она может быть описана как объединение графиков двух следующих функций:
- y=y0±R2−(x−x0)2.{\displaystyle y=y_{0}\pm {\sqrt {R^{2}-(x-x_{0})^{2}}}.}
Если центр окружности совпадает с началом координат, функции принимают вид:
- y=±R2−x2.{\displaystyle y=\pm {\sqrt {R^{2}-x^{2}}}.}
Полярные координаты[править | править код]
Окружность радиуса R{\displaystyle R} с центром в точке (ρ0,ϕ0){\displaystyle \left(\rho _{0},\phi _{0}\right)}:
- ρ2−2ρρ0cos(ϕ−ϕ0)+ρ02=R2.{\displaystyle \rho ^{2}-2\rho \,\rho _{0}\cos \left(\phi -\phi _{0}\right)+\rho _{0}^{2}=R^{2}.}
Если полярные координаты центра окружности ρ0=R,ϕ0=α,{\displaystyle \rho _{0}=R,\;\phi _{0}=\alpha ,} то проходящая через начало координат окружность описывается уравнением:
- ρ(φ)=2Rcos(φ−α),α−π2⩽φ⩽α+π2.{\displaystyle \rho (\varphi )=2R\cos \,(\varphi -\alpha ),\;\;\;\alpha -{\frac {\pi }{2}}\leqslant \varphi \leqslant \alpha +{\frac {\pi }{2}}.}
Если же центр является началом координат, то уравнение будет иметь вид
- ρ=R.{\displaystyle \rho =R.}
Комплексная плоскость[править | править код]
На комплексной плоскости окружность задаётся формулой:
- |z−z0|=R{\displaystyle \left|z-z_{0}\right|=R}
или в параметрическом виде
- z=z0+Reit,t∈R.{\displaystyle z=z_{0}+Re^{it},\,t\in \mathbb {R} .}
Окружности в пространстве[править | править код]
В пространстве окружность радиуса R{\displaystyle R} с центром в точке M0(x0,y0,z0){\displaystyle M_{0}(x_{0},y_{0},z_{0})} можно определить как контур диаметрального сечения сферы
- (x−x0)2+(y−y0)2+(z−z0)2=R2{\displaystyle (x-x_{0})^{2}+(y-y_{0})^{2}+(z-z_{0})^{2}=R^{2}}
плоскостью
- a⋅(x−x0)+b⋅(y−y0)+c⋅(z−z0)=0{\displaystyle a\cdot (x-x_{0})+b\cdot (y-y_{0})+c\cdot (z-z_{0})=0},
где a,b,c{\displaystyle a,b,c} — параметры, не равные одновременно нулю; то есть все точки, лежащие на данной окружности, есть решения системы
- {(x−x0)2+(y−y0)2+(z−z0)2=R2,a⋅(x−x0)+b⋅(y−y0)+c⋅(z−z0)=0.{\displaystyle {\begin{cases}(x-x_{0})^{2}+(y-y_{0})^{2}+(z-z_{0})^{2}=R^{2},\\a{\cdot }(x-x_{0})+b{\cdot }(y-y_{0})+c{\cdot }(z-z_{0})=0.\end{cases}}}
Например, при a=c≠0{\displaystyle a=c\neq 0} решения этой системы можно задать параметрически следующим образом:
- {x=x0+Ra2+c2⋅(c⋅cost−a⋅b⋅sinta2+b2+c2),y=y0+R⋅a2+c2a2+b2+c2⋅sint,z=z0−Ra2+c2⋅(a⋅cost+b⋅c⋅sinta2+b2+c2),t∈[0;2π).{\displaystyle {\begin{cases}x=x_{0}+{\dfrac {R}{\sqrt {a^{2}+c^{2}}}}\cdot \!\left(c\cdot \cos t-{\dfrac {a\cdot b\cdot \sin t}{\sqrt {a^{2}+b^{2}+c^{2}}}}\right)\!,\\[10pt]y=y_{0}+{\dfrac {R\cdot {\sqrt {a^{2}+c^{2}}}}{\sqrt {a^{2}+b^{2}+c^{2}}}}\cdot \sin t,\\[10pt]z=z_{0}-{\dfrac {R}{\sqrt {a^{2}+c^{2}}}}\cdot \!\left(a\cdot \cos t+{\dfrac {b\cdot c\cdot \sin t}{\sqrt {a^{2}+b^{2}+c^{2}}}}\right)\!,\end{cases}}t\in [0;2\pi ).}
Касательные и нормали[править | править код]
Уравнение касательной к окружности в точке (x1,y1
Угловой размер — Википедия
Материал из Википедии — свободной энциклопедии
Угловой размер (иногда также угол зрения) — это угол между прямыми линиями, соединяющими диаметрально противоположные крайние точки измеряемого (наблюдаемого) объекта и глаз наблюдателя.
Под угловым размером может также пониматься не плоский угол, под которым виден объект, а телесный угол.
Если отрезок длиной D перпендикулярен линии наблюдения (более того, она является серединным его перпендикуляром) и находится на расстоянии L от наблюдателя, то точная формула для углового размера этого отрезка: 2arctgD2L{\displaystyle 2\,\operatorname {arctg} {\frac {D}{2L}}}. Если размер тела D мал по сравнению с расстоянием от наблюдателя L, то угловой размер (в радианах) определяется отношением D/L, так как tgα≈α{\displaystyle \operatorname {tg} \alpha \approx \alpha } для малых углов. При удалении тела от наблюдателя (увеличении L), угловой размер тела уменьшается.
Понятие углового размера очень важно в геометрической оптике, и в особенности применительно к органу зрения — глазу. Глаз способен регистрировать именно угловой размер объекта. Его реальный, линейный размер определяется мозгом по оценке расстояния до объекта и из сравнения с другими, уже известными телами.
Согласно геометрии предмет, удалённый от глаза на расстояние, в 57 раз большее его поперечника, должен представляться наблюдателю под углом почти в 1°.
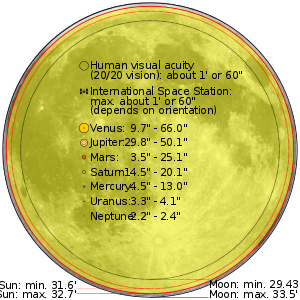Сравнение угловых размеров Солнца, Луны и планет. Размеры приведены в угловых минутах (‘) и секундах («) Иллюстрация приведена не в масштабе: для того, чтобы получить точное представление о размерах, нужно рассматривать это изображение с расстояния, в 102.6 раз превышающего ширину кружка «Moon: max.». Например, если диаметр этого кружка на вашем мониторе составляет 10 см, то смотреть следует с расстояния 10,26 м.Угловой размер астрономического объекта, видимый с Земли, обычно называется угловым диаметром или видимым диаметром. Вследствие удалённости всех объектов, угловые диаметры планет и звёзд очень малы и измеряются в угловых минутах (′) и секундах(″). Например, средний видимый диаметр Луны равен 31′05″ (вследствие эллиптичности лунной орбиты угловой размер изменяется от 29′20″ до 33′32″), или ≈0,5∘.{\displaystyle \approx 0{,}5^{\circ }.} Средний видимый диаметр Солнца — 31′59″ (изменяется от 31′31″ до 32′36″)[1]. Видимые диаметры звёзд чрезвычайно малы и лишь у немногих достигают нескольких сотых долей секунды.
Как поставить знак диаметра в Ворде — 3 способа
Знак диаметра отсутствует на клавиатуре, но, несмотря на это, его легко поставить в Ворде несколькими способами. Рассмотрим 3 варианта печати обычного и заглавного символа в порядке удобства.
ø146
Способ с автозаменой
Нажимаем клавишу «Ctrl» и, не отпуская, вводим знак «/» и английскую букву «o».
- Ctrl + «/o» = ø
- Ctrl + «/O» = Ø
Если нужен большой символ, то «o» нажимаем одновременно с клавишей «Shift».
ASCII-код знака диаметра
На английской раскладке клавиатруы зажимаем левый «Alt» и вводим цифрами справа ASCII-код символа. В зависимости от кода появляется большой или маленький диаметр.
- Alt + «0248» = ø
- Alt + «0216» = Ø
Под цифрами справа имеется ввиду этот блок клавиш:
Юникод символа
В любом месте Word документа вводим юникод диаметра и нажимаем «Alt» + «X».
- «00F8» => Alt + X = ø
- «00D8» => Alt + X = Ø
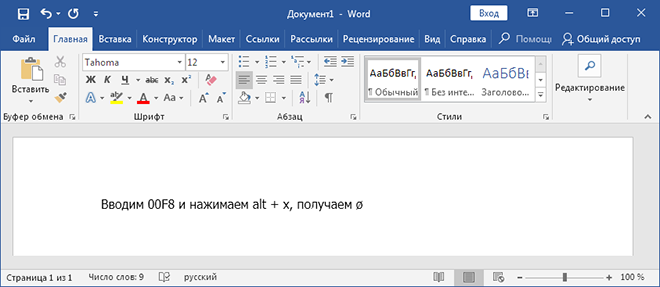
До и после юникода не должно стоять других цифр.
Ещё можно поставить диаметр без клавиатуры, выбрав его в меню «Вставка => Символы». Способ не удобный, рассматриваться не будет.
Andy Si
27 нояб. 2018 г.
34779
Что такое знак диаметра и как его найти на клавиатуре?
Начавшись во второй половине XVIII века в Англии, индустриальная революция в XIX столетии прокатилась по многим странам Европы и мира. Она характеризовалась бурным развитием техники и промышленного производства. Изготовление продукции перемещалось из мануфактур и мастерских на крупные фабрики и заводы. Однако переход от единичного и мелкосерийного производства к массовому, а также разделение труда потребовали создания разнообразной конструкторской и технологической документации, что обусловило развитие прикладной дисциплины — черчения.
Появление стандартизации
Черчение позволяет создавать графическое изображение объекта, необходимое для его изготовления. Однако для производства одного внешнего вида изделия мало. Чертеж также содержит размеры, масштаб, технические требования, материал и другие характеристики детали. Дальнейшее развитие производства привело к разделению труда, когда комплектующие изготавливаются на разных предприятиях, а потом осуществляется сборка готового изделия. Это потребовало унификации и стандартизации деталей и единого правила исполнения чертежей. Для удобства записи и восприятия технической информации были введены условные обозначения, такие как, например, знак диаметра или толщины, облегчающие запись указываемых характеристик.
Условные обозначения: знак диаметра
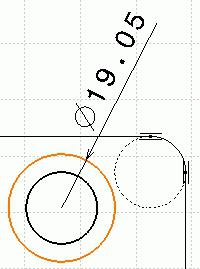
Стандартами предусмотрены различные условные обозначения, которые позволяют производить запись геометрических и технологических параметров изображенного объекта: знаки радиуса, толщины, угла, допуска и припуска обработки. К ним же относится и диаметр, которым определяются размеры отверстий и тел вращения. Хорда, соединяющая две точки на окружности (шаре) и проходящая через ее (его) центр, и называется диаметром. Как же он обозначается на чертежах? Знак диаметра представляет собой окружность, перечеркнутую линией, наклоненной под 45о к вертикали по направлению движения часовой стрелки. В некоторых случаях используется латинская литера D, которая допускается к применению наравне с основным символом.Знак диаметра в Word
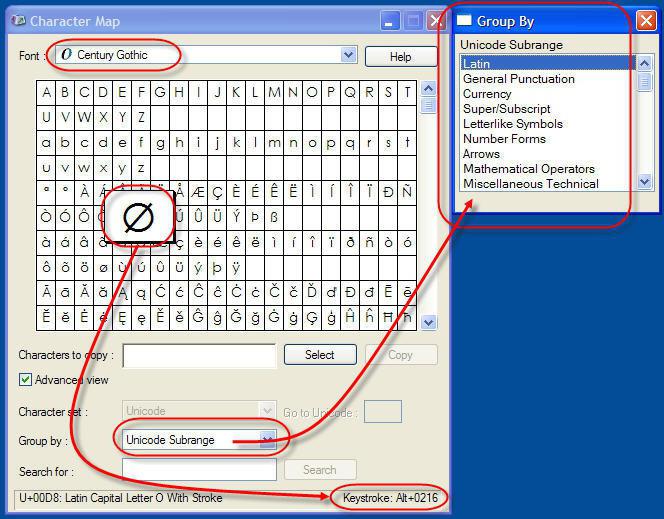
С развитием компьютерных технологий большую часть конструкторской документации начали переводить в электронную форму, что облегчает создание, хранение, пересылку и тиражирование чертежей и технологических карт. Для этого применяются специальные программы. Например, для построения чертежей используется AutoCAD, а для текстовых документов — Word, входящий в пакет Microsoft Office. Наряду с платным программным обеспечением, существует и бесплатное: NanoCAD, Open Office.
Соответственно, в эти программы перекочевали и условные обозначения, в том числе и знак диаметра. На стандартной раскладке клавиатуры он отсутствует, поэтому, чтобы вставить его в документ, создаваемый с использованием текстового редактора Word, необходимо пройти следующим путем: «Вставка → Символ → Другие символы → переключаем «Шрифт» на «Symbol» → Æ». Код знака диаметра в «Символ (шестнадцатеричный)» – 00С6. Так как этот элемент присутствует не во всех шрифтах, то его можно заменить на перечеркнутое «о»: «Ø», код — 00D8 в «Юникод (16)».