Центр тяжести швеллера и двутавра – Определение центров тяжести плоских сечений, составленных из стандартных профилей проката и из простейших геометрических фигур

Геометрические характеристики плоского поперечного сечения 4 элемента (полоса, двутавр, швеллер уголок) 020

1) Выписываем из таблицы сортамента (ГОСТ 8240-72, ГОСТ 8239-72 и ГОСТ 8509-86) необходимые геометрические характеристики для швеллера, двутавра, уголка и вычисляем по формулам прямоугольника:

а) Полоса (прямоугольник) 300Х24

 

б) Швеллер №20

 

в) Двутавр №24

 

г) Уголок 140Х9

 

2) Определяем положение центра тяжести сечения относительно начальных осей (осей полосы)

На отдельном листе бумаги в масштабе чертим схему поперечного сечения (рис. 2) и указываем положение центральных осей каждого элемента. Выполняем привязку (указываем расстояния) центров тяжести каждого элемента относительно начальных осей

Координаты центров тяжести элементов в осях

см,

см,

см,

см,

см,

см.

Рис. 2

Площадь поперечного сечения:

см ²,

Координаты центра тяжести сечения:

см,

см.

Откладываем на рисунке координаты и с учетом знаков, обозначаем положение центра тяжести (точка С) и проводим центральные оси

Контролируем достоверность определения положения центра тяжести сложного сечения. Для этого вычисляем координаты центров тяжести элементов сечения в координатных осях и (расстояния между собственными центральными осями отдельных элементов и центральными осями сечения):

см, см, см, см.

см, см, см, см.

и статические моменты площади сечения относительно центральных осей:

см ³,

погрешность:

см ³,

погрешность:

3) На основании формул параллельного перехода вычисляем моменты инерции сечения относительно центральных осей и

— осевые

см ⁴,

см ⁴,

— центробежный

см ⁴.

Понравилась статья! Поддержи проект! Ставь ЛАЙК!

Задача 1 | ПроСопромат.ру

Требуется определить положение главных центральных осей и величины главных центральных моментов инерции.

Сечение имеет сложную форму, состоит их 4^х простых фигур:

I – швеллера №30^а,

II – прямоугольника 2×40см,

III – двутавра №20^а,

IV – равнобокого уголка №12 (d=10мм).

Всё начинается с подготовки исходных данных. С этой целью необходимо сделать выписки из таблиц Сортамента прокатных сечений (см. рубрику «Таблицы»).

Этап 0. Подготовительный

Фигура I. Швеллер №30^а

Фигура II – прямоугольник 2×40см, В сортаменте прокатной стали этой фигуры нет, поскольку все геометрические характеристики ее свободно вычисляются

Фигура III. Двутавр №20^а.

Фигура IV. Равнобокий уголок №12 (d=10мм).

Пользуясь данными сортамента, на схеме сечения, вычерченной в достаточно крупном масштабе, показываем положение

центров тяжести каждой из фигур и собственные центральные оси х_i, у_i.

Этап 1. Определение положения центра тяжести сечения. Сечение не имеет осей симметрии. Поэтому придётся определять две координаты центра тяжести, используя формулы:

Для реализации этих формул выбираем вспомогательные оси х‘ и у‘ (см.схему сечения).

Площади отдельных фигур:

А₁=43,89см², А₂=2×40=80см²,

А₃=35,5см², А₄=23,3см².

Координаты центров тяжести отдельных фигур:

Площадь всего сечения А=182,7см².

Тогда координаты собственных центров тяжести отдельных фигур в системе случайных центральных осей

х_с, у_сбудут:

а₁=2,66см,                            b₁=-7,5см

а₂=-2,34см,                           b₂=-1,93см

а₃=-7,34см,                           b₃=9,07см

а₄=14,33см,                           b₄=2,4см.

Этап 2.  Определение моментов инерции относительно случайных центральных осей  х_с, у_с

.

Справочные сведения о знаке собственного центробежного момента инерции уголка (равнобокого и неравнобокого):

Справочные сведения для определения собственного центробежного момента инерции неравнобокого уголка:  

Этап 3. Определение положения главных центральных осей

Положительный угол  α₀ соответствует повороту против часовой стрелки главных осей относительно случайных (см.схему).

Этап 4. Определение величин главных центральных моментов инерции

Правило: Ось с максимальным главным моментом инерции «тяготеет» к более тяжелой случайной оси.

 Поэтому в нашем случае:

тогда 

 

Проверки.

1. Выполнение закона суммы осевых моментов инерции.

Для этого сравним

.

 

получаем:

Разница в последней цифре дает незначительную погрешность <<5%, что вполне допустимо в инженерных расчетах.

2. Проверка правильности вычислений.

Суть ее в том, что если все сделано правильно, то центробежный момент инерции сечения относительно найденных нами главных осей должен равняться нулю.

Подставляя сюда  

 и sin13˚20’=0,2306,                                                    cos13˚20’=0,9730,имеем

погрешность составляет:

И эта проверка выполняется.

 

 

Задача 3

Для заданных сечений, состоящих из прокатных профилей и полосы b×h, определить положение центра тяжести.

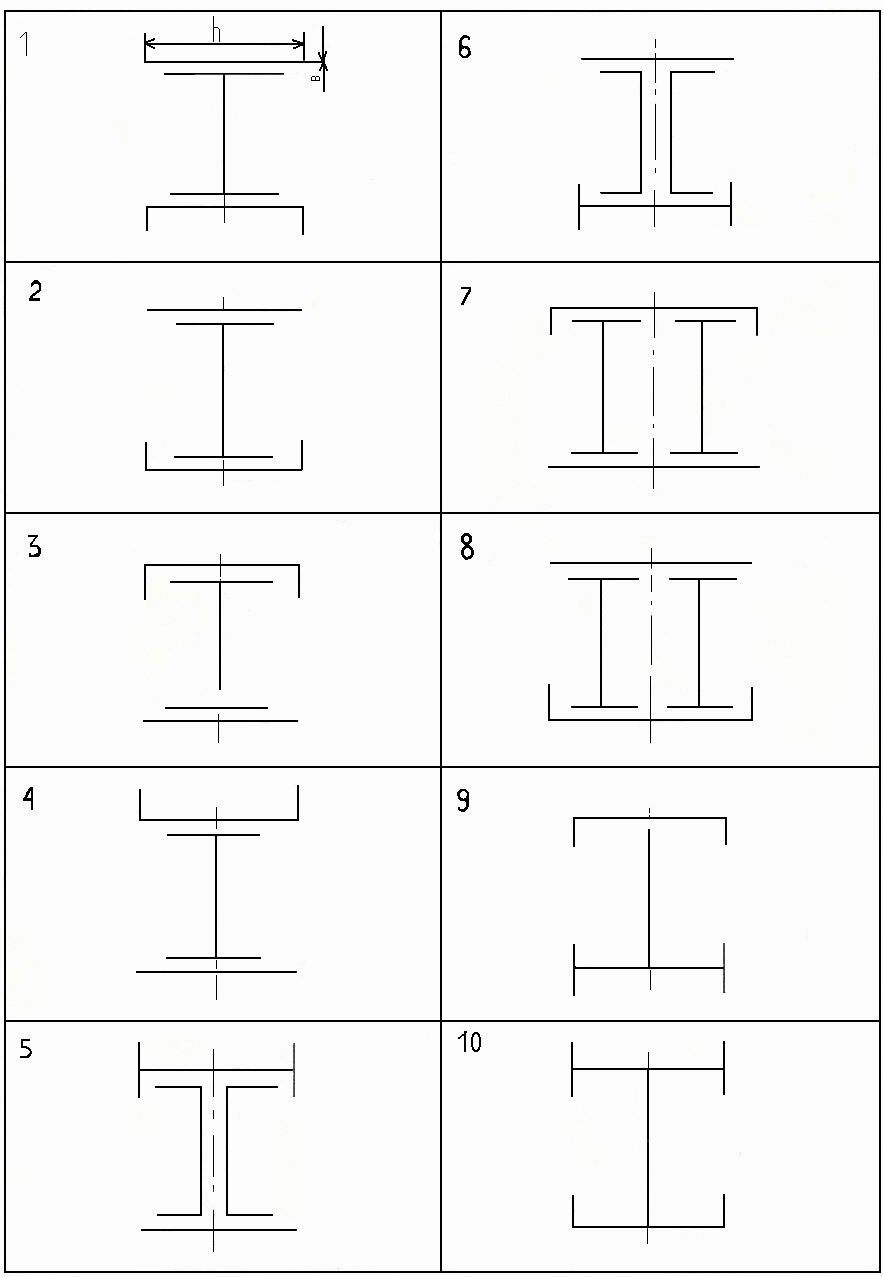
Вариант	Двутавр	b, см	h, м	Швеллер
1	12	20,0	1,2	14
2	14	18,0	1,5	16
3	16	24,0	1,8	20
4	18	28,0	2,0	18а
5	20	24,0	1,8	22а
6	22	20,0	1,5	24а
7	24	15,0	1,2	30
8	24а	12,0	1,0	33
9	18а	24,0	2,0	22
10	22а	21,0	2,4	24

ПРИМЕР 3.

Определить координаты центра тяжести сечения. Сечение состоит из двутавра № 18, швеллера № 18 и пластины 200*60 (рисунок-6)

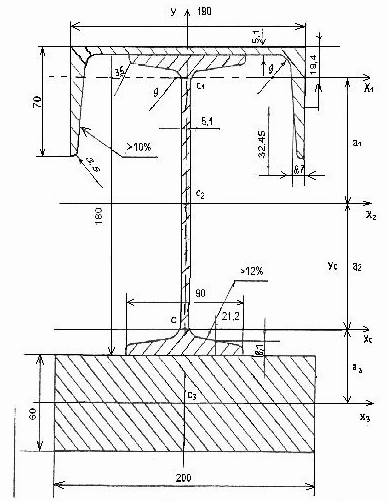
Рисунок — 6

1. Разобьем сечение на профили проката. Оно состоит из двутавра № 18, швеллера № 18 и пластины 200*60. обозначим их 1, 2, 3.

2. Укажем центры тяжести каждого профиля, используя таблицу приложения, и обозначим их С₁, С₂, С₃, проведем через них оси Х₁, Х₂, Х₃.

3. Выберем систему координатных осей. Ось Yсовместим с осью симметрии, а ось Х проведем через центр тяжести двутавра.

4. Определим центр тяжести всего сечения. Так как ось Yсовпадает с осью симметрии, то она проходит через центр тяжести сечения, потому Хс=0. КоординатуYс определим по формуле:

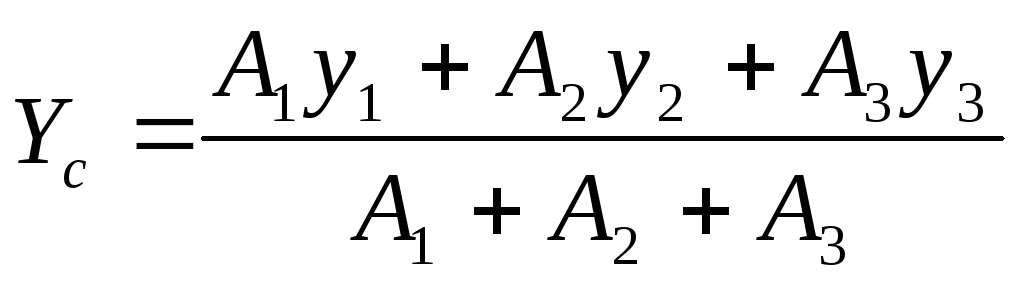
Пользуясь таблицами ГОСТ 8239-89, ГОСТ 8240-89, ГОСТ 8510-86, ГОСТ 8509-86, определим координаты центров тяжести

А₁ = 20,7 см²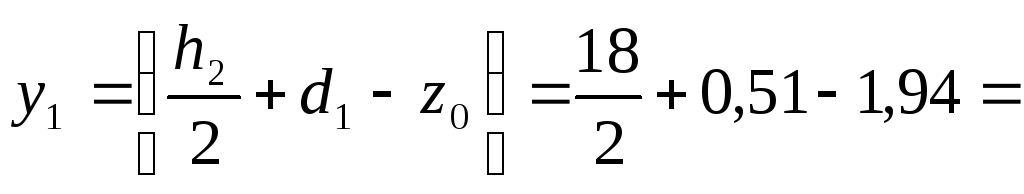7,57 см

А₂ = 23,4 см²y₂ = 0

А₃ = 20*6 = 120 см² 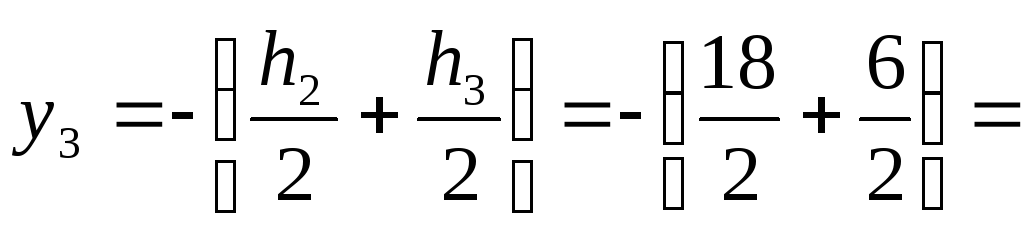-12 см

Координата у₂ равна нулю, так как ось Х проходит через центр тяжести двутавра. Подставим полученные значения в формулу для определения у_С:

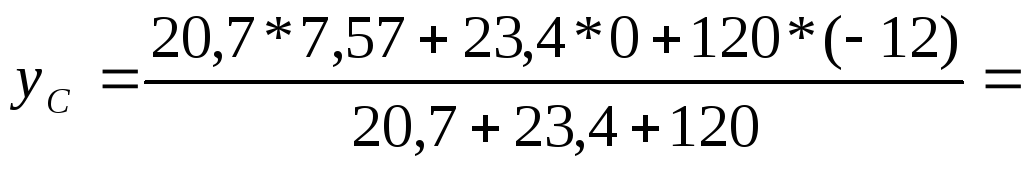-7,82 см

1. Укажем центр тяжести сечения на рисунке и обозначим его буквой С. Покажем расстояние у_С = -7,82 см от оси Х до точки С.

2. Определим расстояние между точками С и С₁, С и С₂, С и С₃, обозначим их а₁, а₂, а₃:

а₁ = у₁ + у_С = 7,57 + 7,82 = 15,39 см

а₂ = у_С = 7,82 см

а₁ = у₃ — у_С = 12 — 7,82 = 4,18 см

3. Выполним проверку. Для этого ось Х проведем по нижнему краю пластины. Ось Y оставим, как в первом решении. Формулы для определения х_С и у_С не изменятся:

х_С = 0,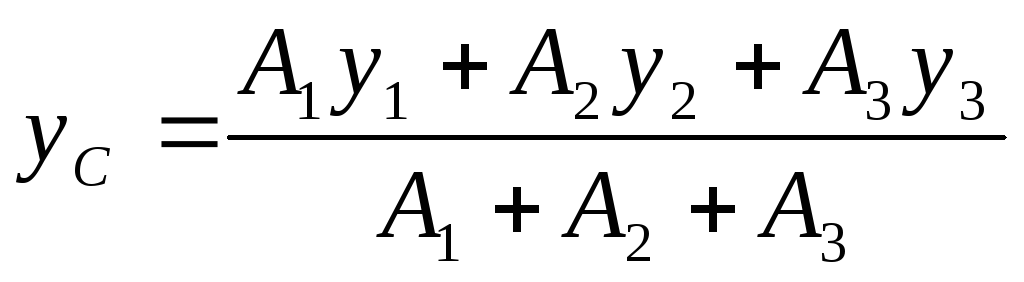

Площади профилей останутся такими же, а координаты центров тяжести двутавра, швеллера и пластины изменятся.

А₁ = 20,7 см²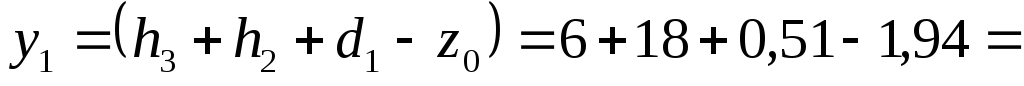22,57 см

А₂ = 23,4 см²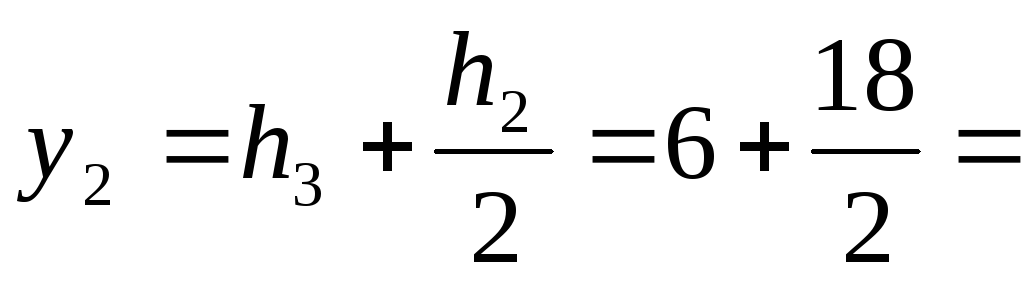 15 см

А₃ = 20*6 = 120 см² 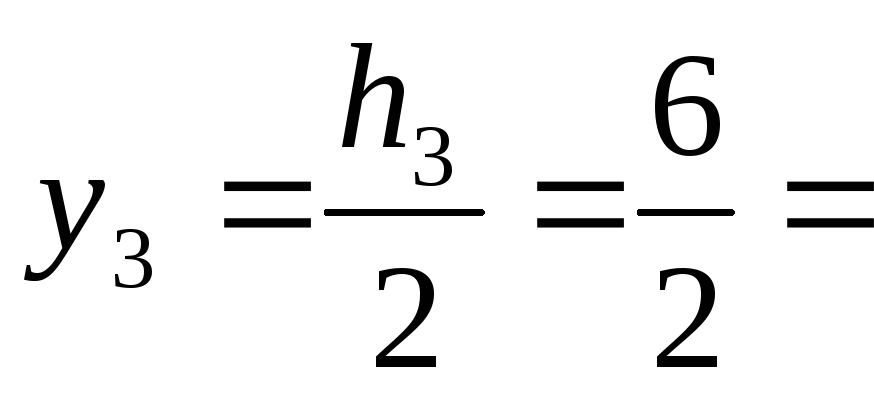3 см

Находим координату центра тяжести:

7,18 См

По найденным координатам х_С и у_С наносим на рисунок точку С. Найденное двумя способами положение центра тяжести находится в одной и той же точке. Сумма координат у_С, найденных при первом и втором решении: 7,82 + 7,18 = 15 см

Это равно расстоянию между осями Х при первом и втором решении:

18/2 + 6 = 15 см.

ЗАДАЧА 4

По оси ступенчатого бруса приложены силы и 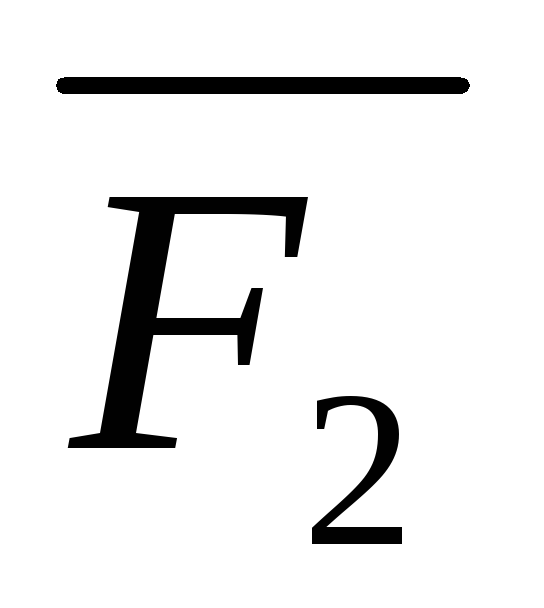. Необходимо построить эпюры продольных сил и нормальных напряжений, определить абсолютную деформацию бруса. Принять Е = 2,1 * 10⁵ МПа.

Вариант	F1, кН	F2, кН	l1, м	l2, м	l3, м	А, см2
1	20	30	1,0	1,2	1,4	4,0
2	50	40	1,2	1,4	1,6	6,0
3	20	40	1,4	1,6	1,8	3,5
4	60	20	1,6	1,8	2,0	4,5
5	25	35	1,8	1,6	1,4	4,0
6	35	55	2,0	1,4	1,2	6,5
7	40	60	1,8	2,0	2,4	7,5
8	50	40	1,6	1,4	1,2	6,0
9	30	50	1,4	1,2	1,0	5,0
10	15	40	1,2	1,4	1,6	4,0

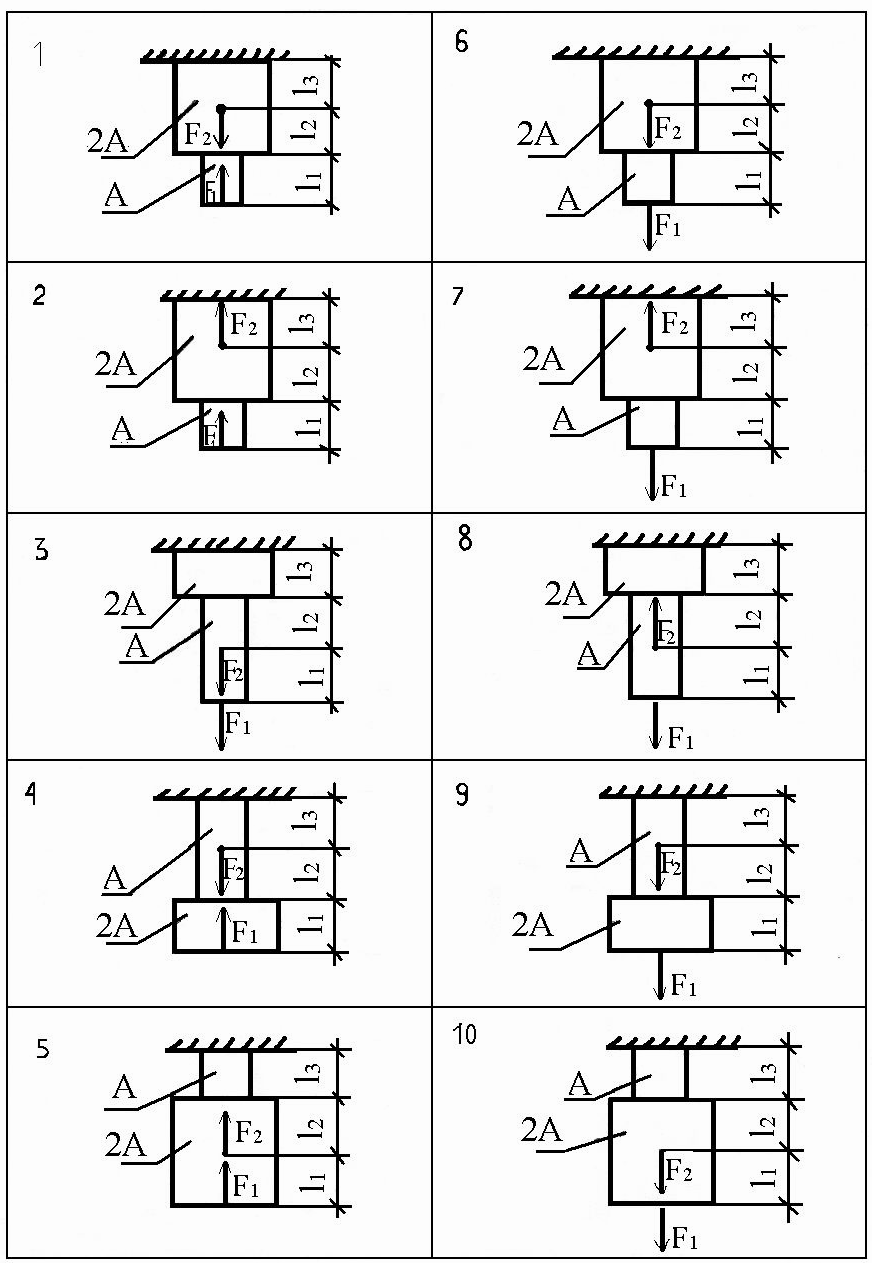
ПРИМЕР 4

Для данного ступенчатого бруса построить эпюры продольных сил и нормальных напряжений. Определить абсолютное удлинение (укорочение) бруса (рисунок 7)

Дано:

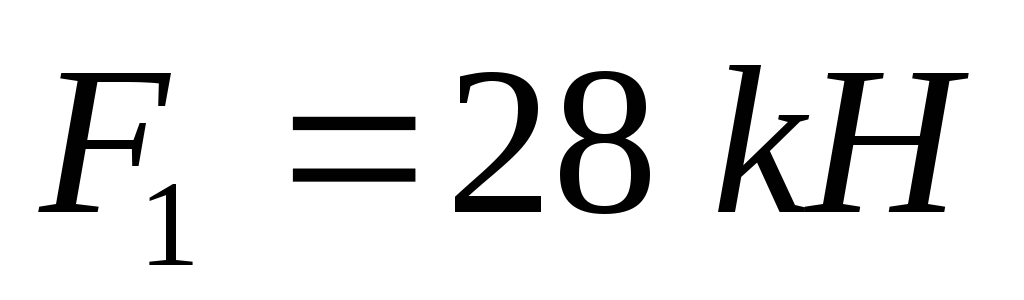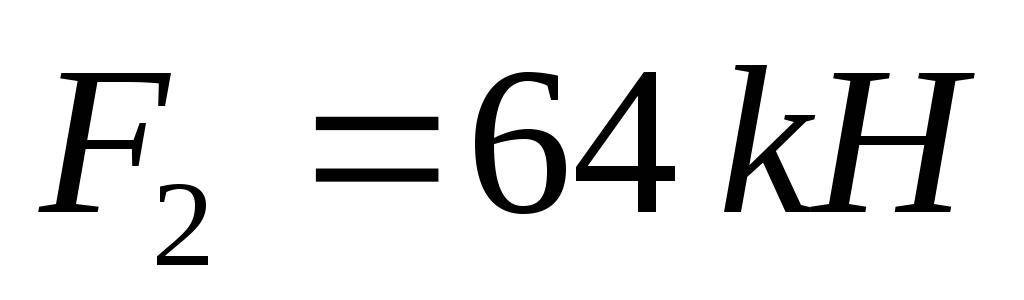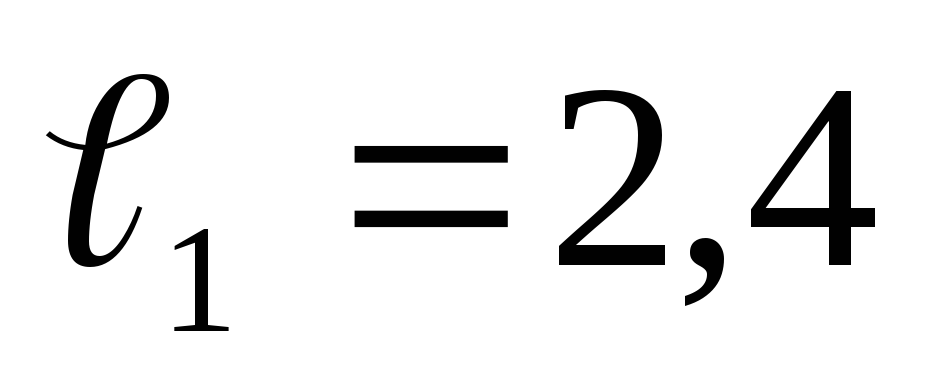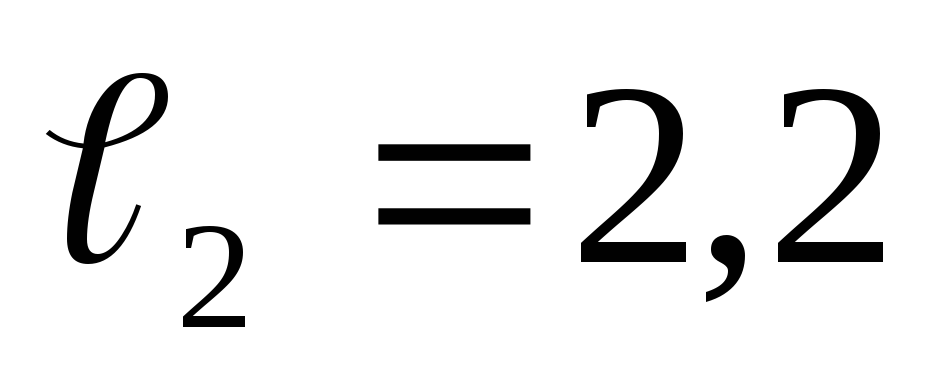, ,м,м,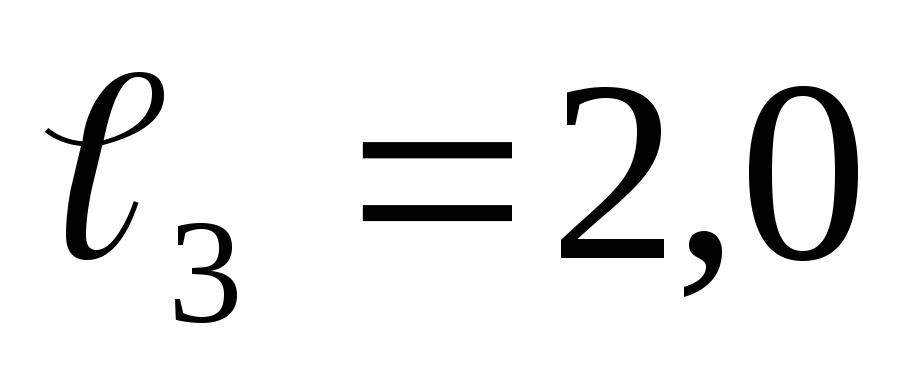м, А=3,2 см², Е=2,1*10⁵МПа

36

112.5

N₃

—

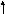
3

3

­_

_

—

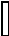
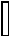
36

F₂

F₂

43,75

—

28

N₂

112,5

2

43.75

—

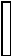
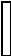
87,5

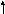
28

87,5

F₁

—

F₁

—

Эпюра N_Z(кН)

Эпюра σ (МПа)

—

—

Z

Z

Рисунок — 7

Решение

1 Проводим ось Zв сторону свободного конца бруса и определяем реакцию заделки:

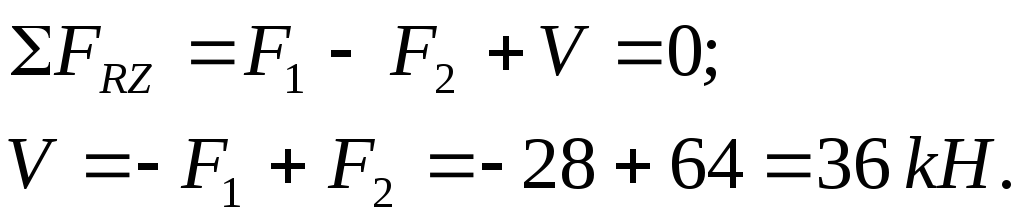
2 Разбиваем брус на участки, границы которых определяются сечениями, где изменяется площадь поперечного сечения или приложены внешние силы. На каждом из участков проводим характерные сечения 1-1, 2-2, 3-3. С помощью метода сечений определяем продольные силы на каждом из участков бруса: мысленно рассекаем брус в пределах первого участка сечения 1-1, отбрасываем верхнюю часть бруса и заменяем ее действие продольной силой N₁(рисунок 7) для оставшейся части составляем уравнение равновесия:

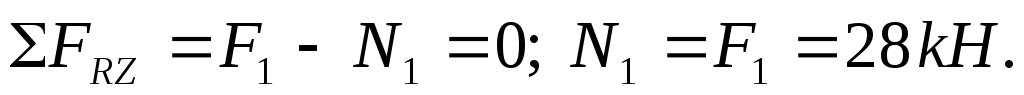
Аналогично находим N₂иN₃:

сечение 2-2 (рисунок 7)

;

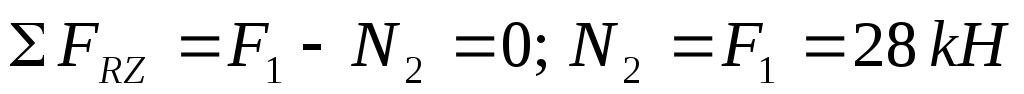сечение 3-3 (рисунок 7)

.

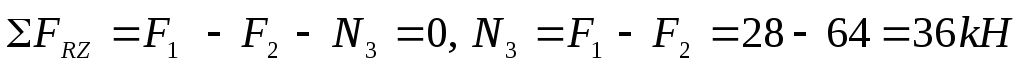По найденным значениям продольной силы строим соответствующую эпюру. Для этого параллельно оси бруса проведем базовую (нулевую) линию. Левее ее откладываем отрицательные значения N, соответствующие сжатому участку, а правее – положительные значенияN, соответствующие растянутому участку (рисунок — 7).

Определяем нормальные напряжения в характерных сечениях бруса по формуле: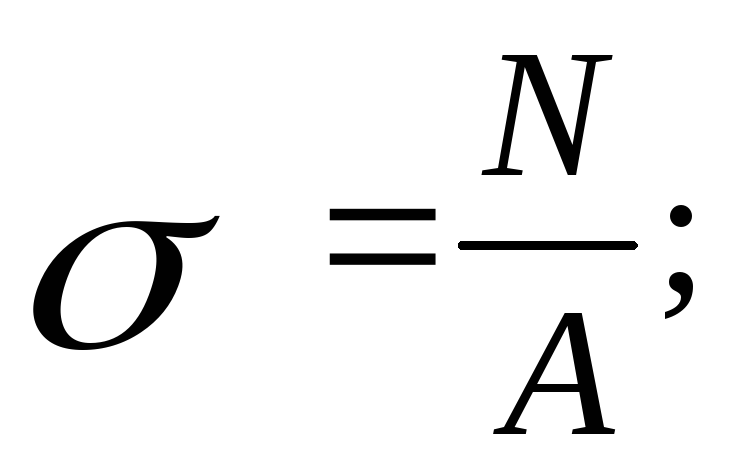

;

.

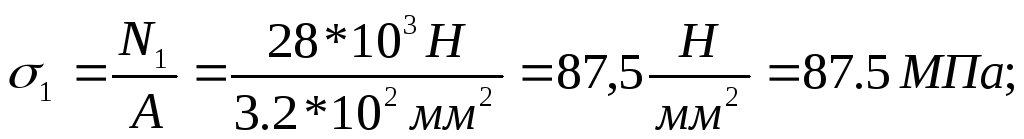
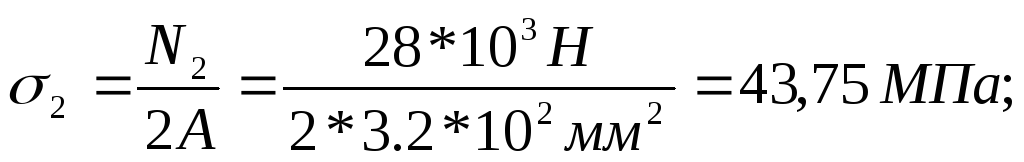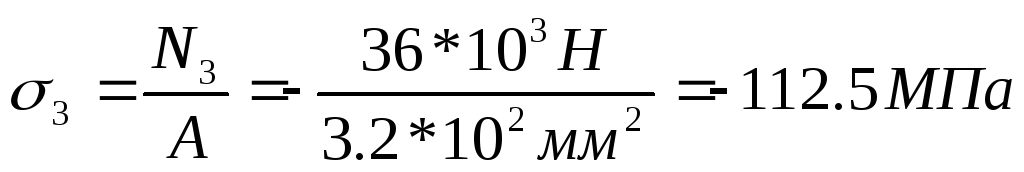Строим соответствующую найденным значениям эпюру σ (рисунок — 7)

4 Определяем абсолютное удлинение бруса.

В соответствии с законом Гука:

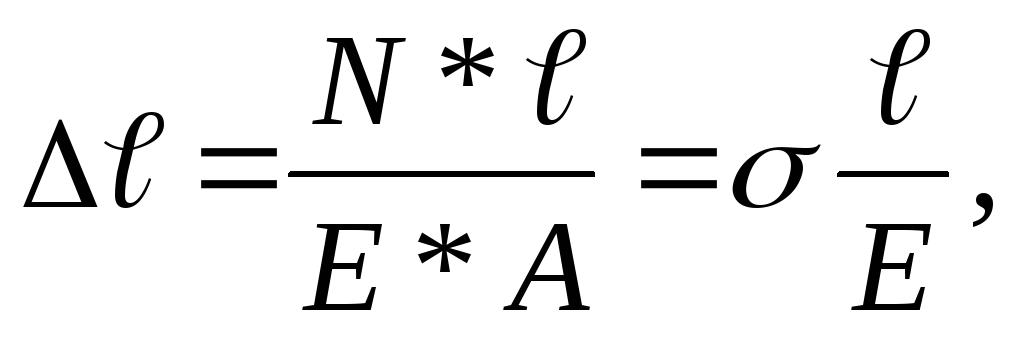
где Е=2,1*10⁵МПа – модуль продольной упругости для стали.

Складывая удлинение участков, получим:

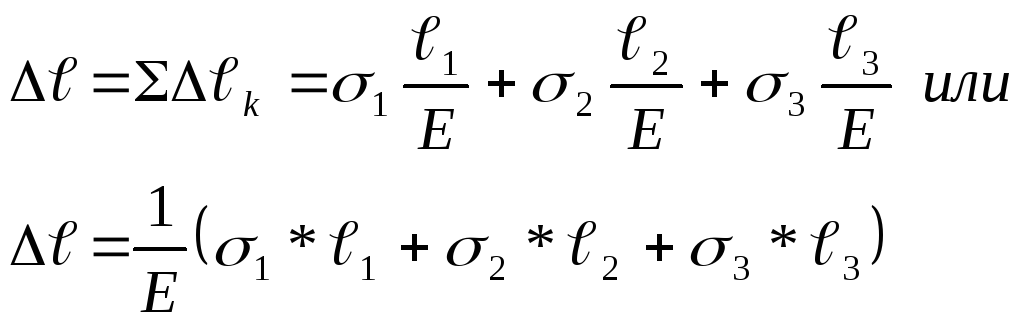
Учитывая, что Iм=10³мм, будем иметь:

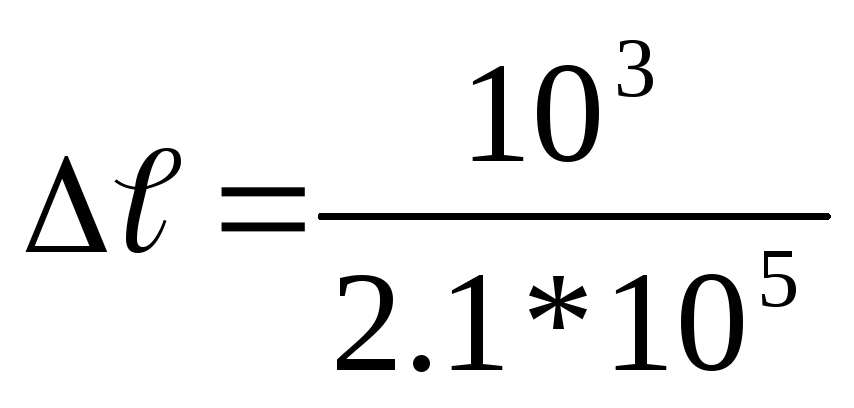(87,5*2,4+43,75*2,2-112,5*2,0)=0,39 мм.

Таким образом, абсолютное удлинение бруса = 0,39 мм.

ЗАДАЧА 5

По данным задачи 2 для двухопорной балки построить эпоры поперечных сил Qу и изгибающих моментов М_х. Подобрать сечение стального двутавра, приняв

[σ] = 160 МПа.

ПРИМЕР 5

Для двухопорной балки построить эпюры поперечных сил Qи изгибающих моментов М. Подобрать сечение стального двутавра, приняв [σ] = 160 МПа.

Дано: F₁=24kH;F₂=36 кН;m₁=18 кНм;

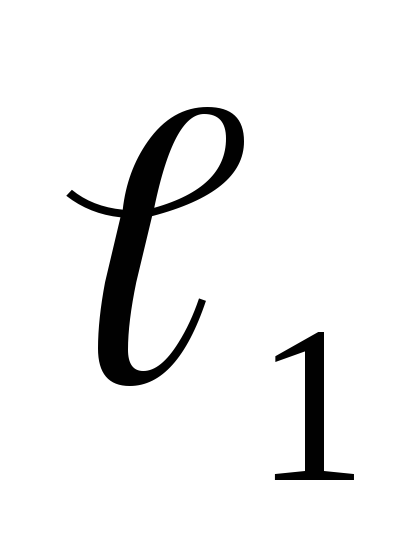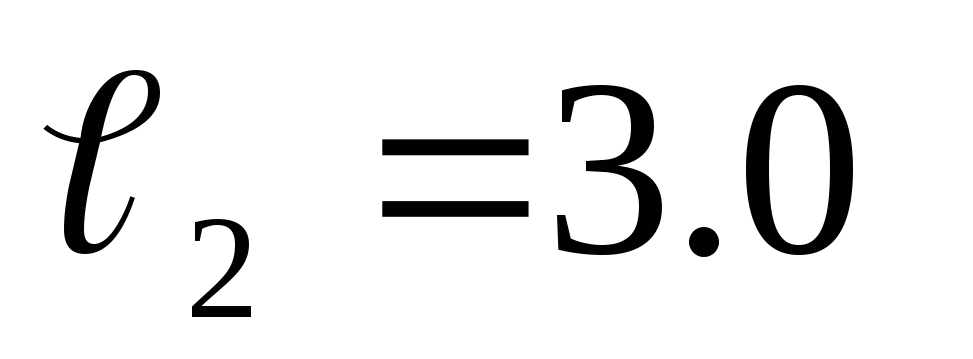m₂=24 кНм;=2.0 м;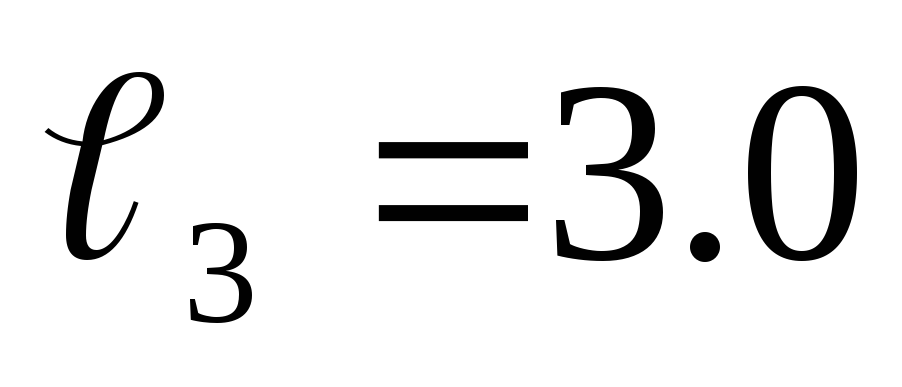м;м.

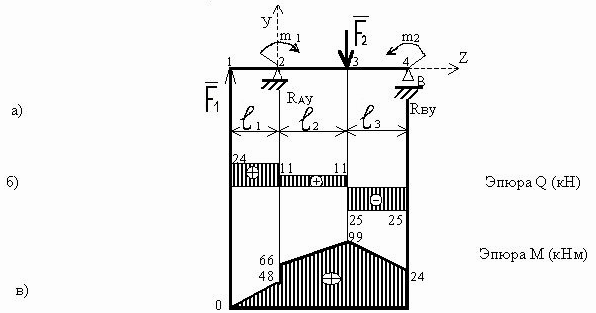
Рисунок — 8

Решение

1 Составляем уравнение равновесия параллельной системы сил, из которых определяем опорные реакции балки:

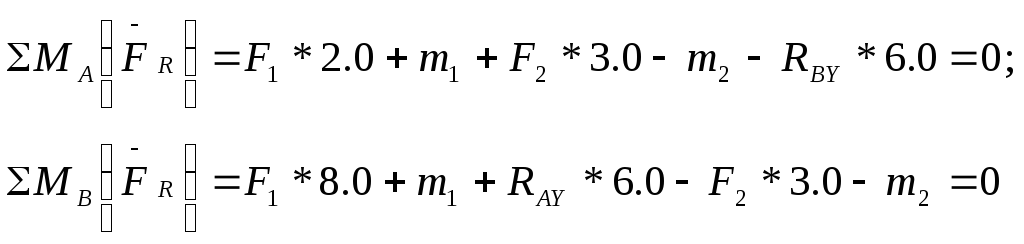
(5)

₍₆₎

Из уравнения (6) находим R_AУ:

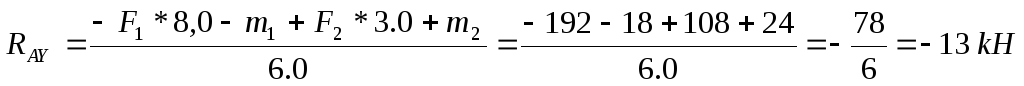
Из уравнения (5) находим В:

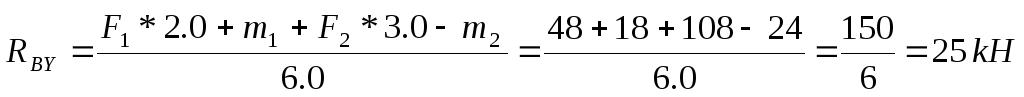
Проверяем правильность определения опорных реакций, составляя сумму проекций всех сил на ось У:

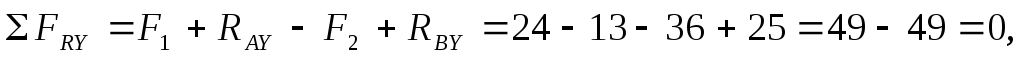
то есть реакции определены верно.

2 Определяем значения поперечной силы Qв характерных сечениях балки, которые обозначим цифрами 1, 2, 3, 4 (рисунок 8 а)

Q₁=Q₂^лев=F₁=24 кН;

Q₂^прав=Q₃^лев=F₁+R_АУ=24-13=11 кН;

Q₃^2прав=Q₄=F₁+R_АУ-F₂= -R_ВУ= -25 кН.

По найденным значениям строим эпюру, поперечных сил Q(рисунок 8 б).

3 Аналогично определяем значения изгибающего момента М в характерных сечениях балки:

М₁=0;

М₂^лев=F₁*2.0=48 кНм

М₂^прав=М₂^лев+m₁=48+18=66 кНм;

М₃=F₁*5.0+m₁+R_АУ*3,0=120+18-39=99 кНм;

М₄=m₂=24 кНм.

По найденным значениям строим эпюру изгибающих моментов М (рисунок 8 в).

4 По эпюре изгибающих моментов определяем положение опасного сечения балки (сечение, в котором изгибающий момент имеет наибольшее по абсолютной величине значение). В нашем случае – это сечение 3, где М₃=М_maх=99 кНм. Из условия прочности балки на изгиб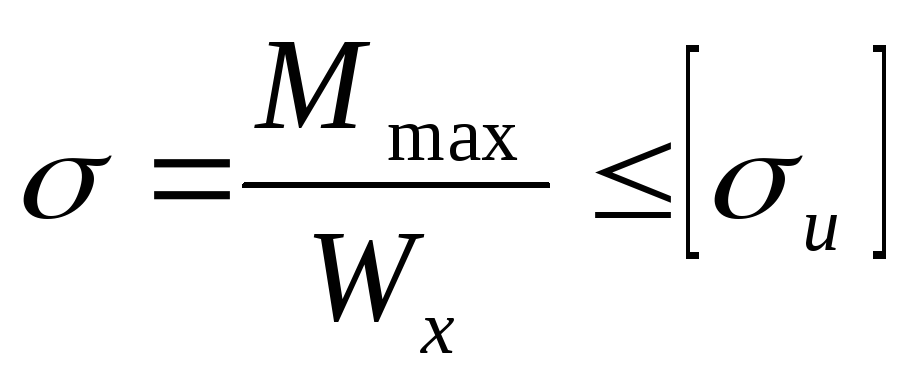вычисляем необходимый осевой момент сопротивления:

.

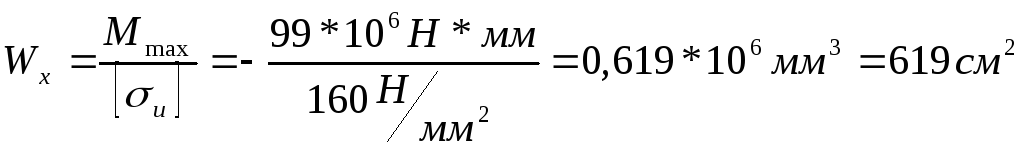В соответствии с ГОСТ 8239-89 принимаем сечение из стального двутавра № 33 с Wх=597 см³. Имеем перенапряжение:

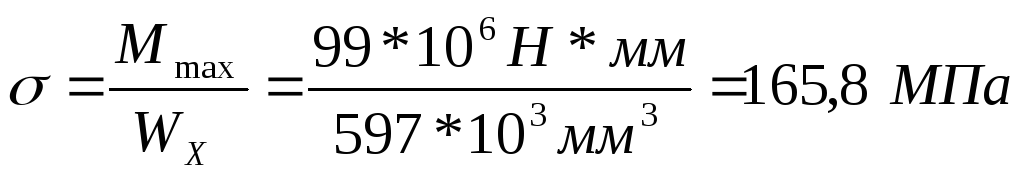
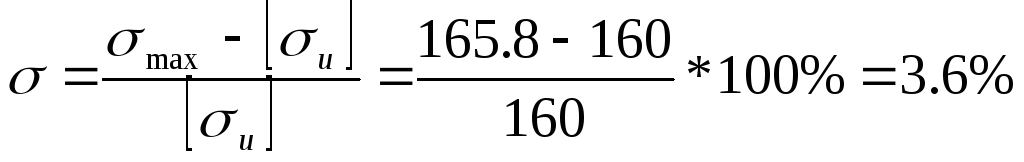
< 5%

что находится в разрешенных пределах (менее 5%).

Ответ: сечение балки двутавр № 33.

36

Задачи на геометрические характеристики | ПроСопромат.ру

Требуется определить положение главных центральных осей и величины главных центральных моментов инерции.

Сечение имеет сложную форму, состоит их 4^х простых фигур:

I – швеллера №30^а,

II – прямоугольника 2×40см,

III – двутавра №20^а,

IV – равнобокого уголка №12 (d=10мм).

Всё начинается с подготовки исходных данных. С этой целью необходимо сделать выписки из таблиц Сортамента прокатных сечений (см. рубрику «Таблицы»).

Этап 0. Подготовительный

Фигура I. Швеллер №30^а

Фигура II – прямоугольник 2×40см, В сортаменте прокатной стали этой фигуры нет, поскольку все геометрические характеристики ее свободно вычисляются

Фигура III. Двутавр №20^а.

Фигура IV. Равнобокий уголок №12 (d=10мм).

Пользуясь данными сортамента, на схеме сечения, вычерченной в достаточно крупном масштабе, показываем положение центров тяжести каждой из фигур и собственные центральные оси х_i, у_i.

Этап 1. Определение положения центра тяжести сечения. Сечение не имеет осей симметрии. Поэтому придётся определять две координаты центра тяжести, используя формулы:

Для реализации этих формул выбираем вспомогательные оси х‘ и у‘ (см.схему сечения).

Площади отдельных фигур: А₁=43,89см², А₂=2×40=80см²,

А₃=35,5см², А₄=23,3см².

Координаты центров тяжести отдельных фигур:

Площадь всего сечения А=182,7см².

Тогда координаты собственных центров тяжести отдельных фигур в системе случайных центральных осей х_с, у_сбудут:

а₁=2,66см,                            b₁=-7,5см

а₂=-2,34см,                           b₂=-1,93см

а₃=-7,34см,                           b₃=9,07см

а₄=14,33см,                           b₄=2,4см.

Этап 2.  Определение моментов инерции относительно случайных центральных осей  х_с, у_с.

Справочные сведения о знаке собственного центробежного момента инерции уголка (равнобокого и неравнобокого):

Справочные сведения для определения собственного центробежного момента инерции неравнобокого уголка:  

Этап 3. Определение положения главных центральных осей

Положительный угол  α₀ соответствует повороту против часовой стрелки главных осей относительно случайных (см.схему).

Этап 4. Определение величин главных центральных моментов инерции

Правило: Ось с максимальным главным моментом инерции «тяготеет» к более тяжелой случайной оси. Поэтому в нашем случае:

тогда 

 

Проверки.

1. Выполнение закона суммы осевых моментов инерции.

Для этого сравним

.

 

получаем:

Разница в последней цифре дает незначительную погрешность <<5%, что вполне допустимо в инженерных расчетах.

2. Проверка правильности вычислений.

Суть ее в том, что если все сделано правильно, то центробежный момент инерции сечения относительно найденных нами главных осей должен равняться нулю.

Подставляя сюда    и sin13˚20’=0,2306,                                                    cos13˚20’=0,9730,имеем

погрешность составляет:

И эта проверка выполняется.

 

 

5.3 Положение центров тяжести профилей проката

ГОСТ 8239 — 89: ДВУТАВРЫ СТАЛЬНЫЕ ГОРЯЧЕКАТАНЫЕ

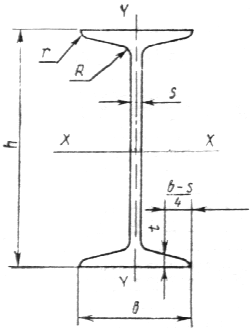
h — высота двутавра;

b — ширина полки;

s — толщина стенки;

t — средняя толщина полки;

С – центр тяжести (на пересечении осей y – y и х – х)

Номер двутавра определяется высотой h. Например у двутавра №10 — h = 100мм

С

ГОСТ 8240-89 ШВЕЛЛЕРЫ СТАЛЬНЫЕ ГОРЯЧЕКАТАНЫЕ

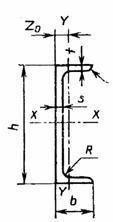
h — высота;

b — ширина полки;

s — толщина стенки;

t — толщина полки;

z₀ — расстояние от оси y — y до наружной грани стенки.

С – центр тяжести (на пересечении осей y – y и х – х)

Номер швеллера определяется высотой h. Например у швеллера №12 — h = 120мм

С

ГОСТ 8510 – 72 СТАЛЬ ПРОКАТНАЯ УГЛОВАЯ НЕРАВНОПОЛОЧНАЯ

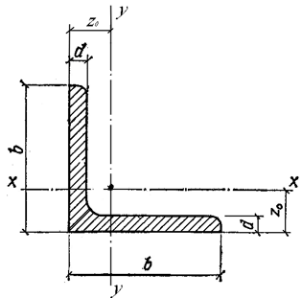
b — ширина полки;

d — толщина полки;

z₀ — расстояние от центра тяжести до полки

С – центр тяжести (на пересечении осей y – y и х – х)

Обозначение уголка определяется шириной (b) и толщиной (d) полки. Например, уголок №5 (или 504) b = 50мм, d = 4 мм.

С

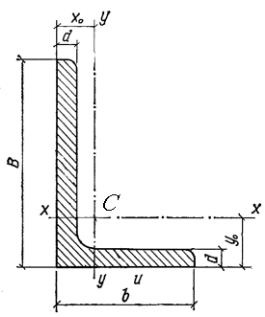
ГОСТ 8509 – 72 СТАЛЬ ПРОКАТНАЯ УГЛОВАЯ РАВНОПОЛОЧНАЯ

В – ширина большой полки

b — ширина малой полки;

d — толщина полки;

х₀, у₀ — расстояния от центра тяжести до наружных граней полки

С – центр тяжести (на пересечении осей y – y и х – х)

Обозначение уголка определяется размерами В, b, d. Например уголок № 7,5/5 (или 75505): В= 75 мм, b= 50мм,d = 5 мм.

Определение центров тяжести плоских сечений, составленных из стандартных профилей проката и из простейших геометрических фигур

Тема:Центр тяжести.

Цель работы: научить определять центр тяжести сложных сечений.

1. Разбивают сечение на простые фигуры. В задачах такими фигурами являются стандартные профили проката. Обычно профили прокатной стали, образующие сечение, обозначают цифрами 1,2,3… .

2. Указывают центры тяжести каждого профиля (фигуры) и обозначают их С¹, С₂…, С_n, используя таблицы ГОСТОв (см. прилож.1.)

3. Выбирают систему координатных осей. Рекомендуется одну из координатных осей совмещать с осью симметрии. Вторую ось координат направляют перпендикулярно первой так, чтобы она пересекла центры тяжести одной или нескольких фигур. При этом начало координат может совпадать (или не совпадать) с центром тяжести из фигур. Вторую ось можно направить так, чтобы она прошла через нижнюю (крайнюю) точку сечения. В первом случае вычисления будут более простыми.

4. Составляют формулы для определения координат центра тяжести сечения:

 

1) х_с = ;

2) у_с = .

Пользуясь таблицами ГОСТов (см. прилож. 1), определяют площади профилей проката А₁, А₂…, А_n, координаты их центров тяжести х₁, х_2,…х_n и у₁, у_2,…у_n относительно выбранных осей координат. Число слагаемых в числите и знаменателе формул зависит от числа профилей, из которых состоит сечение. Полученные величины подставляют в формулу и находят х_с и у_с.

Следует помнить, что если ось х совмещена с осью симметрии, то координата у_с = 0, а если ось у совмещена с осью симметрии, то х_с =0.

5. Указывают положение центра тяжести на рисунке, придерживаясь определенного масштаба, и показывают расстояние от центра тяжести до координат осей.

6. Выполняют проверку правильности решения, для чего можно изменить положение координатных осей (или одной оси) и найти координаты центра тяжести относительно новых осей. Положение центра тяжести не зависит от того, как выбрана система координатных осей.

Пример 3.1. Определить координаты центра тяжести сечения, составленного из профилей проката, как показано на рис.3. Сечение состоит из двутавровой балки № 33, швеллера № 27, двух уголков 90х56х6 мм и листа сечением 12х180 мм.

Решение 1.Разобьем сечение в соответствии с профилями проката и обозначим их 1,2,3,4,5.

2. Пользуясь таблицей укажем центры тяжести каждого профиля и обозначим их С₁, С₂, С₃, С₄, и С₅.

3. Выберем систему осей координат. Ось у совместим с осью симметрии, а ось х направим перпендикулярно оси у и проведем через центр тяжести двутавровой балки.

4. Выпишем формулы для определения координат центра тяжести сечения:

х_с = 0, так как ось у совпадает с осью симметрии;

 

у_с = .

Учитывая, что А₂ = А₃, а также, что у₂ = у_3, получим:

у_с = .

Определим площади и координаты центров тяжести отдельных профилей проката, используя сечение и таблицы 2,3,4 прилож. 1

А₁ = 35,2 см²; А₂ = А₃= 8,54 см²; А₄ = 53,8 см²;

А₅ = 1,2 ·18 = 21,6 см²;

у₁ = h_дв/2 + d_шв –z_0(шв) =

у₂ = у₃ = h_дв/2 + d_шв – b_шв + х_0(уг) =

у₄ = 0, так как ось х проходит через центр тяжести двутавра;

у₅ = — (h_дв/2 + δ_листа/2) = —

Рис. 3

Поставим полученные значения в формулу для определения у_с:

 

у_с =

Укажем положение центра тяжести сечения С (см рис. 3 а).

5. Проверка решения. Проведем ось х по нижней грани листа (рис. 3 б.). Площади профилей останутся теми же, а координаты центров тяжести изменятся:

 

у₁ = δ_листа + h_дв + d_шв – z_0(шв) = 1,2 + 33 + 0,6 – 2,47 = 32,33 см;

у₂ = δ_листа + h_дв + d_шв – b_шв – х_0(уг) = 1,2 + 33 + 0,6 – 9,5 — 1,28 = 26,58 см;

у₂ = у₃ = 26,58 см;

у₄ = δ_листа + h_дв/2 = 1,2 +

у₅ = δ_листа /2 = .

Определим положение центра тяжести в новой системе координат

 

у_с =

Разность между координатами центра тяжести должна быть равна расстоянию между осями х в первом и во втором решении:

20,3 – 2,33 = + 1,2,

откуда 17,7 см = 17,7 см.

Ответ: у_с = 2,33 см, если ось х проходит через С₄ , и у_с = 20,03 см, если ось х проходит по нижней грани.

 

 

Продолжение таблицы № 1

 

 

 

Продолжение таблицы № 2

 

 

 

Таблица 3

 

 

Список литературы

 

 

1. А.И. Аркуша «Техническая механика». Высшая школа 2003.

2. В.Э. Зависновский, Н.М. Захаров. «Техническая механика» ООО «Амалфея» 2000 г.

3. В.И. Сетков. Сборник задач по технической механике». М.: 2003.

 

характеристики и сравнение балок по прочности и другим свойствам. Двутавры и швеллеры

Это объясняется механическими характеристиками этих открытых незамкнутых профилей, отлично подходящими для восприятия локальных и распределенных нагрузок, и отработанным технологическим процессом их производства.

Форма геометрического сечения двутавра и швеллера имеет большую площадь, расположенную в полках. А области возникновения максимальных напряжений в двутаврах и швеллерах от изгибающей нагрузки сосредоточены именно в полках. Рациональность этих профилей объясняется наиболее эффективным использованием материала и снижением веса конструкции.

Основным отличием свойств швеллера и двутавра является различная реакция на скручивающую силу, которая может возникнуть даже в симметричном относительно двух плоскостей двутавровом профиле при определенном распределении нагрузки на перекрытие.

Двутавры

Максимальный объем металла в двутавровом профиле распределен в полках. Именно в них и возникают напряжения от приложенных нагрузок (в том числе, сжимающих, скручивающих и изгибающих). Кроме того, полки двутавра разнесены на такое расстояние, при котором момент инерции становится максимальным. Этим объясняется высокая величина момента инерции этого профиля, который для двутаврового профиля 16 достигает 2,6 т/м (при изгибе).

Несмотря на симметричность профиля, двутавровая балка может испытывать деформацию кручения, например, при опирании на нее перекрытия, неравномерно загруженного полезной нагрузкой.

Недостатком двутавра является его более высокая стоимость, чем у швеллера. Поэтому применять его целесообразно в гражданском, промышленном или другом масштабном строительстве, а также для перекрытий, работающих под значительной нагрузкой.

Швеллеры

Геометрическая форма швеллерного профиля обусловливает несовпадение его главной оси инерции со стенкой. Поэтому момент инерции П-образного сечения превышает момент инерции Н-образного сечения, что предпочтительнее для косого изгиба.

При восприятии опирающейся нагрузки швеллер испытывает скручивание, поскольку ось симметрии только одна и она не совпадает с осью нагружения. В результате центр изгиба располагается за стенкой несимметричного швеллерного профиля. При этом кручение является стесненным и имеет бимомент, который следует учитывать в проектных расчетах. Также необходимо учитывать секториальную жесткость швеллера, которая в 1,5 – 2 раза выше, чем у двутавра (при одинаковых высоте стенки и ширине полки).

Из двух швеллеров можно изготовить конструкцию, механически более прочную (изгибные жесткости в разных направлениям распределены более рационально), чем двутавр таких же размеров. Эта конструкция имеет квадратное сечение (пространственная форма является коробом), образуемое свариванием швеллеров по конечным граням полок и усиленное металлическими пластинами. В результате моменты инерции относительно центральных моментов инерции такого короба выравниваются. Однако подобное решение отличается трудоемким изготовлением.

Главное преимущество швеллера перед двутавром – меньшая стоимость при аналогичных механических и геометрических параметрах. Его целесообразно использовать в легких конструкциях: частных одно- или двухэтажных домах, гаражах, дачах и т. д.

Однако применение в перекрытии швеллера потребует крепления, чтобы обеспечить устойчивость этого профиля (при расположении стенки в вертикальной плоскости). Противодействие неустойчивости швеллера под изгибающей нагрузкой можно обеспечить привариванием поперечных жестких элементов, бетонированием или кирпичной кладкой.

Металлопрокат в виде швеллера и двутавра применяют в разных областях: от машиностроения до создания рекламных щитов. Привлекательность балок заключена в сочетании конструкционных свойств и надежности, обусловленной формой профиля: П- и Н-образной. Благодаря этой особенности металлопрокат выдерживает существенные вертикальные и горизонтальные нагрузки, перераспределяя их по всей своей длине и обеспечивая долговечность сооружению. Что представляет собой каждый из этих материалов и какой прочнее?

Применение различных видов металлопрофиля для каркаса крыши

Особенности металлопроката швеллерного типа

Балки, имеющие в разрезе П-образное сечение, называют швеллерами. Изготавливают их методом холодной или горячей гибки.

Виды швеллерных балок и их размеры