Расчет неразрезной балки по уравнению трех моментов
Как рассчитать неразрезную балку. Уравнение 3-х моментов.
Неразрезная балка нагружена во всех пролетах. Построить эпюры Q и M для неразрезной балки.

Схема неразрезной балки
1. Определяем степень статической неопределимости балки по формуле:
n= Соп -3= 5-3 =2, где Соп – число неизвестных реакций, 3 – число уравнений статики. Для решения данной балки требуется два дополнительных уравнения.
2. Обозначим номера опор с нулевой по порядку (0,1,2,3)
3. Обозначим номера пролетов с первого по порядку (ι1,ι2,ι3)
4. Каждый пролет рассматриваем как простую балку
 — это поперечная сила и изгибающий момент для простой балки.
— это поперечная сила и изгибающий момент для простой балки.Рассмотрим балку 1го пролета


Определим фиктивные реакции для балки первого пролета по табличным формулам (см.таблицу «Фиктивные опорные реакции….»)
Балка 2го пролета


Балка 3го пролета

5. Составляем уравнение 3х моментов для двух точек – промежуточных опор – опора 1 и опора 2. Это и будут два недостающих уравнения для решения задачи.
Уравнение 3х моментов в общем виде:
Для точки (опоры) 1 (n=1):
Для точки (опоры) 2 (n=2):
Подставляем все известные величины, учитываем, что момент на нулевой опоре и на третьей опоре равны нулю, M
Тогда получим:
Поделим первое уравнение на сомножитель 4 при M2
Второе уравнение поделим на сомножитель 20 при M2
Решим эту систему уравнений:
Из первого уравнения вычтем второе, получим:
Подставляем это значение в любое из уравнений и находим M2

Итак, нашли опорные моменты:
- Построение эпюры поперечной силы Q для неразрезной балки
Формула для определения Q в любом сечении неразрезной балки:
1) Построение эп. Q в первом пролете:
 Эта запись означает, что поперечная сила в неразрезной балке в первом пролете будет такая же, как в простой балке с разницей ординат на – 9 .
Эта запись означает, что поперечная сила в неразрезной балке в первом пролете будет такая же, как в простой балке с разницей ординат на – 9 .
На эпюрах должны прослеживаться скачки на величину сил.
2) Построение эп. Q
 Поперечная сила в неразрезной балке во втором пролете будет такая же, как в простой балке с разницей ординат на – 9,5.
Поперечная сила в неразрезной балке во втором пролете будет такая же, как в простой балке с разницей ординат на – 9,5.
3)Построение эп. Q в третьем пролете:
 Поперечная сила в неразрезной балке в третьем пролете будет такая же, как в простой балке с разницей ординат на +15,3.
Поперечная сила в неразрезной балке в третьем пролете будет такая же, как в простой балке с разницей ординат на +15,3.
Строим эпюру поперечных сил для неразрезной балки. 

7. Построение эпюры изгибающего момента для неразрезной балки. Сначала откладываем на опорах значения опорных моментов, соединяем их линией опорных моментов. Это эпюра опорных моментов.
Эпюру М для неразрезной балки можно построить:
1 вариант – методом «подвешивания». К эпюре опорных моментов «подвешиваем» эпюру M0 по разницам ординат. К примеру, в середине первого пролета на эпюре M0 ордината равна 90, а на эпюре опорных моментов -27. В итоге получим 90-27=63. Это значение и откладываем.
2 вариант – формула для определения изгибающего M в любом сечении неразрезной балки:

Для той же точки первого пролета, которую рассматривали в методе «подвешивания»:
Построение эп. М во 2ом пролете, загруженном равномерно распределенной нагрузкой
Определим положения т. К. по эпюре Q — это точка экстремума.

Определим М неразрезной балки во 2 Теперь нужно определить в этой точке К изгибающий момент М в простой балке:
Теперь нужно определить в этой точке К изгибающий момент М в простой балке:

Таким образом, момент в точке К для неразрезной балки:
Строим эпюру М.
8. Выполним проверку опорных реакций. Покажем реакции  на схеме балки на опорах, направив их вверх. Значения этих реакций определим по скачкам эпюры Q. Таким образом получим:
на схеме балки на опорах, направив их вверх. Значения этих реакций определим по скачкам эпюры Q. Таким образом получим:

Спроецируем все силы, приложенные к балке, и реакции на вертикальную ось, выполним проверку.
Подставим значения, получим 340-340=0
Проверка верна.
Балка на трех опорах — Энциклопедия по машиностроению XXL
Аналогично, горизонтальная балка, лежащая на двух опорах (рис. 66, а), будет статически определимой, так как и здесь две неизвестные реакции и V, входят в два уравнения равновесия (33) плоской системы параллельных сил. Такая же балка на трех опорах (рис. 66, б) будет статически неопределимой. [c.56]| Рис. 134. Равновесие балки на трех опорах. |  |
Балка на трех опорах [c.290]
Балка на трех опорах будет иметь три неизвестные реакции, две из которых определяются из условий- равновесия статики, одна реакция представляет лишнюю неизвестную. За лишнюю неизвестную примем реакцию, возникающую на средней опоре балки. Добавочное условие, которое накладывается на деформацию балки лишней неизвестной, в этом случае заключается в том, что прогиб в сечении над средней опорой равен нулю. Из этого условия мы н будем определять реакцию на средней опоре. После того как эта реакция будет найдена, задача становится статически определимой, [c.290]
В качестве примера рассмотрим.,балку на трех опорах, изгибающуюся равномерно распределенной нагрузкой [c.290]
БАЛКА НА ТРЕХ ОПОРАХ 291 [c.291]
БАЛКА НА ТРЕХ ОПОРАХ 293 [c.293]
В системах, статически неопределимых, замена системы сил статически эквивалентной недопустима даже для определения опорных реакций. Три одинаковые балки на трех опорах, несущие статически [c.18]
Балка на трех опорах (рис. 178, а), несет равномерно распределенную нагрузку интенсивностью д. Определить изгибающий момент на опоре С. [c.173]
Принцип наименьшей работы также можно применять в тех случаях, когда статически неизвестными величинами являются пары сил. Возьмем в качестве примера равномерно нагруженную балку на трех опорах (рис. 290). Если за статически неопределимую величину принять изгибающий момент над средней опорой, то, разрезая балку в В, получаем две свободно лежащие на опорах балки (рис. 290,6), нагруженные неизвестными парами сил кроме известной равномерной нагрузки д. Так как в действительности изогнутая ось балки непрерывна, то никакого поворота конца В балки А В относительно конца В» балки В»С нет. Отсюда [c.291]
Составная балка AD, лежащая на трех опорах, состоит из двух балок, шарнирно соединенных в точке С. На балку действуют вертикально силы, равные [c.347]
Задача 383. Составная балка АО, лежащая на трех опорах, состоит из двух балок АС и СО, шарнирно соединенных в точке С. К балке АС приложены вертикальные силы Р = 8т и Р = т, а к балке СО — пара сил с моментом т—4а т-м, направленным против часовой стрелки. Размеры указаны на рис. а. [c.399]
Пусть теперь та же балка покоится на трех опорах А, В и С (рис. 257, б). Тогда на нее будут действовать, кроме активных сил, три реакции связей N , N( . Но действующие силы образуют по-прежнему плоскую. систему параллельных сил следовательно условий равновесия останется два [c.249]
Таким образом, балка на ,вух опорах является статически определимой, а балка на трех (и более) опорах будет статически неопределимой. [c.249]
Стальная балка лежит на трех опорах, расположенных на одинаковом расстоянии, и несет равномерно распределенную нагрузку интенсивностью 500 Средняя опорная реакция равна 2,5 от. Оба пролета по 4 м. Найти положение по высоте средней опоры. [c.206]
Статически неопределимые системы с изнашивающимися опорами. В механизмах машин, как правило, имеется ряд сопряженных поверхностей, при этом их износ может протекать различным образом. Если износ каждого сопряжения не оказывает влияния на процесс изнашивания других элементов, то их расчет и анализ можно производить независимо, а затем оценивать суммарное воздействие износа сопряжений на выходные параметры механизма. Однако имеется большое число механизмов и сопряжений, износ отдельных поверхностей которых взаимосвязан и не может быть рассмотрен изолированно. Наиболее типичными представителями таких механизмов являются статически неопределимые системы с изнашивающимися опорами (например, вращающийся вал, имеющий три опоры). Реакции, возникающие в опорах, будут определяться с помощью дополнительного уравнения деформаций и с точки зрения сопротивления материалов одинаково как для вращающегося вала, так и для аналогичной балки, лежащей на трех опорах, [c.328]
Этот вывод тождественен тому, который получается при шарнирно опертом по концам стержне. Конечно, существует целый ряд других частот [5], [43]. Для призматической балки, лежащей на трех опорах, при двух одинаковых пролетах получаем, например, три собственных значения (A/)i = 3,14 (Л/)2 = 3,92 (Л )з = 6,28. 94 [c.94]
Рассмотрим балку на трех шарнирных опорах, которая нагружена на одном из концов парой сил с моментом Mq (рис. 14.1а). В задаче необходимо определить реакции, построить эпюры Q и М, изобразить примерный вид изогнутой оси балки. [c.253]
Балка в виде дуги окружности радиуса R устанавливается на трех опорах, расположенных на одном уровне, и нагружается силой Р (см. рисунок). При какой величине радиуса реакции в опорах будут одинаковыми [c.547]
В доказательстве, приводимом ниже, мы будем принимать, что жесткость балки при изгибе постоянна. Рассмотрим часть балки, лежащую на трех опорах. Пусть изгибающие моменты в крайних опорах будут Ж, и М . Если балку рассечь по средней опоре, то она станет статически определимой. В средней опоре имеется изгибающее [c.97]
Сказанное можно пояснить хотя бы таким примером. Требуется определить реакции опор Л, 5 и С неразрезной горизонтальной балки (рис. 78), лежащей на трех опорах. [c.102]
Статическая неопределенность обусловливается излишними связями, накладываемыми на систему материальных точек, и может быть устранена освобождением системы от лишних связей. Такое освобождение системы от лишних связен осуществляется заменой связей силами, величины которых определяются из дополнительных условий, являющихся следствием вводимых физических гипотез. Так, например, рассматривая задачу о равновесии стержня, покоящегося на трех опорах, можно предположить, что одна из опор выполнена нз упругого, легко деформируемого материала. Предположим, что возникающая при деформации сила сопротивления стержня подчинена закону Гука, а ее величина прямо пропорциональна величине сжатия опоры. Предположим, кроме того, что две другие опоры абсолютно жесткие, т. е. их деформации пренебрежимо малы. Обозначив через /о длину несжатой опоры, а через / длину опоры, когда на нее положен груз, силу, действующую со стороны опоры на балку, найдем из условия [c.140]
Составная балка АВ, лежащая на трех опорах, состоит из двух балок, шарнирно соединенных в точке С. На балку дей- [c.40]
Балки, опирающиеся больше чем на две опоры, называются неразрезными или многоопорными балками. Из неразрезных балок мы рассмотрим простейшую, а пмен-но балку на трех опорах. [c.290]
Навье первому пришлось столкнуться с проблемой статической неопределимости, возникаюш ей в расчетах неразрезных балок ). В своей книге Resume des legons… он исследует балку на трех опорах и принимает реакцию одной из них как величину, статически неопределимую. В тех случаях, когда число опор превышает три, выбор реакций как лишних неизвестных величин становится затруднительным, поскольку мы получаем столько же уравнений, сколько имеется промежуточных опор, причем в каждое из таких уравнений входят все лишние неизвестные. Исследование частного случая равных пролетов с равномерно распределенной по всей длине балки нагрузкой или с равными сосредоточенными нагрузками, приложенными по середине каждого из пролетов, показывает, что в этих условиях задача упрош ается и что между реакциями трех последовательных опор суш ествует линейное соотношение. Использование этого соотношения позволяет без особого труда вычислить опорные реакции для любого числа пролетов ). [c.175]
Ло1жерон руля рассчитывается как балка на трех опорах, имеющая нагрузк приходящуюся на руль при его отклонении сосредоточенной силой (С1 ла от тяги управления) [c.468]
В случаё балки на трех опорах (рис. 178, а) имеется один статически неопределимый элемент. Пусть будет этим элементом реакция промежуточной опоры. Тогда при помощи >1етода сложения действия сил решение случая а) можно получить путем сложения [c.172]
На рис. 1.5.2, а изображена балка, лежащая на трех опорах и нагруженная двумя одинаковыми силами в середанах пролетов. Реакции опор будут Дд, Ев, R . Под действием сил балка слегка прогнется, как показано на чертеже. Согласно принципу отвердения равновесие системы не нарушится, если на нее налагаются дополнительные связи. Значит, мы имеем право предположить, чго изогнутая балла стала абсолютно жесткой и составить для нее обычные уравнения статики. Получим [c.26]
Балка швеллерного сечения (профиль № 8), лежащая на трех опорах, сжимается силой Р. Длина одного пролета /i=0,8 м, длина второго пролета h=2lx = =1,6 м. Дано =2-10 кГ1см , Сту=2100 кГ/см . Определить критическую силу Р, пользуясь уравнением трех моментов. [c.210]
Расчет балки, лежащей на трех опорах. На рис. 7.8, а изображена балка, лежащая на трех опорах и нагруженная двумя сосредоточенными силами Р. Устранив среднюю опору и приложив на ее месте неизвестную силу X, получим основную систему (рис. 7.8, б). На рис. 7.8, в показана эпюра изгибающего момента, возникающего под действием сил Р. Ордината средней части эпюры М (Р) равна аР. На рис. 7.8, г изображена эпюра изгибающего момента М (X) от действия силы X. Максимальный момент, появляющийся в сечении, лежащем над устраненной средней опорой, равен ЬХ 2. Если положить / = 1, то получим эпюру М (Р) для единичной внешней нагрузки. Если пpJHЯть X = 1, то получим эпюру М (X) от единичной неизвестной силы, приложенной в сечении, расположенном над средней опорой. В дальнейшем пренебрежем упругим перемещением от сдвигающей силы, малым по сравнению с перемещением от изгиба балки. Согласно выражению (7.15), прогиб в среднем сечении 00 от действия нагрузки Р [c.192]
Стальная двутавровая балка № 18, изогнутая по полуокружности, расположена горизонтально на трех опорах. Конструкция опор позволяет осуществлять защемление и свободное опирание балки. По нижней полке балки передвигается на роликах тележка, несущая платформу для груза. Тележка может быть установлена в любом месте балки и затем нагружена она может также передвигаться и с грузом. Таким образом, могут быть экспериментально определены не только напряжения и перемещения в любом сечении балки, но и их линии влияния. Напряжения измеряют тензометрами для записи линий влияния удобны электротензометры. Прогибы измеряют индикаторами или рейками, углы поворота — инклинометрами, углы закручивания — также инклинометрами, но расположенными перпендикулярно к оси балки. Для измерения больших значений угла закручивания удобнее применять индикаторы, устанавливаемые горизонтально по два в сечении — один вверху, другой внизу — перпендикулярно к оси балки (рис. 188). [c.278]
Тот же прием Навье использует и в расчете балки, заделанной на обеих опорах, а также балки, лежащей на трех опорах. Мы видим, что нахождение кривых прогиба путем интегрирова- [c.96]
Клапейрон в упомянутой выше работе дает уравнение трех моментов в той же самой форме, что и Берто, но не ссылается на работу последнего. Далее, Клапейрон излагает свой метод решения этих уравнений. В заключение он приводит некоторые интересные сведения о трубчатом мосте Британия , представляющем собой неразрезную балку на пяти опорах. Он указывает, что вычисления Молино и Проннье дали нижеследующие значения для наибольших напряжений 1) в середине первого пролета 300 кг1см , 2) на первой опоре 896 кг см , 3) в середине второго пролета 337 кг см , 4) на средней опоре 854 кг см . Отсюда он делает вывод Это величественное сооружение оставляет, таким образом, желать лучшего в отношении целесообразного распределения толщины листов, которые представляются относительно слишком слабыми на опорах . Ниже (см. стр. 194) мы увидим, что при выборе размеров для поперечных сечений этого моста были использованы экспериментальные данные, полученные на свободно опертой модели, а изгибающие моменты на опорах были приравнены моментам в серединах пролетов, что было достигнуто специальным конструктивным приемом. [c.177]
Следовательно, вопрос о деформации балки, лежащей на трех опорах, не может быть решен без учета деформаций балки и опор. В самом деле, мы имеем два условия равновесия балки равенство нулю всех сил и равенство пулю моментов всех сил, а неизвестных реакций, входящих в эти условия, три. Из двух уравнений нельзя определить значения трех неизвестных. Поэтол1у в таких задачах, которые Механики называют задачами со статически неопределимыми реакциями, нельзя иайш реакции опор до решения вопроса о деформации балки или вообще до решения вопроса о деформации тела н его опор, а нужно решать более сложную задачу. Рассмотрим два интересных иримера. [c.325]
При малых значениях и, т. е. когда балка главного направления весьма гибка по равнению с перекрестной балкой, функция фц и) близка к единице и, следовательно, близко к Лщах- балки главного направления будут примерно в таких условиях, как неразрезная балка на трех абсолютно жестких опорах. С возрастанием и функция Фо( ) убывает и обращается в нуль при и = — -л. При этом значении и средняя балка главного направления совер- [c.200]
Это уравнение является развернутым уравнением трех моментов и выражает условие отсутствия угла перелома на п-ой опоре, или условие неразрезности балки на этой опоре. [c.211]
После определения (при помощи уравнений трех моментов) величин всех опорных изгибающих моментов можно определять изгибающие моменты и поперечные силы в пролетах нёразрезной балки и ее опорных реакций. При этом каждый пролет можно рассматривать как простую балку на двух опорах, [c.355]
Заготовку, установленную в центрах и поддерживаемую неподвижным люнетом, можно рассматривать как балку на трех упругих опорах. Эксперименты показали, однако, что жесткость неподвижных люнетов по сравнению с жесткостью задней бабки весьма велика. Упругие отжимы недодаижньтх. люнетов у трех товарных станков 70 [c.70]
Пример 5. Рассмотрим статически неопределимый случай изгиба балки, покоящейся на трех опорах и изгибаемой в двух равных по величине пролетах равномерно распределенной нагрузкой р= onst. Если бы балка опиралась по концам на две опоры А и С (рис. 3.15) и в ее середине В была бы приложена сосредоточенная сила Q, направленная противоположно р, то, согласно равенствам (3.77) и (3.98), прогиб у в точке В под действием Q и р получился бы равным [c.186]
Уравнение трёх моментов — Википедия
Уравнение трёх моментов — уравнение для расчёта моментов в задаче об изгибе неразрезной многопролётной балки[1].
Известно, что балка при наличии дополнительных опор становится статически неопределимой. Одним из методов расчёта таких балок является метод сил. С помощью данного метода выводится уравнение трёх моментов[2]:
- Mi−1li+2Mi(li+li+1)+Mi+1li+1=−6(Ωiaili+Ωi+1bi+1li+1).{\displaystyle M_{i-1}l_{i}+2M_{i}(l_{i}+l_{i+1})+M_{i+1}l_{i+1}=-6\left({\frac {\Omega _{i}a_{i}}{l_{i}}}+{\frac {\Omega _{i+1}b_{i+1}}{l_{i+1}}}\right).}
Здесь Ωi{\displaystyle \Omega _{i}} — площадь эпюры моментов i-й статически определимой балки, ai{\displaystyle a_{i}} — расстояние от центра тяжести i-й эпюры до левого конца балки, bi{\displaystyle b_{i}} — расстояние от центра тяжести i-й эпюры до правого конца балки, li=ai+bi{\displaystyle l_{i}=a_{i}+b_{i}} — длина i-й балки.
Вывод уравнения трёх моментов предусматривает, что после введения шарниров над опорами получается статически определимая система из n{\displaystyle n} балок, каждая из которых представляет простую балку с опорами по концам. Неизвестные в методе сил — моменты, приложенные по концам независимых балок.

Впервые уравнение для расчёта неразрезных балок применил мостостроитель и путейский инженер Берто (Bertot) в 1855 г[3]. Сам же метод применялся ранее (1849) при реконструкции моста через Сену в Аньере (пригород Парижа, ныне известный как Аньер-сюр-Сен, фр. Asnières-sur-Seine), но опубликован Клапейроном в трудах Академии наук только в 1857 г. Так как идея основной системы с неизвестными моментами над опорами впервые была высказана Клапейроном, уравнение трёх моментов связывают с его именем[4]. Дальнейшее развитие теория неразрезных балок получила в работах Отто Мора, который обобщил теорию на случай, когда опоры расположены на разной высоте (1860).
Процедура решения задачи с использованием уравнения трёх моментов такова.
1. Балка режется на отдельные части (простые балки) дополнительными внутренними шарнирами в местах крепления опор.
Обозначения реакций образовавшихся связей: — моменты M0,M1,…,Mn{\displaystyle M_{0},M_{1},…,M_{n}}.
2. Нумеруются пролёты (участки балки между опорами). Число пролётов равно n{\displaystyle n}. Левая консоль считается нулевым пролётом, правая имеет номер n+1{\displaystyle n+1}. Длины пролётов: li{\displaystyle l_{i}}, i=0,…,n+1{\displaystyle i=0,…,n+1}.
3. Из условия равновесия консольных частей определяются моменты M0{\displaystyle M_{0}} и Mn{\displaystyle M_{n}}. Остальные моменты являются неизвестными системы n−1{\displaystyle n-1} уравнений трёх моментов.
4. Строятся эпюры моментов Mp{\displaystyle M_{p}} и перерезывающих сил Qp{\displaystyle Q_{p}} в пролётах и консолях (если они есть) балки от действия внешней нагрузки. Каждый пролёт представляет собой отдельную статически определимую балку.
5. Вычисляются площади эпюр моментов Ωi{\displaystyle \Omega _{i}}, i=1,…,n{\displaystyle i=1,…,n} в пролётах и расстояния от центров тяжести этих площадей до левой (ai{\displaystyle a_{i}}) и правой (bi{\displaystyle b_{i}}) опоры соответствующего пролёта.
6. Решение системы уравнений трёх моментов складывается с эпюрами моментов от внешней нагрузки. Полученная эпюра есть эпюра моментов в неразрезной балке.
Построить эпюру моментов в неразрезной балке длиной 19 метров с четырьмя опорами (рис. 1). На балку действует распределённая нагрузка q1=10{\displaystyle q_{1}=10} кН/м, q2=12{\displaystyle q_{2}=12} кН/м и сосредоточенная сила P=9{\displaystyle P=9} кН.
Рис. 1Длина консоли: l0=4{\displaystyle l_{0}=4} м. Длины пролетов: l1=l2=l3=5{\displaystyle l_{1}=l_{2}=l_{3}=5} м. Получаем основную систему метода сил, вводя шарниры над опорами (рис. 2). Моменты M0{\displaystyle M_{0}} и M3{\displaystyle M_{3}} — величины известные и определяются из условия равновесия консолей. Правой консоли здесь нет, M3=0{\displaystyle M_{3}=0}. Для левой консоли получаем M0=q1l02/2{\displaystyle M_{0}=q_{1}l_{0}^{2}/2}.
Рис. 2Строим эпюры моментов от внешней нагрузки в независимых балках основной (статически определимой) системы (рис. 3). Эпюры строим на сжатом волокне (как принято в машиностроении; в строительстве и архитектуре эпюры моментов принято строить на растянутом волокне).
Рис. 3Записываем уравнения трёх моментов:
l1M0+2M1(l1+l2)+M2l2=−6(Ω1a1/l1+Ω2b2/l2),{\displaystyle l_{1}M_{0}+2M_{1}(l_{1}+l_{2})+M_{2}l_{2}=-6(\Omega _{1}a_{1}/l_{1}+\Omega _{2}b_{2}/l_{2}),}
l2M1+2M2(l2+l3)+M3l3=−6(Ω2a2/l2+Ω3b3/l3).{\displaystyle l_{2}M_{1}+2M_{2}(l_{2}+l_{3})+M_{3}l_{3}=-6(\Omega _{2}a_{2}/l_{2}+\Omega _{3}b_{3}/l_{3}).}
Здесь Ω1=10.8⋅5/2=27,{\displaystyle \Omega _{1}=10.8\cdot 5/2=27,} a1=(2+5)/3=2.333,{\displaystyle a_{1}=(2+5)/3=2.333,} Ω2=Ω3=2fl2/3=125,{\displaystyle \Omega _{2}=\Omega _{3}=2fl_{2}/3=125,} a2=b2=a3=b3=2.5.{\displaystyle a_{2}=b_{2}=a_{3}=b_{3}=2.5.} Решаем систему уравнений M1=7.301{\displaystyle M_{1}=7.301} кНм, M2=−39.325{\displaystyle M_{2}=-39.325} кНм. Строим эпюру от этих моментов (рис. 4).
Рис. 4Складываем (по точкам) эпюры от нагрузки (рис. 3) и от моментов (рис. 4). Получаем эпюру моментов в балке (рис. 5).
Рис. 5Очевидным достоинством метода является простота матрицы системы линейных уравнения задачи. Эта матрица — трёхдиагональная, что позволяет применять различные упрощённые численные схемы решения.
- ↑ Кирсанов М. Н. . Maple и Maplet. Решения задач механики. — СПб.: Лань, 2012. — 512 с. — ISBN 978-5-8114-1271-6. — С. 179—181.
- ↑ Феодосьев В. И. . Сопротивление материалов. — М.: Государственное издательство физико-математической литературы, 1960. — 536 с. — С. 217.
- ↑ Бернштейн С.А. Очерки по истории строительной механики. — М.: Государственное издательство литературы по строительству и архитектуре, 1957. — 236 с. — С. 209.
- ↑ Тимошенко С. П. . История науки о сопротивлении материалов. 2-е изд. — М.: URSS, 2006. — 536 с. — ISBN 5-484-00449-7. — С. 176.
- Киселёв В. А. . Строительная механика. Общий курс. — М.: Стройиздат, 1986. — 520 с.
- Горшков А. Г., Трошин В. Н., Шалашилин В. И. . Сопротивление материалов. — М.: ФИЗМАТЛИТ, 2002. — 544 с. — ISBN 5-9221-0181-1.
Статически неопределимые балки. Уравнения трех моментов
1. Двухпролетная балка
Рисунок 315.1. Приведение двухпролетной балки к основной и вспомогательной системам при методе моментов.
1. Когда мы рассекаем балку на промежуточной статически неопределимой опоре (рис. 315.1.б)), мы получаем две статически определимых балки с общей опорой В (рис.315.1.в)). Рассчитать такие балки — не проблема, а для удобства расчетов даже созданы соответствующие таблицы, пример такой таблицы можно посмотреть здесь. Балки, показанные на рисунке 315.1.в), являются элементами основной системы. Балки, показанные на рисунке 315.1.г), являются элементами вспомогательной системы.
2. Под действием приложенной нагрузки поперечные сечения балок не будут находиться в плоскости, перпендикулярной к основной оси (оси х), а будут иметь некоторый наклон. Другими словами, между плоскостью, перпендикулярной к основной оси, и поперечным сечением будет некоторый угол, называемый углом поворота поперечного сечения Θ. На рисунке 315.1.е) показаны углы поворота для крайнего правого сечения левой балки и крайнего левого сечения правой балки. Таким образом между указанными поперечными сечениями образуется угол наклона φ. Общая эпюра углов поворотов поперечных сечений для статически определимых балок основной системы будет выглядеть приблизительно так, как показано на рисунке 315.1.д).
3. Между тем балка-то у нас неразрезная, а это означает, что угол между двумя очень близкими относительно оси х сечениями будет стремиться к нулю, а так как мы рассекаем балку мысленно, то крайнее правое сечение левой балки и крайнее левое сечение правой балки — это одно и то же поперечное сечение неразрезной балки и для такого сечения угол наклона φ = 0.
4. Если к рассматриваемым поперечным сечениям балок приложить изгибающие моменты (рис. 315.1.г), то при определенном значении моментов суммарный угол наклона поперечных сечений будет равен углу наклона между поперечными сечениями балок основной системы, только значение это будет иметь обратный знак (рис.315.1.ж).
5. Таким образом, если сложить угол наклона смежных поперечных сечений балок основной системы и угол наклона смежных поперечных сечений балок вспомогательной системы, то угол наклона φ на общей эпюре углов поворотов будет равен нулю (рис.315.1.и)), при этом угол поворота поперечного сечения Θ неразрезной балки может быть не равен нулю.
6. Так как в действительности никакие внешние моменты на статически неопределимых опорах не прикладываются, а мы всего лишь заменяем внутренние напряжения внешними моментами, то на суммарной эпюре моментов (на рисунке 315 не показана) на статически неопределимых опорах не может быть скачков (могут быть только точки экстремума). Из этого следует, что значение момента, приложенного к крайнему правому сечению, должно быть равно значению момента, приложенного к крайнему левому сечению:
Мл = Мп = М (315.1.1)
Примечание: Самое трудное при работе с моментами и углами поворота — уследить за знаками. Сейчас считается, что если сила или момент приводят к растяжению нижней части сечения, то эпюра моментов рисуется снизу, но такой момент считается положительным, соответственно, если сила или момент приводят к растяжению верхней области сечения, то эпюра моментов рисуется сверху, но такой момент считается отрицательным. Дело в том, что вне зависимости от того, сверху или снизу рисуется эпюра моментов в поперечных сечениях рассматриваемых конструкций возникают нормальные напряжения и если рассматривать только нижнюю часть сечения, то положительный момент означает растяжение в нижней части и таким образом знак «+» символизирует увеличение длины в нижней части рассматриваемой конструкции, а отрицательный момент означает сжатие в нижней части сечения и знак»-» символизирует уменьшение длины конструкции в нижней части. Из этого следует, что если момент для рассматриваемого сечения (точки на оси х) направлен по часовой стрелке, то такой момент положительный, а если против часовой стрелки, то момент отрицательный. Таким образом знак момента зависит от точки (поперечного сечения), относительно которой данный момент рассматривается. Так для смежных статически определимых балок моменты, показанные на рисунке 315.1.г), будут отрицательными, а для поперечного сечения на опоре В неразрезной балки моменты будут иметь различный знак и в сумме дадут ноль. Приблизительно то же самое можно сказать и о углах поворота поперечных сечений. Если сечение наклонено вправо от оси у, то такой угол поворота можно считать отрицательным, если влево от оси у, то такой угол поворота будет считаться положительным, что и отражено на соответствующих эпюрах углов поворотов на рисунке 315.1. Между тем при определении прогиба знак угла поворота крайних сечений будет зависеть от направления интегрирования и от того, прогиб вверх или вниз будет считаться положительным. Так, если начальный угол поворота (угол поворота на одной из опор) будет приводить к растяжению в нижней области, то такой угол поворота может считаться положительным, например, для рассматриваемых нами статически определимых балок основной системы значения углов поворота на обеих опорах могут рассматриваться, как положительные. При действии положительного изгибающего момента углы поворота на опорах также будут положительными.
7. Если к одной из опор статически определимой балки, например опоре В, приложить положительный изгибающий момент, то в это приведет к изменению угла поворота поперечного сечения на опоре В на угол θB= Мl/3EI и к изменению угла поворота на опоре А на угол θА = Ml/6EI. На рисунке 315.1 для наглядности суммарного взаимодействия показаны отрицательные изгибающие моменты, которые приводят к отрицательным значениям углов поворота, но чтобы не путаться со знаками, изначально значения углов поворота для основной и для вспомогательной систем принимаются положительными.
Например, для двухпролетной балки, показанной на рисунке 315.1, угол наклона между поперечными сечениями балок основной системы будет составлять:
φВ = qa3/24EI +qb3/24EI = q(a3 + b3)/24EI (315.1.2)
значение угла наклона на смежной опоре при приложении моментов к балкам вспомогательной системы
φВ = МВпa/3EI + MВлb/3EI = M(a + b)/3EI = Ml/3EI (315.1.3)
φВ = φВ + φВ = q(a3 + b3)/24EI + Ml/3EI = 0 (315.1.4)
M = — q(a3 + b3)/8l (315.1.5)
после этого с учетом опорного момента определяются опорные реакции
A = A + A = qa/2 + M/a = qa/2 — q(a3 + b3)/8la (315.1.6)
C = C + C = qb/2 + M/b = qb/2 — q(a3 + b3)/8lb (315.1.7)
B = Bп + Вл + Вп + Вл = qa/2 + q(a3 + b3)/8la + qb/2 + q(a3 + b3)/8lb (315.1.8)
После того, как расчетные реакции определены, дальнейший расчет выполняется, как для обычной статически определимой балки, вот только необходимо выполнить дополнительные проверки, так прогиб на всех опорах при действующих нагрузках должен быть равен нулю.
При равных пролетах, т.е. при а = b = l/2
φВ = ql3/192EI + ql3/192EI = ql3/96EI = qa3/12 (315.1.9)
φВ = ql3/96EI + Ml/3EI = qa3/12EI + 2Mа/3EI = 0 (315.1.10)
M = — ql2/32 = — qa2/8 (315.1.11)
Опорные реакции составят
A = C = qa/2 — qa/8 = 3qа/8 (315.1.12)
B = 2(qa/2 + qa/8) = 10qa/8 (315.1.13)
Если однопролетная балка имеет одну жестко защемленную опору и шарнирную опору, то такую балку можно рассматривать как двухпролетную неразрезную шарнирно опертую балку, у которой один из пролетов равен нулю и соответственно момент на жестко защемленной опоре будет М = — ql2/8, согласно формулы (315.1.5). Это позволяет рассчитывать данным методом не только шарнирно опертые многопролетные балки, но и балки, имеющие жесткое защемление на концах.
2. Трехпролетная балка
При рассмотрении трехпролетной балки у нас появится еще одна неизвестная величина — момент на опоре С:
Рисунок 315.2. Приведение трехпролетной балки к основной и вспомогательным системам
То есть угол наклона между смежными сечениями на опоре В балок вспомогательной системы будет зависеть не только от значения моментов, приложенных на рассматриваемой опоре, но также и от значения момента, приложенного на опоре С. И тогда формула для определения угла наклона на опоре В будет выглядеть так:
φВ = МВпa/3EI + MВлb/3EI — МСпb/6EI = MB(a + b)/3EI + MCb/6EI (315.2.2)
φВ = q(a3 + b3)/24EI + MB(a + b)/3EI + MCb/6EI = 0 (315.2.3)
Соответственно для опоры С:
φС = MС(b + c)/3EI — MВb/6EI (315.2.4)
φС = q(b3 + c3)/24EI + MC(b + c)/3EI + MBb/6EI = 0 (315.2.5)
Решая систему из двух уравнений (315.4.3) и (315.4.4), можно найти значения моментов на опорах. Например при равных пролетах a = b = c решение задачи значительно упрощается, так как и моменты МВ и МС, действующие на опорах, при этом будут равными из-за симметричности балки и равномерно распределенной нагрузки:
φВ = φС= qa3/12EI + 2Ma/3EI + Ma/6EI = 0 (315.2.6)
5Ma/6EI = — qa3/12EI (315.2.7)
M = — qa2/10 (315.2.8)
Когда мы решали подобную задачу методом сил, то получили следующие уравнения:
Δ10 + Δ1У1 + Δ1У2 = 0 (314.4.2)
Δ20 + Δ2У1 + Δ2У2 = 0
Если мы угол наклона заменим греческой буквой Δ, а статически неопределимые опоры пронумеруем, то уравнения (315.2.3) и (315.2.5) примут вид:
Δ10 + Δ11 + Δ12 = 0 (314.4.2)
Δ20 + Δ21 + Δ22 = 0
т.е. мало чем будут отличаться от канонических уравнений метода сил.
Если у балки будет 4 пролета, то в итоге мы получим систему из 3 уравнений, в одном из которых будет 3 неизвестных члена, а в первом и последнем — по 2 неизвестных члена. Соответственно для расчетов 5 пролетной балки придется составить систему из 4 уравнений, в двух из которых будет по 3 неизвестных члена, а в первом и последнем также по 2 неизвестных члена, для 6 пролетной — из 5 уравнений и так далее, но при этом количество неизвестных членов в первом и последнем уравнении всегда будет равно двум, а в остальных уравнениях — трем, так как количество моментов, действующих на опорах смежных балок вспомогательных систем, не может быть больше 4. А так как моменты, действующие на рассматриваемой опоре, равны согласно (315.1.1), то количество неизвестных в уравнениях сокращается до 3 и потому уравнения вида (315.2.3) и (315.2.5) называются уравнениями трех моментов.
Для любой многопролетной балки уравнение трех моментов для n-ной опоры можно записать так:
Mn-1ln/6EI + Mn(ln + ln+1)/3EI + Mn+1ln+1/6EI = — φn (315.3.1)
А если обе части уравнения умножить на 6EI, то уравнение трех моментов будет выглядеть так:
Mn-1ln + 2Mn(ln + ln+1) + Mn+1ln+1 = — 6φnEI (315.3.2)
где φn — рассмотренный нами суммарный угол наклона между смежными сечениями на n-ной опоре.
Произведение φnEI иногда для упрощения записи рассматривается, как суммарная фиктивная опора Rnф:
φnEI = Rnф = Вnф + An+1ф = ωnan/ln + ωn+1bn+1/ln+1 (315.3.3)
Физический смысл этой формулы следующий: с точки зрения строительной физики сила, момент, угол поворота и прогиб — это не какие-то случайные понятия, а четко связанные между собой. Например, когда мы определяем опорную реакцию В при действии равномерно изменяющейся нагрузки (от 0 на опоре А до q на опоре В), мы умножаем площадь нагрузки (ql/2) на расстояние от опоры А до центра тяжести этой площади (2/3l) и затем делим это все на длину пролета (l), в итоге В = ql/3, соответственно А = ql/6. А если в качестве грузовой эпюры рассматривать эпюру моментов, также имеющую вид треугольника (например, при моменте, приложенном на опоре В), то значение фиктивных реакций составит Вф = Мl/3, Аф = Ml/6. В общем случае эту закономерность можно отобразить так:
Рисунок 315.3. Определение суммарной фиктивной реакции по эпюрам моментов для балок основной системы.
Однако в большинстве случаев чертить эпюры моментов для балок основной системы, затем определять центры тяжести этих эпюр и расстояния до центров тяжести нет большой необходимости, так как для наиболее распространенных вариантов приложения нагрузки фиктивные опорные реакции давно известны и определить их можно по соответствующим таблицам. Пример такой таблицы представлен ниже.
Таблица 315.1. Фиктивные опорные реакции для различных вариантов загружения балки основной системы
4. Решение системы уравнений
После того, как углы поворота на опорах (фиктивные опорные реакции) для всех балок основной системы определены, можно приступать к решению системы уравнений. Вот только, если пролетов у балки много, то запись окончательного уравнения, позволяющего определить один из неизвестных моментов, может занять не одну минуту и не одну страницу. В таких случаях можно воспользоваться следующей методикой:
Для балки, имеющей k пролетов, потребуется составить k — 1 уравнений. Если значения выражений — 6Rnф заменить параметром ci, то уравнения будут иметь следующий вид:
(315.4.1)
Если умножить все уравнения на пока произвольные параметры αi, а затем сложить все левые и правые части уравнений системы (315.4.1), то итоговое уравнение после соответствующих преобразований, позволяющих сократить запись, будет иметь вид:
(315.4.2)
Теоретически множители α могут иметь такие значения, при которых все выражения в квадратных скобках (множители для Мn в формуле (315.4.2)), кроме последнего, будут равны нулю. На основании этого предположения из уравнения (315.4.2) можно составить еще одну дополнительную систему уравнений:
(315.4.3)
Количество уравнений в такой системе будет k — 2, с k — 1 неизвестными параметрами α. Так как число параметров α на единицу больше количества уравнений, то для решения системы значение одного из этих параметров задается произвольно. Наиболее удобным для дальнейших расчетов будет принять значение α1 = 1. Тогда значения остальных коэффициентов α можно определить, решая систему уравнений (315.4.3):
(315.4.4.1)
В общем виде:
(315.4.5)
Примечание: Если придать абстрактным математическим коэффициентам α конкретный физический смысл, то коэффициенты αn есть не что иное, как такое соотношение моментов на соседних опорах , при котором суммарный угол наклона на рассматриваемой опоре будет равен нулю и тогда эти коэффициенты можно выразить так αn = Mn/Mn-1. Например, если первое уравнение системы (315.4.1) разделить на М1, то это уравнение c учетом вышесказанного можно записать так:
(315.4.6)
тогда
(315.4.4.2)
После подставления определенных вышеуказанным способом параметров α уравнение (315.4.2) примет вид
(315.4.7)
Соответственно значение Мk-1 будет составлять
(315.4.8)
После этого полученное значение Мk-1 подставляется в последнее уравнение системы (315.4.1) и определяется значение Мk-2. Из предпоследнего уравнения после подставления значений Мk-1 и Мk-2 определяется значение Мk-3 и т.д. Таким образом количество неизвестных в уравнениях системы (315.4.1) сводится к одному.
Если на одном или обоих концах балки есть нагруженные консоли, то определить изгибающие моменты на крайних опорах — не проблема. Значения этих моментов подставляются в уравнение трех моментов, как известные величины, тогда в первом и последнем уравнениях также будет по 3 члена. Если один или оба конца рассчитываемой балки защемлены, то жесткое защемление рассматривается как дополнительный пролет с длиной l = 0, таким образом придется составить еще одно или два уравнения.
5. Уравнение трех моментов для балки с переменной жесткостью:
Когда мы умножали обе части уравнения (315.3.1) на 6EI, то тем самым задавали момент инерции I, как некую постоянную величину. Между тем момент инерции также может быть переменной величиной (например, когда многопролетная железобетонная плита имеет различное армирование в пролетах) и для таких случаев уравнение моментов можно записать так:
(315.5.1)
где
(315.5.2)
Io — момент инерции одного из участков балки, принятый за основу.
Вот, в принципе и все теоретические предпосылки для расчета статически неопределимых конструкций методом моментов. А как эту теорию можно применить на практике, рассказывается отдельно.
3. Особенности расчета статически неопределимых многоопорных балок.
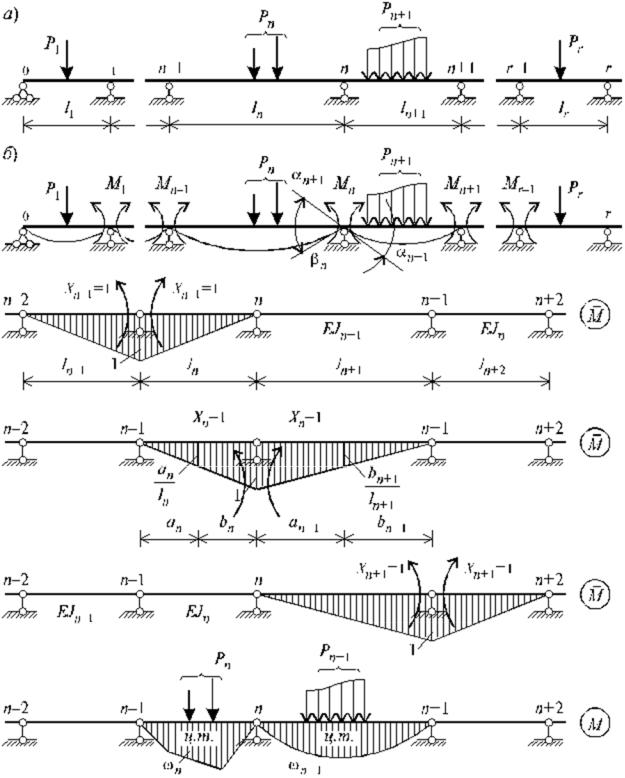
Неразрезной балкой называется статически неопределимая балка, опирающаяся в пролете на конечное число шарнирных опор. Крайние сечения неразрезной балки могут быть свободны, заделаны или шарнирно оперты. Одна из опор неразрезной балки имеет связь, препятствующую смещению балки вдоль ее оси.
Расчет неразрезной балки (рис. 24, а) можно выполнить, как и любой статически неопределимой системы методом сил. Основную систему для расчета неразрезной балки получим, удалив из нее связи, препятствующие взаимному повороту смежных сечений балки над ее опорами, т.е. поместив шарниры в опорных сечениях балки (рис. 24, б).

Рис. 24
Неизвестными являются изгибающие моменты, возникающие в сечении неразрезной балки над опорами.
Выделим из основной системы четыре примыкающих друг к другу пролета со средней опорой номером n и построим единичные и грузовые эпюры (рис. 25). Из анализа единичных эпюр видно, что в любом каноническом уравнении только три единичных коэффициента будут отличны от нуля. Напишем одно из канонических уравнений в общем виде:
Подсчитаем единичные и грузовые коэффициенты, применяя правило Верещагина «перемножения» эпюр:
(14.23)
Подставим найденные коэффициенты в (14.22), получим:
|
|
|
| (14.24) |
|
В случае | балки | постоянного | сечения J1 = J2 =…= Jn = Jn+1 и | введя | |
обозначения Xn 1 | = M n 1; Xn = Mn; Xn+1 = Mn+1, получим: |
|
| ||
|
|
| . | (14.25) |
|
Это и есть уравнение | трех моментов для неразрезной | балки постоянного | |||
сечения. В этом уравнении неизвестными являются изгибающие моменты на опорах. Если у неразрезной балки все опоры шарнирные, то таких уравнений можно составить столько, сколько у балки промежуточных опор.
При наличии на концах балки нагруженных консолей, изгибающие моменты на крайних опорах войдут в уравнение трех моментов, как известные величины, а при отсутствии консолей эти моменты будут равны 0.
Если конец неразрезной балки защемлен, то для применения уравнения (14.25)
необходимо, отбросив заделку, ввести с ее стороны дополнительный пролет 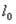 =0 (рис.25). Такая система будет деформироваться также, как балка с жесткой заделкой.
=0 (рис.25). Такая система будет деформироваться также, как балка с жесткой заделкой.
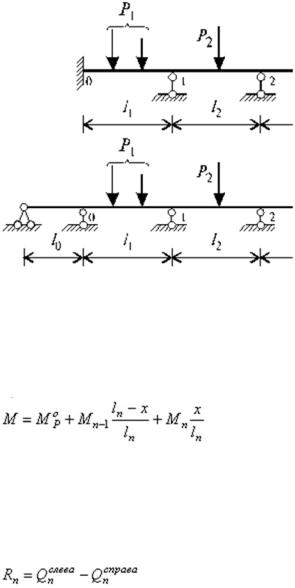
Рис. 25
Решая совместно, составленные таким образом уравнения, найдем все неизвестные изгибающие моменты на опорах. Далее для построения эпюр M и Q, каждый пролет неразрезной балки рассматриваем как балку на двух шарнирных опорах, загруженных внешней нагрузкой и двумя опорными моментами. Ординаты эпюр могут быть подсчитаны по формулам:
где 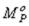 и
и 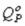 ординаты эпюр М и Q от внешней нагрузки в основной системе.
ординаты эпюр М и Q от внешней нагрузки в основной системе.
Чтобы убедиться в правильности построения эпюр М и Q необходимо провести
проверку равновесия неразрезной балки по уравнениям: 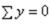 ;
; 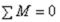 .
.
Для этого следует определить вертикальные опорные реакции неразрезной балки, используя эпюру Q:
Задача равновесия балки на трех опорах
Подвижную опору заменяем вертикальной реакцией Яя, а неподвижную опору С — горизонтальной Хс и вертикальной Y (рис. 39, б). Имеется три неизвестных — задача [c.57]Балка на трех опорах будет иметь три неизвестные реакции, две из которых определяются из условий- равновесия статики, одна реакция представляет лишнюю неизвестную. За лишнюю неизвестную примем реакцию, возникающую на средней опоре балки. Добавочное условие, которое накладывается на деформацию балки лишней неизвестной, в этом случае заключается в том, что прогиб в сечении над средней опорой равен нулю. Из этого условия мы н будем определять реакцию на средней опоре. После того как эта реакция будет найдена, задача становится статически определимой, [c.290]
Из примеров, рассмотренных в 25 и 26, мы видим, что в общем случав при равновесии плоской системы сил, приложенных к данному твердому телу, мы имеем три уравнения в том же случае, если к данному телу приложена уравновешивающаяся система параллельных сил, мы располагаем только двумя уравнениями. Отсюда следует, что в первом случае задача является статически определенной, если число неизвестных сил не превышает трех во втором же случае число неизвестных сил не должно быть больше двух. В противном случае задача становится статически неопределенной, так как число уравнений окажется меньше числа неизвестных. Так, например, задача определения опорных реакций в случае балки, нагруженной перпендикулярными к ней силами и лежащей па трех опорах, является статически неопределенной, так как неизвестных реакций будем иметь в этом случае три, а уравнений только два. Точно так же, если бы ферма, рассмотренная в примере 33 ( 25), имела два неподвижных опорных шарнира и D, то задача оказалась бы статически неопределенной, так как мы имели бы в этом случае четыре неизвестные реакции (по две в каждом шарнире), а уравнений только три. [c.118]
Рассмотрим, например, балку, изображенную на рис. УИ.25, а. Число неизвестных опорных реакций равно четырем три реакции заделки и одна реакция подвижной опоры. Уравнений статики — три. Таким образом, лишних неизвестных— одно. Балка одни раз статически неопределима. Лишние неизвестные в задачах такого типа являются результатом наличия связей, лишних для равновесия абсолютно твердого тела. [c.172]
Два условия статики (условия равновесия всей балки) и три условия (12.32) дадут возможность определить пять неизвестных Лв, Лс. Vo и бо- В том случае, когда имеется п шарнирных опор, в число неизвестных войдут п реакций опор и два начальных параметра 0о и v , тогда как Мо = 0. Для определения этих п + 2 неизвестных можно составить п + 2 уравнения два уравнения статики и п условий равенства нулю перемещений балки над опорами. Таким обрааэм, задача ставится разрешимой. Для задачи с тремя опорами (рис. 12.22) из условий статики [c.261]
Эта задача может быть решена и другим путем. Можно рассмотреть равновесие балки D и равновесие всей двухпролетной балки AB D. Из уравнений равновесия для балки D (4), (5) и (6) легко находятся реакции шарнира С и опоры D, так как эти три уравнения содержат три неизвестных R x, D- Рассматривая далее равновесие двухпролетной балки AB D, составим три уравнения равновесия, из которых определяются три оставшихся неизвестных R x, лу> в- [c.84]
Следовательно, вопрос о деформации балки, лежащей на трех опорах, не может быть решен без учета деформаций балки и опор. В самом деле, мы имеем два условия равновесия балки равенство нулю всех сил и равенство пулю моментов всех сил, а неизвестных реакций, входящих в эти условия, три. Из двух уравнений нельзя определить значения трех неизвестных. Поэтол1у в таких задачах, которые Механики называют задачами со статически неопределимыми реакциями, нельзя иайш реакции опор до решения вопроса о деформации балки или вообще до решения вопроса о деформации тела н его опор, а нужно решать более сложную задачу. Рассмотрим два интересных иримера. [c.325]
Решение. Применим метод сечений — разрежем тяги и приложим в местах разрезов продольные силы и (рис. 240). Помимо этих сил и активной силы Р, на балку действует вертикально направленная реакцияУ шарнирно-неподвижной опоры. Вообще, как известно из статики, реакция шарнирно-неподвижной опоры дает две составляющих, но в данном случае к балке никаких горизонтально направленных сил не приложено и потому, очевидно, горизонтальная составляющая реакции равна нулю. Таким образом, на балку действует система параллельных сил, расположенных в одной плоскости. Для такой системы сил статика дает два независимых уравнения равновесия, а неизвестных сил три У , и Л , следовательно, задача статически неопределима. Составим уравнения равновесия [c.235]
Рассмотрим, например, равновесие горнзоптальной балки, i которой приложены заданные силы и Р,,,. Левая опора бал] и — неподвижный шарнир А, а правая — подвил 1ый краток Л (рис. 3.9). Требуется определить реакции опор. Мы пл еем три неизвестные составляющие реакций (см. п. 2.9 гл. I) Хд, F,-, Л в, и в нашем распоряжении три уравиеиия равновесия. Следовательно, задача статически определенная. [c.68]
2.3. Балки и опоры. Реакции и их вычисление
Балками будем называть прямолинейные стержни, работающие на изгиб. В сопротивлении материалов термин «балка» значительно шире, чем в обычном употреблении этого слова: с точки зрения расчета на прочность, жесткость и устойчивость балкой является не только строительная балка, но также и вал, болт, ось железнодорожного вагона, зуб шестерни и т. д.
Вначале ограничимся построением эпюр для простейшего случая изгиба балок, при котором все заданные нагрузки лежат в одной плоскости, называемой силовой (на рис. 4, а — плоскость П), причем эта плоскость совпадает с одной из главных плоскостей балки. Такой случай будем называть плоским изгибом.
На расчетной схеме балку принято заменять ее осью (рис. 4, б). При этом все нагрузки, естественно, должны
Рис 4 быть приведены к оси балки и силовая плоскость будет совпадать с плоскостью чертежа.
Как правило, балки имеют опорные устройства — опоры. Для расчета же их схематизируют в виде трех основных типов опор:
а) шарнирно-подвижная
опора (рис.
5, а), в которой может возникать только
одна составляющая реакции — 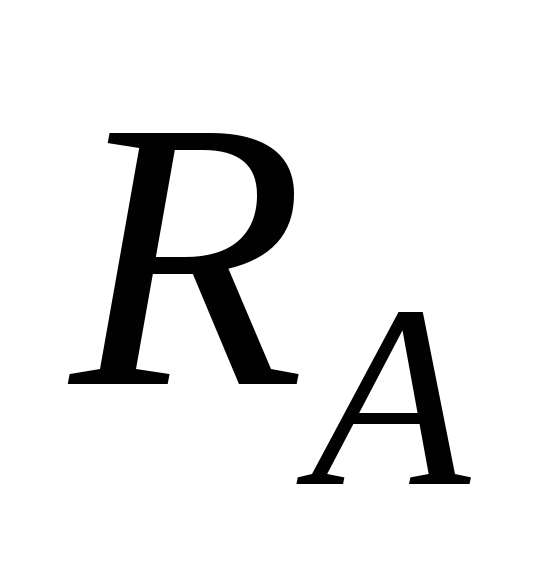 , направленная
вдоль опорного стерженька;
, направленная
вдоль опорного стерженька;
б) шарнирно-неподвижная
опора (рис.
5, б), в которой могут возникать две
составляющие — вертикальная реакция 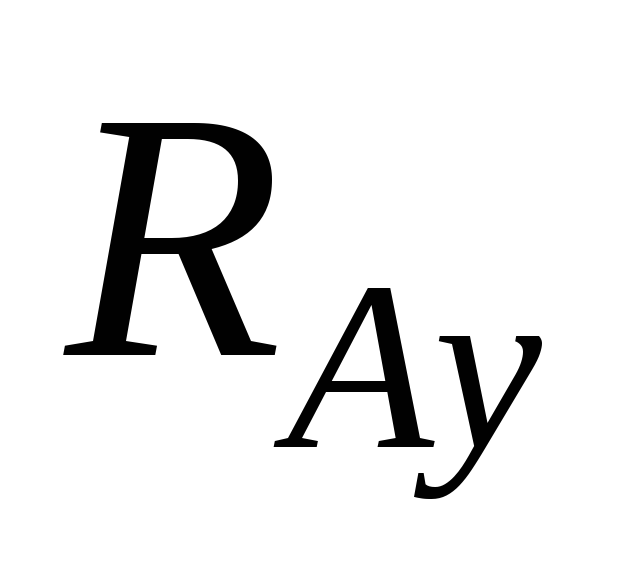 и горизонтальная
реакция
и горизонтальная
реакция 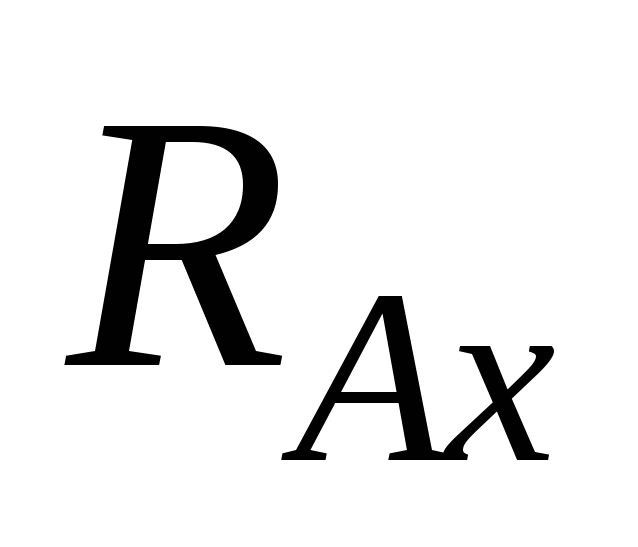
в) защемление (иначе жесткое
защемление или заделка), где
могут быть три составляющие — вертикальная  и
горизонтальная
и
горизонтальная 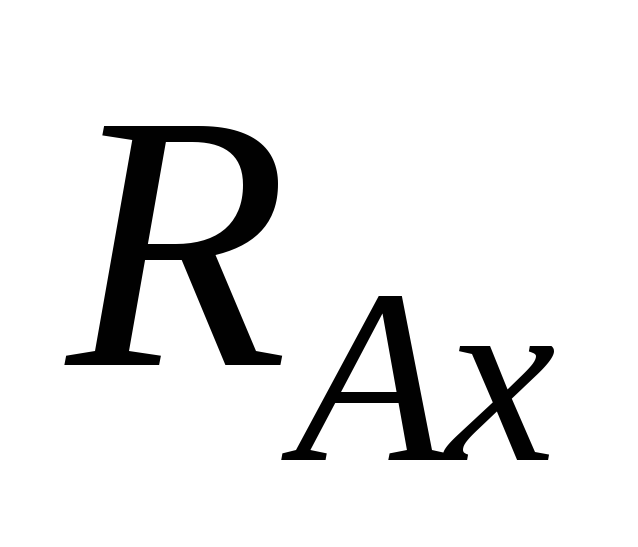 реакции
и опорный момент Ма (рис.
5, в).
реакции
и опорный момент Ма (рис.
5, в).
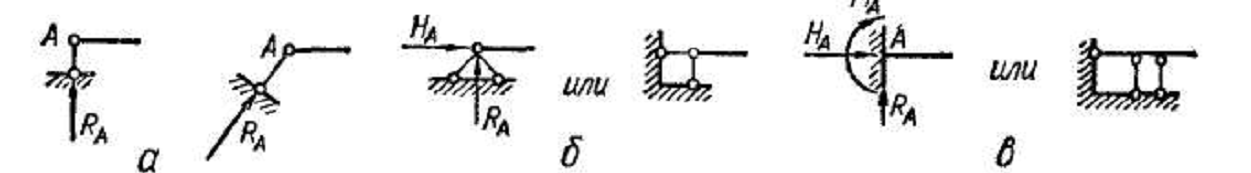
Рис 5
Все реакции и моменты считаются приложенными в точке А — центре тяжести опорного сечения.
Балка, показанная на рис. 6, с, называется простой, или однопролетной , или двухопорной, а расстояние l между опорами — пролетом.
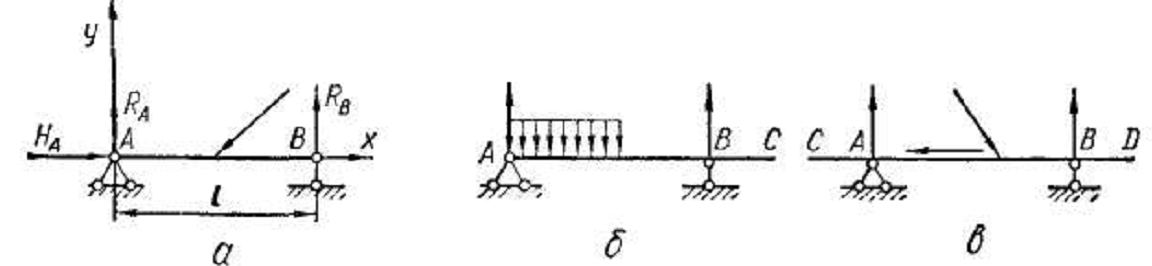
Рис 6
Консолью называется балка, защемленная одним концом и не имеющая других опор (рис. 4, б), или часть балки, свешивающаяся за опоры (часть ВС на рис. 6, б; части АС и BD на рис. 6, е). Банки, имеющие свешивающиеся части, называют консольными (рис. 6, б, в).
Для плоской системы сил можно составить три уравнения статики для определения неизвестных реакций.
Поэтому балка будет статически определимой, если число неизвестных опорных реакций не превышает трех; в противном случае балка статически неопределима. Очевидно, что балки, изображенные на рис. 4 и 6, статически определимы.
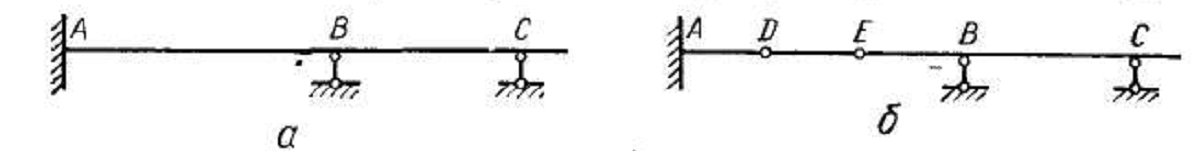
Рис 7
Балка, изображенная на рис. 7, а, называется неразрезной и является статически неопределимой, поскольку имеет пять неизвестных опорных реакций: три в опоре А и по одной в опорах В и С.
Поставив в сечениях балки шарниры, например в точках D и Е (рис. 7, б), получим статически определимую шарнирную балку, ибо каждый такой промежуточный шарнир к трем основным уравнениям статики прибавляет одно дополнительное уравнение: сумма моментов относительно центра шарнира от всех сил, расположенных по одну сторону от него, равна нулю.
Построение эпюр для статически неопределимых балок требует умения вычислять деформации, а поэтому ограничимся пока исключительно статически определимыми балками.
Способы определения опорных реакций изучают в курсе теоретической механики. Поэтому здесь остановимся только на некоторых практических вопросах. Для этого рассмотрим простую балку (рис. 6, а).
1. Опоры обычно обозначают буквами А и В. Три неизвестные реакции находят из следующих уравнений равновесия:
а)
сумма проекций всех сил на ось балки
равна нулю: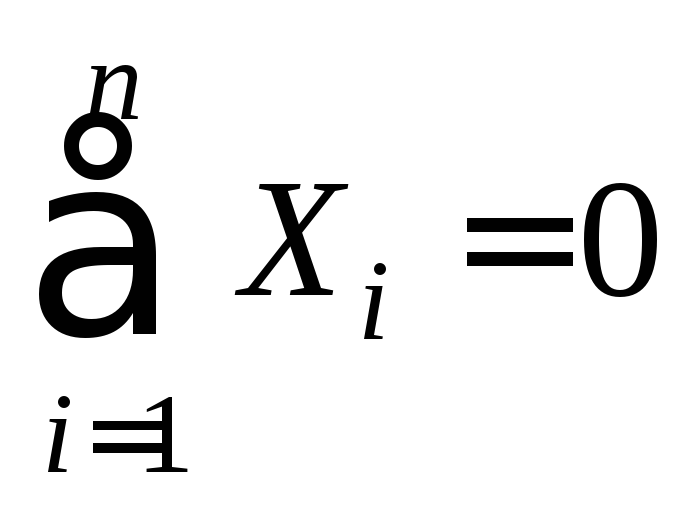 откуда находят
откуда находят 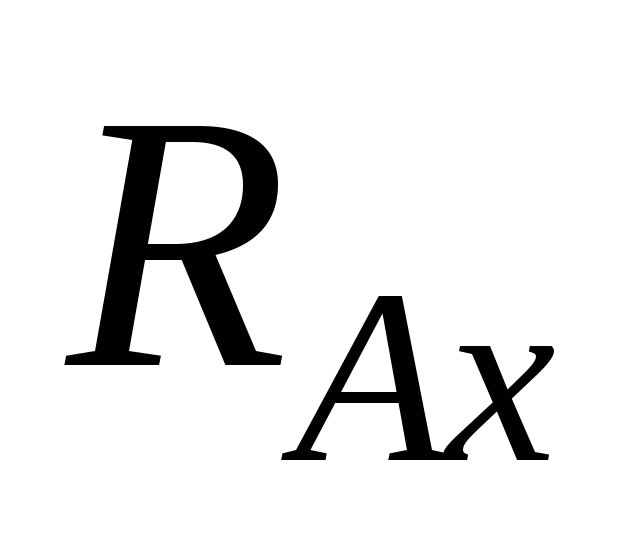
б)
сумма моментов всех сил относительно
опорного шарнира А равна
нулю: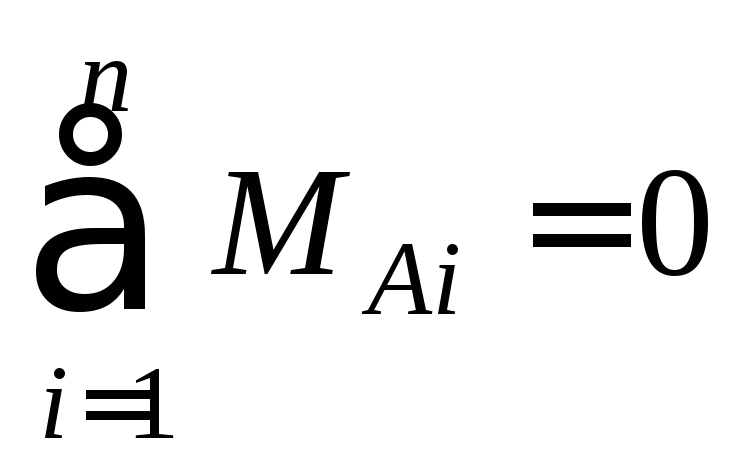 откуда находят
откуда находят 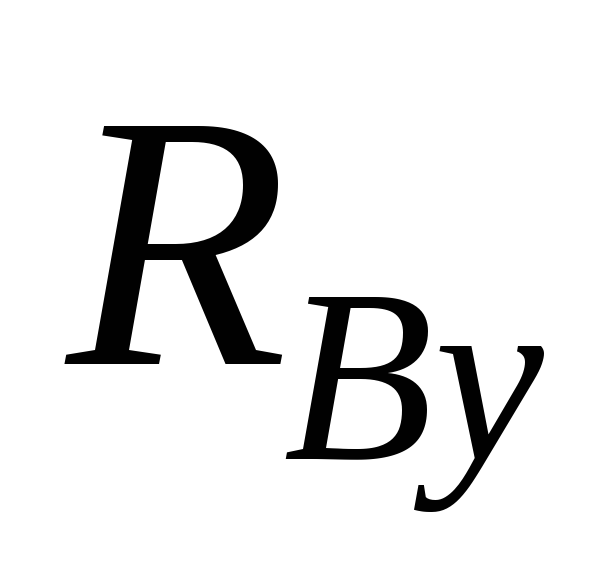 .
.
в)
сумма моментов всех сил относительно
опорного шарнира В равна
нулю: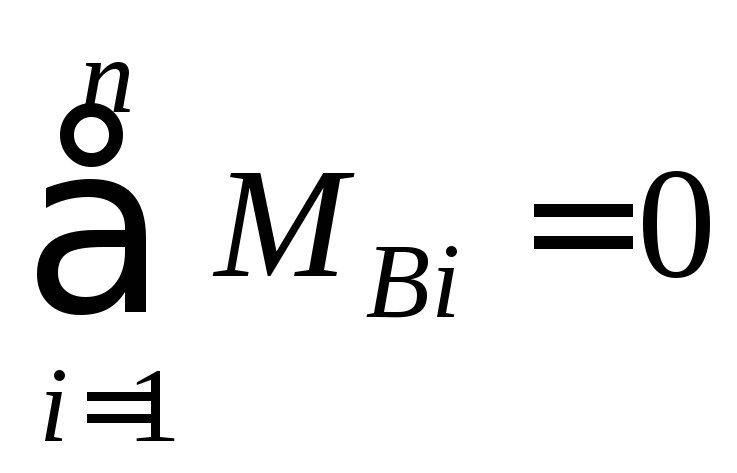
откуда
находят 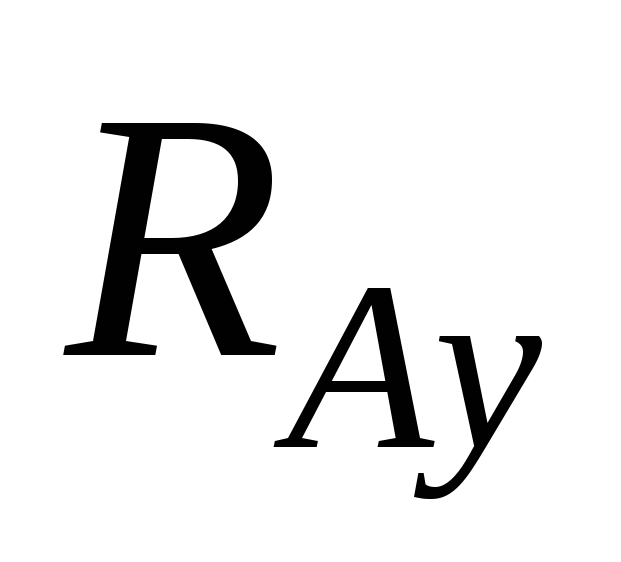 .
.
2. Для контроля можно использовать или условие равенства нулю суммы проекций на вертикаль:
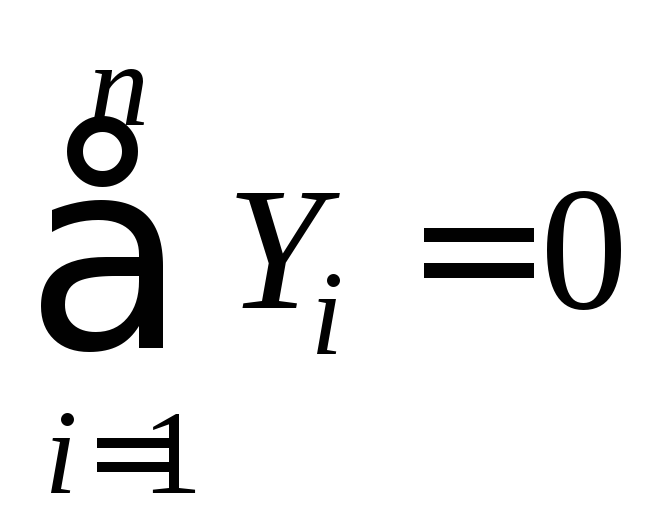
или условие равенства нулю суммы моментов относительно какой-либо точки С, отличной от А и В, т. е.
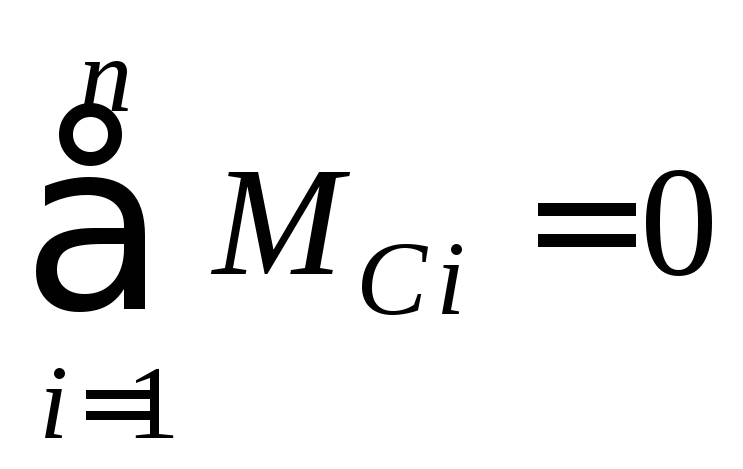 У
У
Условием 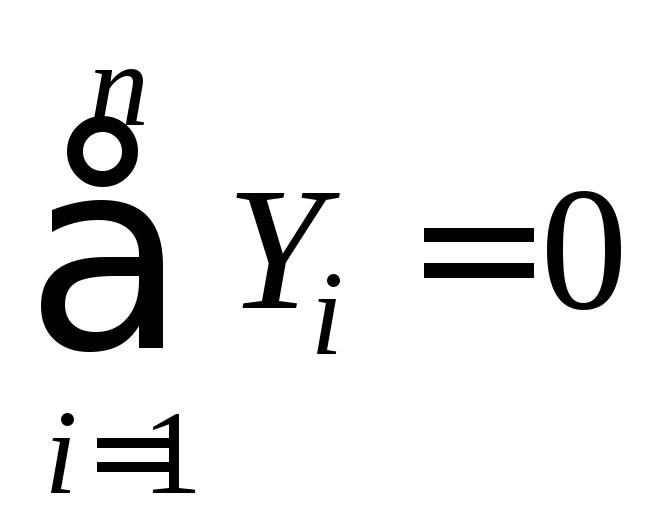 пользоваться
проще, но оно дает надежную проверку
только в тех случаях, когда к балке не
приложены сосредоточенные моменты.
пользоваться
проще, но оно дает надежную проверку
только в тех случаях, когда к балке не
приложены сосредоточенные моменты.
3. Перед составлением уравнений равновесия нужно выбрать (вообще говоря, произвольно) направления реакций и изобразить их на рисунке. Если в результате вычислений какая-либо реакция получается отрицательной, нужно изменить на рисунке ее направление на обратное и в дальнейшем считать эту реакцию положительной,
5. Если на балку действует распределенная нагрузка, то для определения реакций ее заменяют равнодействующей, которая равна площади эпюры нагрузки и приложена в центре тяжести этой эпюры.
Пример 5. Вычислить опорные реакции для балки, показанной на рис. 8.
Прежде всего находим равнодействующие Р1 и Р2 нагрузок, распределенных на участках АС н СВ:
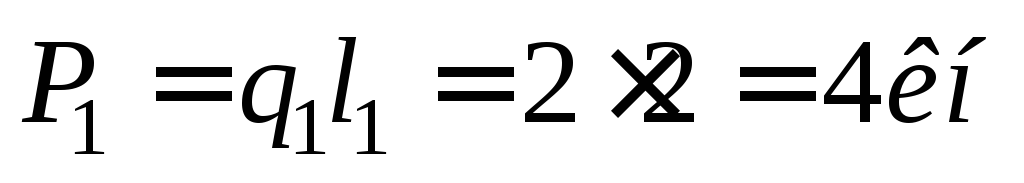 ;
; 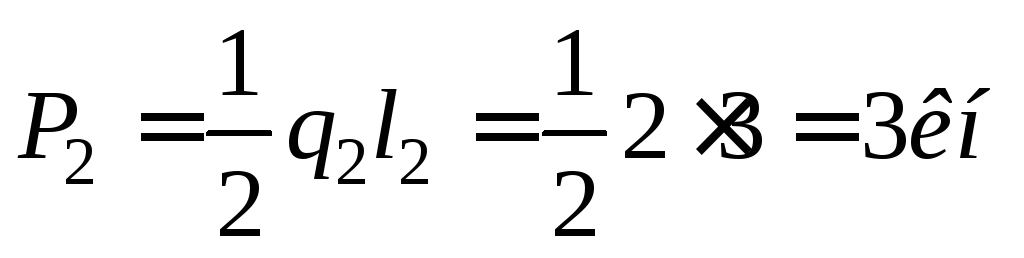 .
.
Сила Р1 приложена в центре тяжести прямоугольника, а Р2 — в центре тяжести треугольника. Находим реакции:
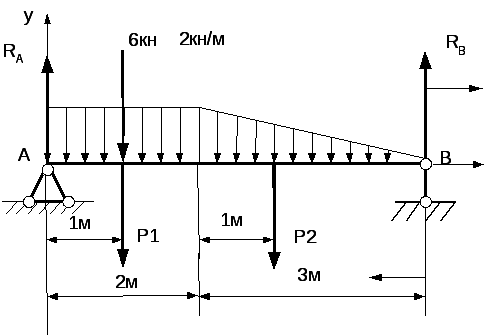
Рис 8
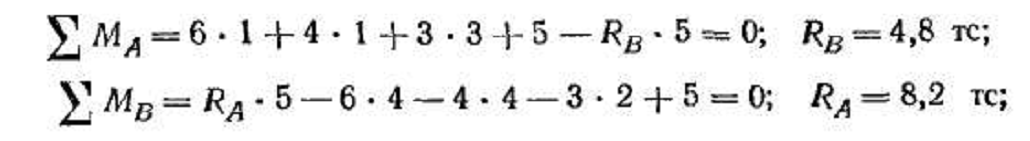
Проверка: