Активное давление грунта
Давление сыпучего грунта на вертикальную подпорную стенку при отсутствии трения на задней гране
Для
решения данной задачи вырезаем в массиве
грунта на глубине Z призму с главными
площадками. В момент предельного
состояния условия равновесия для
песчаного грунта могут быть записаны
в следующем виде: 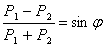
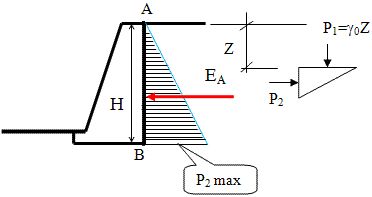
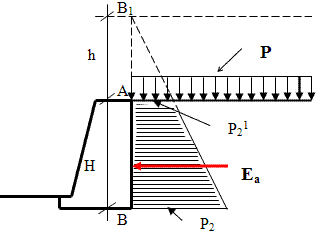
Расчётная схема для определения максимальной величины активного давления сыпучего грунта на массивную подпорную стенку.
Тогда из данного уравнения можно записать соотношения между главными нормальными напряжениями:
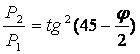
После
преобразования, с учётом принятых
обозначений на схеме, получим: 
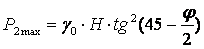
Величина активного давления грунта на подпорную стенку ЕА равна площади эпюры Р2 и составит:

Тогда получим следующее выражение для активного давления грунта на вертикальную подпорную стенку при горизонтальной отсыпке:
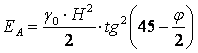
Учёт сцепления для глинистого грунта
В данном случае рассматривается та же, что и вышеприведенная задача, но для глинистого грунта (глинистый грунт обладает трением и сцеплением, стенка гладкая).
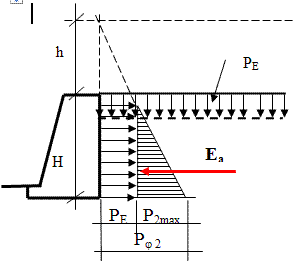
Расчётная схема для определения максимальной величины бокового давления глинистого грунта на вертикальную подпорную стенку.
Сцепление глинистого грунта заменяем эквивалентным давлением РЕ — давлением связности (см. ранее).
Тогда из условия сопротивления грунта сдвигу, можно записать:

Вертикальное давление РЕ – заменяем некоторым фиктивным слоем грунта h и получим:
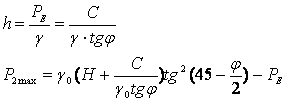
Подставляя РЕ и производя вычисления, окончательно будем иметь:
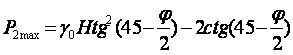 ,
где первое слагаемое учитывает трение
Рφ2 , а второе Рс2 – влияние сцепления. Или в общем виде:Р
,
где первое слагаемое учитывает трение
Рφ2 , а второе Рс2 – влияние сцепления. Или в общем виде:Р
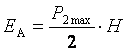
Давление сыпучего грунта на вертикальную подпорную стенку при отсутствии трения по задней гране, с учетом влияния сплошной равномерно распределенной нагрузки
Решение данной инженерной задачи производиться по той же методике, что и в предыдущем случае. При этом сплошную равномерно распредёленную нагрузку (складирование материалов, установка строительной техники и т.д.) представим как некоторый слой грунта давлением Р = γ0h, или получим h=P/γ0, где h следует рассматривать как некоторый фиктивный слой.
Расчётная схема для определения максимальной величины бокового давления сыпучего грунта на вертикальную подпорную стенку с учётом дополнительной равномерно распределённой нагрузки.
В результате получим:

Величина активного давления грунта на подпорную стенку Еа равна площади эпюры Р2 (приложена в ц.т. трапеции) и составит:
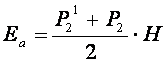
Подставляем значения Р2‘и Р2 в данное выражение и получим:
h=P/γ0; где γ0 — удельный вес грунта засыпки
Определение активного и пассивного давлений грунта.
Активное давление.
Рассмотрим
простейший случай активного давления
при горизонтальной поверхности
однородного грунта и гладкой вертикальной
грани стенки, контактирующей с грунтом.
Элемент грунта, выделенный вертикальными
и горизонтальными площадками (рис. 6.3,
а), примыкающий к гладкой грани (τ = 0),
будет являться главным элементом. На
гранях этого элемента действуют главные
напряжения σ

Рис. 6.3. Активное давление грунта на вертикальную гладкую стенку:
а — главный элемент грунта у стенки в призме обрушения;
б, в — давление несвязного грунта; г, д — то же, связного грунта.
Учитывая, что при
смещении стенки от грунта σx уменьшается, а σz остается неизменным (σ
еа = σx = σ3 = σ1∙tg2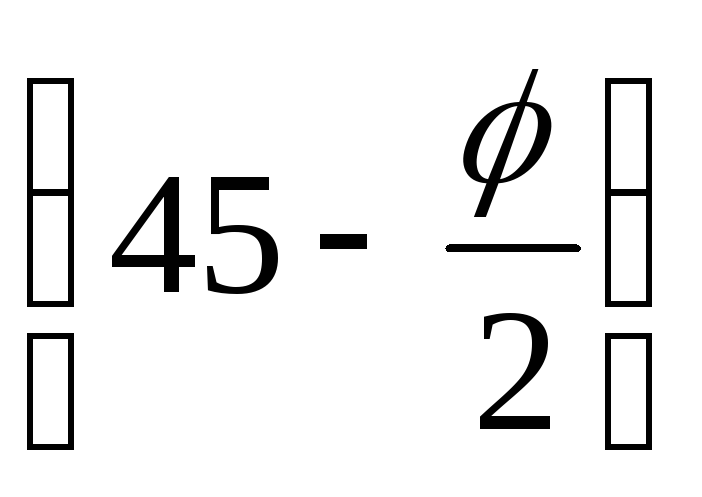
 =
= = (q
+ γгр z)tg2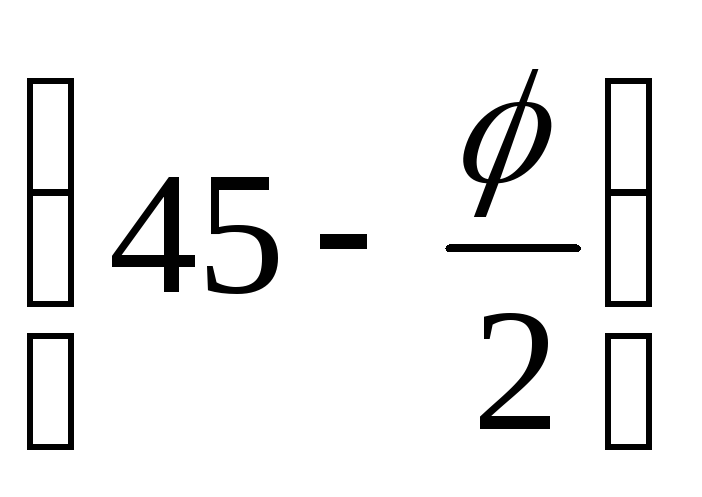 —
2c∙tg
—
2c∙tg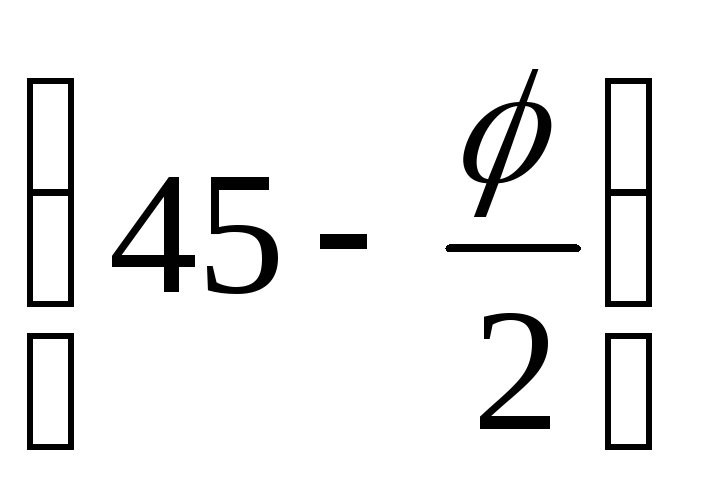 .
(6.1)
.
(6.1)
По зависимости
(6.1) в случае несвязного грунта (с =
0) при q
> 0 эпюра интенсивности активного
давления будет трапецеидальной (рис.
6.3, б), при q
= 0 — треугольной (рис. 6.3, в), а
равнодействующая активного давления,
численно равная площади эпюры е
Еа = 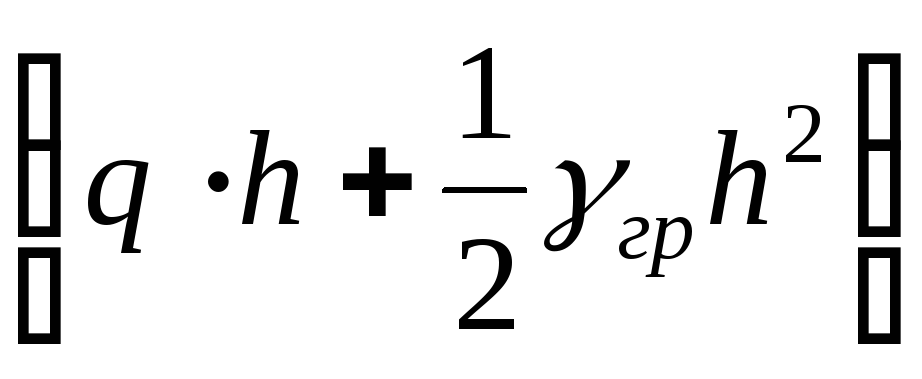 tg2
tg2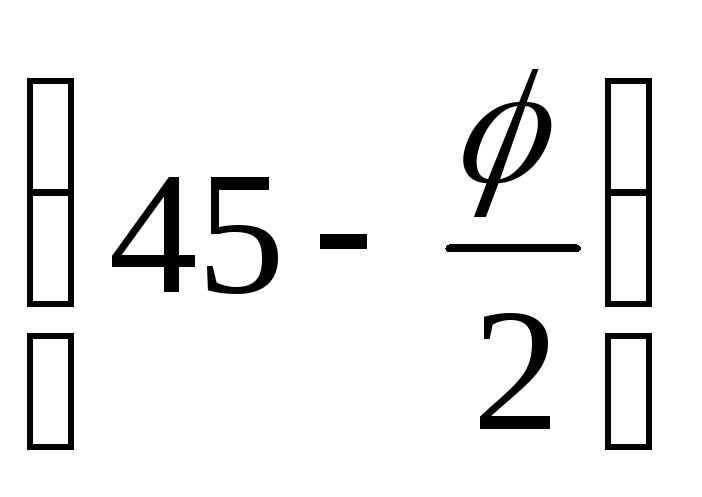 .
(6.2)
.
(6.2)
Как и давление покоя Е0, давление Еа, определяемое по формуле (6.2) и другим (см. ниже), является суммарным давлением (равнодействующей давления) на единицу длины (обычно на 1 погонный метр) стены в направлении, перпендикулярном плоскости хz.
Как показывают
эксперименты, выполненные с несвязными
грунтами, треугольная («классическая»)
эпюра активного давления при q
= 0 (рис. 6.3,в) наблюдается, если контактная
грань стены по всей высоте получает
смещение U ≥ U
Для связного грунта при q = 0 зависимость (6.1) дает в верхней части отрицательные значения давления (рис. 6.3, г), т.е. формально не грунт давит на стенку, а стена, смещаясь, как бы тянет за собой грунт, чего, естественно, не может быть в действительности, между стеной и грунтом образуется щель. Это объясняется тем, что при получении зависимости (6.1) принималось существование везде предельного состояния, а на самом деле связный грунт может в пределах высоты, называемой критической, держать вертикальный откос, не находясь в предельном состоянии.
hк = 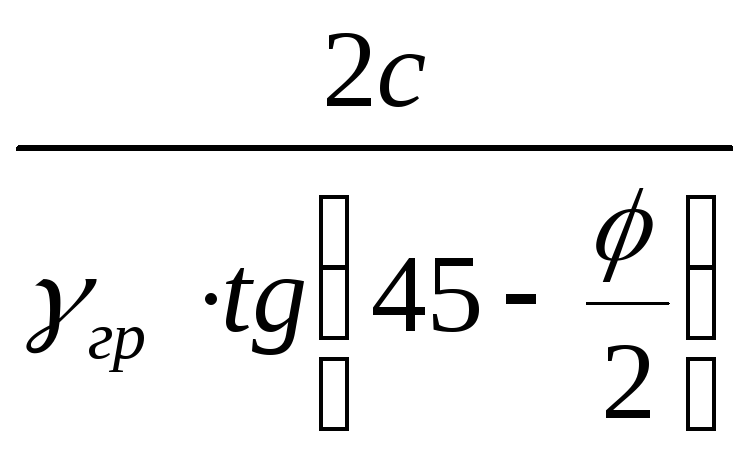 . (6.3)
. (6.3)
Определение активного давления связного грунта следует выполнять, полагая наличие вертикальной щели в пределах высоты hк (рис. 6.3, д). При q = 0 суммарное активное давление с учетом (6.1) и (6.3) определяется как площадь треугольника на рис. 6.3, д по зависимости
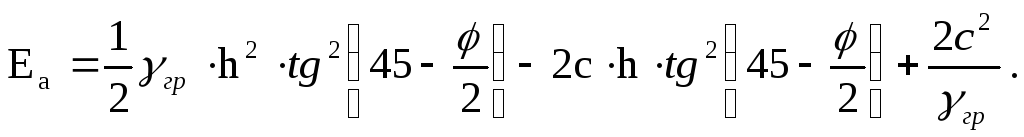
При смещении стенки от засыпки в ней образуется призма обрушения, сползающая по поверхности скольжения, наклоненной к горизонтали под углом (450 + φ/2) (рис. 6.3, а), который легко определяется при использовании построения круга Мора для предельного состояния грунта (см. раздел 3.2, рис. 3.4). Призма обрушения на поверхности засыпки имеет размер
l = mn = h∙tg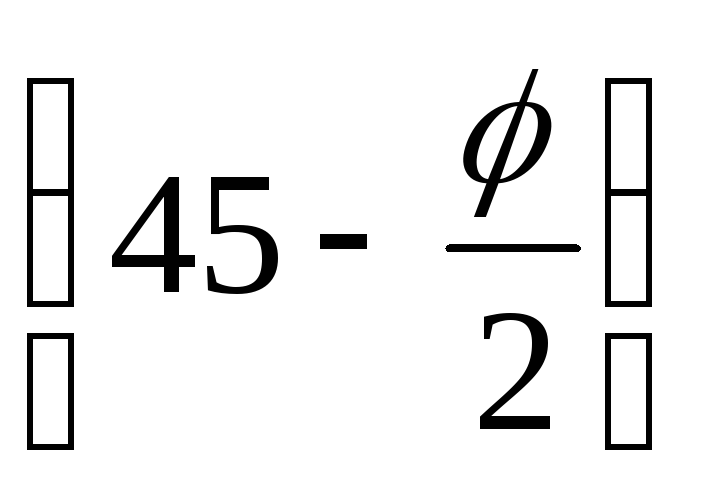 .
.
Изложенный способ определения ea(z) и Ea справедлив только для случая однородной засыпки грунта за стенкой. Для более сложных случаев засыпки и нагрузок применяют различные инженерные приемы, некоторые из них приводятся ниже.
При наличии горизонта грунтовых вод (ГГВ) в случае засыпки из несвязного грунта угол внутреннего трения φ практически не меняется и необходимо учитывать только взвешивание грунта водой, т.е. ниже ГГВ должен приниматься удельный вес взвешенного в воде грунта γвзв (см. раздел 3.3). Тогда активное давление в т.2 (рис. 6.4, а) будет
ea (2) = γгрh/ ∙tg2 ,
,
а в т.3 — ea (3) = (γгр∙h/ + γвзв ∙h// )∙tg2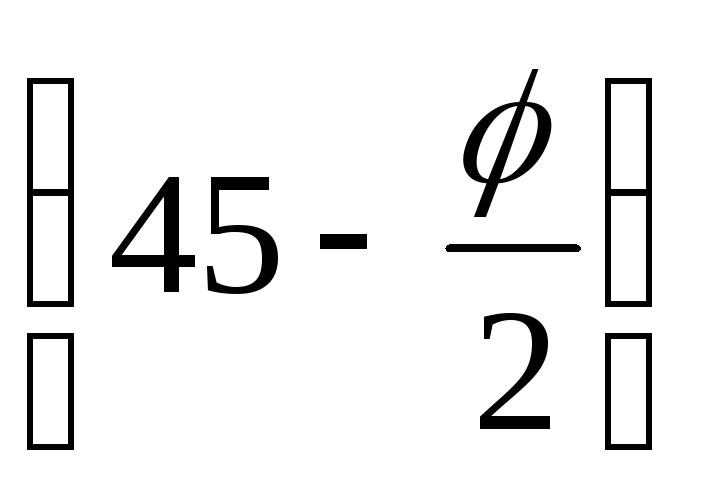 .
.
Эпюра активного давления в т.2 имеет излом тем больший, чем больше разница между γгр и γвзв.
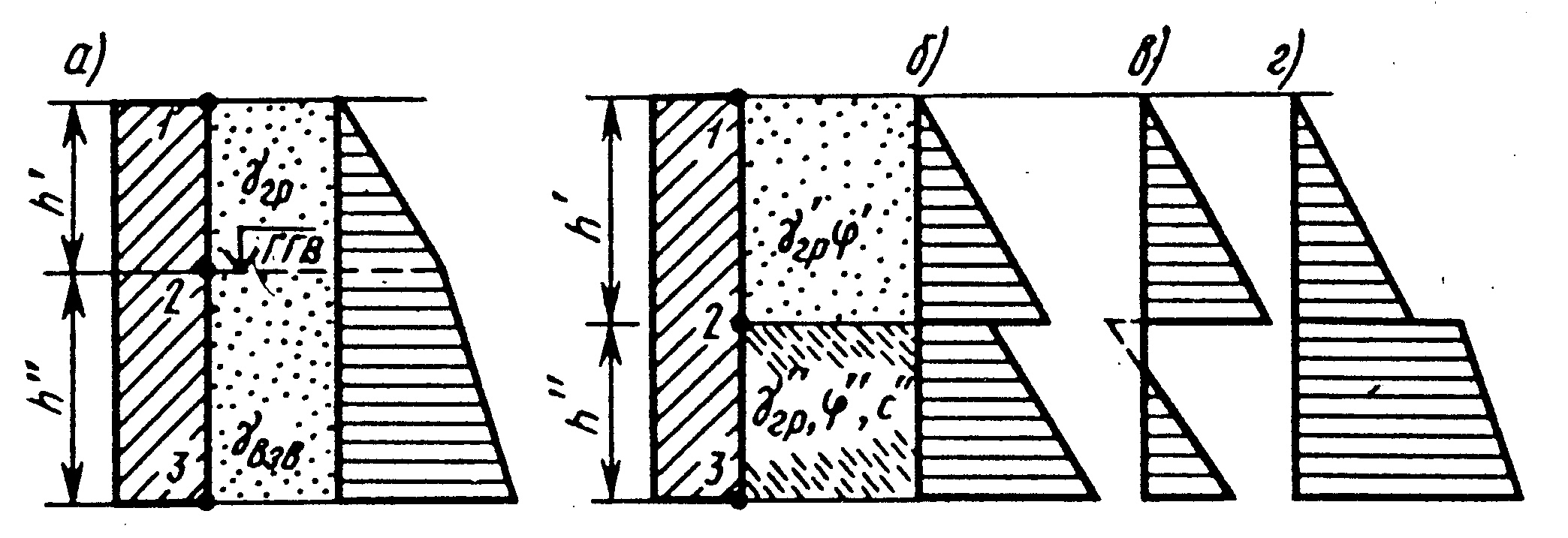
Рис. 6.4. Влияние горизонта грунтовых вод (а) и
слоистости засыпки (б) на активное давление.
При слоистой
засыпке в
каждой точке перехода из слоя в слой
должны определяться две величины
давления, в точках немного выше и ниже
границы раздела слоев. Так, для схемы
на рис. 6.4,б в т.2 активное давление будет:
выше границы — ea = γ/гр∙h/ ∙tg2 ,
ниже границы — ea = γ/гр∙h/ ∙tg2
,
ниже границы — ea = γ/гр∙h/ ∙tg2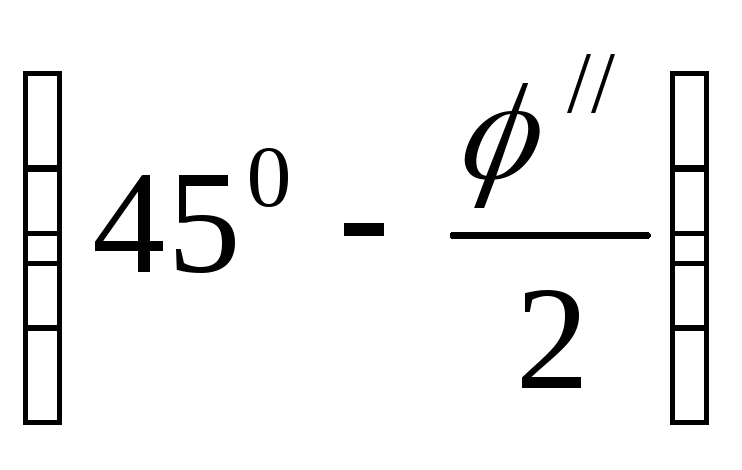 —
2c//∙tg
—
2c//∙tg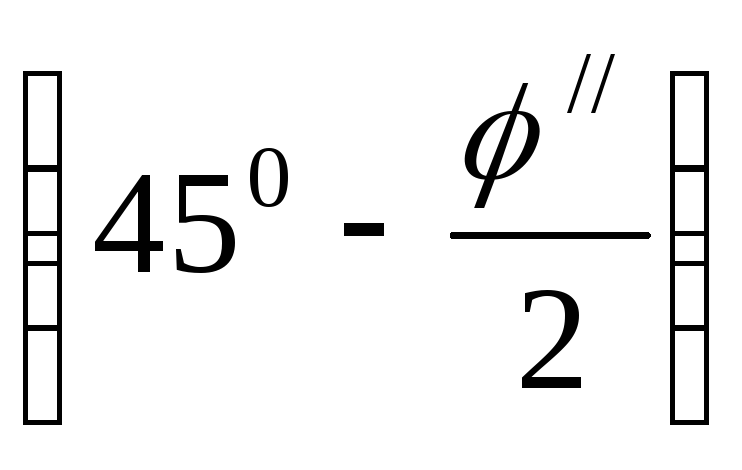 .
B результате на эпюре в т.2 возникает
скачок давления, причем если грунт
нижележащий прочнее вышележащего, то
скачок направлен в сторону уменьшения
давления (рис. 6.4, б, в) и наоборот (рис.
6.4, г). При большой величине с возможно даже получение отрицательного
давления ea (рис.6.4, в), что свидетельствует о
способности связного грунта держать
на этом участке вертикальный откос с
образованием условной щели.
.
B результате на эпюре в т.2 возникает
скачок давления, причем если грунт
нижележащий прочнее вышележащего, то
скачок направлен в сторону уменьшения
давления (рис. 6.4, б, в) и наоборот (рис.
6.4, г). При большой величине с возможно даже получение отрицательного
давления ea (рис.6.4, в), что свидетельствует о
способности связного грунта держать
на этом участке вертикальный откос с
образованием условной щели.
Показанные на рис. 6.3 и 6.4 эпюры получены, исходя из соотношения (3.20/) между главными напряжениями, записанного в форме (6.1) для определения интенсивности активного давления ea и затем величины равнодействующей Ea. В более сложных случаях (наклонная поверхность грунта и грань стенки и т.п.) использование зависимости (6.1) становится невозможным и широкое распространение получил метод Кулона, основанный на гипотезе плоской поверхности скольжения.
В расчетной схеме метода Кулона принимается, что грунт несвязный, поверхность скольжения плоская (рис. 6.5, а).
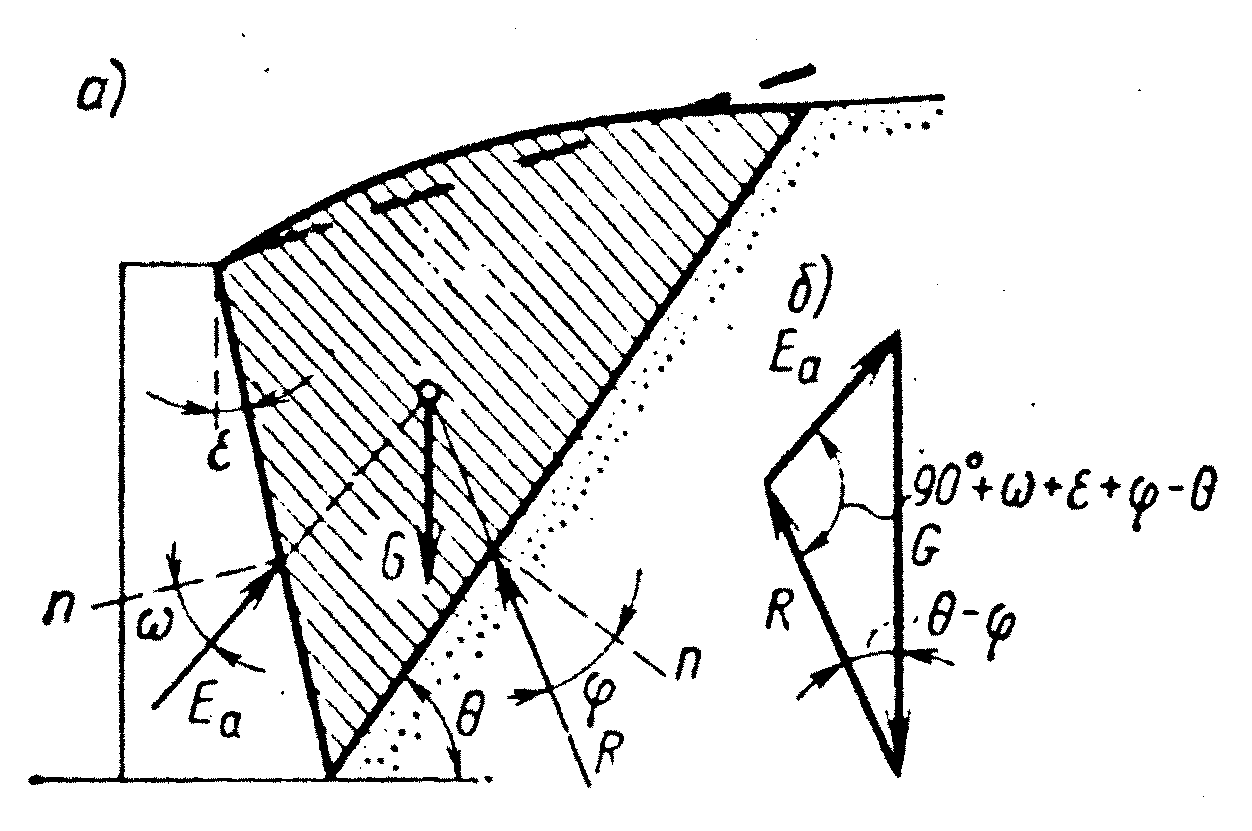
Рис. 6.5. Расчетная схема метода Ш. Кулона.
По плоскости обрушения принимается состояние предельного равновесия, т.е. выполняется условие Кулона, в соответствии с чем равнодействующая R напряжений на поверхности скольжения отклоняется от нормали к ней на угол внутреннего трения грунта φ. При учете трения грунта о шероховатую грань стенки равнодействующая активного давления Ea принимается отклоненной от нормали к поверхности стены на заданный угол ω, который обычно меньше φ (в случае гладкой стены ω = 0). На выделенную призму обрушения действуют силы Ea, R, известные по направлению, и вес призмы G, который при принятом угле наклона плоскости скольжения θ известен по направлению и величине. Величина Ea легко находится из условия равновесия, т.е. из условия замыкания силового треугольника на рис. 6.5, б. В треугольнике стороны относятся как синусы противоположных углов, откуда
Ea = G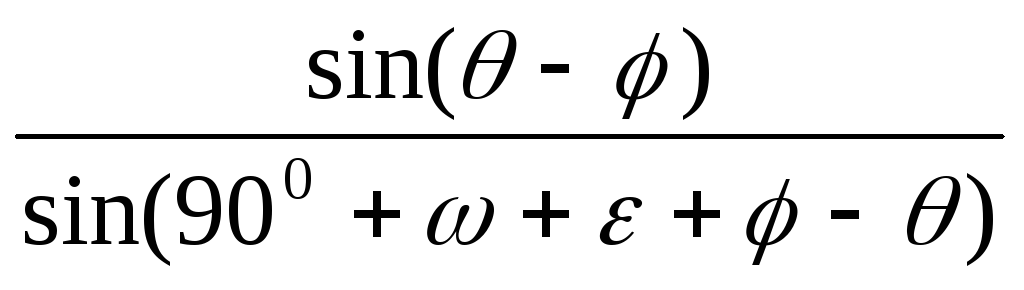 ,
(6.4)
,
(6.4)
где ε — угол, образуемый тыловой (контактной с грунтом) гранью стены с вертикальной плоскостью (рис. 6.5, а).
Анализ зависимости (6.4) показывает, что Ea как функция угла θ имеет эстремум (максимум). Экстремальное значение Ea и принимается за истинную величину активного давления. Отвечающий истинному давлению угол θ находим из условия
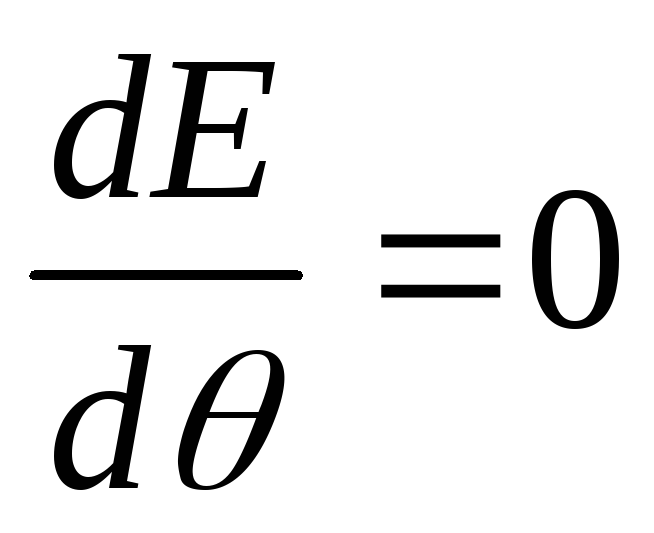 .
(6.5)
.
(6.5)
Задача определения активного давления по зависимости (6.4) при подстановке θ из условия (6.5) для простых случаев, например, для плоской наклонной поверхности засыпки (рис. 6.5, а, пунктир), решается аналитически. Величина Ea определяется по формуле
Еа = 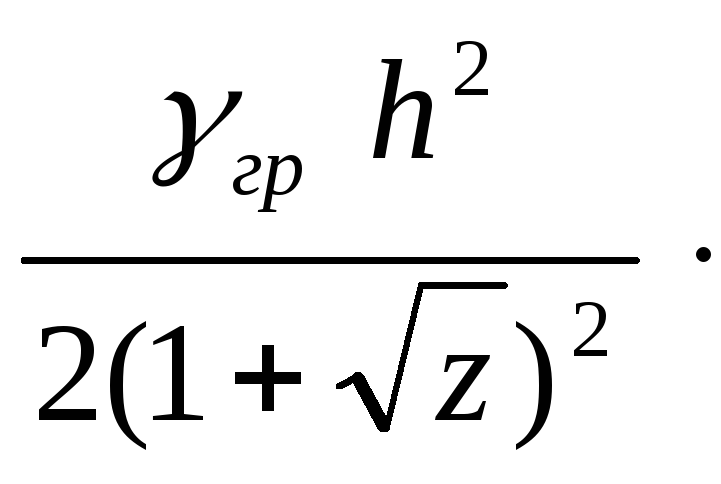
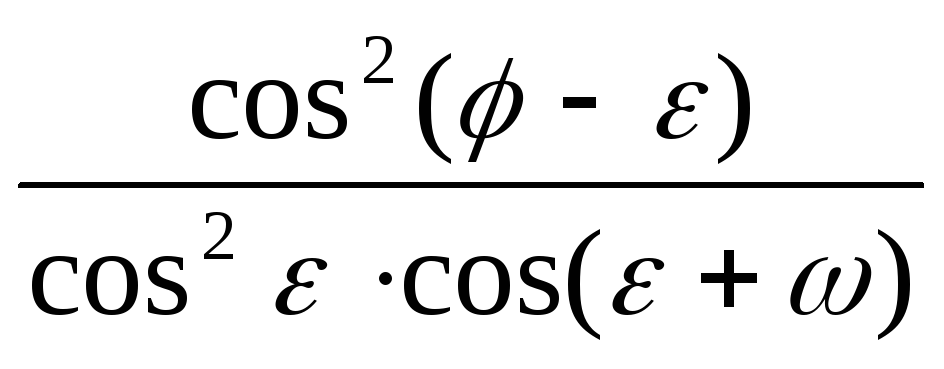 , (6.6)
, (6.6)
где
z
= 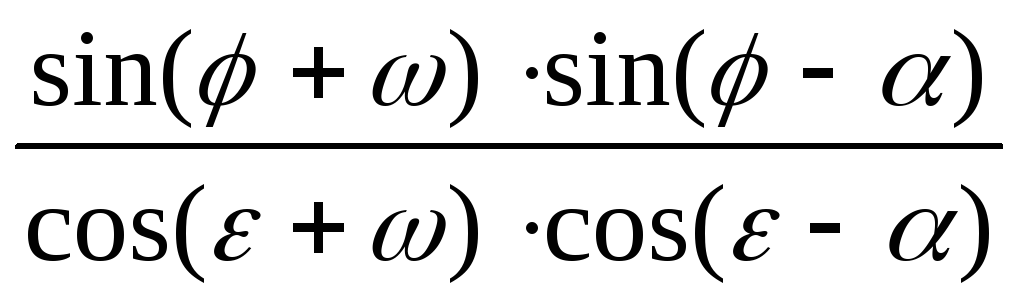 ,
,
α — угол наклона поверхности засыпки к горизонту, причем в случае восходящего откоса (рис. 6.5, а, пунктир) α > 0, в случае нисходящего (падающего) откоса α < 0.
При значениях α =
0, ω = 0, ε = 0 из зависимости (6.5) получаем
θ = 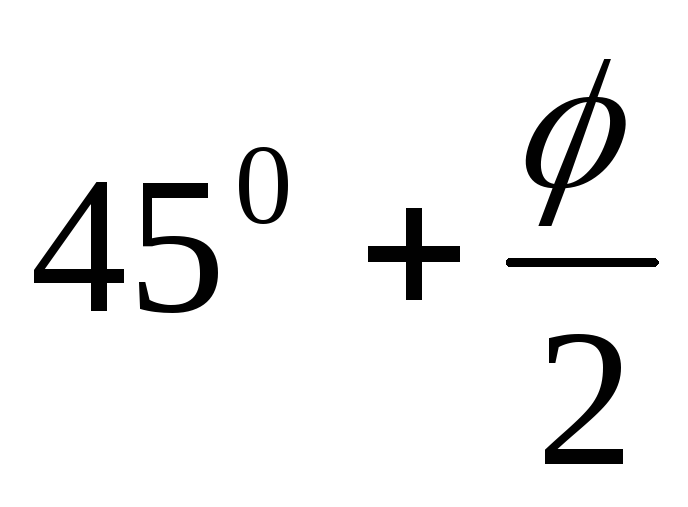 и
суммарное активное давление Еа по зависимости (6.4) совпадает с величиной
Еа по формуле (6.2).
и
суммарное активное давление Еа по зависимости (6.4) совпадает с величиной
Еа по формуле (6.2).
Графические решения задачи поиска θ с наибольшим Еа позволяют получить активное давление в более общих случаях неплоской поверхности засыпки и действующих на поверхность внешних нагрузок. На рис. 6.6 представлен графический способ К. Кульмана. В этом способе проводятся последовательно поверхности скольжения под разными углами θ (рис. 6.6, а) и строятся соответствующие силовые треугольники (рис. 6.6, б). При построении любого треугольника известны величина и направление G (в G включаются вес грунта и внешние нагрузки, попадающие в призму обрушения при соответствующем принятом θ), направления R и Еа (принимаются также, как и в методе Кулона). В результате построений получают огибающую всех величин Еа, проводят к ней вертикальную касательную, что соответствует выполнению условия (6.5), и находят искомое максимальное значение Еа.
Заметим, что в способах Кулона и Кульмана получают только равнодействующую активного давления. Эпюру давления обычно принимают треугольной формы с давлением, линейно нарастающим с глубиной.

Рис. 6.6. Графическое определение активного давления по К. Кульману.
Пассивное давление.
При принудительном смещении (внешними нагрузками) стены на грунт в главном элементе у гладкой грани стенки (рис. 6.3, а) возникающие горизонтальные напряжения σx превышают вертикальные σz, т.е. в этом случае σx = σ1, σz = σ3. Поэтому условие предельного равновесия элемента принимаем в форме (3.20) и для интенсивности пассивного давления получаем зависимость
eп = σz ∙tg2(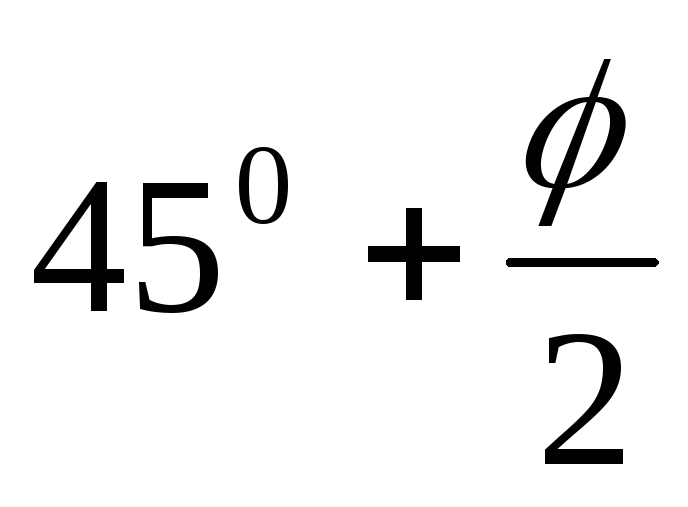 )
+ 2c∙tg(
)
+ 2c∙tg(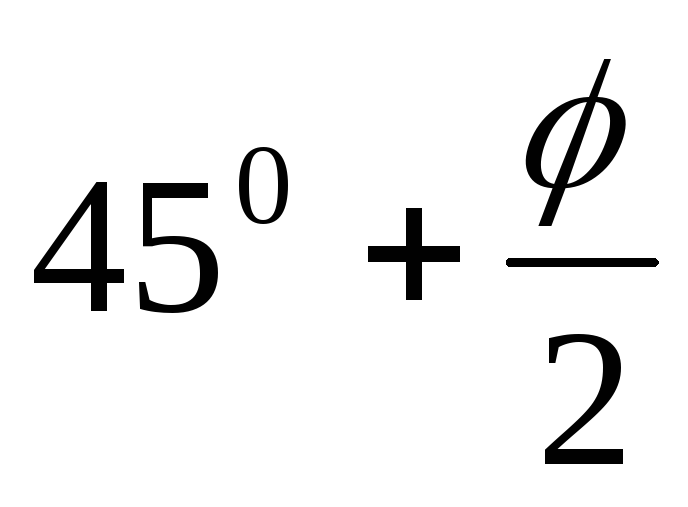 ).
).
Для схемы рис. 6.3, а имеем σz = q + γгр∙z и величину
eп = (q
+ γгр∙z)tg2(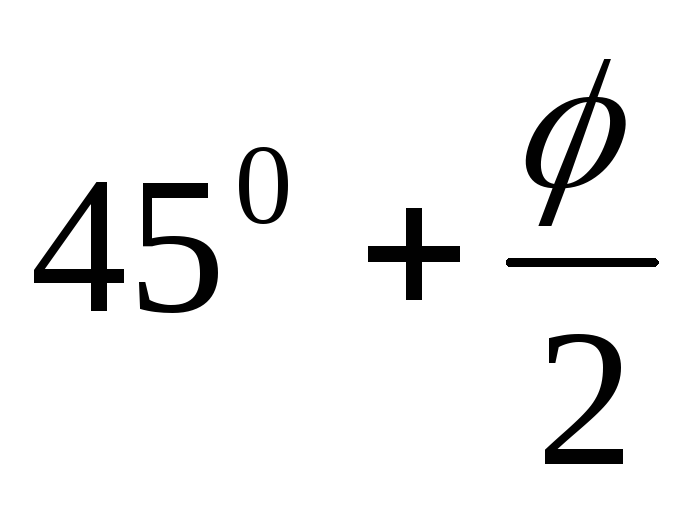 )
+ 2c∙tg(
)
+ 2c∙tg(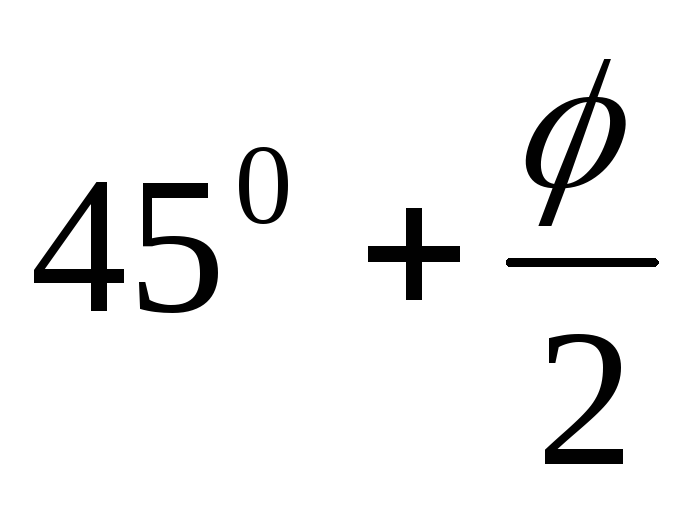 ),
(6.7)
),
(6.7)
a равнодействующая пассивного давления определяется выражением
Eп = (q∙h
+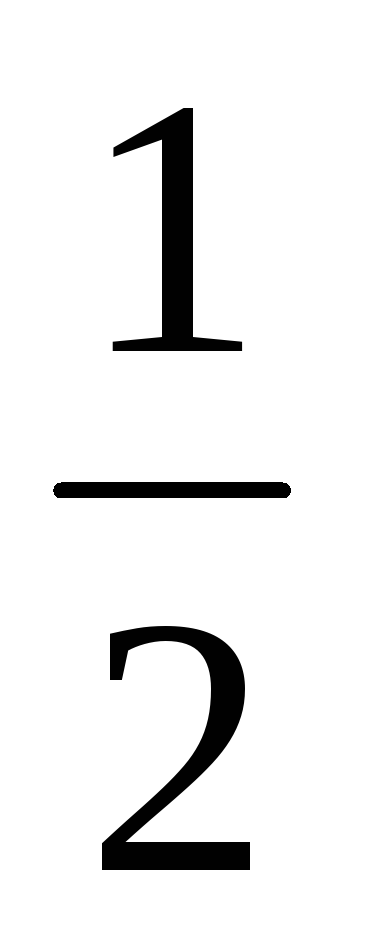 γгр∙h2)
tg2(
γгр∙h2)
tg2(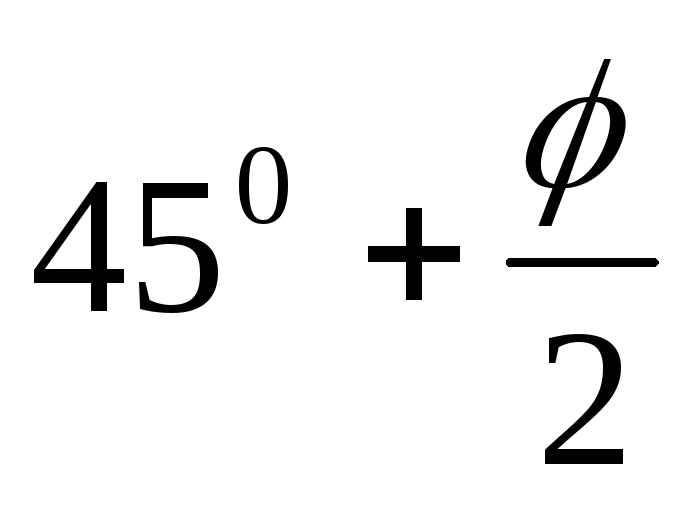 )+
2c∙h∙tg(
)+
2c∙h∙tg(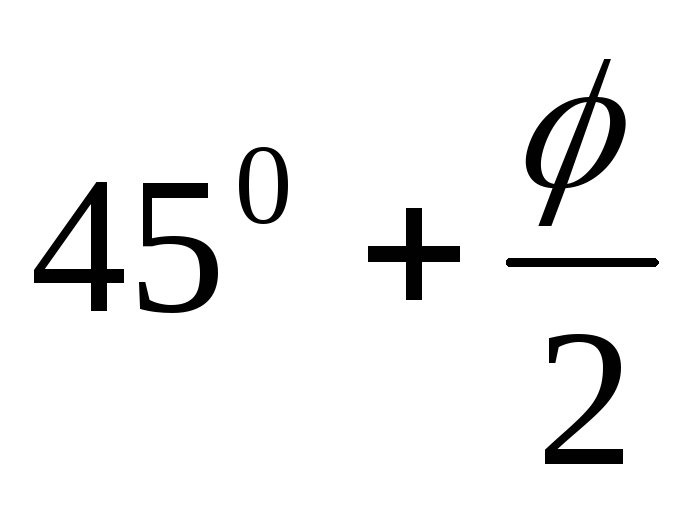 ).
(6.8)
).
(6.8)
В
случае несвязного грунта (с = 0) и отсутствии нагрузки q
на поверхности засыпки эпюра пассивного
давления будет согласно (6.7) треугольной,
а при наличии нагрузки q
или сцепления с ≠ 0 — трапецеидальной. Заметим, что
при q = 0, с = 0 и
φ = 300 величина пассивного давления
eп = γгр∙z∙tg2600 превышает в 9 раз величину активного
давления ea = γгр∙z∙tg2300.
Поверхность скольжения, ограничивающая
призму выпора, наклонена к горизонту
под углом θ = 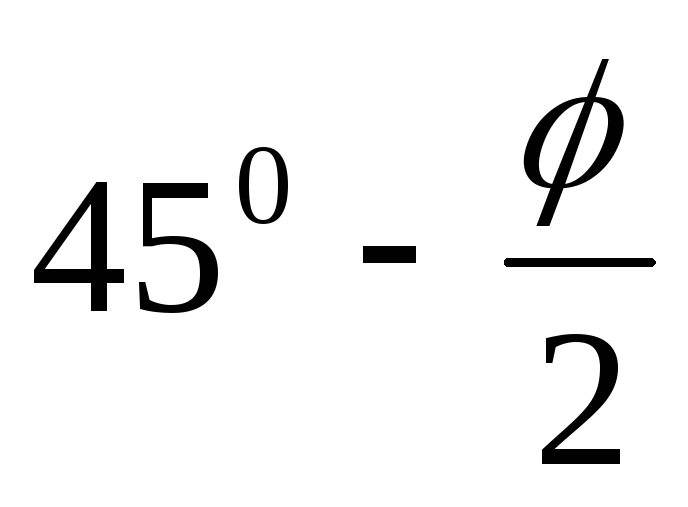 .
.
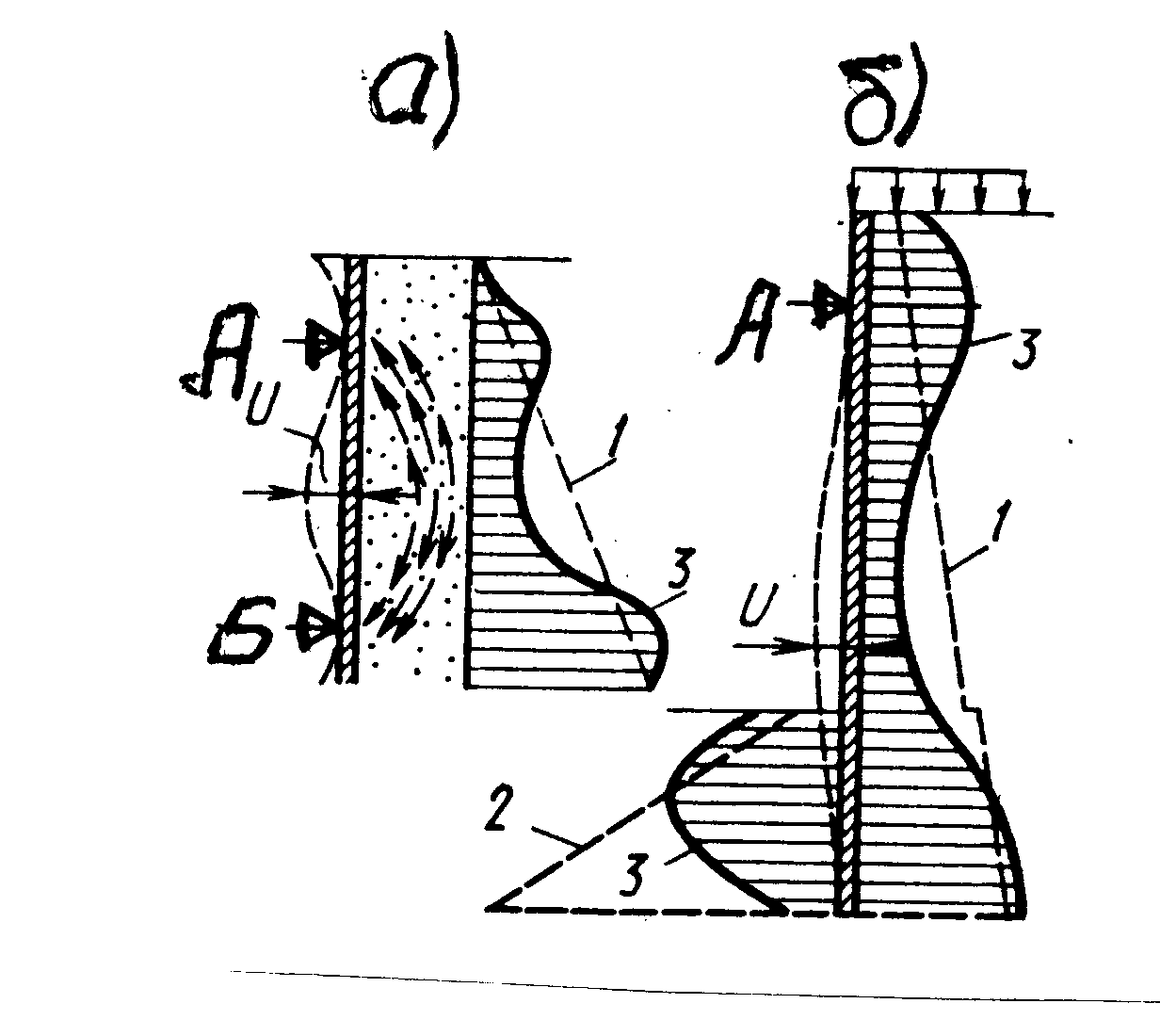
Рис. 6.7. Влияние гибкости стены на давление грунта:
1, 2 – активное и пассивное давление по методу Кулона,
3 – эпюры наблюдаемых давлений
Для определения пассивного давления в случае шероховатых наклонных стен и наклонной поверхности грунта может также применяться расчетная схема Кулона, в которой принимается выпор грунта по плоской поверхности скольжения. Расчетная схема аналогична приведенной на рис. 6.5 с учетом, что силы трения по поверхности скольжения имеют противоположное случаю активного давления направление. Поэтому зависимость, аналогичная (6.4), в этом случае принимает вид
Еп = G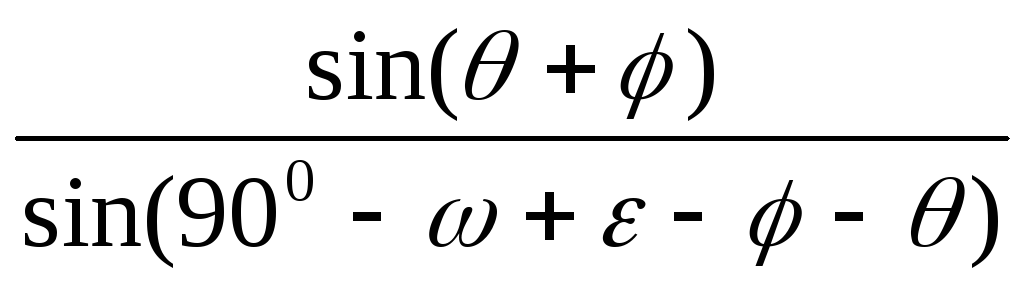 .
.
Для определения Еп применим также графический вариант Кульмана с использованием построения, аналогичного приведенному на рис. 6.6 для активного давления при противоположном направлении сил трения по поверхности скольжения.
Приведенные выше способы определения активного и пассивного давлений относятся к жестким массивным сооружениям (стенкам), контактная с грунтом грань которых при смещениях остается плоской.
В случаях изгибаемых сооружений (тонкие стены, шпунтовые ограждения и др.) деформации изгиба существенно влияют на распределение контактных давлений. Так в случае изгибаемой стены (рис. 6.7, а) в местах расположения неподвижных опор (т. А, Б) происходит возрастание давления выше активного, а на участках наибольших горизонтальных смещений U, наоборот, давление становится меньше активного. Это объясняется проявлением «арочного» эффекта в грунтах, вызванного прогибом стенки. При прогибах стены, показанной на рис. 6.7, б, давление перераспределяется по ее высоте: уменьшается в пролетной части, где стена прогибается, и увеличивается (концентрируется) в зоне опоры (т. А) и ниже уровня дна котлована. Действительное очертание эпюры пассивного давления на заглубленном в грунт участке стены также не соответствует рассчитанному по формуле (6.8). Для учета влияния деформаций изгиба стенки на распределение контактного давления на нее были предложены различные инженерные методики решения контактных задач для изгибаемых тонких стенок как сооружений конечной жесткости (глава 4).
В настоящее время при расчетах изгибаемых конструкций, подобных представленным на рис. 6.7, успешно применяются программные комплексы, перечисленные в гл. 4. Наиболее совершенные из них позволяют моделировать тонкие конструкции, определять напряженно-деформированное состояние грунта с учетом формирования областей предельного напряженного состояния.
Определение давления грунта методом теории предельного равновесия (ТПР) выполняется путем численного интегрирования (В.В.Соколовский, 1960) уравнений, включающих в случае плоской задачи два дифференциальных уравнения равновесия (3.2) и уравнение Кулона в форме (3.22). Имеются решения для случая горизонтальной поверхности засыпки из однородного грунта и для различных значений угла ε наклона контактной грани стенки к вертикали и угла трения ω грунта о стенку [12].
В случае стены с гладкой вертикальной контактной гранью, т.е. при ε = 0, ω = 0 (рис. 6.3, а) активное и пассивное давления по решению ТПР совпадает соответственно с величинами давлений по формулам (6.2) и (6.8) приближенного метода (метода Кулона). При значениях ε ≠ 0, ω ≠ 0 отличие в величине активного давления по ТПР и приближенному методу Кулона незначительное и вполне допустимо определять активное давление по зависимости (6.6). Влияние сил трения грунта о стенку и наклона стенки, т.е. углов ω и ε, существенно отражается на величине пассивного давления. Приближенные решения при значительных величинах ω, ε завышают пассивный отпор по сравнению с решением ТПР и к использованию решения Кулона для определения пассивного давления следует относиться осторожно [9].
Пример расчета
Дано:
Высота стенки H=6 м.
Высота заглубления стенки h/=1,5 м.
Угол внутреннего трения грунта φ=160.
Удельный вес грунта γ=22 кН/м3
Решение.
Активное давление грунта на подпорную стенку:
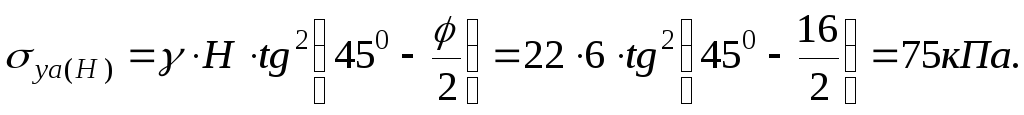
Равнодействующая активного давления:
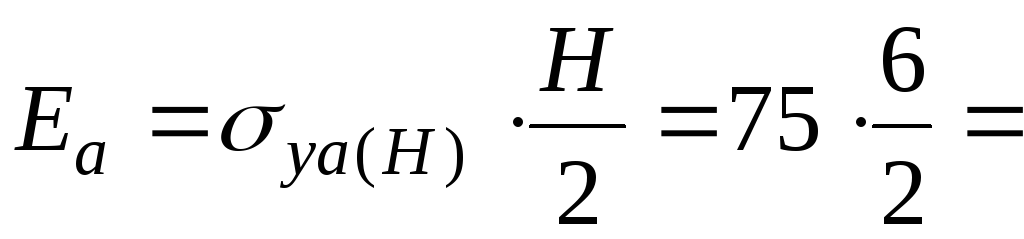 225
кН/м.
225
кН/м.
Пассивное давление грунта на подпорную стенку:
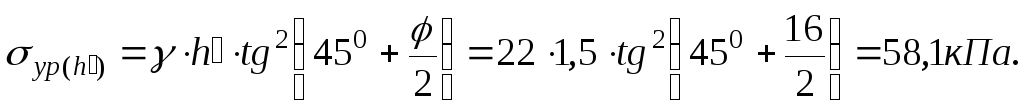
Равнодействующая пассивного давления:
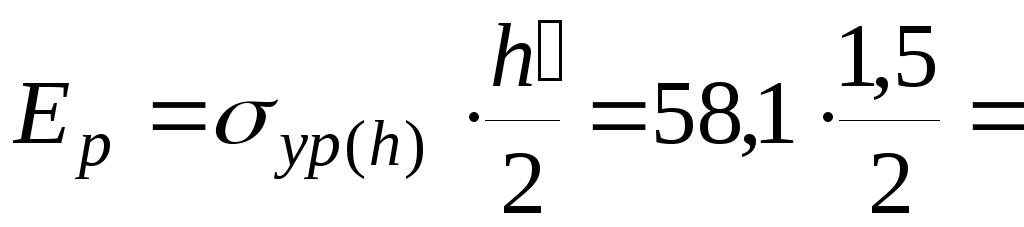 43,58
кН/м.
43,58
кН/м.
По полученным данным строим расчетную схему и эпюру напряжений (рис.3.4.1).
При построении расчетной схемы и эпюр активного и пассивного давлений грунта на подпорную стенку следует принимать масштаб расстояний 1:50, масштаб давлений 0,025 МПа в 1 см.
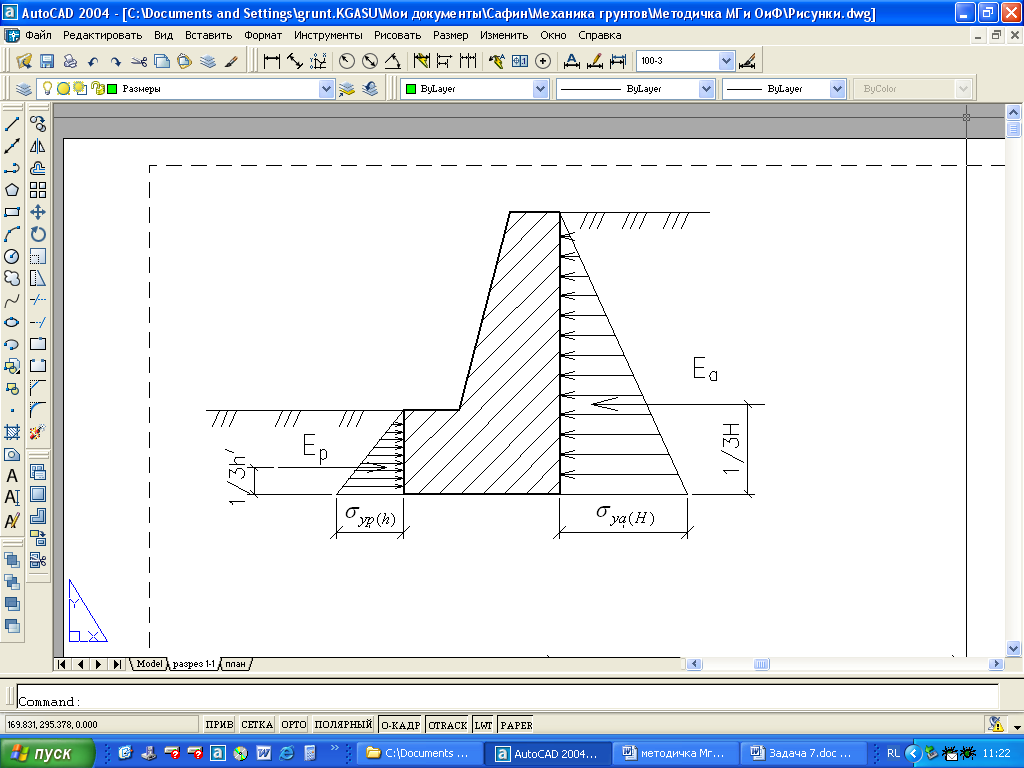
Рис.3.4.1. Расчетная схема подпорной стены
3.4.2. Определение давления на подпорную стенку от идеально сыпучего грунта с учетом пригруза на поверхности грунта
Действие сплошнго равномерно распределенного пригруза в этом случае заменяется эквивалентной высотой слоя грунта, равной:
 . (3.4.6)
. (3.4.6)
Активное давление на уровне верха подпорной стенки:
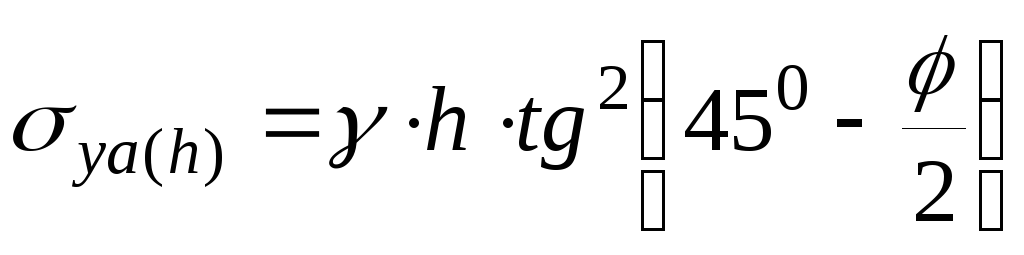 . (3.4.7)
. (3.4.7)
Активное давление на подошве подпорной стенки:
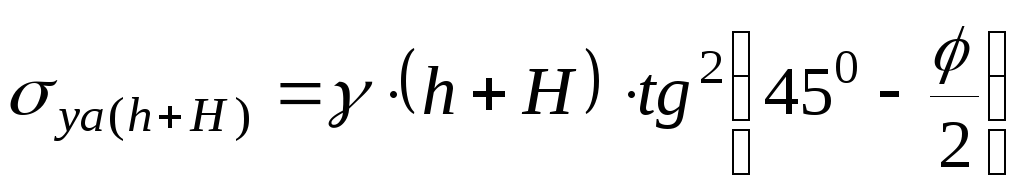 . (3.4.8)
. (3.4.8)
Равнодействующая активного давления:
 . (3.4.9)
. (3.4.9)
Пример расчета
Высота стенки H=6 м.
Высота заглубления стенки h/=1,5 м.
Угол внутреннего трения грунта φ=160.
Удельный вес грунта γ=22 кН/м3.
Интенсивность
пригрузки 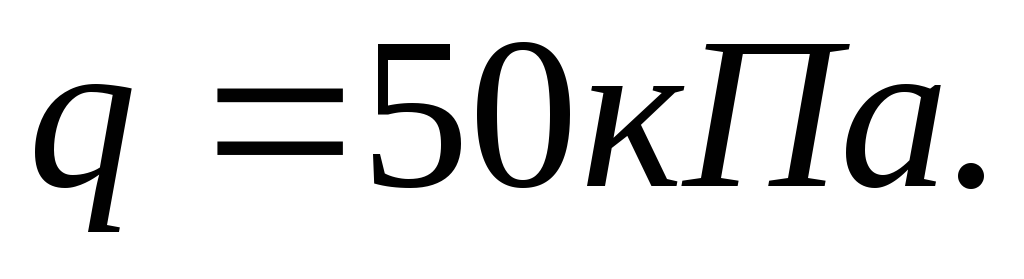
Решение.
Эквивалентная высота слоя грунта:
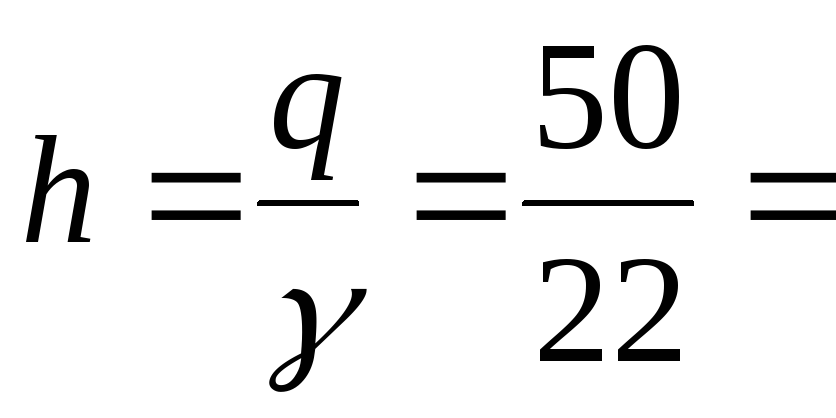 2,27м.
2,27м.
Активное давление на уровне верха подпорной стенки:
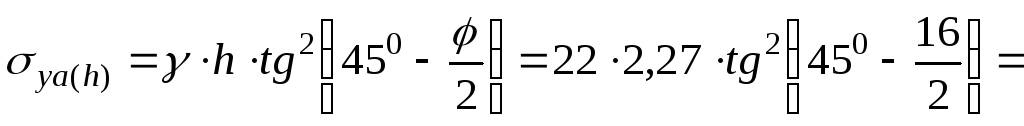 28,36кПа.
28,36кПа.
Активное давление на подошве подпорной стенки:
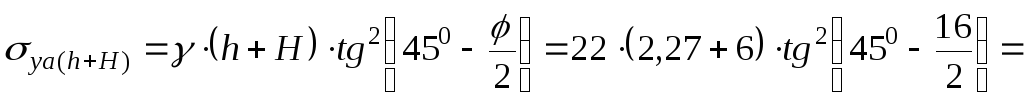 103,33
кПа.
103,33
кПа.
Равнодействующая активного давления:
 395,07
кН/м.
395,07
кН/м.
По полученным данным строим расчетную схему и эпюру напряжений (рис.3.4.2).
При построении расчетной схемы и эпюр активного и пассивного давлений грунта на подпорную стенку следует принимать масштаб расстояний 1:50, масштаб давлений 0,025 МПа в 1 см.

Рис.3.4.2. Расчетная схема подпорной стены с пригрузом
3.4.3. Определение давления на подпорную стенку от связного грунта
Действие сил сцепления заменяется всесторонним давлением связности:
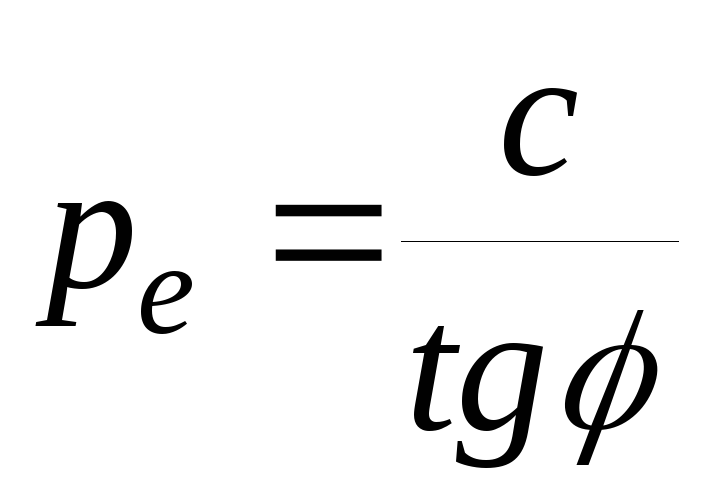 . (3.4.10)
. (3.4.10)
Далее приводим давление связности по вертикали к эквивалентному слою грунта:
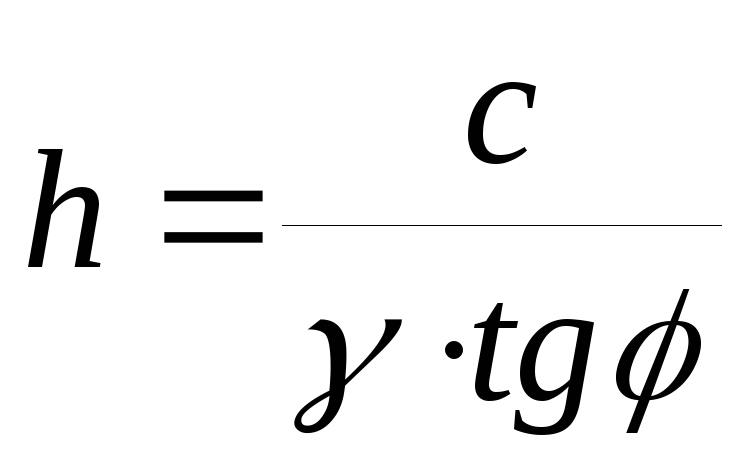 . (3.4.11)
. (3.4.11)
Активное давление на подошве подпорной стенки:
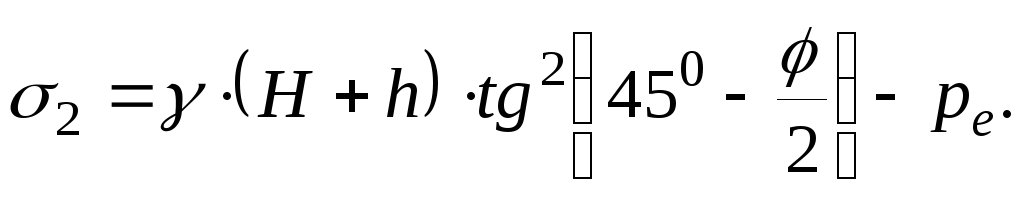 (3.4.12)
(3.4.12)
Подставляя значения и преобразовывая, получаем:
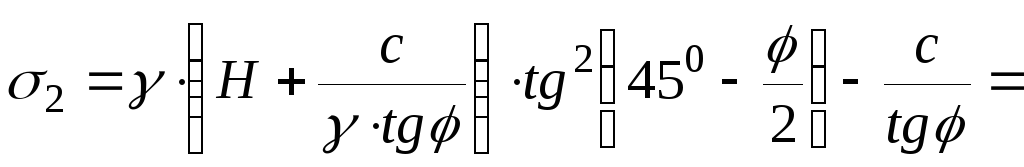
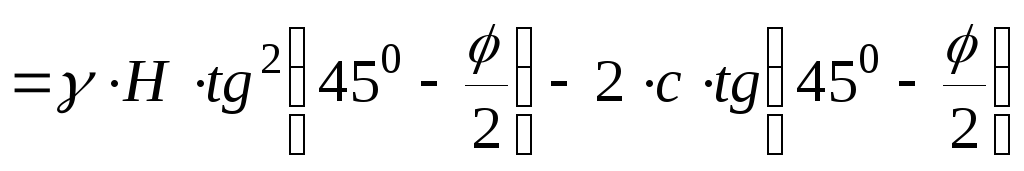 . (3.4.13)
. (3.4.13)
На
некоторой глубине суммарное давление
будет равно нулю, из условия 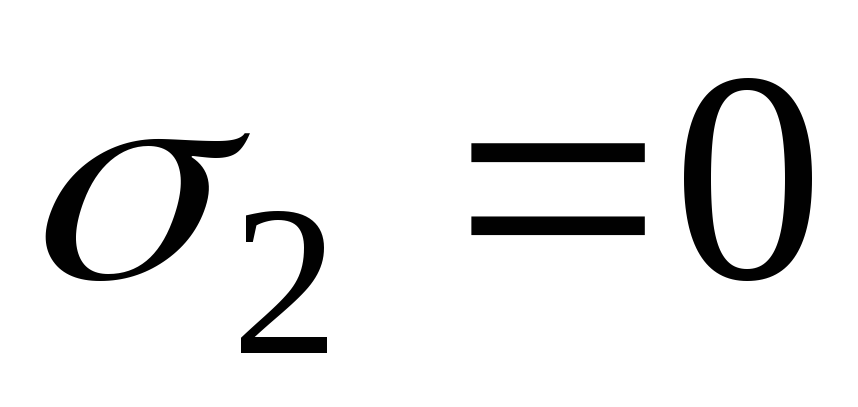 находим высотуhс:
находим высотуhс:
 . (3.4.14)
. (3.4.14)
Равнодействующая активного давления:
 . (3.4.15)
. (3.4.15)
Равнодействующая пассивного давления в связных грунта будет равна:
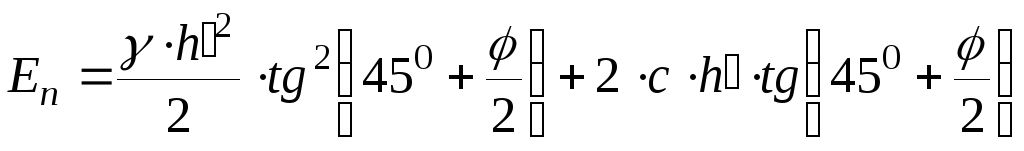 . (3.4.16)
. (3.4.16)
Пример расчета
Высота стенки H=6 м.
Высота заглубления стенки h/=1,5 м.
Угол внутреннего трения грунта φ=210.
Удельное сцепление грунта с=18 кПа.
Удельный вес грунта γ=22 кН/м3.
Решение:
Действие сил сцепления заменяем всесторонним давлением связности:
 46,88
кПа.
46,88
кПа.
Далее приводим вертикальное давление связности к эквивалентному слою грунта:
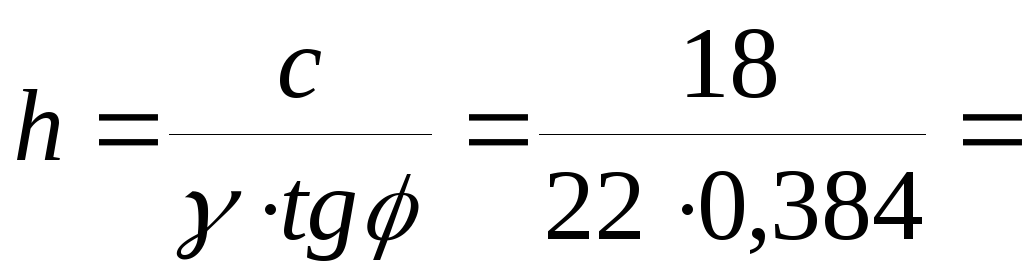 2,13м.
2,13м.
Активное давление на подошве подпорной стенки:
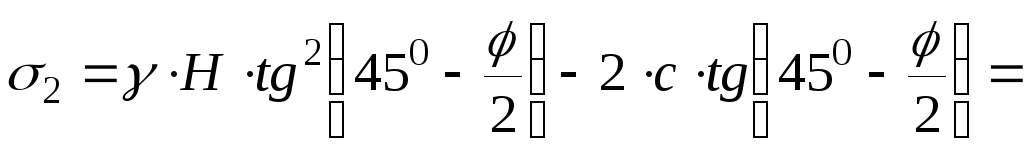
 38,0
кПа.
38,0
кПа.
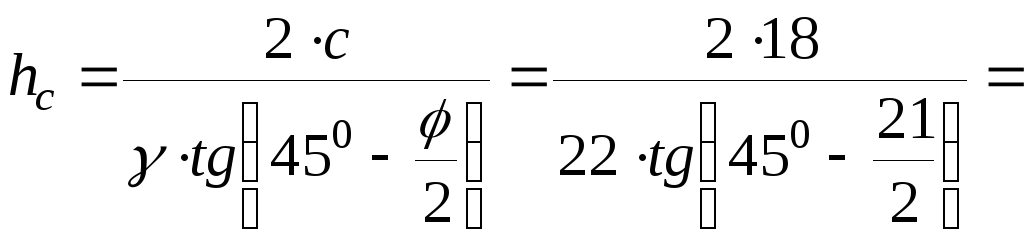 2,37
м.
2,37
м.
Равнодействующая активного давления:
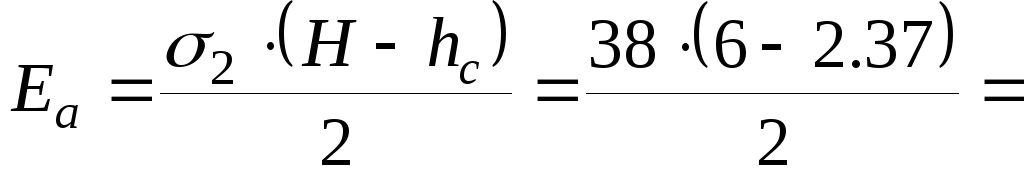 68,97
кН/м.
68,97
кН/м.
Равнодействующая пассивного давления:

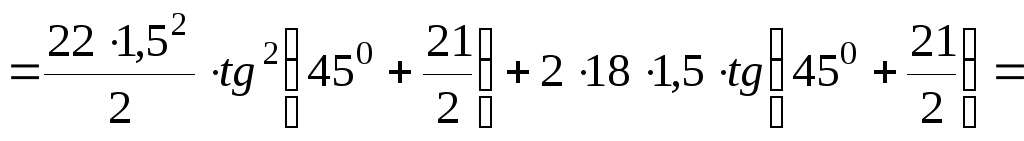 131,59
кН/м.
131,59
кН/м.
По полученным данным строим расчетную схему и эпюру напряжений (рис.3.4.3). При построении расчетной схемы и эпюр активного и пассивного давлений грунта на подпорную стенку следует принимать масштаб расстояний 1:50, масштаб давлений 0,025 МПа в 1 см.
Рис.3.4.3. Расчетная схема подпорной стены
3.5. Задача №5. Расчет осадки методом послойного суммирования
Величину
полной стабилизированной осадки
грунтовой толщи  по методу послойного суммирования
определяют как сумму осадок элементарных
слоев грунта по формуле:
по методу послойного суммирования
определяют как сумму осадок элементарных
слоев грунта по формуле:
 ,
,
где  — среднее напряжение в
— среднее напряжение в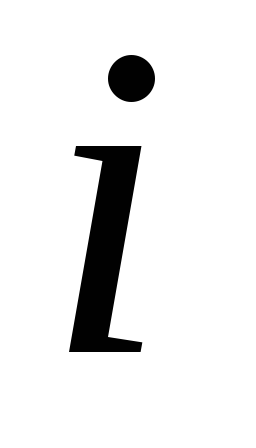 —
ом элементарном слое грунта, равное
полусумме напряжений на верхней
—
ом элементарном слое грунта, равное
полусумме напряжений на верхней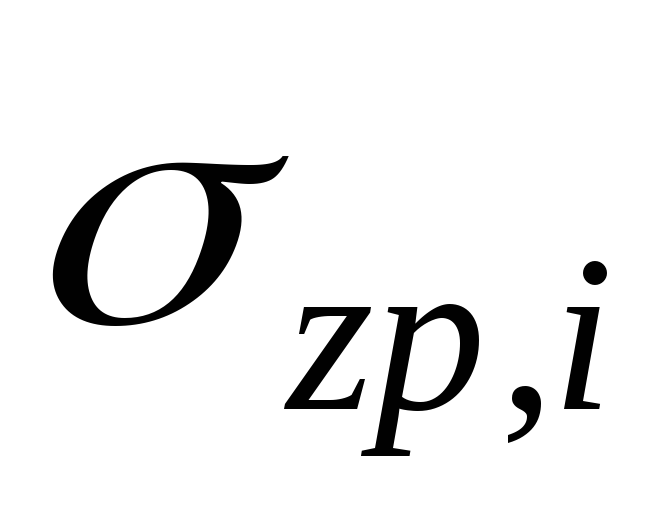 и нижней
и нижней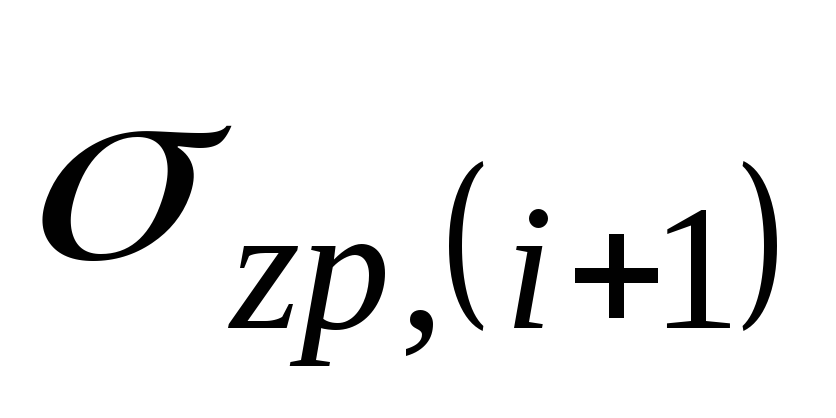 границах этого слоя;
границах этого слоя;
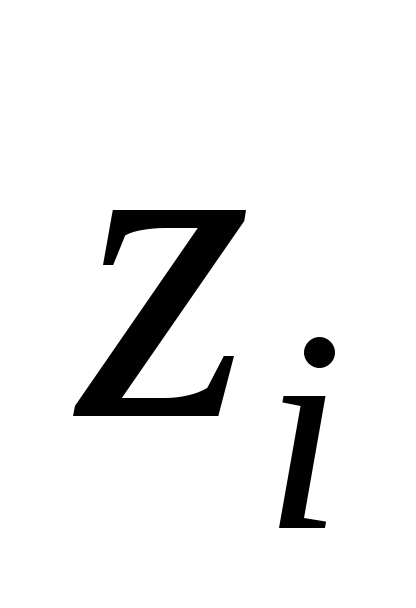 — расстояние от подошвы полосы нагружения
до элементарного слоя;
— расстояние от подошвы полосы нагружения
до элементарного слоя;
 — толщина элементарного слоя;
— толщина элементарного слоя;
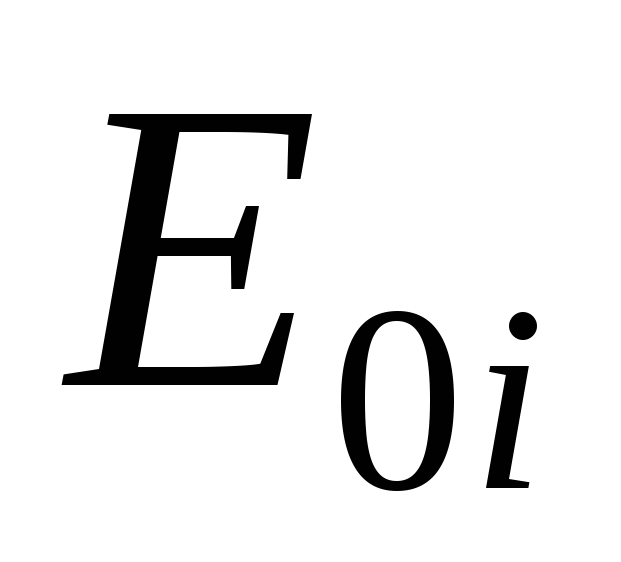 — модуль общей деформации грунта
элементарного слоя;
— модуль общей деформации грунта
элементарного слоя;
 — безразмерный коэффициент, принимаемый
для всех грунтов равным 0,8;
— безразмерный коэффициент, принимаемый
для всех грунтов равным 0,8;
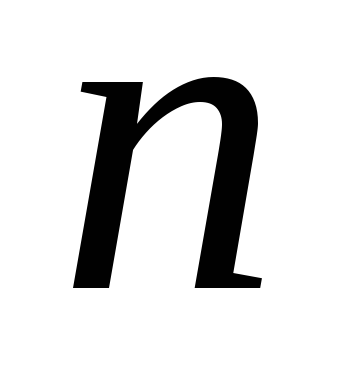 — число элементарных слоев грунта, на
которое разделена по глубине активная
зона сжатия.
— число элементарных слоев грунта, на
которое разделена по глубине активная
зона сжатия.
Напряжения 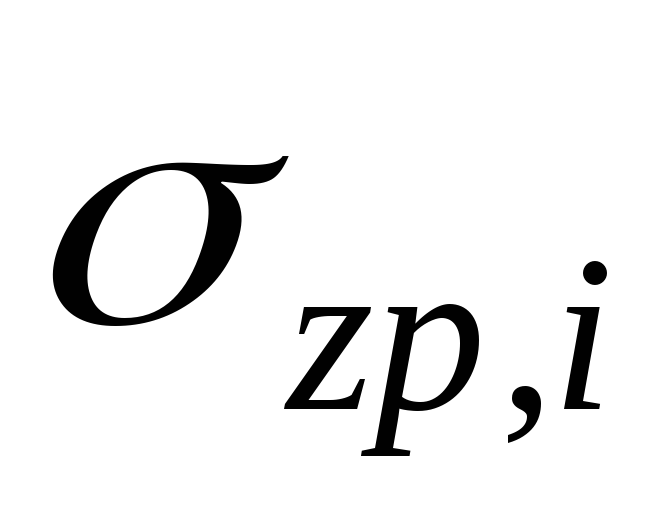 вычисляются по формуле:
вычисляются по формуле:
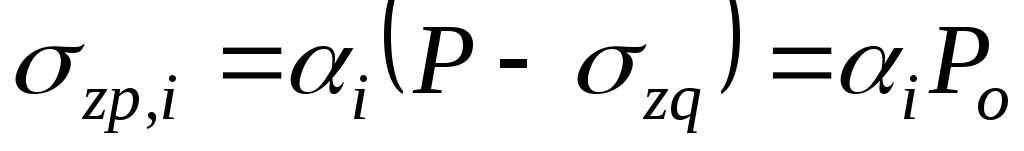 ,
,
где 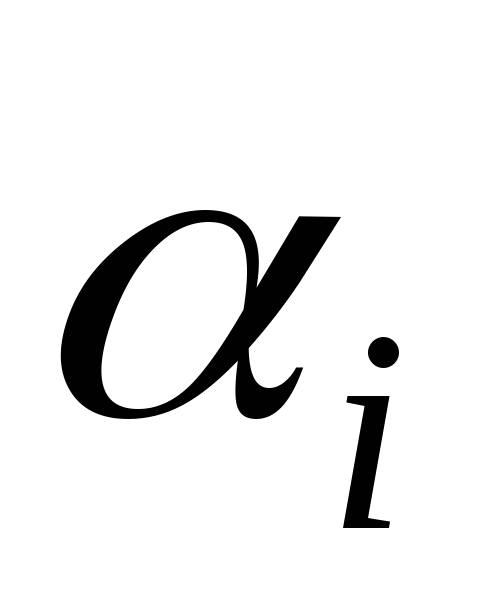 — коэффициент рассеивания напряжений,
принимаемый для полосообразной нагрузки
(
— коэффициент рассеивания напряжений,
принимаемый для полосообразной нагрузки
(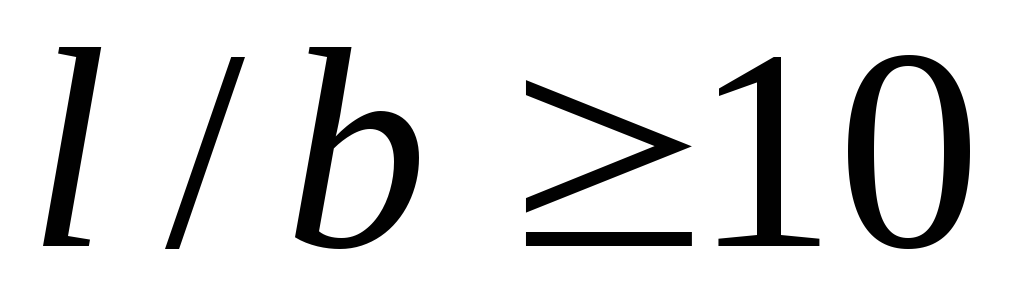 )
по таблице в зависимости от относительной
глубины
)
по таблице в зависимости от относительной
глубины ;
;
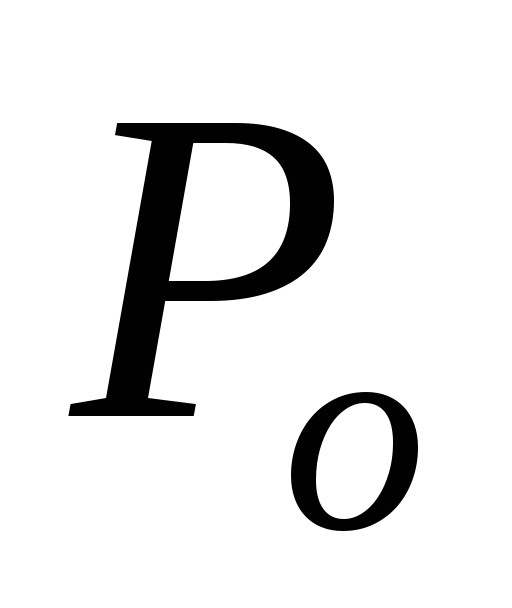 — давление на подошве полосы нагружения,
вызывающее осадку;
— давление на подошве полосы нагружения,
вызывающее осадку;
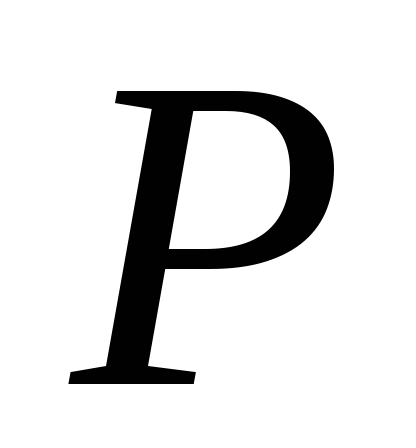 — интенсивность полосообразной нагрузки;
— интенсивность полосообразной нагрузки;
 — природное давление в грунте на уровне
подошвы полосы нагружения.
— природное давление в грунте на уровне
подошвы полосы нагружения.
Значения
коэффициента  приведены в табл.2.1 приложения 2 настоящих
методических указаний.
приведены в табл.2.1 приложения 2 настоящих
методических указаний.
Глубина
активной зоны сжатия 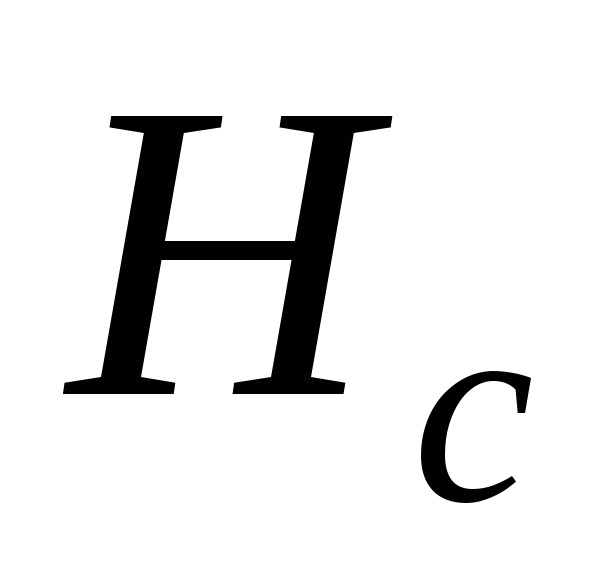 соответствует такой глубине, ниже
которой деформациями грунтовой толщи
можно пренебречь. В общем случае её
рекомендуют принимать на глубине, где
напряжение
соответствует такой глубине, ниже
которой деформациями грунтовой толщи
можно пренебречь. В общем случае её
рекомендуют принимать на глубине, где
напряжение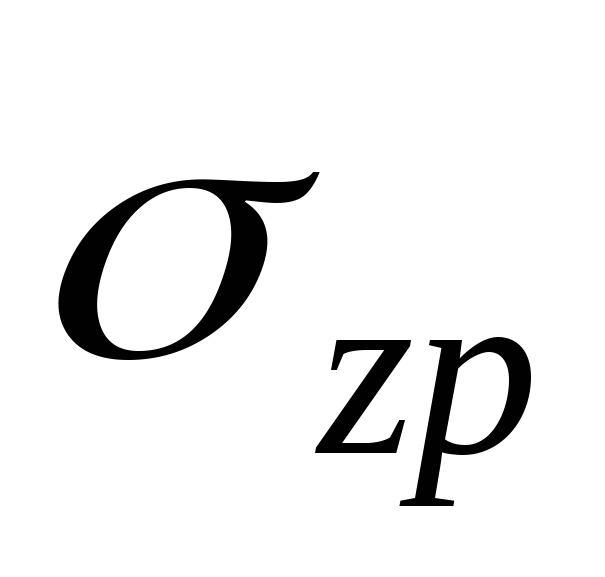 составляет 0,2 величины природного
давления.
составляет 0,2 величины природного
давления.
При построении расчетной схемы следует принимать масштаб расстояний 1:50, масштаб напряжений 0,05 МПа в 1 см.
Пример.
Дано: 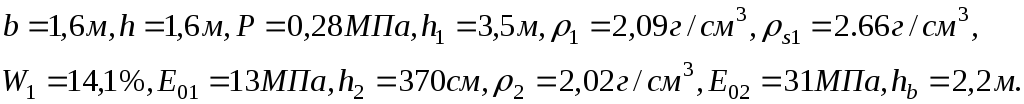
Решение:
Вычисляем ординаты эпюр природного
давления  и вспомогательной эпюры
и вспомогательной эпюры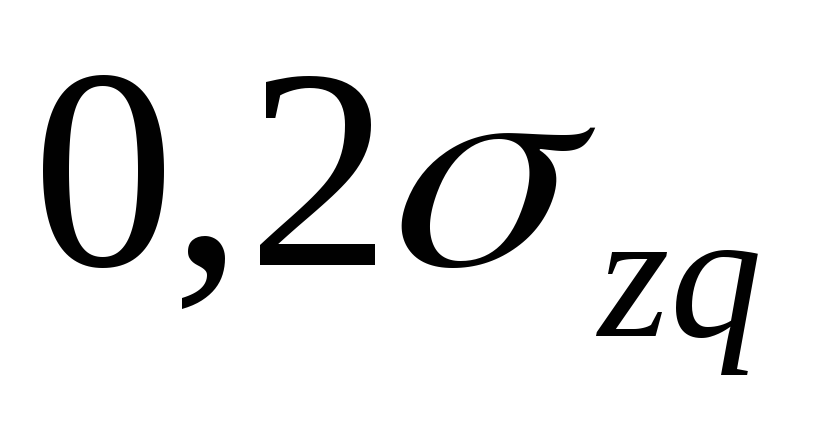 :
:
на уровне поверхности земли
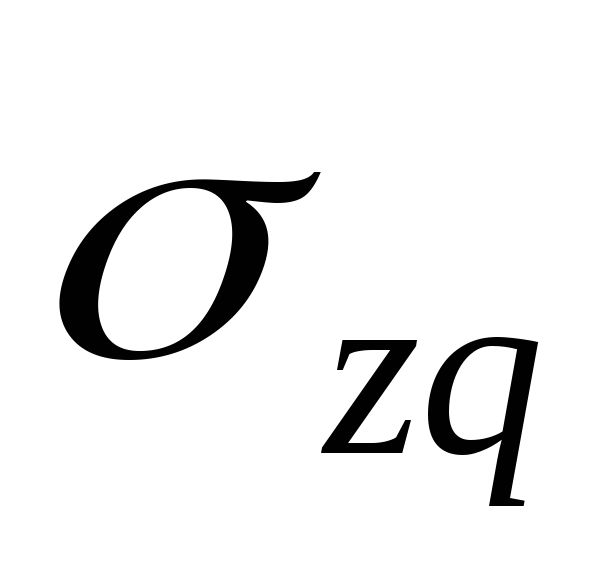 =0
=0 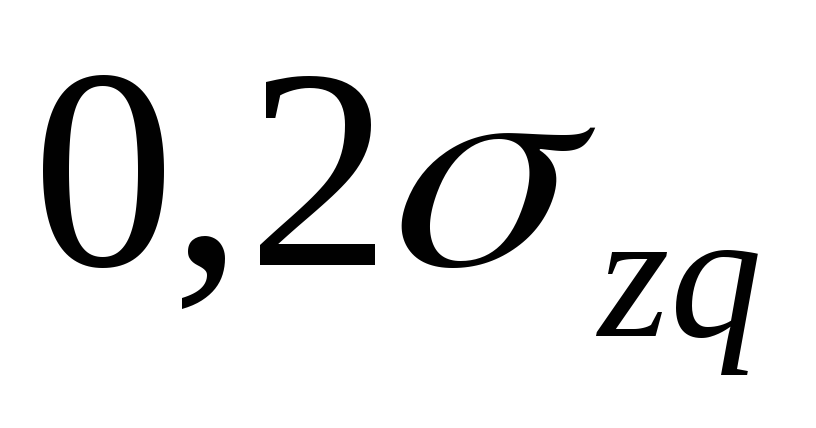 =0
=0
на уровне грунтовых вод
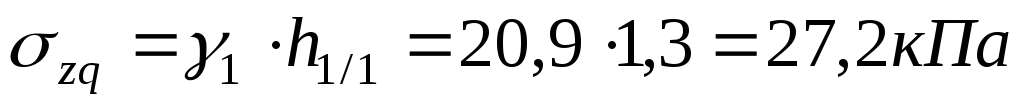
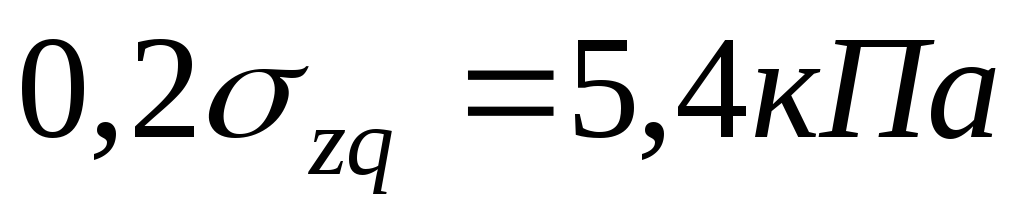
на уровне подошвы фундамента с учетом взвешивающего действия воды
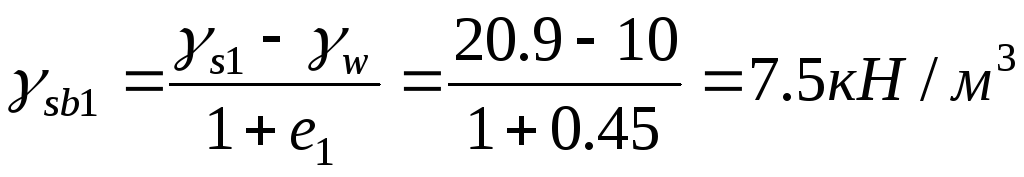 ,
,
где  .
.
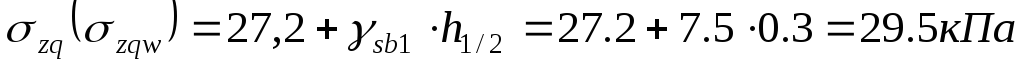 ,
, 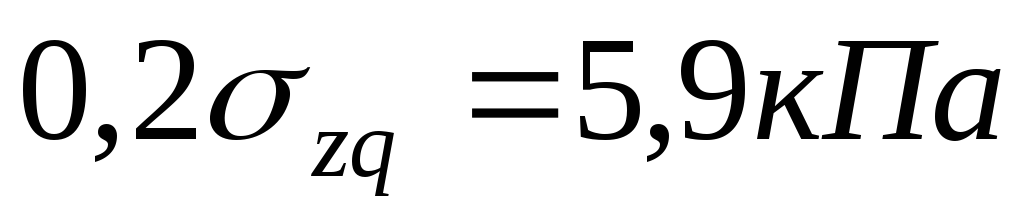 .
.
на границе первого слоя
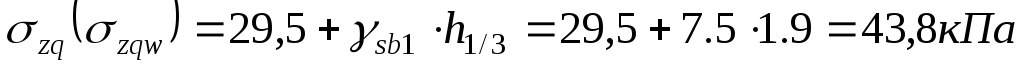 ,
, 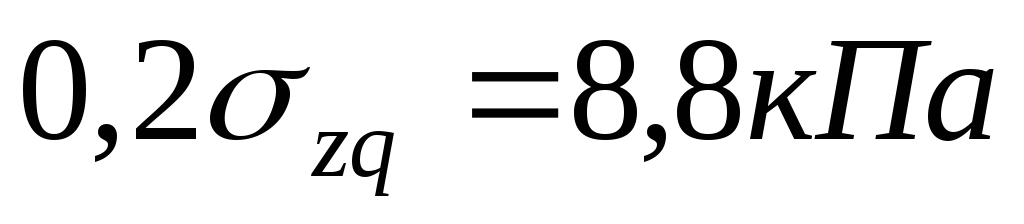 .
.
Так как во втором слое залегает водонепроницаемая глина, к вертикальному напряжению на кровлю глины добавляется гидростатическое давление столба воды, находящейся над глиной:
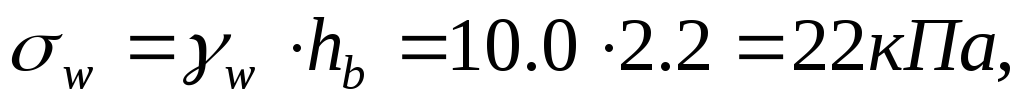
тогда полное вертикальное напряжение, действующее на кровлю глины:
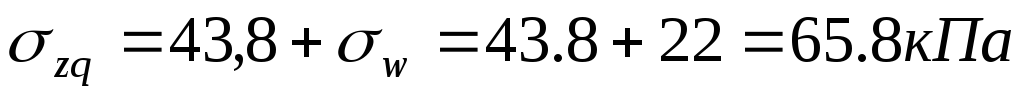 ,
, 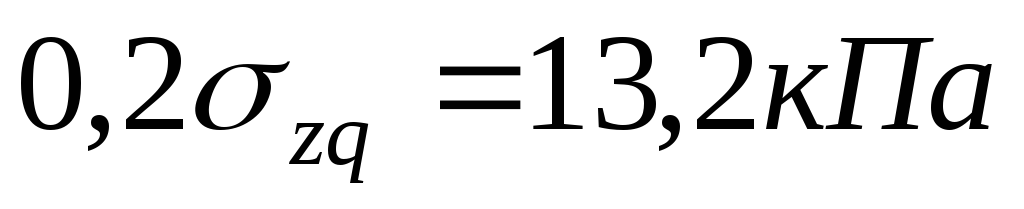 .
.
на границе второго слоя
 ,
, 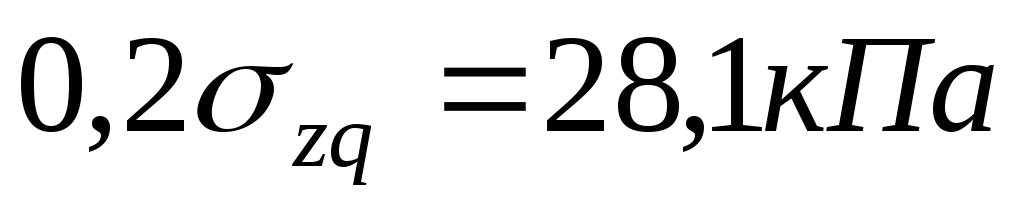 .
.
Определяем давление на подошве полосы нагружения, вызывающее осадку:
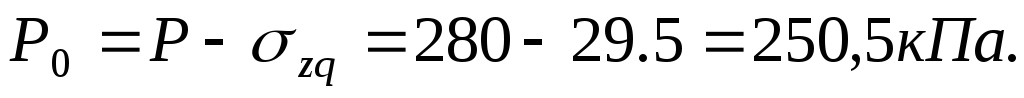
Разбиваем толщу грунта под подошвой полосы нагружения на элементарные слои:

Для удобства расчета осадки все вычисления ведем в табличной форме.
Наименование грунта |
|
|
|
|
|
|
песок | 0,00 0,64 0,64 0,62 | 0,00 0,64 1,28 1,90 | 0,0 0,8 1,6 2,4 | 1,000 0,881 0,642 0,477 | 250,5 220,7 160,8 119,5 | 13000 |
глина | 0,64 0,64 0,64 0,64 0,64 0,50 | 2,54 3,18 3,82 4,46 5,10 5,60 | 3,2 4,0 4,8 5,6 6,4 7,0 | 0,374 0,306 0,258 0,223 0,196 0,180 | 93,7 76,7 64,6 55,9 49,1 45,1 | 31000 |
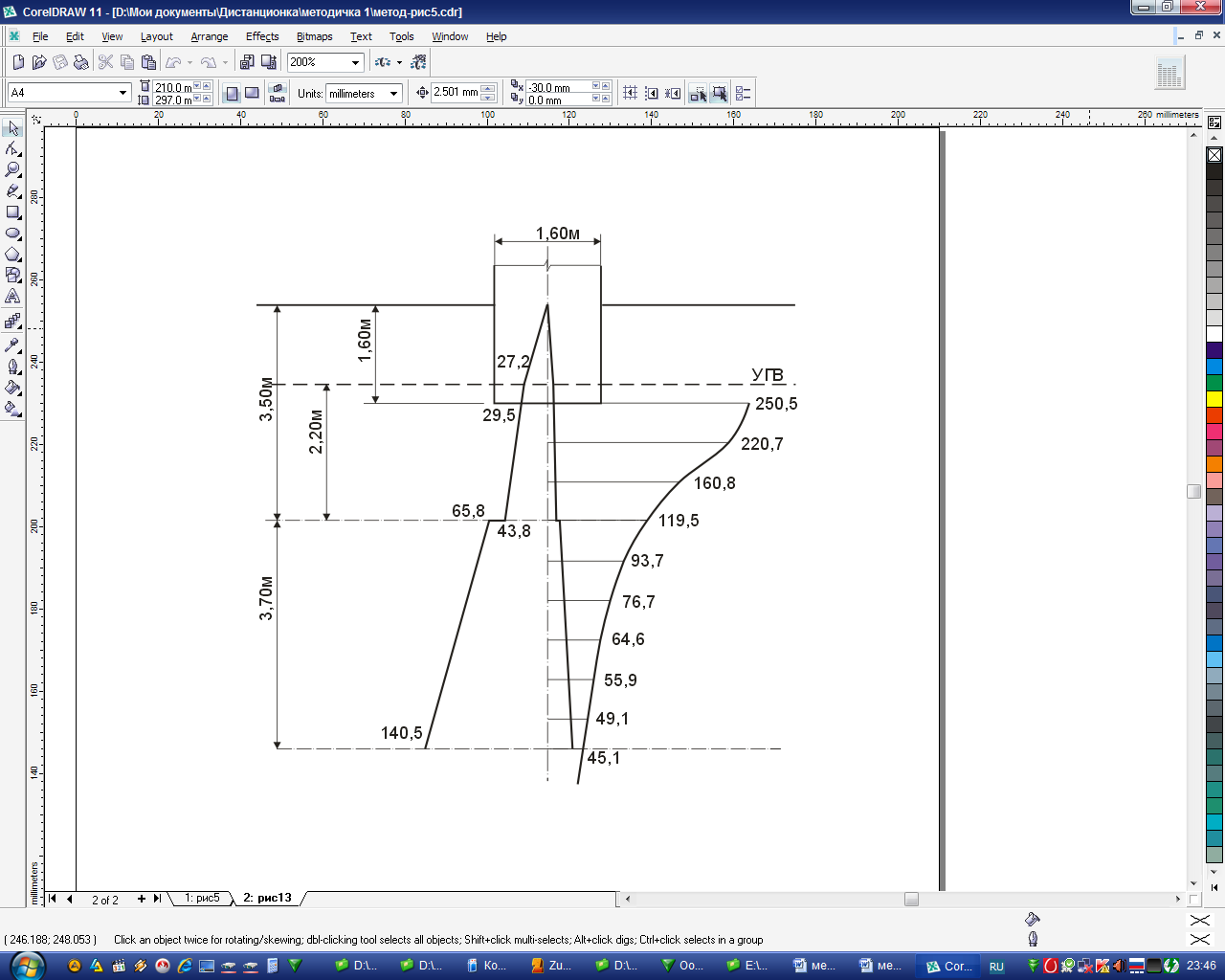
Рис.3.5. Расчетная схема к определению осадки методом послойного суммирования
В
нашем случае напряжения на уровне
подошвы второго слоя 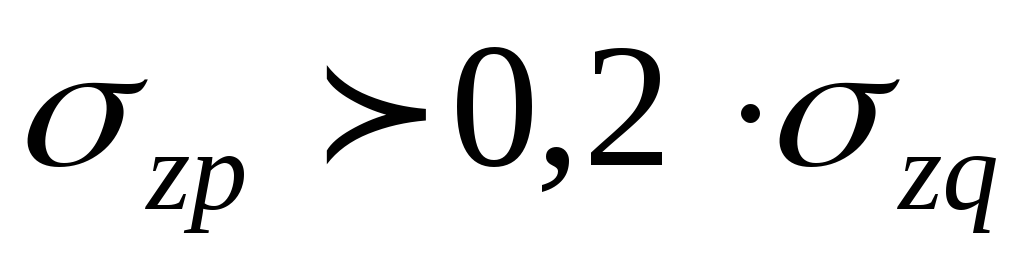 .
.
Определяем величину осадки в пределах двух слоев:
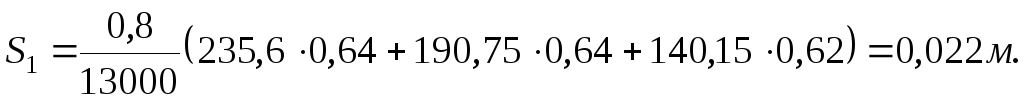

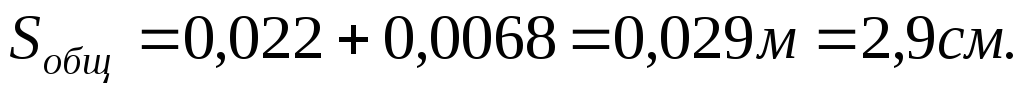 < Su = 8 см.
Условие выполняется, следовательно,
фундамент запроектирован правильно.
< Su = 8 см.
Условие выполняется, следовательно,
фундамент запроектирован правильно.
Давление грунтов на сооружения. Устойчивость оснований сооружений.
Понятие о давлении грунта и его зависимости от смещения сооружения.
При решении практических задач из общего напряженного состояния массива грунта обычно выделяют в отдельную задачу определение усилий, передающихся грунтом на вертикальные или наклонные грани сооружения. Типичными конструкциями, для которых существенно важна оценка давления грунта Е, являются различного рода подпорные стены (рис. 6.1, а), стены подвальных помещений (рис. 6.1, б), устои мостов (рис. 6.1, в), гидротехнические сооружения (рис. 6.1, г), ограждения котлованов, перемычки и др.
Рис. 6.1. Давление грунта на различные сооружения.
1 — область («призма») обрушения грунта;
2 — область («призма») выпора грунта.
Как убедительно показали эксперименты и натурные наблюдения, давление грунта Е на сооружение существенно зависит от направления, величины и характера смещений вертикальных или наклонных контактных граней сооружения, по которым происходит взаимодействие с грунтовым массивом.
Рассмотрим влияние смещений на примере простейшей подпорной стены (рис. 6.2). В случае уверенно неподвижной стены (рис. 6.2, в) деформации грунта происходят без бокового расширения и поэтому при действии только собственного веса грунта можно принять σx = ξσz = ξγгрz, где ξ — коэффициент бокового давления грунта (см. раздел 3.3, ф-ла 3.23). При этом суммарное боковое давление на единицу длины стены (в направлении, перпендикулярном плоскости хz) определится как E0 = ξγгрh2/2. Давление E0 принято называть давлением покоя, поскольку величина коэффициента ξ в E0 отвечает случаю отсутствия боковых смещений грунта.
Рис. 6.2. Зависимость давления грунта от величины и направления
горизонтального смещения стенки или сооружения.
Под действием давления грунта могут возникать смещения U сооружения в сторону от грунта засыпки (на рис. 6.2 приняты со знаком минус, т.е. U < 0). При этом в массиве грунта образуются поверхности скольжения, и постепенно формируется область обрушения, которую называют призмой (клином) обрушения (1 на рис. 6.2, б). Возникающие в смещающемся грунте силы сопротивления сдвигу приводят к уменьшению давления грунта, которое при величине смещения Ua сооружения, определяемой формированием призмы обрушения, достигает предельного (минимального) значения, называемого активным давлением или распором Еa (рис. 6.2, а). Как показали эксперименты, для достижения Еa необходимы весьма незначительные величины смещения стенки от грунта (Ua ≥ (0,0002 … 0,002)h, где h — высота стенки в м).
Нередко в результате действия внешних сил перемещения сооружения происходят в сторону грунта. Это может проявляться в сооружениях, воспринимающих большие горизонтальные нагрузки, например, в случае устоя арочного моста (рис. 6.1, в), гидротехнических сооружений (рис. 6.1, г) в результате давления воды верхнего бьефа.
При перемещении U стены на грунт (рис. 6.2, г) постепенно формируется призма выпора грунта (2 на рис. 6.2, г) и возникают силы сопротивления сдвигу, препятствующие выпору. В результате по грани стены возникает все увеличивающаяся реакция грунта, которая в момент формирования призмы выпора достигает максимальной величины, называемой пассивным давлением или отпором грунта Еп (рис. 6.2, а). Для развития и создания пассивного давления грунта требуется большое перемещение Uп стены на грунт, значительно (на 1 … 2 порядка) превышающее Ua. Это вызвано, в частности, уплотнением грунта за стенкой. При действии внешней нагрузки, принудительно смещающей стенку на грунт, грунт вначале уплотняется и только затем начинает формироваться поверхность скольжения — выпора грунта [12].
Таким образом, под активным давлением понимается предельное давление грунта засыпки на стенку (сооружение) в условиях, когда стенка смещается от засыпки (за счет деформации основания от давления засыпки) и грунт за стенкой перешел в состояние предельного равновесия. Пассивное давление — это предельное значение реакции (реактивного давления) при принудительном смещении стенки на грунт в условиях, когда грунт за стенкой переходит в состояние предельного равновесия (в пределах призмы выпора). Подчеркнем, что по отношению к сооружению активное давление — это активная, а пассивное давление — реактивная сила. Активное давление грунта может явиться одной из причин потери устойчивости сооружения или стенки (сдвига, крена и опрокидывания).
Для определения активного и пассивного давлений на массивные сооружения большой жесткости в проектной практике применяются обычно приближенные решения, основанные на представлениях теории предельного равновесия (ТПР – см. раздел 3.1), рассматриваемые ниже.
Статическое и динамическое давление грунтов и расчёт подпорных стенок
Предисловие 3
Глава 1. Общие положения строительной механики грунтов 5
§ 1. Грунты и их свойства 5
§ 2. Трение и сцепление в грунтах, углы откоса 9
§ 3. Поведение грунтов под нагрузкой 16
Глава 2. Теория статического давления грунтов на подпорные стенки 22
§ 4. О давлении грунтов в предельном состоянии 22
§ 5. Активное давление сыпучего тела по Кулону 26
§ 6. Графическое определение наибольшего активного давления 30
§ 7. Графоаналитическое определение максимального активного давления 34
§ 8. Построение Понселе. Частные случаи давления при плоской поверхности 38
§ 9. Аналитическое выражение активного давления для плоской поверхности сыпучего тела 44
§ 10. О направлении давления грунта 46
§ 11. О точке приложения равнодействующего давления 49
§ 12. Случаи ломаной грани стенки и ломаной поверхности сыпучего тела 52
§ 13. Давление грунта при действии распределённых нагрузок; давление разнородных грунтов 57
§ 14. Давление грунта при наличии сосредоточенных сил на поверхности 65
§ 15. Влияние воды на давление грунтов 70
§ 16. Давление грунта с учётом капиллярного действия воды 76
§ 17. О пассивном давлении сыпучего тела 83
§ 18. Учёт сцепления при определении бокового давления грунта 86
§ 19. Определение давления грунта от горизонтальных сил, приложенных на поверхности 94
§ 20. Краткий исторический обзор теорий давления грунтов 97
§ 21. Применение теории напряжённого состояния к определению давления при ломаной линии сползании 104
Глава 3. Расчёт массивных подпорных стенок на прочность, жёсткость основания и устойчивость 109
§ 22. Общие положения по расчёту подпорной стенки на прочность 109
§ 23. Построение многоугольника давлений и определение эксцентриситетов 112
§ 24. Определение напряжений в сечениях стенки и поверка прочности 116
§ 25. Осадки грунтового основания подпорных стенок 122
§ 26. Метод коэффициента постели при определении осадок 124
§ 27. Устойчивость подпорных стенок 129
§ 28. Поверка стенки на устойчивость при сдвиге по криволинейной поверхности скольжения 136
§ 29. Поверка заглублённой в грунт стенки на сдвиг при наличии отпора 140
Глава 4. Теория определения бокового давления грунта на основе уравнений деформаций 144
§ 30. Область применения теории Кулона. Пассивное давление в зависимости от перемещения стенки 144
§ 31. Исходные данные по зависимости между сопротивлением сдвигу и перемещением стенки 150
§ 32. Влияние вида перемещения стенки на величину и точку приложения давления грунта 154
§ 33. Определение действительного давления сыпучего тела с учётом сдвига стенки и клина сползания 156
§ 34. Реактивные сопротивления при сдвиге и повороте стенки 163
§ 35. Теория определения действительного давления грунта при сдвиге и повороте стенки 166
Глава 5. Теория определения динамического бокового давления грунта при наличии различных видов смещения стенки 166
§ 36. Введение 169
§ 37. Динамические характеристики работы грунта 172
§ 38. Динамическое давление грунта на подпорную стенку при её сдвиге 176
§ 39. Силы инерции при сдвиге и повороте стенки 186
§ 40. Дифференциальные уравнения движения стенки как системы с двумя степенями свободы и приближенное решение задачи 191
§ 41. Решение задачи о динамическом давлении грунта интегрированием системы дифференциальных уравнений 199
§ 42. Решение задачи о динамическом давлении грунта для случая нежёсткой грунтовой среды 206
§ 43. Дифференциальные уравнения для расчёта стенки как системы с тремя степенями свободы. Коэффициенты жесткости основания 213
§ 44. Решение задачи о динамическом давлении грунта для наклонной грани стенки как системы с тремя степенями свободы 223
Глава 6. Динамические напряжения в грунтовой среде при ударе по основанию. Точка приложения бокового давления 233
§ 45. Определение динамических напряжений в грунтовой призме способом приведённой массы 233
§ 46. Определение перемещений и напряжений в грунте при действии динамической нагрузки 241
§ 47. Точка приложения динамического бокового давления грунта 246
§ 48. Динамическая осадка фундаментов, несущих балочный ростверк при ударе 248
Глава 7. Теория и расчёт тонких стенок и свай на действие горизонтальных сил 260
§ 49. Расчёт абсолютно жёсткой тонкой стенки на горизонтальную силу по способу предельного состояния 260
§ 50. Расчёт абсолютно жёсткой тонкой стенки по способу ломаной эпюры давлений грунта 267
§ 51. Динамическая задача о колебании высокой опоры 272
§ 52. Расчёт абсолютно жёсткой стенки как балки на упругом основании 275
§ 53. Расчёт сваи как гибкой длинной балки на упругом основании 279
§ 54. Расчёт гибкой сваи с учётом влияния продольной сжимающей силы 285
Приложение 288
Литература 290
Оглавление 293

 ,м
,м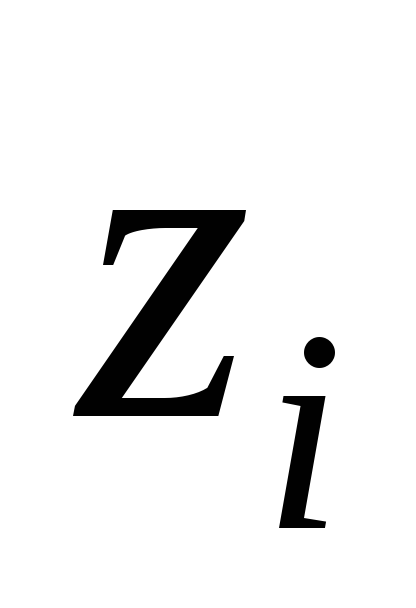 ,
м
,
м
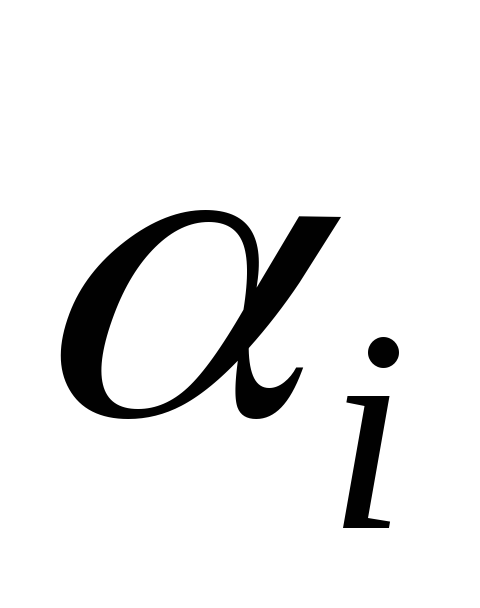
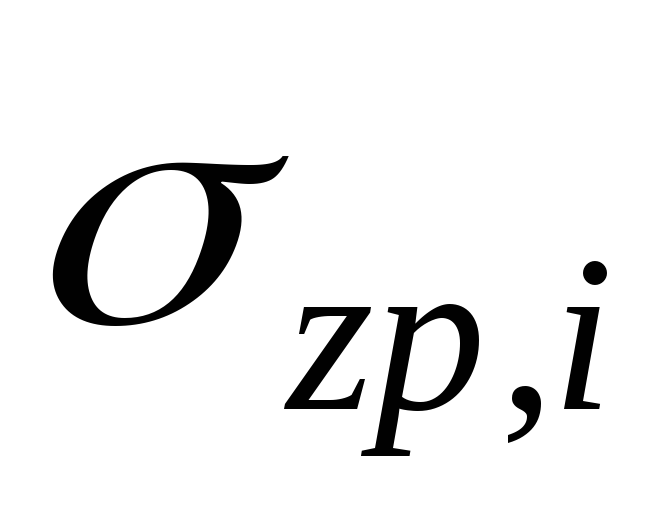 ,кПа
,кПа ,
кПа
,
кПа